深入浅出Python量化交易实战--第5章 因子基本原理和用法

第5章　因子基本原理和用法

在第4章中，小瓦学会了使用量化交易平台获取更多的数据，并 且通过一些基础的财务指标进行了最简单的选股。在这个过程中，小 瓦不仅学会了如何从量化交易平台获取数据，还掌握了一些基础财务 知识。而且，小瓦还提出了一个有趣的想法：把股价的涨幅和主力资 金的流入／流出这两种数据组合成一个“因子”，用于预测股价次日的 涨跌。为什么说这个想法有趣呢？看完本章，相信读者朋友们就会明 白了。

本章的主要内容如下。

1. 因子分析的基本原理。
2. 因子分析的简单方法。
3. 因子的作用。
4. 如何使用因子选股。

5.1　“瓦氏因子”

因子投资是时下投资界非常热门的方向。甚至有人戏称因子研究 是“诺贝尔奖收割机”：1990年，哈里·马科维茨凭借“均值——方差分 析”获得了诺贝尔经济学奖；同年，威廉·夏普凭借他的“资本资产定价 模型”也摘得诺贝尔奖桂冠；到了2013年，提出Fama-French三因子模型 的尤金·法马也获得了诺贝尔经济学奖，同时，Fama-French三因子模型 也被认定为金融领域的重大成就之一。 那么，到底什么是“因子”呢？不妨用小瓦的实验来说明一下。在这 个实验中，小瓦计算了一个非常简单，甚至有点儿“幼稚”的因子，但这 也能够说明因子分析的基本原理了。为了纪念这一“伟大创举”，我们将 这个因子命名为“瓦氏因子”。

import pandas as pd
import numpy as np
# 导入jqdata的所有工具包
from jqdata import *


# pd.set_option()是输出控制显示的设置
pd.set_option('expand_frame_repr', False)  # True就是可以换行显示。设置成False的时候不允许换行
pd.set_option('display.max_columns', None)  # 显示所有列
pd.set_option('display.max_rows', None)  # 显示所有行
pd.set_option('colheader_justify', 'centre')  # 显示居中

5.1.1 获取主力资金流向数据

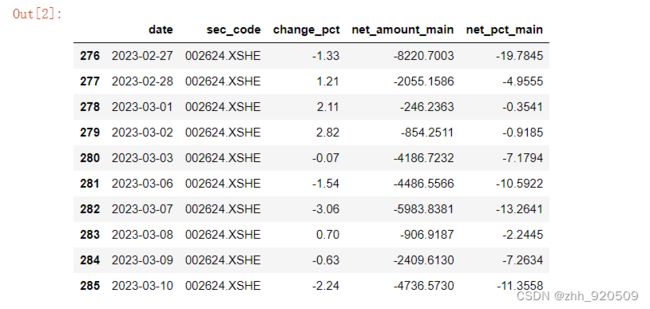
使用get_money_flow函数获取了股票的资金流入／流出数据， 并且发现了一个可能存在的规律——某日该股票价格上涨，且主力资金净流入的话，次日股价可能上涨；否则股价下跌。 为了进行实验，这里再次获取股票的资金流入／流出数据。为了便于后面训练模型，这次我们把数据的时间范围扩大至2年。

 

df = get_money_flow('002624.XSHE', 
                    fields = ['date',
                              # 股票代码
                              'sec_code', 
                              # 涨跌幅
                              'change_pct', 
                              # 主力金额，包括超大单和大单
                              'net_amount_main', 
                              # 主力成交额占总成交额的比例
                              'net_pct_main'
                             ], 
                    # 设置起始日期
                    start_date = '2022-01-01', 
                    end_date = '2023-03-10'
                   )
df.tail(10)

 

5.1.2　简易特征工程

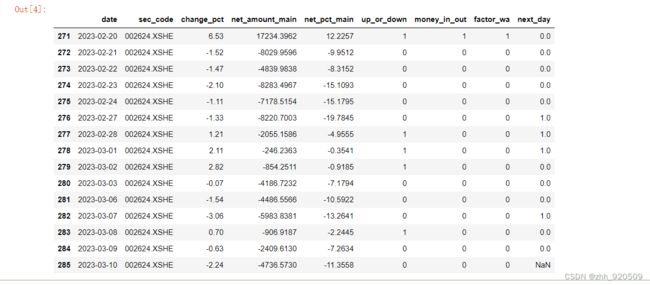
下面我们给原始的数据增加两个新的字段，其中一个是up_or_down，用来表示当日股价是上涨还是下跌。 如果change_pct（涨幅）这个字段为正数，说明股价上涨，则up_or_down用1来表示，反之，用0表示，代表当日股价下跌。 类似地，我们用money_in_out字段表示主力资金净流入还是净流出。如果net_amount_main大于0，说明主力资金净流入， 则在money_in_out字段用1表示；反之说明主力资金净流出，money_in_out字段用0表示。

# 增加一个字段，记录股价上涨还是下跌
# 如果上涨则以1标记，否则以0标记
df['up_or_down'] = np.where(df['change_pct']>0, 1, 0)
# 增加一个字段，记录主力资金净流入还是流出
# 如果净流入，标记为1；否则标记为0
df['money_in_out'] = np.where(df['net_amount_main']>0, 1, 0)

df.tail(10)

 

5.1.3　“瓦氏因子”的计算

现在我们有了两个新的特征，能够体现股价的涨跌和主力资金的流入／流出情况，下面就可以用这两个新的特征来计算“瓦氏因子”了。 咱们先说说思路。如果我们把两个特征相乘，则当股价上涨，且主力资金净流入时，因子值就是up_or_down乘以money_in_out， 也就是1×1，结果是1；而其他情况，“瓦氏因子”的数值都为0。例如，股价下跌但主力资金净流入，“瓦氏因子”为0×1，结果为0。 同时，为了后面便于模型训练，我们还要做一个标签（即次日股票上涨还是下跌），存储在next_day字段中。

 

# 瓦氏因子就是'up_or_down'乘以'money_in_out'，得出因子值
df['factor_wa'] = df['up_or_down'] * df['money_in_out']
# 把次日涨跌作为预测标签存储到‘next_day’字段
df['next_day'] = df['up_or_down'].shift(-1)
df.tail(15)

 

5.1.4　用添加“瓦氏因子”的数据训练模型

既然我们已经有了一个“瓦氏因子”，不妨来试试在数据集中加入这个因子之后，模型的预测准确率是否能够提高。 下面我们就导入机器学习工具，并且准备训练模型用的数据集。

# 导入KNN算法
from sklearn.neighbors import KNeighborsClassifier
# 导入数据集拆分工具
from sklearn.model_selection import train_test_split

dataset = df.drop(['date',
                   'sec_code',
                   'up_or_down',
                   'money_in_out'],
                  axis=1)
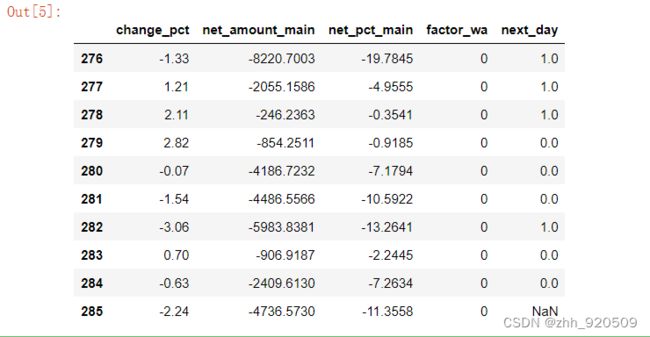
dataset.tail(10)

 

 因为最后一天是没有next_day数据的（因为对于最后一天来说，下一个交易日还没到来），所以我们要去掉最后一行数据； 同时，把除标签以外的特征赋值给X，把标签赋值给y；再使用数据集拆分工具，将X和y分别拆分成训练集和验证集。

# 将'next_day'以外的字段，作为数据集的特征
X = dataset.drop(['next_day'],axis=1)[:-1]
# 将'next_day'作为数据集的标签
y = dataset['next_day'][:-1]
# 将数据集拆分为训练集和验证集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 28)

 为了便于复现，上面的代码指定random_state为28。这样，即使多次运行代码，输出结果也不会不同。 下面就可以训练模型，使用KNN分类算法。

# 创建KNN分类器，n_neighbors参数依然取95
knn = KNeighborsClassifier(n_neighbors=95)
# 使用训练集训练模型
knn.fit(X_train, y_train)
# 输出训练集中模型准确率
print(knn.score(X_train, y_train))
# 输出验证集中模型准确率
print(knn.score(X_test, y_test))

 

 

5.2 股票不知道怎么选？因子来帮忙

5.2.1 确定股票池

不论能不能 赚到钱，至少要保证资金的安全——因此选择“沪深300”成分股作为选 股的“股票池”，并结合量化选股因子，找到其中财务状况最好、发展前 景最好的企业的股票，作为未来的投资标的。

5.2.2 获取沪深两市的全部指数

在“聚宽”平台上，我们可以通过get_all_securities函数，查询到全部指数的代码、中文名称、简称、起止日期等。

# 获取沪深两市的全部指数
indices = get_all_securities(types=['index'])
print(indices.head(10))
print(indices.tail())

 

5.2.3 获取股票的市值因子

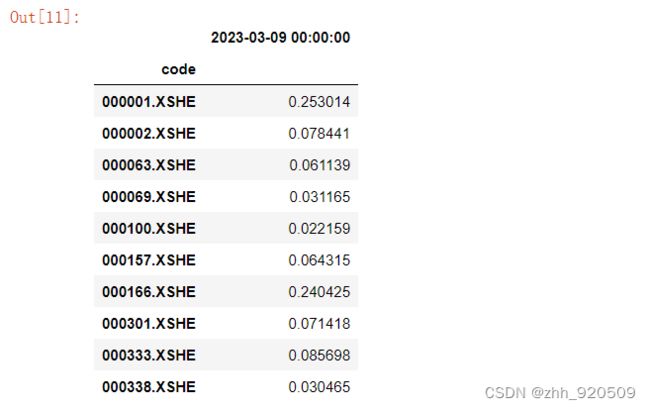
如前文所说，我们推荐小瓦使用“沪深300”成分股作为选股的股票池。下面我们就来获取沪深300成分股的数据。 获取这些股票的市值数据

from jqfactor import *
# 获取股票的市值因子
factor_mc = get_factor_values(securities=get_index_stocks('000300.XSHG'),
                              factors=['market_cap'], end_date='2023-03-09', count=1)['market_cap']
factor_mc.T.head(10)

 

5.2.4获取股票的现金流因子

除了关心股票的整体市值之外，我们还想了解企业的现金流与股价 的对比情况，也就是“市现率”这个指标的情况。毕竟经济大环境不好的 话，充足的现金流才是保证企业生存发展的前提。因此，我们来获取一下股票市现率的倒数（因为市现率越小越好，因此其倒数越大越好）。

 

# 获取股票的现金流因子
factor_cfp = get_factor_values(securities=get_index_stocks('000300.XSHG'),
                               factors=['cash_flow_to_price_ratio'],
                               end_date='2023-03-09',
                               count =1)['cash_flow_to_price_ratio']
# 查看因子值
factor_cfp.T.head(10)

 

5.2.5 获取股票的净利率因子

既然我们了解了企业的现金流情况，那么接下来我们就要看看这些 企业究竟是盈利还是亏损。如果盈利，那么净利润率又是多少呢？相信 小瓦也非常想知道答案。我们就继续来查询这些股票的净利润率数据。

 

# 获取股票的净利率因子
factor_npr = get_factor_values(securities=get_index_stocks('000300.XSHG'),
                               factors=['net_profit_ratio'],
                               end_date='2023-03-09',
                               count =1)['net_profit_ratio']
# 查看因子值
factor_npr.T.head(10)

 

5.2.6 获取股票的净利润增长率因子

对企业来说，盈利固然重要，比盈利更重要的是，能够持续不断地 创造更多的利润。也就是说，企业需要有良好的成长性。衡量成长性的 一个重要指标就是净利润的增长率。下面我们就来获取“沪深300”成分股的净利润增长率数据

# 获取股票的净利润增长率因子
factor_npgr = get_factor_values(securities=get_index_stocks('000300.XSHG'),
                               factors=['net_profit_growth_rate'],
                               end_date='2023-03-09',
                               count =1)['net_profit_growth_rate']
# 查看因子值
factor_npgr.T.head(10)

 

5.3 把诸多因子“打个包”

到此，我们已经有了4个因子——市值、市现率倒数、净利润率和 净利润增长率。看到这里，读者朋友们可能也会和小瓦问同样的问题： 既然有4个因子，那我们究竟应该采用哪个指标来进行选股呢？是选择 市值更大的？还是现金流更好的？抑或是选择净利润高、净利润增长率高的呢？如果让人来做出选择，这个题目确实有难度。我们不妨让机器 帮我们梳理一下答案。

5.3.1 将4个因子存入一个DataFrame

这里的思路是，把4个因子进行降维处理，用一个主成分表示4个因 子，这样我们就可以按照主成分的数值高低来选择股票了。

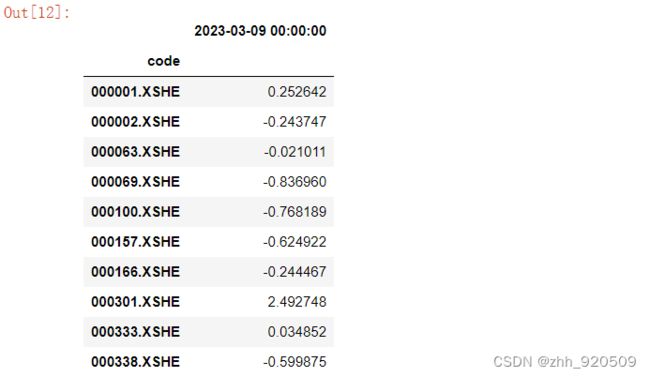
# 新建一个DataFrame，和市值数据保持同样的序号
factors = pd.DataFrame(index = factor_mc.T.index)
factors['mc'] = factor_mc.T['2023-03-09 00:00:00']
factors['cfp'] = factor_cfp.T['2023-03-09 00:00:00']
factors['npr'] = factor_npr.T['2023-03-09 00:00:00']
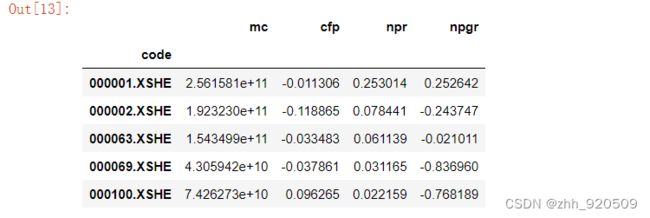
factors['npgr'] = factor_npgr.T['2023-03-09 00:00:00']
factors.head()

5.3.2 使用PCA提取主成分

下面我们就开始进行主成分分析的过程。说到主成分分析，小瓦第 一个想到的就是主成分分析（Principle Component Analysis，PCA）算 法。PCA是一种无监督学习算法，在数据科学领域，常用于进行样本特 征的降维处理。关于PCA的原理，本书不打算展开详细介绍，只要大家 明白，这个算法就是通过方差来确定样本各个特征的重要性，并且给它 们分配不同的权重（重要性越高的特征，分配的权重也越高），并根据 权重，将高维数据降到低维的过程。如果读者朋友对详细的PCA原理感 兴趣，自行在网上进行搜索即可。 为了便于计算，数据中不能有空值，所以要用下面的代码进行处 理。

 

#为了计算，先把数据中的空值去掉
factors = factors.dropna()
#检查是否还有空值
factors.isnull().sum()

 接下来，我们使用PCA来对4个因子进行降维处理。考虑到各个因 子的量纲差异比较大，这里我们先进行数据缩放的步骤，再进行主成分 分析。

# 因为各因子数值的量纲差异较大
# 需要做一点简单的缩放处理
from sklearn.preprocessing import StandardScaler
# 导入scikit-learn中的PCA工具
from sklearn.decomposition import PCA
# 创建StandardScaler实例，会将数据量纲压缩到同一个区间中
scaler = StandardScaler()
# 使用StandardScaler缩放原始的因子值
factors_scl = scaler.fit_transform(factors)
# 接下来使用PCA，提取主成分数量指定为1
pca =PCA(n_components=1)
# 使用缩放后的数据进行拟合
pca.fit(factors_scl)
# 查看PCA给各因子分配的权重
pca.components_

5.3.3 找到主成分数值最高的股票

我们可以让小瓦尝试将PCA提取的主成分添加到数据表里，并找到 主成分数值最高的几只股票。

#在factors数据表中添加一个pca字段
#存储提取出来的主成分
factors['pca'] = pca.transform(factors_scl)
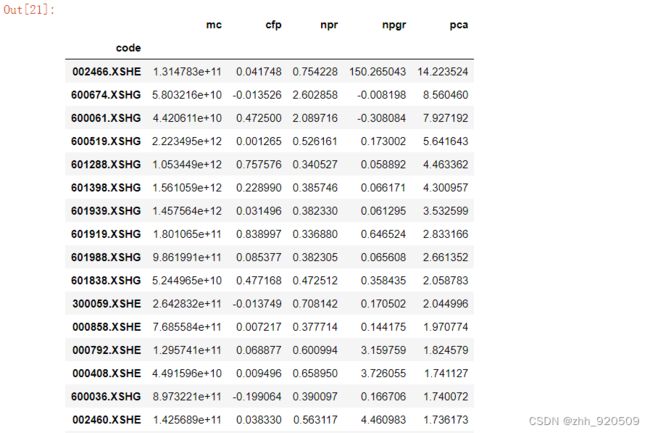
#看一下主成分数值最高的5只股票
factors.sort_values(by='pca', ascending = False).head(20)

 

注意：这里展示的只是一个简单的思路。实际上，关于因子选股 的思路和方法有很多种。读者朋友们可以发挥自己的聪明才智，通过 使用不同的因子与算法，找到最适合自己的投资组合。

5.4　小结

在本章中，我们通过一个简单的因子计算过程，让小瓦理解了因子 分析的基本原理，也介绍了因子的作用——帮助我们选股和找到买卖时 机。同时，我们从“聚宽”平台获取了“沪深300”成分股的若干个基本面 因子，并且用无监督学习的方法，对多个因子进行了主成分分析。通过 主成分的数值高低，我们选出了一些基本面数据看起来不错的股票。到 这里，小瓦的量化交易之路还算是比较顺利。在第6章中，我们就来进 一步研究因子，并掌握因子分析的主要指标和收益情况。读者朋友们也 不要放松，让我们一鼓作气向着财富狂奔吧。