全国大学生FPGA创新设计竞赛:FPGA—相位干涉仪测向算法
1.项目总体及相位干涉仪测向概述
根据调查发现,对于一些特定信号的快速精准定位一直是世界性难题。不仅仅是对某些会给国家和社会带来严重安全威胁的非法信号的定位跟踪,还可能是对紧急情况下的搜求信号的精确定位。
相位干涉仪测向算法顾名思义是利用无线电信号到达测向天线的相位信息来进行测向的,这种算法不受信号强度衰减的影响,与振幅法相比具有更高的测向精度,但是一维单基线相位干涉仪测向算法可能会产生对称模糊,会具有多个定位角度。
本项目信号源的产生采用自研的以Artix7核心板为主控并集成AD9361的硬件平台实现,由DDS模块产生深度为4096,位宽为12位的可调节频率信号,利用2FSK技术发射I\Q路特定信号。
2.系统整体架构
我们使用自研硬件平台产生2.4GHZ频率的信号,用AD9361对信号进行采样、混频工作,将得到的下变频信号作为输入信号输入到信号处理端。信号处理端的框图如图2-2所示,我们使用Artix-7 50T硬件平台作为输入信号的处理核心,系统的FPGA侧实现无源定位的算法,求解出来波信号的角度,将其输出结果经过运算处理以后再通过串口转发至PC端上位机中显示。
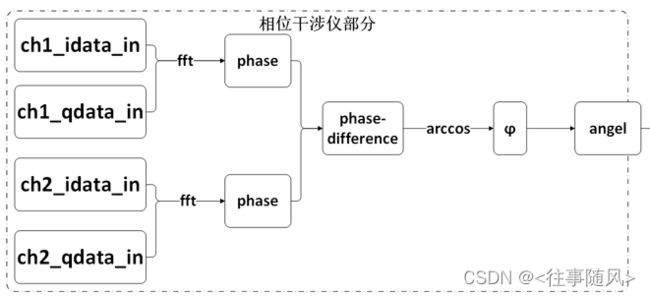
3.系统基本原理介绍
相位干涉仪测向的信号处理部分的算法主要原理依据一维干涉仪的测向原理。当目标信号辐射至天线阵列时,因为天线阵列各阵元间有一定的距离,所以同一基线上各阵元接收信号间存在一定的时差 。时差可以在一定的条件下变换为相差,相位干涉仪测向算法可以利用各基线上阵元接收信号间的相差完成对目标的测向,一维单基线相位干涉仪测向原理如下图所示。

单基线干涉仪测向有两个阵元天线,间距是d。来波与天线中轴线之间的角度(即俯仰角)是 ,那么可以求到信号到达两天线的路程差为:

设辐射源信号的波长是 λ \lambda λ,则两天线间的相位差是 φ \varphi φ ,表示如下式:
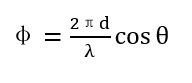
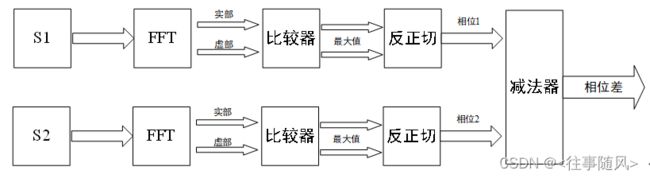
4.算法原理详解
4.1.整理实现流程
系统将前端输出的两路信号序列S1和S2输入到FPGA中,之后使能FFT模块,将两路序列进行快速傅里叶变换后得到两路序列的频域图,将得到的频域图通过比较器筛选出两路信号虚部和实部的最大值,再将其经过反正切算法分别得到两路信号的相位值,最后经过减法器将两路信号的相位值做差得到相位差。下图为算法流程图。
4.2.FFT测量模块
首先,假设两路接收信号为S_i ( n ) \left(n\right) (n)(i=1,2)在经过FFT之后得到离散频谱S_i\left(k\right),其频率所在的点的谱线的实部和虚部分别包含了信号相位的余弦信息和正弦信息,基于快速傅里叶变换的FFT测量法正是利用这两项信息分别求得两路被测信号的相位值,最后相减得到相位差 。FFT是离散傅里叶变换(DFT)的快速算法,根据DFT的原理
S i ( k ) = D F T [ S i ( n ) ] = ∑ n = 0 N − 1 s ( n ) e x p ( − j 2 π N n ) S_i\left(k\right)=DFT\left[S_i\left(n\right)\right]=\sum_{n=0}^{N-1}s\left(n\right)\mathrm{exp} \left(\mathrm{-j}\frac{\mathrm{2\pi}}{\mathrm{N}}\mathrm{n} \right) Si(k)=DFT[Si(n)]=∑n=0N−1s(n)exp(−jN2πn)= = R e [ S i ( k ) ] + I m [ S i ( k ) ] =Re\left[S_i\left(k\right)\right]+Im\left[S_i\left(k\right)\right] =Re[Si(k)]+Im[Si(k)]
式中:i=1,2,k=0,1,2,…,N-1;N为FFT长度。能量最大的谱线即为被测信号频率所在的谱线,即:
k 0 = f 0 N f S k_0=\frac{f_0N}{f_S} k0=fSf0N
式中f_s为采样频率;f_0为被测信号频率;N为FFT长度。所以,接收信号S_1,S_2的相位 φ 1 , φ 2 \varphi_1,\varphi_2 φ1,φ2可以表示为:
φ i = a r c t a n ( I m [ S i ( k 0 ) / R e [ S i ( k 0 ) ] ) \varphi_i=arctan(Im[Si(k0)/Re[Si(k0)]) φi=arctan(Im[Si(k0)/Re[Si(k0)])
式中:i=1,2;k_0可通过在FFT频谱上搜索最大值方法确定 。最后将两路被测信号的相位差相减即可得到相位差 Δ φ \Delta\varphi Δφ:
Δ φ = a r c t a n I m [ S 1 ( k 0 ) ] / R e [ S 1 ( k 0 ) ] − a r c t a n I m [ S 2 ( k 0 ) ] / R e [ S 2 ( k 0 ) ] \Delta\varphi=arctanIm[S1(k0)]/Re[S1(k0)]-arctanIm[S2(k0)]/Re[S2(k0)] Δφ=arctanIm[S1(k0)]/Re[S1(k0)]−arctanIm[S2(k0)]/Re[S2(k0)]
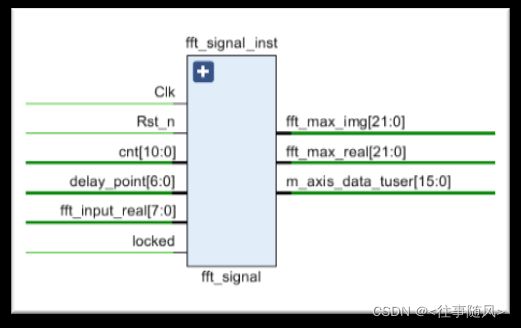
4.3.FFT模块设计
在IP核的配置中,我们设置输入信号点数为8192,输入数据位宽为8位,模式配置为非实时模式。之后,在模块内部设计一个比较器,将傅里叶变换之后的最大值输出到下一级模块中。整个模块的RTL视图如下图所示。
4.4.鉴相器模块设计
此模块中,我们设置CORDIC为Arctan模式,设置其输入数据的位宽为22位,输出数据位宽为14位,该模块负责接受上一级FFT模块传输出的实部和虚部的最大值 ,通过内部的时序,使得整个模块正常运行。整个模块的RTL视图如下图所示。

4.5 相位干涉法来波角度解算部分
由单基线干涉仪测向的原理我们可以知道相位差与来波俯仰角之间的数学关系为:

所以可以反解得到:
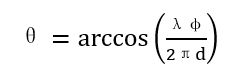
此处 λ \lambda λ和2πd均为已知量,所以当得到相位差之后便可以解算出来波俯仰角 。在这个过程中,需要用到反余弦算法。
4.6.CORDIC算法基本原理
在直角坐标系中,假设有一向量 ( x , y ) \left(x,y\right) (x,y),按逆时针方向旋转 φ \varphi φ度得到向量 ( x 1 , y 1 ) \left(x_1,y_1\right) (x1,y1),则两向量的代数关系为:

如果让旋转的角度\varphi满足条件: t a n ( φ ) = ( ± 2 ) tan\left(\varphi\right)=\left(\pm2\right) tan(φ)=(±2)-j,则式(2.1)中的乘法操作就可以转换为移位操作,从而很容易在FPGA中实现 。下图所示是直角坐标下的向量旋转示意图。若需要旋转的角度 θ \theta θ,那么就可以通过n次旋转一系列预定角度 α i \alpha\ i α i来完成。

θ = ∑ i = 0 n − 1 d i a i , d i ∈ − 1 , 1 \theta=\sum_{i=0}^{n-1}d_ia_i,d_i\in{-1,1} θ=∑i=0n−1diai,di∈−1,1
上式中,d_i表示每次旋转的方向为\alpha\ i。由于每次旋转都为预定角度值,所以cos\alpha i为常数,而n次旋转中每次迭代的处理可表示为:
一般情况下,当旋转的次数足够大时K_i一般为常数。由于在实现时,可在最终的计算结果中再乘以这一常数,所以,可以去掉式(2.22)(2.23)中的K_i,这样,迭代方程就仅含移位和加法运算,从而大大的简化了FPGA的实现复杂性。由于还需要一个方程决定d_i的符号,引入变量Z_i表示每次旋转预定角度的累加值。

这样,CORDIC算法的迭代方程可表示为:


其最终
可见,经过上述处理就可将输入相位z_0转换为标准的正弦和余弦信号。
4.6.FPGA内反余弦算法实现
首先假设 θ = a r c t a n ( x ) \theta=\mathrm{arctan}\left(x\right) θ=arctan(x)把该三角形看作一个直角边分别为1和 的直角三角形,斜边为\sqrt{1+x^2};所以
θ = a r c s i n ( x 1 + x 2 ) = a r c c o s ( 1 + x 2 x ) \theta=arcsin\left(\frac{x}{\sqrt{1+x^2}}\right)=arccos\left(\frac{\sqrt{1+x^2}}{x}\right) θ=arcsin(1+x2x)=arccos(x1+x2)
由反余弦算法的推导我们可以得出如下的数学关系:
a r c c o s θ = a r c t a n 1 − θ 2 θ \mathrm{arccos\theta=arctan}\frac{\sqrt{1-\theta^2}}{\theta} arccosθ=arctanθ1−θ2
根据该关系式对arctan的输入数据进行简单运算处理就可以得到arccos的运算电路。即该arccos模块的设计由一个乘法器,一个减法器,一个平方根计算的IP核和arctan模块构成,整个模块的RTL视图如下:
5.完成情况及性能参数
5.1.matlab仿真部分
利用matlab模拟了两通道包含i路、q路信号相位差为90°的采集信号,每通道信号经过FFT变换得出各通道信号的实部信号与虚部信号,其中第一通道采集信号的时域、频域图如下图所示。
第二通道采集信号的时域、频域图如下图所示。

通过FFT变换以后,解算出通道一信号的各点的幅度值后,求解出了最大的幅度值为4096,并找到了最大幅度值所对应的点的下标为8065。

按照该点下标便可求出对应的相位弧度制为0.4254 rad,转化为角度值为24.3750°。

第二通道中求解出了最大的幅度值为4096,并找到了最大幅度值所对应的频点的下标为8065。

第二通道按照该点下标求出对应的相位弧度制为0.7745 rad,转化为角度值为44.3750°。

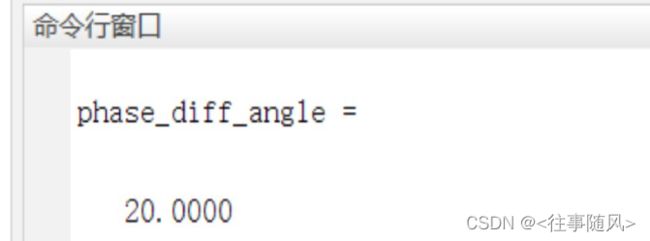
可得两信号相位差为20.0000°。
再根据来波结算公式,解算出来波角度为75.1°,作图如下

而计算出的真实位置角度为75.0965°。该系统误差仅为0.466%。

5.2.Vivado仿真部分
经过FFT变换以后,两路实部与虚部的结果如下图所示。

接收到输出的实部和虚部的最大值如下图所示。

利用上图求得的幅度最大值的频点信息,就可以得到该点的实部与虚部,如下图所示。知道这些信息以后,便可求解出相位。

比辐法部分解算出来波的位置模糊范围,并输出有效信号,相位干涉仪部分解算出来波的精确角度值,在比辐法部分解算出来的位置模糊范围内选取相位干涉仪部分解算出来的精确角度值即为最终来波的位置角度。如图3-19所示,得出最终的角度值为54°。

5.3.可扩展之处
(1)可以利用更精密的算法大幅提高测向精度;
(2)可通过增大采样率等方式提升定位精度;
(3)可完善测距功能。
本系统的设计对于我们团队来说都是一次全新的挑战,这是我们在FPGA学习道路上的首个尤为重要的比赛。我们三个在最初定题时是信心满满的,但到准备比赛过程中并不是一帆风顺。我们时常因为许多小问题而挫败,走了许多弯路,熬过许多夜晚。最困扰我们的是这学期面临着繁重的学业任务,在完成好比赛的同时又要兼顾学业,这成了我们最大的挑战。但是我们三个并未因此放弃,更多的是不懈努力,坚持到底。我们深知这个比赛的难度,也知道想要做好我们的工程就要对所做的工程进行全局分析以及清晰的阶段目标划分。我们从开始准备比赛到提交作品这段时间里,合理的根据各个成员的优劣势来分配工作,各个成员都努力的为这个比赛付出时间与精力。不论结果如何,我们三人在这次备赛中都更加深入地了解了 FPGA的性能以及使用方法。我们花了将近两个月的时间来仿真,调试我们的算法,在这个过程中,我们的FPGA编程能力得到了显著的提高,也进一步明白了团队合作的重要性,我们可以成功地完成这个作品,感觉是我们成长路上的一个大进步!
6.实际上板效果
最终效果是可以正确得出信号源的位置,由于此项目以后会运用到军工方面,在此不便于展示,请见谅。


