33.栈,队列练习题(王道2023数据结构第3章综合应用)
试题1(3.1.4节题3):
假设以 I 和 O 分别表示入栈和出栈操作。栈的初态和终态均为空,入栈和出栈的操作序列可表示为仅有 I 和 O 组成的序列,可以操作的序列为合法序列,否则称为非法序列。
(1)下面的序列哪些是合法的?
(A)IOIIOIOO (B)IOOIOIIO (C)IIIOIOIO (D)IIIOOIOO
(2)试写出一个算法,判定给定的操作序列是否合法。若合法则返回 True,否则返回 False(假定被判定的操作序列已存入一维数组中)。
解答:(1)AD合法,而BC不合法(注意C中最后栈的终态不为空,所以非法)。
(2)两步检验:检验中间是否有空栈还Pop的情况,检验最后栈是否为空
#include
#include
int main()
{
char a[10] = {'I','O','I','I','O','O','I','O','O','O'}; //待检测序列
int i = 0;
int j = 0;
while(a[i]!=NULL){
if(a[i]=='I')
j = j + 1;
else
j = j - 1;
if(j < 0){
printf("输入序列非法!");
return 0;
}
i = i + 1;
}
if(j==0){
printf("输入序列合法!");
return 1;
}
else{
printf("输入序列非法!");
return 0;
}
}
输出:
char a[10] = {'I','O','I','I','O','O','I','I','I','O'};
输入序列非法!
char a[10] = {'I','O','I','I','O','O','I','O','I','O'};
输入序列合法!试题2:(3.1.4节题4)
设单链表的表头指针为L,结点结构由data和next组成,其中data为字符型。设计算法判断该链表全部n个字符是否是中心对称的,如xyx,xyyx都是中心对称的。
这道题也不是很难,但是需要注意C语言中字符的输入输出怎么写。我在写这段代码的时候踩了一个大坑。参考:用scanf()输入单个字符时的注意点_wuyouzeng1121210068的博客-CSDN博客![]() https://blog.csdn.net/wuyouzeng1121210068/article/details/6935395加上空格后,回车符不在赋值给e,否则会报错。
https://blog.csdn.net/wuyouzeng1121210068/article/details/6935395加上空格后,回车符不在赋值给e,否则会报错。
#include
#include
#include
#define MAXSIZE 100
#define ElemType char
#define Status int
//单链表的数据结构
typedef struct LNode
{
ElemType data;
struct LNode *next;
}LNode, *LinkList;
//初始化
int InitList(LinkList &L)
{
L = (LNode *)malloc(sizeof(LNode));
L->next = NULL;
return 1;
}
//输出
void PrintList(LinkList L)
{
printf("当前单链表的所有元素:");
LNode *p;
p = L->next;
while (p != NULL)
{
printf("%c ", p->data);
p = p->next;
}
printf("\n");
}
//尾插法创建单链表
int Create(LinkList &L)
{
int n;
char e;
LNode *temp = L;//声明一个指针指向头结点,用于遍历链表
printf("请输入要输入元素的个数:");
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
LNode *a = (LNode*)malloc(sizeof(LNode));
printf("请输入第%d元素的值:", i);
scanf(" %c", &e); //%c必须有空格!!!,scanf必须要有取地址运算符&e
a->data = e;
temp->next = a;
a->next = NULL;
temp = temp->next;
}
return 1;
}
//插入元素
int InsertList(LNode *L, int i, ElemType e)
{
LNode *p = L;
int j = 0;
while (p && (j < i - 1)) //寻找要插入位置的前驱结点,让p指向它
{
p = p->next;
++j;
}
if (!p || j > i - 1) return 0; //插入位置非法,返回0
LNode *s = (LNode *)malloc(sizeof(LNode));
s->data = e; //创建一个新结点存放要插入的元素e
s->next = p->next; //把新结点的指针域指向p->next
p->next = s; //把p->next指向要插入的新结点
return 1;
}
//删除元素
int DeleteList(LNode *L, int i)
{
LNode *p = L;
int j = 0;
while (p->next && (j < i - 1)) //寻找要删除结点的前驱结点,让p指向它
{
p = p->next;
++j;
}
if (!p->next || j > i - 1) return 0; //删除位置非法,返回0
LNode *q;
q = p->next; //暂存删除结点,以便随后释放
p->next = q->next; //把p->next指向p->next->next,即q->next
free(q); //释放结点
return 1;
}
//按值查找元素
int LocateElem(LNode *L, ElemType e)
{
int i = 1;
LNode *p = L->next;
while (p&&p->data != e) //从第一个结点开始,依次向后遍历比较
{
p = p->next;
i++;
}
if(p) return i;
else return 0;
}
bool dc(LinkList L,int n){ //这里假设表长已知,本算法判断链表是否中心对称
LNode *p;
int i = 0;
char s[n / 2]; //建立栈
p = L->next;
for (i = 0; i < n / 2;i++){
s[i] = p->data;
p = p->next;
}
i = i - 1; //退出循环时还要加1,这里再减回去就是n/2
if(n % 2== 1){ //注意:表长是奇数时,需要越过中间结点
//例如表长是5,则n/2=2,退出for循环时i=3,p指针指向第3个元素
//但是第3个元素和第3个元素必定相等,所以p指针移动到4号,比较2和4即可
p = p->next;
}
while(p!=NULL&&s[i] == p->data){
i = i - 1;
p = p->next;
}
if(i==-1){
printf("此链表是中心对称的");
return 1;
}
else{
printf("此链表不是中心对称的");
return 0;
}
}
int main(){
LinkList L;
InitList(L);
Create(L);
PrintList(L);
dc(L,5);
/*
InsertList(L, 4, 'w');
PrintList(L);
DeleteList(L, 3);
PrintList(L);
printf("%d\n",LocateElem(L, 's'));
*/
return 0;
} 输出:
当前单链表的所有元素:a b d b a
此链表是中心对称的
当前单链表的所有元素:a b v f d
此链表不是中心对称的试题3:(3.1.4节题5)
设有两个栈S1,S2都采用顺序栈方式,并共享一个存储区[0...Maxsize-1],为了尽量利用空间,减少溢出可能,可采用栈顶相向,迎面增长的存储方式,试设计S1,S2的入栈和出栈算法。
此题考的是共享栈,这里复习一下C语言中switch()选择语句的写法:
#include
#include
#include
#define MAXSIZE 10
#define ElemType int
#define Status int
//共享栈的数据结构
typedef struct
{
ElemType data[MAXSIZE];
int top[2]; //两个栈的栈顶指针
}Stack;
//栈的初始化
int InitStack(Stack &a){
a.top[0] = -1;
a.top[1] = MAXSIZE; //初始两个指针都指向栈底
return 0;
}
//打印栈的元素
void PrintStack(Stack a){
if(a.top[0]>=0){
for (int i = 0; i <= a.top[0];i++){
printf("[%d]", a.data[i]);
}
}
if(a.top[1]-a.top[0]>1){
for (int i = a.top[0] + 1; i <= a.top[1]-1;i++){
printf("[NULL]");
}
}
if(a.top[1] <= MAXSIZE-1){
for (int i = a.top[1]; i <= MAXSIZE - 1;i++){
printf("[%d]", a.data[i]);
}
}
printf("\n");
}
//入栈,i为栈号,x表示入栈元素
int Push(Stack &a,int i,ElemType x){
if (i!=0 && i!=1){
printf("栈号出错!");
return 0;
}
else{
switch (i){
case 0:{
if(a.top[1]-a.top[0]==1){
printf("栈已满!");
return 0;
}
else{
a.top[0] = a.top[0] + 1;
a.data[a.top[0]] = x;
}
break; //不能缺少break语句,如果缺失,程序会把后面的case都执行。
}
case 1:{
if(a.top[1]-a.top[0]==1){
printf("栈已满!");
return 0;
}
else{
a.top[1] = a.top[1] - 1;
a.data[a.top[1]] = x;
}
break; //不能缺少break语句,如果缺失,程序会把后面的case都执行。
}
}
}
return 1;
}
//出栈
int Pop(Stack &a,int i,ElemType x){
if (i!=0 && i!=1){
printf("栈号出错!");
return 0;
}
else{
switch (i){
case 0:{
if(a.top[0]==-1){
printf("栈已空!");
return 0;
}
else{
x = a.data[a.top[0]];
a.top[0] = a.top[0] - 1;
return x;
}
break; //不能缺少break语句,如果缺失,程序会把后面的case都执行。
}
case 1:{
if(a.top[1]==MAXSIZE){
printf("栈已空!");
return 0;
}
else{
x = a.data[a.top[1]];
a.top[1] = a.top[1] + 1;
return x;
}
break; //不能缺少break语句,如果缺失,程序会把后面的case都执行。
}
}
}
}
int main(){
Stack a;
int x;
InitStack(a);
PrintStack(a);
Push(a, 0, 1);
Push(a, 1, 2);
Push(a, 1, 3);
PrintStack(a); //元素入栈之后打印
Pop(a, 0, x);
Pop(a, 1, x);
Pop(a, 0, x);
PrintStack(a); //元素出栈后再打印
return 0;
}
输出:
[NULL][NULL][NULL][NULL][NULL][NULL][NULL][NULL][NULL][NULL]
[1][NULL][NULL][NULL][NULL][NULL][NULL][NULL][3][2]
栈已空!
[NULL][NULL][NULL][NULL][NULL][NULL][NULL][NULL][NULL][2]试题4:(3.2.5节题1)
若希望队列中的元素都能得到利用,需设置一个标志域tag,并以tag为0或1来区分头指针front和尾指针rear相同时的队列状态是空还是满,试编写此结构的入队和出队算法。
本题中我们重写循环队列(采用数组)的有关算法:
#include
#include
#include
#define MAXSIZE 6
#define ElemType int
#define Status int
//循环队列的数据结构
typedef struct Queue
{
ElemType data[MAXSIZE];
int front, rear; //头尾指针,队头指针指向第一个元素,队尾指针指向队尾元素的下一个元素
int tag;
}Queue;
//初始化
int InitQueue(Queue &a)
{
a.front = 0;
a.rear = 0;
a.tag = 0; //初始队列是空
for (int i = 0; i < MAXSIZE;i++){
a.data[i] = 0;
}
return 1;
}
//打印输出
void PrintQueue(Queue a)
{
printf("当前队列所有元素:");
for (int i = 0; i < MAXSIZE;i++){
printf("[%d] ",a.data[i]);
}
printf("\n");
}
//插入队列
int Insert(Queue &a,ElemType x){
if(a.front == a.rear && a.tag == 1){
printf("当前队列已满!");
return 0;
}
else{
a.data[a.rear] = x;
a.tag = 1; //插入队列tag置1
a.rear = (a.rear + 1) % MAXSIZE;
return 1;
}
}
//删除队列
int Delete(Queue &a,ElemType x){
if(a.front == a.rear && a.tag == 0){
printf("当前队列已空!");
return 0;
}
else{
x = a.data[a.front];
a.data[a.front] = 0;
a.tag = 0; //删除队列tag置0
a.front = (a.front + 1) % MAXSIZE;
return x;
}
}
int main(){
Queue a;
int x;
InitQueue(a);
PrintQueue(a);
Insert(a, 1);
Insert(a, 2);
Insert(a, 3);
Insert(a, 4);
Delete(a, x);
PrintQueue(a);
Insert(a, 5);
Insert(a, 6);
Insert(a, 7);
Insert(a, 8);
PrintQueue(a);
return 0;
} 输出:
当前队列所有元素:[0] [0] [0] [0] [0] [0]
当前队列所有元素:[0] [2] [3] [4] [0] [0]
当前队列已满!
当前队列所有元素:[7] [2] [3] [4] [5] [6]试题5:(3.2.5节题2)
Q是一个队列,S是一个空栈,实现将队列中的元素逆置。
#include
#include
#include
#define MAXSIZE 6
#define ElemType int
#define Status int
//循环队列的数据结构
typedef struct Queue{
ElemType data[MAXSIZE];
int front, rear; //头尾指针,队头指针指向第一个元素,队尾指针指向队尾元素的下一个元素
int tag;
} Queue;
//栈的数据结构
typedef struct Sqstack{
ElemType data[MAXSIZE];
int top; //栈顶指针指向栈顶元素
} Sqstack;
//初始化
int InitQueue(Queue &a){
a.front = 0;
a.rear = 0;
a.tag = 0; //初始队列是空
for (int i = 0; i < MAXSIZE;i++){
a.data[i] = 0;
}
return 1;
}
int InitStack(Sqstack &a){
for (int i = 0; i < MAXSIZE;i++){
a.data[i] = 0;
}
a.top = -1;
return 1;
}
//打印输出
void PrintQueue(Queue a){
printf("当前队列所有元素:");
for (int i = 0; i < MAXSIZE;i++){
printf("[%d] ",a.data[i]);
}
printf("\n");
}
void PrintSqstack(Sqstack a){
printf("当前栈所有元素:");
for (int i = 0; i < MAXSIZE;i++){
printf("[%d] ",a.data[i]);
}
printf("\n");
}
//插入
int InsertQueue(Queue &a,ElemType x){
if(a.front == a.rear && a.tag == 1){
printf("当前队列已满!");
return 0;
}
else{
a.data[a.rear] = x;
a.tag = 1; //插入队列tag置1
a.rear = (a.rear + 1) % MAXSIZE;
return 1;
}
}
int InsertSqstack(Sqstack &a,ElemType x){
if(a.top == MAXSIZE-1){
printf("当前栈已满!");
return 0;
}
else{
a.top = a.top + 1;
a.data[a.top] = x;
return 1;
}
}
//删除
int DeleteQueue(Queue &a,ElemType x){
if(a.front == a.rear && a.tag == 0){
printf("当前队列已空!");
return 0;
}
else{
x = a.data[a.front];
a.data[a.front] = 0;
a.tag = 0; //删除队列tag置0
a.front = (a.front + 1) % MAXSIZE; //front指针+1
return x;
}
}
int DeleteSqstack(Sqstack &a,ElemType x){
if(a.top == -1){
printf("当前栈已空!");
return 0;
}
else{
x = a.data[a.top];
a.data[a.top] = 0;
a.top = a.top - 1;
return x;
}
}
int ReverseQueue(Queue &a){
Sqstack B;
InitStack(B);
int q = a.front; //记录一下起始地址位置
int x;
while(a.front!=a.rear || a.tag!=0){
InsertSqstack(B, DeleteQueue(a, x)); //出队列,入栈
}
a.front = q;
a.rear = q;
while(B.top!=-1){
InsertQueue(a, DeleteSqstack(B, x)); //入队列,出栈
}
return 0;
}
int main(){
Queue a;
int x;
InitQueue(a);
InsertQueue(a, 1);
InsertQueue(a, 2);
InsertQueue(a, 3);
InsertQueue(a, 4);
InsertQueue(a, 5);
InsertQueue(a, 6);
DeleteQueue(a, x);
InsertQueue(a, 7);
PrintQueue(a);
ReverseQueue(a);
PrintQueue(a);
return 0;
} 输出:
当前队列所有元素:[7] [2] [3] [4] [5] [6]
当前队列所有元素:[2] [7] [6] [5] [4] [3]
当前队列所有元素:[0] [2] [3] [4] [0] [0]
当前队列所有元素:[0] [4] [3] [2] [0] [0]
当前队列所有元素:[7] [0] [3] [4] [5] [6]
当前队列所有元素:[3] [0] [7] [6] [5] [4]试题6:(3.3.6节题1)利用栈进行括号匹配
这题原理十分简单,不多解释。
#include
#include
#include
#define MAXSIZE 10
#define ElemType char
#define Status int
//栈的数据结构
typedef struct Sqstack{
ElemType data[MAXSIZE];
int top; //栈顶指针指向栈顶元素
} Sqstack;
//初始化
int InitStack(Sqstack &a){
for (int i = 0; i < MAXSIZE;i++){
a.data[i] = '0';
}
a.top = -1;
return 1;
}
//插入
int InsertSqstack(Sqstack &a,ElemType x){
if(a.top == MAXSIZE-1){
printf("当前栈已满!");
return 0;
}
else{
a.top = a.top + 1;
a.data[a.top] = x;
return 1;
}
}
//删除
int DeleteSqstack(Sqstack &a){
ElemType x;
if(a.top == -1){
printf("当前栈已空!");
return 0;
}
else{
x = a.data[a.top];
a.data[a.top] = '0';
a.top = a.top - 1;
return x;
}
}
bool BracketsCheck(char str[]){
Sqstack a;
InitStack(a);
int i = 0;
char x = '0';
while (str[i]!='\0'){
switch (str[i]){
case '[':
InsertSqstack(a, str[i]);
break;
case '(':
InsertSqstack(a, str[i]);
break;
case '{':
InsertSqstack(a, str[i]);
break;
case '}':
x = DeleteSqstack(a);
if(x != '{'){
printf("输入括号序列不匹配!");
return false;
}
break;
case ']':
x = DeleteSqstack(a);
if(x != '['){
printf("输入括号序列不匹配!");
return false;
}
break;
case ')':
x = DeleteSqstack(a);
if(x != '('){
printf("输入括号序列不匹配!");
return false;
}
break;
default:
break;
}//switch
i = i + 1;
}//while
if(a.top != -1){
printf("输入括号序列不匹配!");
return false;
}
else{
printf("输入括号序列匹配!");
return true;
}
}
int main(){
printf("输入括号序列:");
char str[10];
gets(str);
BracketsCheck(str);
return 0;
} 输出:
输入括号序列:([]
输入括号序列不匹配!
输入括号序列:(())
输入括号序列匹配!试题7:(3.3.6节题2)铁路调度问题
所用栈的数据结构与上一题相同。
void TrainDispatch(char str[]){
Sqstack a;
InitStack(a);
char x;
int i = 0;
while(str[i]!='\0'){
if(str[i] == 'H'){
InsertSqstack(a, str[i]);
}
else{
printf("S");
}
i = i + 1;
}
while(a.top!=-1){
x = DeleteSqstack(a);
printf("%c", x);
}
}
int main(){
printf("输入火车序列:");
char str[10];
gets(str);
TrainDispatch(str);
return 0;
}输出:
输入火车序列:SHSHSH
SSSHHH试题8:(3.3.6节题3)利用栈实现递归函数的非递归计算: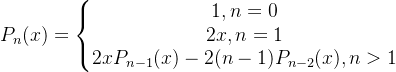
所用栈的数据结构同上。
double p(int n,double x){
Sqstack a;
InitStack(a);
double fv0 = 1;
double fv1 = 2 * x;
if(n==0)
return fv0;
else if(n==1)
return fv1;
else{
for (int i = 2; i <= n;i++){
a.top = a.top + 1;
}
for (int i = 2; i <= n; i++){
a.data[a.top] = 2 * x * fv1 - 2 * (i - 1) * fv0;
fv0 = fv1;
fv1 = a.data[a.top];
a.top = a.top - 1;
}
return fv1;
}
}
int main(){
printf("%f\n",p(2,3));
printf("%f\n",p(3,3));
return 0;
}输出:
34.000000
180.000000