二叉树题目：二叉树剪枝

题目

标题和出处

标题：二叉树剪枝

出处：814. 二叉树剪枝

难度

4 级

题目描述

要求

给定二叉树的根结点 $\text{root}$，返回移除了所有不包含 $\text{1}$ 的子树的原二叉树。

结点 $\text{node}$ 的子树为 $\text{node}$ 本身以及所有 $\text{node}$ 的后代。

示例

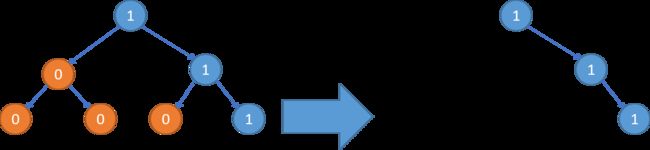
示例 1：

输入：$\text{root = [1,null,0,0,1]}$
输出：$\text{[1,null,0,null,1]}$
解释：
只有红色结点满足条件「所有不包含 $\text{1}$ 的子树」。右图为返回的答案。

示例 2：

输入：$\text{root = [1,0,1,0,0,0,1]}$
输出：$\text{[1,null,1,null,1]}$

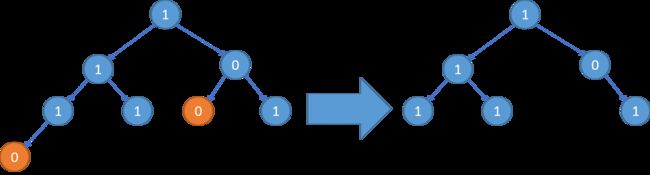
示例 3：

输入：$\text{root = [1,1,0,1,1,0,1,0]}$
输出：$\text{[1,1,0,1,1,null,1]}$

数据范围

• 树中结点数目在范围 $\text{[1, 200]}$ 内
• $\text{Node.val}$ 是 $\text{0}$ 或 $\text{1}$

解法

思路和算法

如果二叉树为空，则不需要执行剪枝操作，直接返回即可。

当二叉树不为空时，需要首先对二叉树的左子树和右子树执行剪枝操作，然后对当前二叉树执行剪枝操作。剪枝操作具体为，如果一个结点是叶结点且结点值为 $0$，则该结点被移除。注意在移除值为 $0$ 的叶结点之后，被移除的结点的父结点可能从非叶结点变成叶结点。

由于每个结点是否需要被移除和结点的子树有关，因此可以使用深度优先搜索实现。

整个过程是一个递归的过程。递归的终止条件是当前结点为空，或者当前结点是叶结点且结点值为 $0$，这两种情况都返回空二叉树。对于其余情况，递归地对左子树和右子树执行剪枝操作。

由于剪枝操作只会移除所有的值为 $0$ 的叶结点（包括从非叶节点变成叶结点的值为 $0$ 的结点），不会移除值为 $1$ 的结点，因此剪枝操作可以确保移除所有不包含 $1$ 的子树。

代码

class Solution {
    public TreeNode pruneTree(TreeNode root) {
        if (root == null) {
            return root;
        }
        root.left = pruneTree(root.left);
        root.right = pruneTree(root.right);
        if (root.left == null && root.right == null && root.val == 0) {
            root = null;
        }
        return root;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。每个结点都被访问一次。

• 空间复杂度：$O(n)$，其中 $n$ 是二叉树的结点数。空间复杂度主要是递归调用的栈空间，取决于二叉树的高度，最坏情况下二叉树的高度是 $O(n)$。