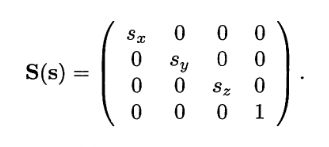ModelMatrix、ModelViewMatrix、ProjectionMatrix、NormalMatrix模型矩阵、模型视图矩阵、投影矩阵、正规矩阵详解

ModelMatrix、ModelViewMatrix、ProjectionMatrix、ModelMatrix模型矩阵、模型视图矩阵、投影矩阵、正规矩阵详解

1. 前言
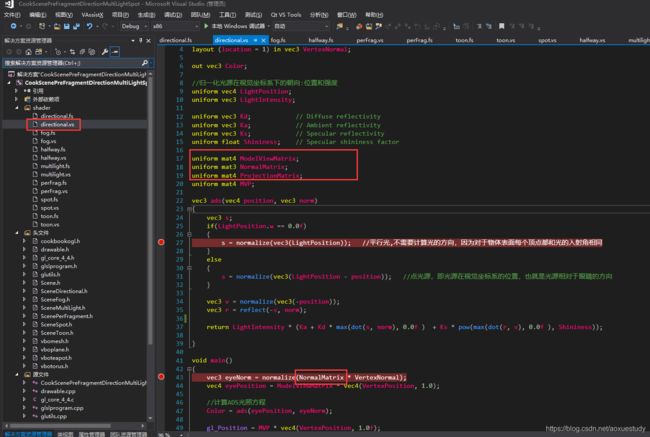
在openGL经常用到ModelMatrix、ModelViewMatrix、ProjectionMatrix、ModelMatrix（模型矩阵、模型视图矩阵、投影矩阵、正规矩阵）这几个矩阵，举个栗子：

效果：

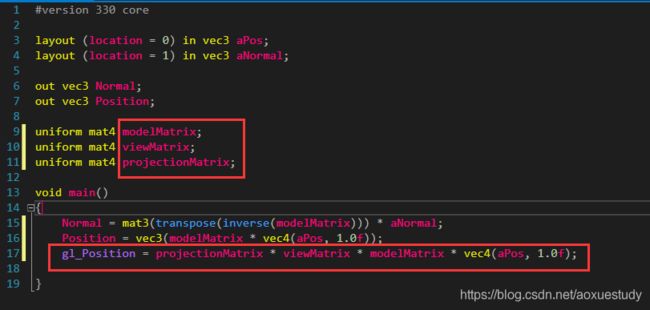
上面是一段顶点着色器的代码实现了：平行光光照效果，就用到了ModelMatrix、ModelViewMatrix、ProjectionMatrix、NormalMatrix这几个矩阵，除此之外，ADS（ambient，diffuse，specular环境光、漫反射、镜面高光）光照模型、聚光灯等都用到了这几个矩阵。可见这几个矩阵的重要性，我也很好奇，就这四个矩阵就模拟实现了现实生活中的光照。

2. 详细介绍

（1）基础
＊关于向量与点
点表示3维空间中的一个位置。向量表示一个方向，也就是两个点的差值，p1-p2。无论是说位置还是方向都需要事先说明它是在哪个坐标系中的。在进行坐标系转换时，某点的位置关乎此坐标系原点的位置，而方向则无关了。

OpenGL有6种坐标系
1，物体或模型坐标系(Object or model coordinates);
2，世界坐标系（World coordinates）
3，眼坐标或相机坐标（Eye (or Camera) coordinates)
4，裁剪坐标系（Clip coordinates）
5，标准设备坐标系（Normalized device coordinates）
6，屏幕坐标系（Window (or screen) coordinates）
7. 视口坐标系（ViewPort coordinates）
8. .纹理坐标系(Texture coordinates)
9. 齐次坐标（Homogeneous Coordinates）

OpenGL存在一种假想坐标系纹理坐标系，这个坐标系是不存在的，它其实是一系列变换矩阵的结果，比如它能使顶点从物体或模型坐标系变换到世界坐标系。
从object coordainates到world coordinates再到camera coordinate的变换，在OpenGL中统一称为model-view转换，初始化的时候，object coordinates和world coordinates还有camera coordinates坐标重合在原点，变换矩阵都为Identity,所以在OpenGL中用glLoadIdentity()初始化变换矩阵栈。model-view matix转换points,vectorsd到camera坐标系。

OpenGL 的重要功能之一就是将三维的世界坐标经过变换、投影等计算，最终算出它在显示设备上对应的位置，这个位置就称为设备坐标。在屏幕、打印机等设备上的坐标是二维坐标。值得一提的是，OpenGL可以只使用设备的一部分进行绘制，这个部分称为视区或视口(viewport)。投影得到的是视区内的坐标(投影坐标)，从投影坐标到设备坐标的计算过程就是设备变换了。

我们在OpenGL ES中常用到的几种坐标系：世界坐标系、物体坐标系、设备坐标系、眼坐标系当然还有假想的纹理坐标系

几何数据——顶点位置，和标准向量(normal vectors),在OpenGL 管道raterization 处理过程之前可通过顶点操作(Vertex Operation)和基本组合操作改变这些数据。

1 .物体或模型坐标系Object Coordinates or model Coordinates对应的ModelMatrix
对象的本地坐标系——任何变换之前的最初位置.为了变换(transformation)这些对象，可以调用glRotate(),glTranslatef(),glScalef()这些方法。
从object coordainates到world coordinates再到camera coordinate的变换，在OpenGL中统一称为model-view转换，初始化的时候，object coordinates和world coordinates还有camera coordinates坐标重合在原点，变换矩阵都为Identity,所以在OpenGL中用glLoadIdentity()初始化变换矩阵栈。model-view matix转换points,vectorsd到camera坐标系。

2. 世界坐标系（World coordinates）对应的是WorldMatrix的Matrix
在OpenGL中，世界坐标系是以屏幕中心为原点(0, 0, 0)，且是始终不变的。你面对屏幕，你的右边是x正轴，上面是y正轴，屏幕指向你的为z正轴。长度单位这样来定：窗口范围按此单位恰好是(-1,-1)到(1,1)，即屏幕左下角坐标为（-1，-1），右上角坐标为（1,1）。这是采用了归一化的结果
使用GL_MODELVIEW矩阵和Object 坐标相乘所得。在OpenGL中用GL_MODELVIEW将对象对象空间(Object Space)变换到视觉空间(eye space)。GL_MODELVIEW

矩阵是模型矩阵（Model Matrix）和视觉矩阵（View Matrix）的组合 (Mview * Mmodel)。其中，Model 变换指的是将Object Space转换到World Space

（译注：World Space值得是OpenGL中的三维空间），而View 变换是将World space变换到eye space。

3. 眼坐标或相机坐标（Eye (or Camera) coordinates) 对应的是ViewMatrix
以视点为原点，以视线的方向为Z+轴正方向的坐标系中的方向。OpenGL管道会将世界坐标先变换到眼坐标，然后进行裁剪，只有在视线范围(视见体)之内的场景才会进入下一阶段的计算。

4.剪切面坐标系（Clip Coordinates）对应的ProjectionMatrix
由眼坐标可知，OpenGL管道首先会将目标从世界坐标变换到眼坐标，然后对视线范围外的部分进行裁剪。
裁剪过程中用到投影变换矩阵栈(ProjectionMatrix)，栈顶矩阵就是当前投影变换矩阵，负责将场景各坐标变换到眼坐标，由所得到的结果是裁剪后的场景部分，称为裁剪坐标

我们上面说到了ModelViewMatrix 与ProjectionMatrix两个矩阵栈，那矩阵栈是怎么切换的呢？
用函数：glMatrixMode(GL_MODELVIEWING或GL_PROJECTION);本命令执行后参数所指矩阵栈就成为当前矩阵栈，以后的矩阵栈操纵命令将作用于它。
紧接着glMatrixMode()就是初始化矩阵，我们在上面也讲到，所有矩阵都为Identity,所以用方法glLoadIdentity()初始化矩阵。

5.标准设备坐标系（Normalized device coordinates）（NDC）
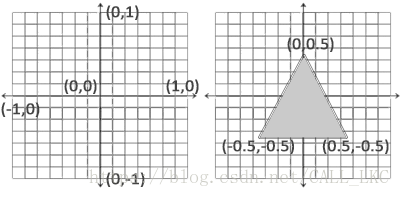
一旦你的顶点坐标已经在顶点着色器中处理过，它们就应该是标准化设备坐标了，标准化设备坐标是一个x、y和z值在-1.0到1.0的一小段空间。任何落在范围外的坐标都会被丢弃/裁剪，不会显示在你的屏幕上。下面你会看到我们定义的在标准化设备坐标中的三角形(忽略z轴)：

6. 屏幕坐标系（Window (or screen) coordinates）
屏幕坐标系，主要有两种，

第一种：以左上角为原点。代表的操作系统有Windows，Android，Symbian，iOS 的Core Graphics如图1左侧。

第二种：以左下角为原点。比如iOS的CGContextDrawImage，如图2右侧。

7. 视口坐标系（ViewPort coordinates）
视口坐标系是与屏幕坐标系息息相关的，它是将 Game视图的屏幕坐标系单位化，即左下角为(0, 0)，右上角为(1, 1)，z轴坐标是相机的世界坐标中z轴坐标的负值

假如说屏幕坐标系左下角是（0,0）， 右上角是 （800,600）。 现在在一个点在屏幕坐标系上的坐标为 （200,450）。 现在我们把该点的坐标单位化为： x = =( 200/800 = 0.25), y == ( 450 / 600 = 0.75 ), 最终该点单位化的结果坐标为 （0.25,0.75，0）

.8. 纹理坐标系(Texture coordinates)
它的坐标系以纹理左下角为坐标原点，向右为x正轴方向，向上为y轴正轴方向。他的总长度是1。即纹理图片的四个角的坐标分别是：(0,0)、(1,0)、(0,1)、(1,1)，分别对应左下、右下、左上、右上四个顶点。

9 . 齐次坐标（Homogeneous Coordinates）
其次坐标这个概念在第一次看real-time rendering 这本书的时候就有提起到，但当时看的一头雾水，只知道其次坐标在某些计算中比较方便，而事实上齐次坐标有着非常重要的意义和作用，主要是在处理三维透视方面，常用的几个地方，比如texture mapping 透视矫正，Projection Matrix的计算等等。

在笛卡尔坐标系中，两条平行线是永不相交的，而在现实中，两条平行线是可能相交于一点的，比如说下面的铁轨。

在这种透视空间中，笛卡尔坐标就无法描述了。

解决方案就是齐次坐标，一句话解释，就是用N+1个数来表示N维空间中的点。

比如一个二维坐标(X,Y),它的齐次坐标就是(x, y, w), 关系如下

X = x/w
Y = y/w
所以在知道齐次坐标的情况下，可以很方便地得到其笛卡尔坐标。之所以称之为其次坐标，是因为奇次坐标具有缩放不变性，比如(1,2,3),(2,4,6), (1a,2a,3a) 所表达的笛卡尔坐标是一样的！

有了其次坐标我们就可以证明两条平行线相交了。

有两条直线

Ax + By + C = 0

Ax + By + D = 0

很明显他们在平面内是平行线，永不相交（如果C==D的话，两条直线就重合了）

化为其次坐标，

A(x/w) + B(y/w) + C = 0;

A(x/w) + B(y/w) + D = 0;

同乘w，得到

Ax + By + Cw = 0

Ax + By + Dw = 0

则有解 (x,y,0)，所以两条平行线相交在（x,y,0），也就是相交在无穷远的点。

一. ModelMatrix
在openGL中，每一个GameObject上面都会有一个Transform，用来记录这个Object的position，rotation和scale. 这里借用Unity3D工具

这三项都可以用矩阵来表示，位移矩阵是

旋转矩阵由Quatenion转过来

R = (
1.0f - 2.0fyy - 2.0fzz, 2.0fxy - 2.0fzw, 2.0fxz + 2.0fyw, 0.0f,
2.0fxy + 2.0fzw, 1.0f - 2.0fxx - 2.0fzz, 2.0fyz - 2.0fxw, 0.0f,
2.0fxz - 2.0fyw, 2.0fyz + 2.0fxw, 1.0f - 2.0fxx - 2.0fyy, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
)

缩放矩阵

具体的矩阵推导可以参考拳四郎之前写的Real-Time Rendering (2) - 变换和矩阵（Transforms and Matrics）。Real-Time Rendering (2) - 变换和矩阵（Transforms and Matrics）

所谓的ModelMatrix，就是将模型坐标变换到WorldMatrix的Matrix，

WorldMatrix = Mt * Mr * Ms

Vw = WorldMatrix * Vm

注意这里的Matrix都是列主序， Vm是Model坐标系下的坐标，Vw是世界坐标系下的坐标，矩阵是右乘Vm， Vm用的齐次坐标，w = 1.

顺序一定是TRS。

二 . ViewMatrix
ViewMatrix用于直接将World坐标系下的坐标转换到Camera坐标系下。已知相机的坐标系，还有相机在世界空间下的坐标.就可以求出ViewMatrix，下面进行具体推导。

令UVN为相机坐标系下的三个基，，对于一个相机来说，它在开始的时候和世界坐标系是重合的，用户控制相机在世界空间中移动之后，相机的状态可以用两个属性来描述——朝向和位置。也就是说，有了这两个属性，一个相机模型在世界中的状态就确定了。而这两个属性，我们用变换的理论来描述，就是旋转和平移。可以想象，对于世界中的任何一个相机状态，我们都可以把它看成是：相机先围绕自身基原点旋转一定的角度，然后平移到世界空间的某个地方。下图展示了这个过程

图中，红色是相机的基，而黑色是世界的基，也就是参考系。小人是世界中的一个物体。相机在移动之前，两个基是重合的。当相机在屏幕中定位时，它首先会进行朝向的确定——旋转，然后进行位置的确定——平移。图中的Rotation和Translation两步就是相机定位时所发生的变换。可以看到相机相对于小人的运动。而当进行相机变换的时候，小人应该从世界基变换到相机的基里面。这样，他应该进行一个相机定位的逆定位，先逆平移小人和相机，然后再逆旋转小人和相机，最后相机归位，小人随相机变到了相机空间。这是由Inverse Translation和Inverse Rotation两个步骤完成的，这两个步骤就是相机变换。现在我们推导这个变换。我们把关系写出来，相机本身的变换C包括两个元素

C = TR

其中T是平移变换，R是旋转变换。而相机变换是相机本身变换的逆变换

这个C^{-1就是我们要求出的相机变换。其中T}-1很容易求出，即

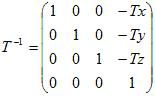
R^(-1)比较难求出，这里用到了正交基一些知识，可以参考下碰撞检测之Ray-Cylinder检测前面关于正交基的部分。Ray-Cylinder

当相机变换进行完Inverse Translation这一步之后，相机的原点和世界原点就重合了，也就是处理完了关于平移的变换。接下来我们要做的是逆旋转，而其实逆旋转的目的，就是要得到目前世界坐标中经过逆平移的小人在相机坐标系中的坐标。

由坐标转换公式

对于世界坐标中的已经经过逆平移的坐标v’，它在相机坐标系R中的坐标是v’’，而相机坐标系就是

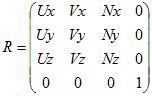
则相机变换的完整公式就是

其中v是小人在世界空间中的坐标，v’’是小人在相机空间中的坐标。则相机变换矩阵就是

常见的求ViewMatrix的情况有三种，一种是用LookAt函数，第二种是类似FPS游戏中通过pitch和yaw来算，还有一种是类似轨迹球的算法。
最后的方法都是转化为求出相机的坐标系的基。

三. ModelViewMatrix
模型视图矩阵是视图变换矩阵与模型变换矩阵相乘的结果。每个视图或模型变换都创建了一个新的矩阵，并与当前的模型视图矩阵相乘，其结果成为新的当前矩阵，表示组合后的变换。模型视图矩阵堆栈至少可以包含32个4×4的矩阵。模型视图矩阵一开始的顶部矩阵是单位矩阵。有些OpenGL实现支持在矩阵堆栈上保存超过32个的矩阵。为了确定矩阵堆栈的最大允许矩阵数，可以使用查询函数glGetIntegerv(GL_MAX_MODELVIEW_STACK_DEPTH, GLint *params)。

四. ProjectionMatrix
投影矩阵将视图坐标系中的顶点转化到平面上。
实际上，投影矩阵先把顶点坐标转化到规范立方体坐标系(Xc-Yc-Zc)中，也就是将四棱锥台体空间映射到规范立方体中。规范立方体是x，y，z都处在区间[-1,1]之间的边长为2的立方体，如下所示。顶点在其中的坐标，其x值和y值直接就是顶点在屏幕上的坐标，而z坐标值可以用来表示顶点深度，如果两个不同顶点投影到平面上时重合了，深度可以来确定那个点在前面。
根据投影矩阵×视图矩阵×模型矩阵求出模型视图投影矩阵，顶点坐标乘以该矩阵就直接获得其在规范立方体中的坐标了。这个矩阵通常作为一个整体出现在着色器中。

五. NormalMatrix
与自己的共轭转置矩阵满足交换律的复系数方块矩阵：
如果A为实系数矩阵，则只需满足条件
矩阵的正规性是检验矩阵是否可对角化的一个简便方法：任意正规矩阵都可在经过一个酉变换后变为对角矩阵，反过来所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵。
在复系数矩阵中，所有的酉矩阵、埃尔米特矩阵和斜埃尔米特矩阵都是正规的。同理，在实系数矩阵中，所有的正交矩阵、对称矩阵和斜对称矩阵都是正规的。
正规矩阵还包括除上述特例外的其它矩阵。

参考：
1.化作春泥_
2. 安静的Sunny
3. 拳四郎
4. http://blog.sina.com.cn/s/blog_43699c540101o1wu.html
5. [拳四郎](https://blog.csdn.net/silangquan/article/details/9970673)