深度学习(1)---卷积神经网络
文章目录
- 一、发展历史
-
- 1.1 CNN简要说明
- 1.2 猫的视觉实验
- 1.3 新认知机
- 1.4 LeNet-5
- 1.5 AlexNet
- 二、卷积层
-
- 2.1 图像识别特点
- 2.2 卷积运算
- 2.3 卷积核
- 2.4 填充和步长
- 2.5 卷积计算公式
- 2.6 多通道卷积
- 三、池化层
一、发展历史
1.1 CNN简要说明
1. 卷积神经网络(Convolutional Neural Networks,CNN)是一种专门针对图像领域任务提出的神经网络,它通过多个卷积层和池化层来对输入图像进行特征提取和分类。自2012年以来,卷积神经网络在大部分图像任务中表现出了卓越的性能,例如图像分类、图像分割、目标检测、图像检索等。
2. 卷积神经网络的基本结构包括输入层、卷积层、池化层和全连接层。其中,卷积层负责在输入图像上进行卷积运算,提取局部特征;池化层则用于减小特征图的尺寸,从而减少计算量和避免过拟合;全连接层则用于将前面各层的特征进行组合,产生具有更高级别的特征表示。
3. 卷积神经网络的优点在于:它可以自动提取图像中的特征,不需要手工设计特征;它可以处理高维度的图像输入,具有很强的通用性;同时,卷积神经网络具有较强的鲁棒性和容错性,能够有效地处理噪声和干扰。
1.2 猫的视觉实验
1. 卷积神经网络的发展,最早可以追溯到 1962 年,Hubel 和 Wiesel 对 猫大脑中的视觉系统的研究 。他们首次发现猫的视觉系统中存在层级结构,并且发现了两种重要的细胞simple cells和complex cells,不同类型的细胞承担不同抽象层次的视觉感知功能。
Simple cells和complex cells是视觉皮层中的两种不同类型的细胞。
Simple cells(简单细胞)是视皮层中一种具有简单功能、对视觉刺激产生简单反应的神经元。它们主要接收来自视网膜的信号,对视野中的某种特定特征,如方向、颜色或形状等,产生反应。
与simple cells相比,complex cells(复杂细胞)具有更复杂的功能,能够对更复杂的视觉刺激产生反应。它们不仅能对特定的方向、颜色或形状产生反应,还能对更复杂的视觉信息如运动、纹理等产生反应。
总的来说,视觉皮层中的simple cells和complex cells是两种不同类型的神经元,它们各自具有其特殊的视觉功能和反应机制。
2. 实验过程:(1)在猫脑上打开3mm,插入电极。(2)让猫看各种形状、位置、亮度和运动的光条。(3)观察大脑视觉神经元激活情况。

3. 通过实验得到的一些结论:(1)神经元细胞存在局部感受区域(receptive field),也称为感受野,是神经元对特定刺激产生反应的感受区域。(2)细胞对角度有选择性。(3)细胞对运动方向有选择性。
4. 对CNN的启发:(1)视觉系统是一个分层次和分阶段进行处理的过程,从低级到高级的抽象过程→堆叠使用卷积和池化。(2)神经元细胞实际上是存在局部感受区域的,具体来说它们是局部敏感→神经元局部连接。
1.3 新认知机
1. 在上述实验的启发下,日本科学家福岛邦彦提出了神经认知模型。福岛邦彦说:人类的视觉神经是分层的。首先,物体发出或者反射的光进入眼睛,通过瞳孔晶状体等照射到视网膜上成像,然后视网膜上的感光细胞会将图像转化为神经冲动传递到大脑。
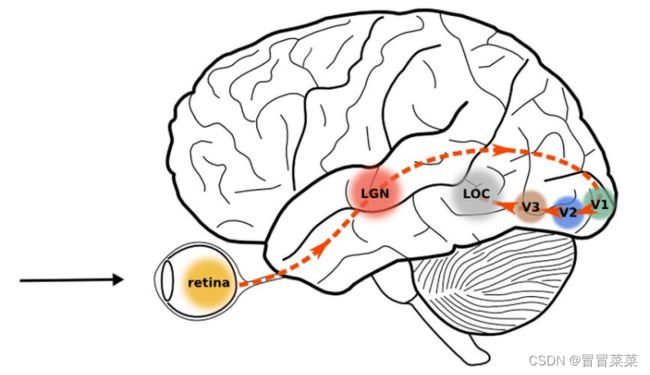
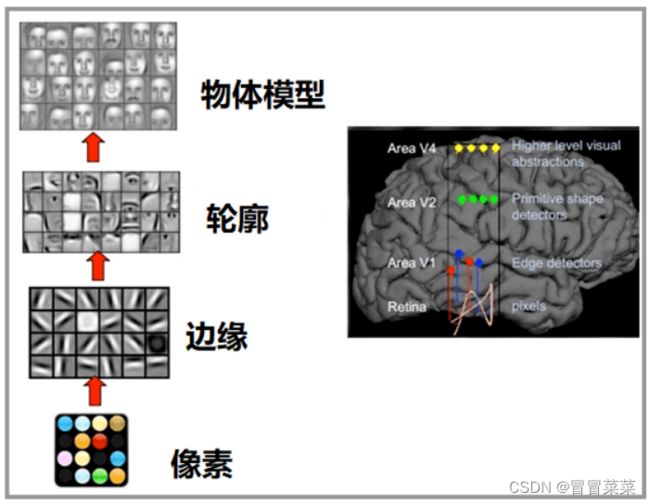
2. 大脑最初接受视觉信号的神经皮层叫做初级皮层V1,它所获得的是一大堆像素点;随后,V1皮层会把处理过的信号传递到V2皮层,V2皮层会得到图像的边缘、方向等信息;V2皮层再次对信号进行处理,进入V3皮层,在这里神经元会获得物体的轮廓、细节等信息…信号经过多个皮层的传递,最终抽象出物体的大量特征,从而做出判断。
3. 日本科学家福岛邦彦于1988年提出的一个卷积神经网络的雏形----新认知机(Neocognitron)该模型采用了基于局部感受野的卷积操作,通过无监督学习进行特征的层次聚类,从而实现了对于输入图像的识别和分类。新认知机是一种八层前馈网络,包括输入层、两个卷积层、两个池化层(下采样层)、两个全连接层和一个输出层。新认知机是卷积神经网络的一个重要基础,后来的卷积神经网络模型,例如LeNet-5和AlexNet等,都采用了类似的结构和设计思路。
1.4 LeNet-5
1. LeNet-5是由Yann LeCun等人于1998年提出的一种卷积神经网络,它是第一个大规模商用的卷积神经网络。LeNet-5在手写邮政编码识别方面取得了显著的成功,并被广泛应用于美国邮政系统。
2. 下图是LeCun在原始论文中的一张结构图。如果不计输入层,该模型共7层,包括2个卷积层,2个池化层,3个全连接层。
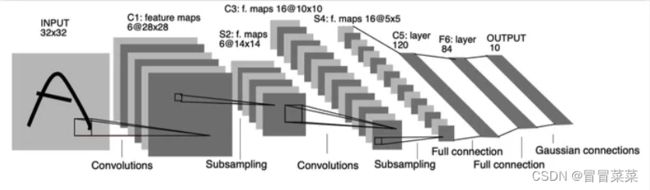
3. LeNet5这个网络虽然很小,但是它包含了深度学习的基本模块:卷积层,池化层,全连接层,是其它深度学习模型的基础。
1.5 AlexNet
1. AlexNet是第一个震惊整个计算机视觉领域的卷积神经网络。由亚历克斯·克罗素(Alex Krizhevsky)和团队在2012年提出,并在当年的ImageNet图像分类挑战赛中取得了突破性的成绩,使得卷积神经网络成为计算机视觉领域的热门研究课题。

2. 上图为AlexNet原始的网络结构图,可以发现看起来并不是那么的直观明了。同时,受限于当时GPU缓存的大小,所以当时在训练这一网络时,将其分成了上下两个部分分别在不同的GPU上运算。但是,我们现在就大可不必这样做,直接合并在一起即可。因此,我们可以重新将其画成如下形式:
二、卷积层
2.1 图像识别特点
1. 特征具有局部性。比如老虎头部的 “王字” 只出现在老虎的头部区域。

2. 特征可能出现在图像的任意位置。比如下面这张老虎的图片和上面的图片的特征位置不一样。

3. 下采样图像,不会改变图像的类别和目标。如下面的图片虽然尺寸变了,但是类型和特征不变。
2.2 卷积运算
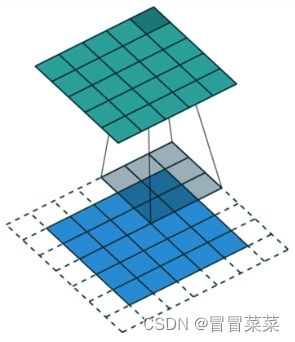
卷积运算是指从图像的左上角开始,开一个与卷积核同样大小的活动窗口,窗口图像与卷积核像元对应起来相乘再相加,并用计算结果代替窗口中心的像元亮度值。然后,活动窗口向右移动一列,并作同样的运算。以此类推,从左到右、从上到下,即可得到一幅新图像。
![]()
2.3 卷积核
1. 卷积核是图像处理时给定输入图像,输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素,其中权值由一个函数定义,这个函数称为卷积核。卷积核是一个权矩阵,与使用的图像区域大小相同。
2. 卷积核对图像进行处理之后。相当于对图像进行了特征提取,输出通常成为特征图。
3. 如下面图片中:
- 第一个卷积核是边缘识别类卷积核。这类卷积核的共同特征是:卷积核内所有的值求和为0,这是因为边缘的区域,图像的像素值会发生突变,与这样的卷积核做卷积会得到一个不为0的值。而非边缘的区域,像素值很接近,与这样的卷积核做卷积会得到一个约等于0的值。
- 第二个卷积核是锐利化卷积核。这类卷积核的作用是凸显像素值有变化的区域,使得本来像素值梯度就比较大的区域(边缘区域)变得像素值梯度更大。在边缘检测中,卷积核的设计要求卷积核内的所有值求和为0,这里的要求刚好相反,要求卷积核内的所有值应该不为0,凸显出像素值梯度较大的区域。
- 第三个卷积核是模糊化卷积核。这类卷积核的作用原理是对一片区域内的像素值求平均值,使得像素变化更加平缓,达到模糊化的目的。
import torch
from PIL import Image
import torchvision
image = Image.open('girl.png').convert('RGB') #导入图片
image_to_tensor = torchvision.transforms.ToTensor() #实例化ToTensor
original_image_tensor = image_to_tensor(image).unsqueeze(0) #把图片转换成tensor
#卷积核:prewitt横向
conv_prewitt_h = torch.nn.Conv2d(in_channels=3,out_channels=1,kernel_size=3,padding=0,bias=False) #bias要设定成False,要不然会随机生成bias,每次结果都不一样
conv_prewitt_h.weight.data = torch.tensor([[[[-1,-1,-1],[0,0,0],[1,1,1]],
[[-1,-1,-1],[0,0,0],[1,1,1]],
[[-1,-1,-1],[0,0,0],[1,1,1]]]], dtype=torch.float32)
#卷积核:模糊化
conv_blur = torch.nn.Conv2d(in_channels=3,out_channels=1,kernel_size=5,padding=0,bias=False)
conv_blur.weight.data = torch.full((1,3,5,5),0.04)
#卷积核:锐利化
conv_sharp = torch.nn.Conv2d(in_channels=3,out_channels=1,kernel_size=3,padding=0,bias=False)
conv_sharp.weight.data = torch.tensor([[[[-1,-1,1],[-1,-1,-1],[-1,-1,-1]],
[[-1,-1,1],[-1,22,-1],[-1,-1,-1]],
[[-1,-1,1],[-1,-1,-1],[-1,-1,-1]]]], dtype=torch.float32)
#生成并保存图片
tensor_prewitt_h = conv_prewitt_h(original_image_tensor)
torchvision.utils.save_image(tensor_prewitt_h, 'prewitt_h.png')
tensor_blur = conv_blur(original_image_tensor)
torchvision.utils.save_image(tensor_blur, 'blur.png')
tensor_sharp = conv_sharp(original_image_tensor)
torchvision.utils.save_image(tensor_sharp, 'sharp.png')
(1)原图:
2.4 填充和步长
1. 填充(Padding):输入图像与卷积核进行卷积后的结果中会损失部分值,输入图像的边缘被“修剪”掉了(边缘处只检测了部分像素点,丢失了图片边界处的众多信息)。这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(Padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用“0”来进行填充的。
2. 填充的作用:(1)使卷积后图像分辨率保持不变,方便计算特征图尺寸的变化。(2)弥补边界信息的 “丢失” 问题。
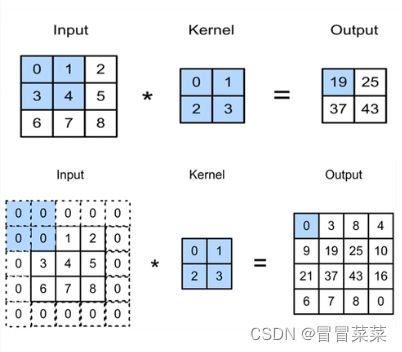
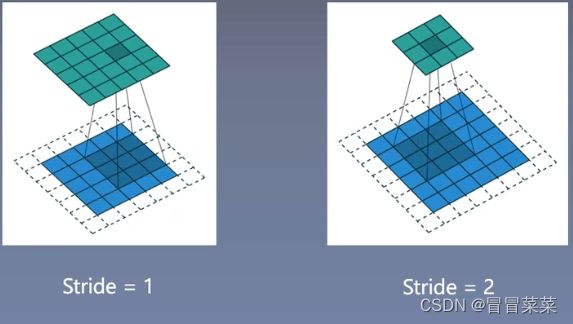
3. 步长(Stride):滑动卷积核时,我们会先从输入的左上角开始,每次往左滑动一列或者往下滑动一行逐一计算输出,我们将每次滑动的行数和列数称为Stride。在之前的图片中,Stride=1;在下图中,Stride=2。

4. Stride的作用是:成倍缩小尺寸,而这个参数的值就是缩小的具体倍数。比如步幅为2,输出就是输入的1/2;步幅为3,输出就是输入的1/3;以此类推。
2.5 卷积计算公式
1. 计算公式:
输入图片的尺寸:一般用n*n表示输入的image大小。
卷积核的大小:一般用 f*f表示卷积核的大小。
填充(Padding):一般用 p来表示填充大小。
步长(Stride):一般用 s来表示步长大小。
输出图片的尺寸:一般用 o来表示。
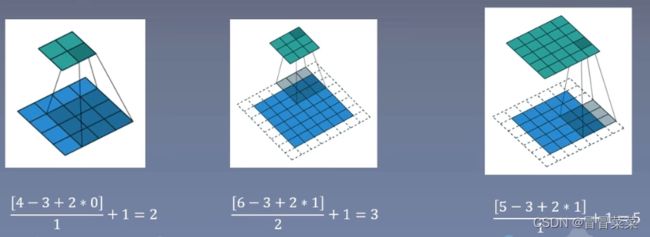
如果这些都已知,可以求得计算公式如下,其中的符号是向下取整符号,用于结果不是整数时进行向下取整。
2.6 多通道卷积
1. 上述例子都只包含一个输入通道,而实际上大多数输入图像都有 RGB 3个通道。
RGB是一种颜色模型,它代表了红色(R)、绿色(G)和蓝色(B)三种基本颜色的组合。通过调整这三种颜色的强度和亮度,可以创建出各种不同的颜色。在计算机图形学和数字图像处理中,RGB是最常用的颜色表示方法之一。每个颜色通道的取值范围为0-255,表示颜色的强度,通过不同通道的组合可以得到大约1600万种不同的颜色。
通过调整RGB中每个通道的值,可以混合和匹配不同的颜色,从而对图像进行卷积操作。举个例子,假设有一张彩色图片,我们可以使用RGB模式来获取每个像素点的颜色信息,然后通过卷积算法对图像进行处理。
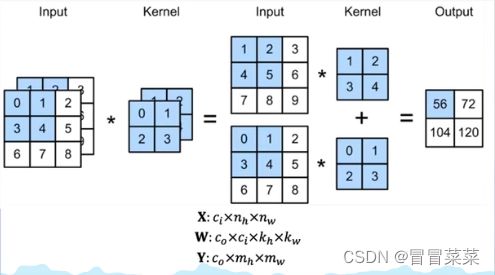
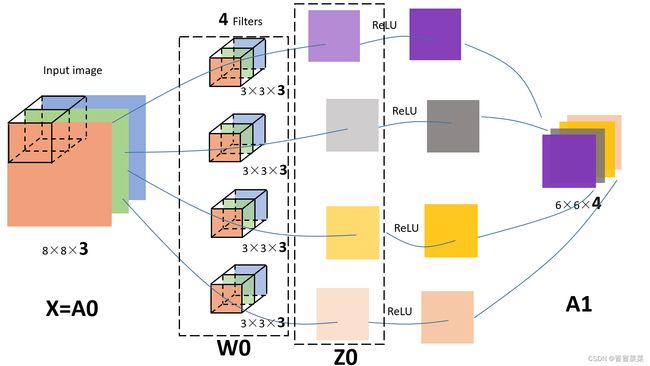
2. 多通道卷积的计算过程如下:
- (1)将卷积核与输入数据的每个通道对应进行点积运算。这涉及到将卷积核的每个元素与输入数据的相应元素相乘,然后将所有乘积相加。
- (2)将步骤(1)中的结果相加,得到卷积的结果。
- (3)将步骤(2)中的结果存储在输出特征图的相应位置。
- (4)通过滑动卷积核并重复步骤(1)到(3),直到遍历输入数据的所有位置,从而计算输出特征图的所有值。
3. 下面这些图片可以帮助理解上面的过程:
三、池化层
1. 池化:一个像素表示一块区域的像素值,降低图像的分辨率。
2. 池化层:池化层是深度学习中常用的一种层级结构,它可以对输入数据进行降采样,减少数据量,同时保留重要的特征信息。池化层通常紧跟在卷积层之后,可以有效地减少数据量和计算复杂度,提高模型的训练速度和泛化能力。
3. 池化层的结构与卷积层类似,它也由多个滤波器组成,每个滤波器对输入数据进行卷积操作,得到一个输出特征图。不同的是,池化层的卷积操作通常不使用权重参数,而是使用一种固定的池化函数,例如最大池化、平均池化等。
4. 池化层的作用:(1)缓解卷积层对位置的过度敏感。(2)减少冗余,降低图像的分辨率,从而减少参数量。

5. 池化层的分类:最大池化(max pooling)、平均池化(average pooling)、重叠池化(OverlappingPooling)、空金字塔池化(Spatial Pyramid Pooling)。
- 最大池化(max pooling):选图像区域的最大值作为该区域池化后的值。
- 平均池化(average pooling):计算图像区域的平均值作为该区域池化后的值。
- 重叠池化(OverlappingPooling):相邻池化窗口之间有重叠区域,此时一般sizeX > stride。
- 空金字塔池化(Spatial Pyramid Pooling):将一个pooling变成了多个scale的pooling,用不同大小池化窗口作用于上层的卷积特征。
6. 如下图是一个最大池化和平均池化: