JavaSE-自定义队列+两栈实现队列+两队列实现栈

1.顺序队列实现

与栈一样，队列也是一种操作受限制的线性表，但与栈不同的是，栈是后进先出，队列的特点是先进先出。

实现与栈类似，队列有一个队头指针和一个队尾指针，入队的时候利用队尾指针进行尾插，出队的时候利用队头指针，把队头指针对应数组中的元素赋值为null，防止内存溢出。

class OrderQueue{
    private int header; //队头位置
    private int tail; //队尾位置
    private int size; //有效元素
    private T[] queueArrays;
    private static final int defaultcapacity = 5;

    public OrderQueue(){
        this(defaultcapacity);
    }

    public OrderQueue(int capacity){
        this.queueArrays = (T[])new Object[capacity];
    }

    //入队
    public boolean enqueue(T value){
        //判满
        if(isFull()){
            //扩容
            if(size == queueArrays.length){
                queueArrays = Arrays.copyOf(queueArrays, queueArrays.length*2);
            }else{
                System.arraycopy(queueArrays, header, queueArrays, 0, size);
            }
        }
        queueArrays[tail++] = value;
        size++;
        return true;
    }

    public boolean isFull(){
        return tail == queueArrays.length;
    }

    //出队
    public T dequeue(){
        if(isEmpty()){
            throw new UnsupportedOperationException("the queue has been empty");
        }
        T result = queueArrays[header];
        queueArrays[header++] = null;
        size--;
        return result;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public void show(){
        for(int i=header; i

2. 循环队列实现

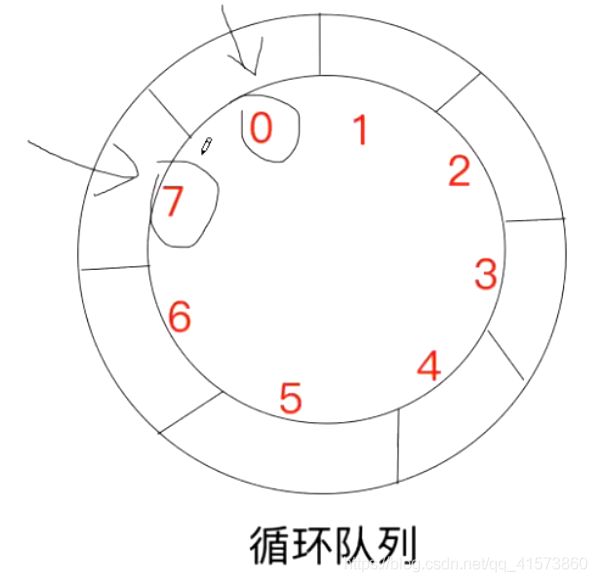
循环队列是把顺序队列首尾相连，把存储队列元素的表从逻辑上看成一个环，成为循环队列。图中有两个名义上的队头head队尾tail指向0和7。

对于循环队列存在一种特殊现象：假溢出。设队头指针为head，队尾指针是tail，约定head指向队头元素的前一位置，tail指向队尾元素。当head等于-1时队空，tail等于m-1时为队满。由于队列的性质（“删除”在队头而“插入”在队尾），所以当队尾指针tail等于m-1时，若head不等于-1，则队列中仍有空闲单元，所以队列并不是真满。这时若再有入队操作，会造成假“溢出”。

解决假溢出：

当添加一个元素时,(tail+1)%MAXSIZE;

当删除一个元素时，(head+1)%MAXSIZE;

当head=front的时候，队列可能是满，也可能是空。

　　因为存在满和空两种情况，需要分别判断：

　　满：当队列添加元素到tail的下一个元素是head的时候，也就是转圈子要碰头了，就认为队列满了。(Q.tail+1)%MAXSIZE=Q.head

　　空：当队列删除元素到head=rear的时候，认为队列空了。Q.tail==Q.head,不一定为0

实现过程：

class LoopQueue{
    private int header; //队头位置
    private int tail; //队尾位置
    private T[] queueArrays;
    private static final int defaultcapacity = 5;

    public LoopQueue(){
        this(defaultcapacity);
    }

    public LoopQueue(int capacity){
        this.queueArrays = (T[])new Object[capacity];
    }

    //入队
    public boolean enqueue(T value){
        //判满
        if(isFull()){
            //扩容
            queueArrays = Arrays.copyOf(queueArrays, queueArrays.length*2);
        }
        queueArrays[tail] = value;
        tail = (tail+1) % queueArrays.length;
        return true;
    }

    public boolean isFull(){
        return (tail+1)%queueArrays.length == header;
    }

    //出队
    public T dequeue(){
        if(isEmpty()){
            throw new UnsupportedOperationException("the queue has been empty");
        }
        T result = queueArrays[header];
        queueArrays[header] = null;
        header = (header+1) % queueArrays.length;
        return result;
    }

    public boolean isEmpty(){
        return header == tail;
    }

    public void show(){
        for(int i=header; i

3. 两个栈实现队列的入队出队

思路：首先定义两个栈，称为栈1和栈2，在进行入队操作的时候直接将元素入栈1，出栈的时候出栈2的栈顶，如果栈2为空的话就将栈1的元素入到栈2中，再进行出栈，两次入栈操作就能完成队列的先进先出操作，如果两个栈都为空的话就抛出异常。

    public static Stack stack1 = new Stack<>();
    public static Stack stack2 = new Stack<>();
    public static void pushQueue(int value){
        stack1.push(value);
    }

    public static int popQueue(){
        if(stack1.isEmpty() && stack2.isEmpty()){
            throw new UnsupportedOperationException("the stack has been empty");
        }
        if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }

4.两个队列实现栈的入栈出栈

思路：先定义两个队列，称为队1和队2，LinkedList类型是可以对两端进行操作的。入栈时，起初两个队列都为空，可以先将元素入队1，出队的时候将队1的元素用一个临时队列存储起来，将队中length-1个元素入到另一个临时队列，此时队列中还剩一个元素，对它进行出栈即可。

    public static Queue queue1 = new LinkedList<>();
    public static Queue queue2 = new LinkedList<>();
    public static void pushStack(int value){
        if(queue1.isEmpty() && queue2.isEmpty()){
            queue1.add(value);
        }else if(queue1.isEmpty()){
            queue2.add(value);
        }else{
            queue1.add(value);
        }
    }

    public static int popStack(){
        //popQueue是当前的数据队列
        Queue popQueue = queue1.isEmpty() ? queue2 : queue1;
        //pushQueue是当前的辅助队列
        Queue pushQueue = queue1.isEmpty() ? queue1 : queue2;

        while(popQueue.size() > 1){
            pushQueue.add(popQueue.remove());
        }
        return popQueue.remove();
    }