论文笔记 Inference in Deep Gaussian Processes using Stochastic Gradient Hamiltonia使用随机梯度哈密顿量蒙特卡罗推理深度高斯过程

使用随机梯度哈密顿量蒙特卡罗推理深度高斯过程

0.摘要

深度高斯过程 (DGP) 是高斯过程的层次概括，它将经过良好校准的不确定性估计与多层模型的高度灵活性相结合。 这些模型的最大挑战之一是精确推断是难以处理的。 当前最先进的推理方法变分推理 (VI) 对后验分布采用高斯近似。 这可能是一般多峰后验的潜在较差的单峰近似。 在这项工作中，我们为后验的非高斯性质提供了证据，并且我们应用随机梯度哈密顿蒙特卡罗方法来生成样本。 为了有效地优化超参数，我们引入了移动窗口 MCEM 算法。 与 VI 对应物相比，这会以更低的计算成本产生明显更好的预测。 因此，我们的方法为 DGP 中的推理建立了新的最新技术。

1.介绍

深度高斯过程 (DGP) [Damianou and Lawrence, 2013] 是高度灵活的多层预测模型，可以准确地模拟不确定性。 特别是，它们已被证明在从小型（500 个数据点）到大型数据集（500,000 个数据点）的众多监督回归任务中表现良好 [Salimbeni 和 Deisenroth，2017，Bui 等，2016，Cutajar 等 ., 2016]。 与神经网络相比，它们的主要优势在于它们能够捕捉预测中的不确定性。 这使它们成为预测不确定性起关键作用的任务的理想候选者，例如黑盒贝叶斯优化问题和各种安全关键应用，如自动驾驶汽车和医疗诊断。

深度高斯过程为高斯过程 (GP) [Williams and Rasmussen, 1996] 引入了多层层次结构。 GP 是一种非参数模型，它假设任何有限输入集的联合高斯分布。 任何一对输入的协方差由协方差函数确定。 由于非参数和可分析计算，GPs 可能是一个稳健的选择，但是，一个问题是选择协方差函数通常需要手动调整和数据集的专家知识，如果没有手头问题的先验知识，这是不可能的。 在多层层次结构中，隐藏层通过拉伸和扭曲输入空间来克服这一限制，从而产生贝叶斯“自调整”协方差函数，无需任何人工输入即可拟合数据 [Damianou, 2015]。

GP 的深度层次化泛化是以完全连接的前馈方式完成的。 前一层的输出用作下一层的输入。 然而，与神经网络的一个显着区别是层输出是概率而不是精确值，因此不确定性通过网络传播。 图 1 的左侧部分说明了具有单个隐藏层的概念。 隐藏层的输入是输入数据 x，隐藏层 f1 的输出作为输出层的输入数据，输出层本身是由 GPs 形成的。

图 1：（左）：深度高斯过程插图 1。 （中）：随机选择诱导输出的直方图。 最佳拟合高斯分布用虚线表示。 其中一些表现出明显的多模式行为。 （右）：每个数据集 100 个随机选择的诱导输出的 P 值。 零假设是它们的分布是高斯分布。

由于使用逆协方差矩阵的计算成本很高，因此在大型数据集的 GP 中进行精确推断是不可行的。 相反，使用一小组伪数据点 (100) 来近似后验，也称为诱导点 [Snelson and Ghahramani, 2006, Titsias, 2009, Quinonero-Candela and Rasmussen, 2005]。 我们在整篇论文中都假设这个诱导点框架。 使用诱导点进行预测以避免计算整个数据集的协方差矩阵。 在 GP 和 DGP 中，诱导输出都被视为需要边缘化的潜在变量。

DGP 中当前最先进的推理方法是双重随机变化推理 (DSVI) [Salimbeni 和 Deisenroth，2017]，它已被证明优于期望传播 [Minka，2001，Bui 等人，2016]，并且它 也比采用概率反向传播的贝叶斯神经网络 [Hern´andez-Lobato 和 Adams, 2015] 和采用早期推理方法的贝叶斯神经网络（如变异推理 [Graves, 2011]、随机梯度朗之万动力学 [Welling and Teh, 2011）和混合蒙特卡洛 [Neal, 1993]具有更好的性能。 然而，DSVI 的一个缺点是它用高斯近似后验分布。 我们非常自信地表明，对于我们在这项工作中检查的每个数据集，后验分布都是非高斯分布的。 这一发现促使使用具有更灵活后验近似的推理方法

在这项工作中，我们应用了一种新的 DGP 推理方法，即随机梯度哈密顿蒙特卡罗 (SGHMC)，这是一种准确有效地捕获后验分布的采样方法。 为了将基于采样的推理方法应用于 DGP，我们必须解决优化大量超参数的问题。 为了解决这个问题，我们提出了移动窗口蒙特卡罗期望最大化，这是一种获得超参数的最大似然 (ML) 估计的新方法。 该方法快速、高效且普遍适用于任何概率模型和 MCMC 采样器。

人们可能期望像 SGHMC 这样的采样方法比 DSVI 这样的变分方法在计算上更加密集。 然而，在 DGP 中，从后验采样成本很低，因为它不需要重新计算逆协方差矩阵，这仅取决于超参数。 此外，计算分层方差在 VI 设置中的成本更高。

最后，我们对各种监督回归和分类任务进行了实验。 我们凭经验表明，我们的工作以较低的计算成本显着改善了对中大型数据集的预测。

我们的贡献可以概括为三点。

1. 证明后验的非高斯性。 我们提供的证据表明，我们在这项工作中检查的每个回归数据集都有一个非高斯后验。
2. 我们使用 SGHMC 直接从 DGP 的后验分布中采样。 实验表明，这种新的推理方法优于以前的工作。
3. 我们介绍了移动窗口 MCEM，这是一种在使用 MCMC 采样器进行推理时有效优化超参数的新算法。

2.背景及相关工作

本节提供回归的高斯过程和深度高斯过程的背景，并建立本文中使用的符号。

2.1 单层GP

高斯过程由后验分布$f:R^D\to R$定义
输入$x=\{x_1,...,x_N\}$
输出$y=\{y_1,...,y_N\}$
在高斯过程模型下，假定$f=f(x)$是联合高斯且协方差函数为$k:R^D\times R^D\to R$，其中,$f(x)=\{f(x_1),...,f(x_N)\}$。
$y$条件分布由似然函数$p(y|f)$求得，常用：$p(y|f)=N(y|f,I{\sigma }^2)$

精确推理的计算成本是 $O(N^3)$，这使得它对于大型数据集在计算上是不可行的。 一种常见的方法是使用一组伪数据点 $Z=\{z_1,...,z_M\},u=f(Z)$[Snelson and Ghahramani, 2006, Titsias, 2009] 并将联合概率密度函数写为
$$p(y,f,u)=p(y|f)p(f|u)p(u)$$

给定诱导输出 $u$ 的 $f$ 的分布可以表示为 $p(f|u)=N(\mu ;\Sigma )$，其中
$$\mu =K_{xZ}{K}_{ZZ}^{-1}u$$
$$\Sigma =K_{xx}+K_{xZ}{K}_{ZZ}^{-1}{K}_{xZ}^T$$
为了获得 $f$ 的后验，$u$ 必须被边缘化，产生方程
$$p(f|y)=\int p(f|u)p(u|y)du$$
请注意，在给定 $u$ 的情况下，$f$ 有条件地独立于 $y$。

对于单层GPs,VI能够用于边际，VI使用变分后验$q(f,u)=p(f|u)q(u)$去近似联合后验分布$p(f,u|y)$，其中$q(u)=N(u|m,S)$。

$q(u)$ 的这种选择允许精确推断边际$q(f|m,S)=\int p(f|u)q(u)du=N(f|\hat{\mu },\hat{\Sigma })$

其中：
$$\hat{\mu }=K_{xZ}{K}_{ZZ}^{-1}m\text{\hspace{1em}(1)}$$
$$\hat{\Sigma }=K_{xx}+K_{xZ}{K}_{ZZ}^{-1}(K_{ZZ-S})K_{ZZ}^{-1}{K}_{xZ}^T\text{\hspace{1em}(1)}$$

需要优化变分参数和 S。 这是通过最小化真实后验和近似后验的 Kullback-Leibler 散度来完成的，这相当于最大化边缘似然的下界（证据下界或 ELBO）

$$\log p(y)\ge E_{q(f,u)}[\log p(y,f,u)-\log q(f,u)]=E_{q(f|m,S)}[\log p(y|f)]-KL[q(u)||p(u)]$$

2.2 深层GP

在深度为 $L$ 的 $DGP$ 中，每一层都是一个 $GP$，它对函数 $f_l$ 建模，其中输入 $f_{l-1}$ 和输出 $f_l$ 对于 $l=1,...,L(f_0=x)$如图 1 左侧所示。层的感应输入由 $Z_1,....,Z_L$ 表示，与之相关的感应输出 $u_1=f_1(Z_1),...,u_L=f_L(Z_L)$。

联合概率密度函数可以写成类似于 GP 模型的情况：
$$p(y,\{f_l{\}}_{l=1}^L,\{u_l{\}}_{l=1}^L)=p(y|f_L)\prod _{l=1}^{L}p(f_l|u_l)\text{\hspace{1em}(2)}$$

2.3 推理（暂略）

推理的目标是边缘化诱导输出$\{u_l{\}}_{l=1}^L$ 和层输出 $\{f_l{\}}_{l=1}^L$并逼近边际似然 $p(y)$。 本节讨论有关推理的先前工作。

双随机变分推理
DSVI 是对 DGP 的变分推理的扩展 [Salimbeni 和 Deisenroth，2017]，它用独立的多元高斯 $q(u_l)=N(u_l|m_l,S_l)$ 逼近诱导输出 $u_l$ 的后验。层输出自然遵循方程式1中的单层模型。
$$q(f_l|f_{l-1})=N(f_l|{\hat{\mu }}_l,{\hat{\Sigma }}_l)$$
$$q(f_L)=\int \prod _{l=1}^{L}q(f_l|f_{l-1})d{f}_{l}d{f}_{L-1}$$

然后通过小批量对层输出进行采样来估计生成的 ELBO 中的第一项，以允许扩展到大型数据集。$Likehood=E_{q(f_L)}[logp(y|f_L)]-{\prod }_{l=1}^{L}KL[q(u_l)||p(u_l)]$

高斯过程的基于采样的推理
在相关工作中，Hensman 等人。 [2015] 在单层 GP 中使用混合 MC 采样。 他们考虑了 GP 超参数和诱导输出的联合采样。 由于对 GP 超参数进行采样的成本很高，因此这项工作不能直接扩展到 DGP。 此外，它使用昂贵的方法贝叶斯优化来调整采样器的参数，这进一步限制了其对 DGP 的适用性。

3 深度高斯过程后验分析

在变分推理上采用一种新的推理方法是由 VI 对后验分布假设的限制形式所推动的。 变分假设是 $p(\{u{\}}_{l=l}^L|y)$ 采用多元高斯的形式，假设层之间是独立的。 虽然在单层模型中，后验的高斯近似被证明是正确的 [Williams and Rasmussen, 1996]，但对于 DGP，情况并非如此。

首先，我们用一个玩具问题来说明 DGP 中的后验分布可以是多峰的。 之后，我们提供证据表明我们在这项工作中考虑的每个回归数据集都会导致非高斯后验分布。

多模态玩具问题 两层 DGP$（L=2）$后验多模态在玩具问题上得到证明（表 1）。 为了演示的目的，我们做了 ${\sigma }^2=0$ 的简化假设，因此似然函数没有噪声。 这个玩具问题有两个最大后验 (MAP) 解决方案（模式 A 和模式 B）。 该表显示了 DSVI 在每一层的变分后验。 我们可以看到它随机匹配其中一种模式（取决于初始化），而完全忽略了另一种。 另一方面，诸如 SGHMC 之类的采样方法（在下一节中实现）探索了这两种模式，因此提供了更好的后验近似值。

经验证据：为了进一步支持我们关于后验多模态的主张，我们提供经验证据表明，对于现实世界的数据集，后验不是高斯的。

我们进行以下分析。考虑数据集下的后验是多元高斯分布的原假设。这个零假设意味着每个诱导输出的分布是高斯分布。我们使用下一节中描述的用于 DGP 的 SGHMC 实现来检查 SGHMC 为每个诱导输出生成的近似后验样本。为了得出 p 值，我们对高斯性应用峰度检验 [Cramer, 1998]。该检验通常用于识别多峰分布，因为这些分布通常具有显着更高的峰度（也称为 4 阶矩）。

对于每个数据集，我们计算 100 个随机选择的诱导输出的 p 值，并将结果与​​概率阈值 $\alpha =10^{-5}$ 进行比较。应用 Bonferroni 校正来解释大量并发假设检验。结果显示在图 1 的右侧。由于每个数据集的 p 值都低于阈值，因此我们可以 99% 确定所有这些数据集都具有非高斯后验。

4 深度高斯过程的基于采样的推理

与 VI 不同，当使用采样方法时，我们无法使用近似后验分布 $q(u)$ 来生成预测。相反，我们必须依赖从后验生成的近似样本，这些样本又可用于进行预测 [Dunlop et al., 2017, Hoffman, 2017]。

在实践中，运行一个包含两个阶段的采样过程。老化阶段用于确定模型和采样器的超参数。采样器的超参数使用启发式自动调整方法选择，而 DGP 的超参数使用新颖的移动窗口 MCEM 算法进行优化。

在采样阶段，采样器使用固定的超参数运行。由于连续样本高度相关，我们每 50 次迭代保存一个样本，并生成 200 个样本进行预测。一旦获得后验样本，就可以通过组合每个样本的预测来进行预测，以获得混合分布。请注意，使用此采样器进行预测并不比在 DSVI 中更昂贵，因为 DSVI 需要对层输出进行采样以进行预测。

4.1 随机梯度哈密顿量蒙特卡罗

SGHMC [Chen et al., 2014] 是一种马尔可夫链蒙特卡罗采样方法 [Neal, 1993]，用于从纯粹来自随机梯度估计的诱导输出 $p(u|y)$ 的难以处理的后验分布中生成样本。

随着辅助变量 $r$ 的引入，采样过程提供来自联合分布 $p(u,r|y)$ 的样本。 描述 MCMC 过程的方程可能与哈密顿动力学有关 [Brooks et al., 2011, Neal, 1993]。 负对数后验 $U(u)$ 充当势能，$r$ 充当动能：

在 HMC 中，运动的精确描述需要在每个更新步骤中计算梯度 $▽U(u)$，这对于大型数据集是不切实际的，因为将层输出集成到等式 2 中的成本很高。 这个积分可以用一个可以通过蒙特卡洛采样评估的下限来近似 [Salimbeni and Deisenroth, 2017]：

其中 ，$f^i$ 是来自层输出预测分布的蒙特卡洛样本：$f^i$~ $p(f|u)={\prod }_{l=1}^{L}p(f_l|u_l,f_{l-1})$。 这导致我们可以用来近似梯度的估计:

由于$▽rU(u)=-▽logp(u|y)=-▽logp(u,y)$，我们可以使用它来近似梯度。 陈等人 [2014]表明，如果使用以下更新方程，使用随机梯度估计（通过对数据进行二次采样获得）仍然可以进行近似后验采样：

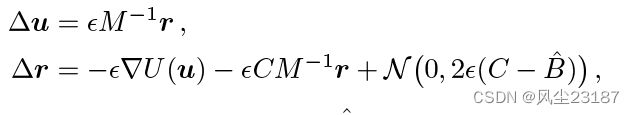
其中C是摩擦项，M是质量矩阵，$\hat{B}$是Fisher信息矩阵，$ϵ$ 是步长。 SGHMC 的一个警告是它有多个参数$（C、M、\hat{B}、ϵ）$，如果没有模型和数据的先验知识，很难设置这些参数。 我们使用 Springenberg 等人的自动调整方法。 [2016] 设置这些参数，这些参数已被证明适用于贝叶斯神经网络 (BNN)。 DGP 和 BNN 的相似性质强烈表明相同的方法适用于 DGP。

4.2 移动窗口马尔可夫链期望最大化

优化超参数（协方差函数的参数，诱导似然函数的输入和参数）证明对于 MCMC 方法很困难 [Turner and Sahani, 2011]。 简单的方法包括随着采样器的进展而优化它们，因为随后的样本高度相关，因此，超参数只是适合这种移动的后验点估计。

蒙特卡洛期望最大化 (MCEM) [Wei and Tanner, 1990] 是期望最大化算法的自然扩展，它与后验样本一起使用以获得超参数的最大似然估计。 MCEM 在两个步骤之间交替。 来自后验的 E-step 样本和 M-step 最大化样本和数据的平均对数联合概率：


然而，MCEM 有一个明显的缺点：如果 $M$ 步中使用的样本数量 ￥m$ 太少，那么超参数可能会过拟合这些样本。另一方面，如果 $m$ 太高，则 M-step 变得太昂贵而无法计算。此外，在 M-step 中，通过梯度上升最大化，这意味着计算成本随 $m$ 线性增加。

为了解决这个问题，我们引入了一种新的 $MCEM$ 扩展，称为移动窗口 MCEM。我们的方法以与先前描述的朴素方法相同的成本优化超参数，同时避免了其过拟合问题。

移动窗口 MCEM 背后的想法是将 E 和 M 步骤交织在一起。我们不是生成新样本然后最大化 $Q(\theta )$ 直到收敛，而是维护一组样本并朝着 $Q((\theta )$ 的最大值迈出一小步。在 E-step 中，我们生成一个新样本并将其添加到集合中，同时丢弃最旧的样本（因此是移动窗口）。接下来是 M 步，在该步中，我们从集合中随机抽取一个样本，并使用它对 $Q((\theta )$ 的最大值进行近似梯度步长。图 3 左侧的算法 1 显示了移动窗口 MCEM 的伪代码。

与 MCEM 相比，有两个优点。首先，超参数每次更新的成本是恒定的，并且不随 m 缩放，因为它只需要一个样本。其次，移动窗口 MCEM 的收敛速度比 MCEM 快。
图 3 的中间图证明了这一点。 MCEM 迭代地拟合一组特定后验样本的超参数。由于超参数和后验样本高度耦合，这种交替更新方案收敛缓慢 [Neath et al., 2013]。为了缓解这个问题，移动窗口 MCEM 通过在每个梯度步骤后生成一个新样本来不断更新其样本群。为了生成图 3 中心的图，我们绘制了测试集上的预测对数似然与算法迭代次数的关系，以展示移动窗口 MCEM 优于 MCEM 的卓越性能。对于 MCEM，我们使用了 m = 10 的集合大小（更大的 m 会减慢方法），我们生成了 500 多个 MCMC 步骤。对于移动窗口 MCEM，我们使用的窗口大小为 m = 300。本实验中使用的模型是一个 具有一个隐藏层的DGP，在 kin8nm 数据集上训练。

5 解耦的深度高斯过程

6实验

我们在 9 个 UCI benchmark 数据集上进行了实验2，范围从小（500 个数据点）到大（500,000 个），以便与基线进行公平比较。 在每个回归任务中，我们测量了平均测试对数似然 (MLL) 并比较了结果。 图 4 显示了 MLL 值及其超过 10 次重复的标准偏差。

根据 Salimbeni 和 Deisenroth [2017]，在所有模型中，我们将学习率设置为默认 0.01，小批量大小设置为 10,000，迭代次数设置为 20,000。 一次迭代涉及从窗口中抽取样本并通过梯度下降更新超参数，如图 3 左侧的算法 1 所示。深度从 0 个隐藏层到 4 个隐藏层不等，每层有 10 个节点。 协方差函数是标准平方指数函数，每个维度具有单独的长度尺度。 我们进行了随机的 0.8-0.2 训练测试拆分。 在 year 数据集中，我们使用固定的训练测试拆分来避免“制作人效应”，确保给定艺术家的歌曲不会同时出现在训练和测试集中。

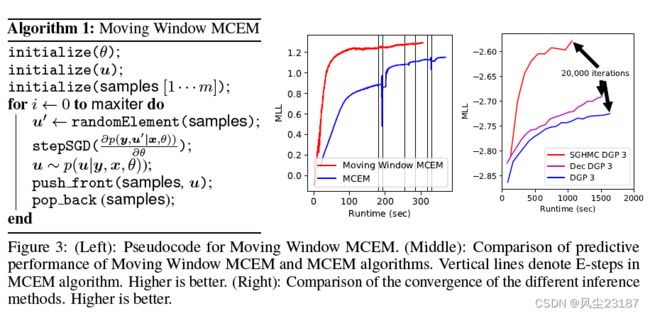
图 3：（左）：移动窗口 MCEM 的伪代码。 （中）：移动窗口 MCEM 和 MCEM 算法的预测性能比较。 垂直线表示 MCEM 算法中的 E 步。 越高越好。 （右）：不同推理方法的收敛性比较。 越高越好

基线：我们实验的主要基线是双重随机 DGP。 为了进行公平的比较，我们使用了与原始论文中相同的参数。 就诱导点的数量而言（诱导输入总是在潜在维度上共享），我们测试了两种变体。 首先，原始的耦合版本，每层 M = 100 个诱导点 (DGP)。 其次，解耦版本 (Dec DGP)，平均值为 Ma = 300，方差为 Mb = 50。选择这些数字是为了使单次迭代的运行时间与耦合版本相同。 进一步的基线由耦合（SGP：M = 100）和解耦（Dec SGP：Ma = 300，Mb = 50）单层 GP 提供。 最终基线是具有三个隐藏层和每层 50 个节点的稳健贝叶斯神经网络 (BNN) [Springenberg 等人，2016 年]。

SGHMC DGP（这项工作）：该模型的架构与基线模型相同。 M = 100 个诱导输入用于与基线保持一致。 老化阶段包括 20,000 次迭代，随后是采样阶段，在此期间，在 10,000 次迭代过程中抽取了 200 个样本。

MNIST 分类 ： SGHMC 在分类问题上也很有效。 使用 Robust-Max [Hern´andez-Lobato et al., 2011] 似然函数，我们将模型应用于 MNIST 数据集。 SGP 和 Dec SGP 模型分别达到了 96.8 % 和 97.7 % 的准确率。 关于深度模型，表现最好的模型是 12 月 DGP 3，达到 98.1%，其次是 SGHMC DGP 3，达到 98.0%，DGP 3 达到 97.8%。 [Salimbeni and Deisenroth, 2017] 报告 DGP 3 的值略高，为 98.11%。这种差异可归因于参数的不同初始化。

哈佛清洁能源项目： 该回归数据集是为哈佛清洁能源项目制作的 [Hachmann et al., 2011]。 它测量有机光伏分子的效率。 它是一个高维数据集（60,000 个数据点和 512 个二进制特征），已知可以从深度模型中受益。 SGHMC DGP 5 建立了新的最先进的预测性能，测试 MLL 为 -0.83。 DGP 2-5 达到 -1:25。 该数据集上的其他可用结果是具有期望传播的 DGPs的-0.99 和 BNN 的 -1.37 [Bui et al., 2016]。

运行时间： 为了支持我们的说法，即 SGHMC 的计算成本低于 DSVI，我们在蛋白质数据集的训练过程中绘制了不同阶段的测试 MLL（图 3 中的右图）。 与 DSVI 相比，SGHMC 收敛速度更快且限制更高。 SGHMC 以 1:6 倍的速度达到了 20,000 次迭代的目标。

7 结论

本文描述并展示了一种新的 DGP 推理方法 SGHMC，该方法从通常的诱导点框架中的后验分布中采样。 我们描述了一种新颖的移动窗口 MCEM 算法，该算法能够以快速有效的方式优化超参数。 这以降低的计算成本显着提高了中大型数据集的性能，从而为 DGP 中的推理建立了新的最新技术。