【每日一题】花期内花的数目+【差分数组】+【二分枚举】

Tag

【差分数组】【二分查找】【数组】【2023-09-28】

---

题目来源

2251. 花期内花的数目

---

题目解读

每朵花都有自己的花期，有些花的花期会有重叠，也就是说某些时刻会有多朵花同时开放，你需要找出在某些时刻花开的数量。

---

解题思路

解题的思路其实很明确，即确定某个时刻花开的数目即可。朴素的想法就是枚举的花，根据所有花的花期更新所有的时间点的花开数目。这种方法的最坏时间复杂度为 O(n^2)，$n$ 为数组 flowers 的长度，由于本题的数据规模达到 $10^5$，因此朴素方法一定超时。

方法一：差分数组

我们维护一个有序哈希表 cnts，表示某个时刻花开的数量（有序哈希表根据时间节点升序排序），我们枚举数组 flowers 中的每朵花 flower：

• 将花期的开始位置时刻（花开的时刻）的花开数量加一，即 ++cnts[flower[0]]；
• 将花期的开始位置时刻的下一时刻（花谢的下一个时刻）的花开数量减一，即 --cnts[flowers[1] + 1]。

我们对 flowers 中的每朵花都进行以上操作来更新 cnts。

为什么这样更新 cnts？因为这样，我们累加 cnts 的某个时刻的花开数量，即可得到某个时刻的所有花开数量。

我们以上更新的只是两种时刻的花开数量，即花开的时刻和花谢的下一个时刻，其他时刻的花开数量没有更新。因为我们只需要关注 “观赏者” 赏花的时刻，因此将 cnts 中没有覆盖到的观赏者赏花的时刻的花开数量进行更新。通过以下代码进行更新：

for (auto preson : presons) {
	cnts[x]; // cnts 中没有键 x，就 cnts[x] = 0；否则不进行任何操作
}

然后，我们更新 cnts：

int t = 0;
	for(auto &cnt : cnts){
		cnt.second = (t += cnt.second);
 }

t 表示当前花开的数目，这里我们利用的是差分数组的性质累加得到某个时刻花开的数目。

最后，输出对应时刻的花开数目到答案数组 res 中，并返回。

图解 cnts 的更新

现在以 示例 1 为例，来对以上的思路进行示例分析。

（1）flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]；

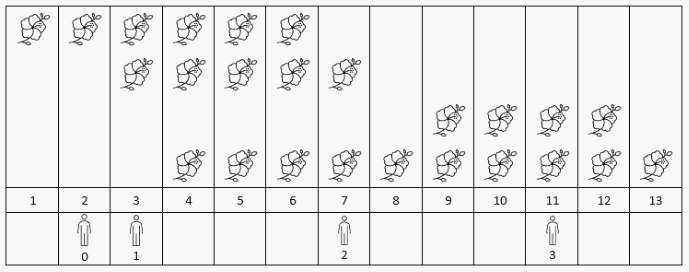
（2）遍历数组 flowers，更新得到的 cnts 如下图所示：

（3）将 cnts 中没有覆盖到的观赏者赏花的时刻的花开数量进行更新：

（4）最后累加更新 cnts。

实现代码

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& persons) {
        map<int, int> cnts;   // 统计每个时刻有几朵花开
        for(auto &it : flowers){
            ++cnts[it[0]];
            --cnts[it[1]+1];
        }
        for(auto x : persons){
            cnts[x];  // 没有 cnts[x] 就设置 cnts[x] = 0；否则不用管
        }

        int t = 0;
        for(auto &cnt : cnts){
            cnt.second = (t += cnt.second);
        }

        vector<int> ret;
        for(auto &x : persons){
            ret.push_back(cnts[x]);
        }
        return ret;
    }
};

复杂度分析

时间复杂度：$O(nlogn+mlogm)$，$n$ 为数组 flowers 的长度。cnts 是有序哈希表，每次插入的时间为 $O(logn)$，一共插入 n 个元素，构建有序集合的时间为 $O(nlogn)$。$m$ 为数组 presons 的长度，插入 m 个元素到有序哈希表中的时间复杂度为 $O(mlogm)$。

空间复杂度：$O(n+m)$。

方法二：二分查找

设：第 i 个人到达的时间为 presons[i]，在 presons[i] 时间点之前的花开数目为 x，在 presons[i] 时间点之前的花谢的数目为 y。则，presons[i] 时间点还处于开花状态的花数目为 x - y。

x 即为 start <= presons[i] 的花朵数目，y 即为 end < presons[i] 的花朵数目。

根据以上的分析，我们可以单独统计起始时间 start 和 结束时间 end，利用二分查找快速查找结果：

• 首先，将所有的 start 和 end 进行升序排序；
• 利用二分查找到 $star{t}_i<=persons[i]$ 的花朵数目 x，利用二分查找到 $en{d}_i<=persons[i]$ 的花朵数目 y，则第 i 个人可以看到的花朵数目为 x - y；
• 依次遍历并统计每个人的查询结果。

实现代码

class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& flowers, vector<int>& people) {
        vector<int> start, end;
        for (auto flower : flowers) {
            start.push_back(flower[0]);
            end.push_back(flower[1]);
        }

        sort(start.begin(), start.end());
        sort(end.begin(), end.end());

        int m = people.size();
        vector<int> res(m);

        for(int i = 0; i < n; ++i) {
            int x = upper_bound(start.begin(), start.end(), people[i]) - start.begin();
            int y = lower_bound(end.begin(), end.end(), people[i]) - end.begin();
            res[i] = x - y; 
        }
        return res;
    }
};

复杂度分析

时间复杂度：$O((n+m)logn)$，$n$ 为数组 flowers 的长度，$m$ 为数组 presons 的长度。对 start，end 排序的时间复杂度为 $O(nlogn)$；对每个人进行二分查找的时间为 $O(logn)$，有 m 个人，因此二分查找总时间复杂度为 $O(mlogn)$；所以总的时间复杂度为 $O((n+m)logn)$。

空间复杂度：$O(n)$，使用的额外空间为 start 和 end 数组，这两个数组排序使用的额外空间为 $O(logn)$，因此总的空间复杂度为 $O(n)+O(logn)=O(n)$。

---

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 哦。