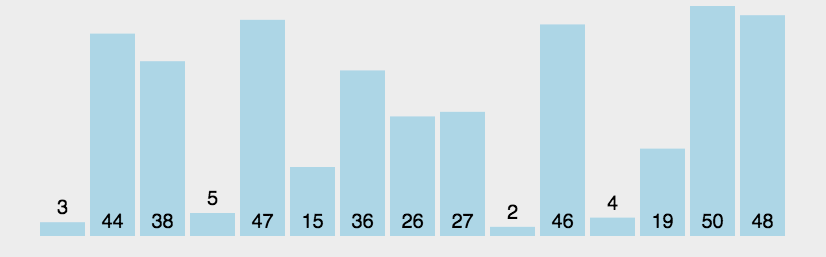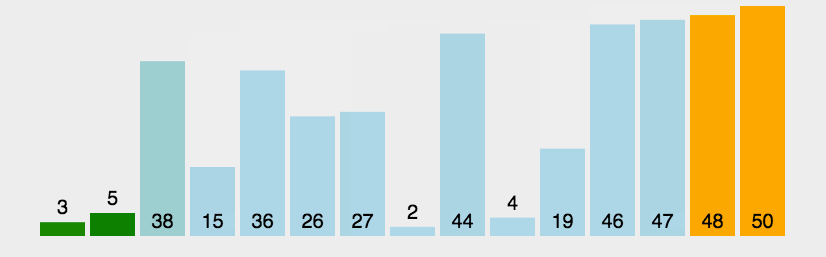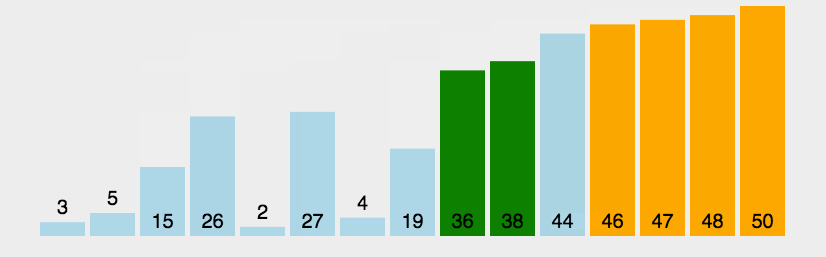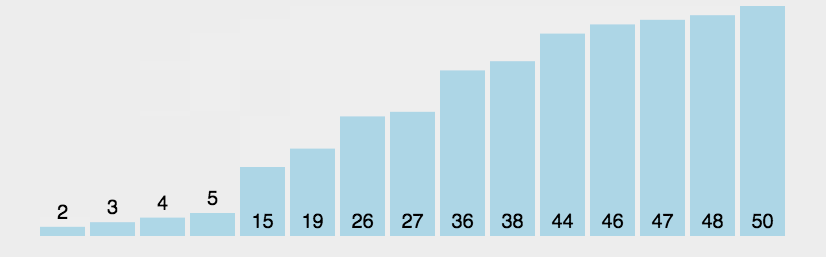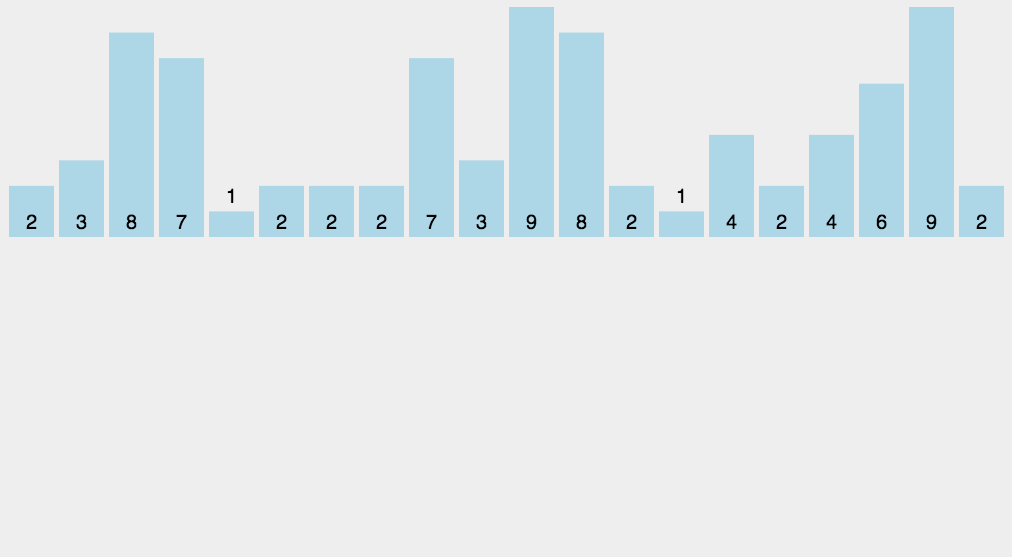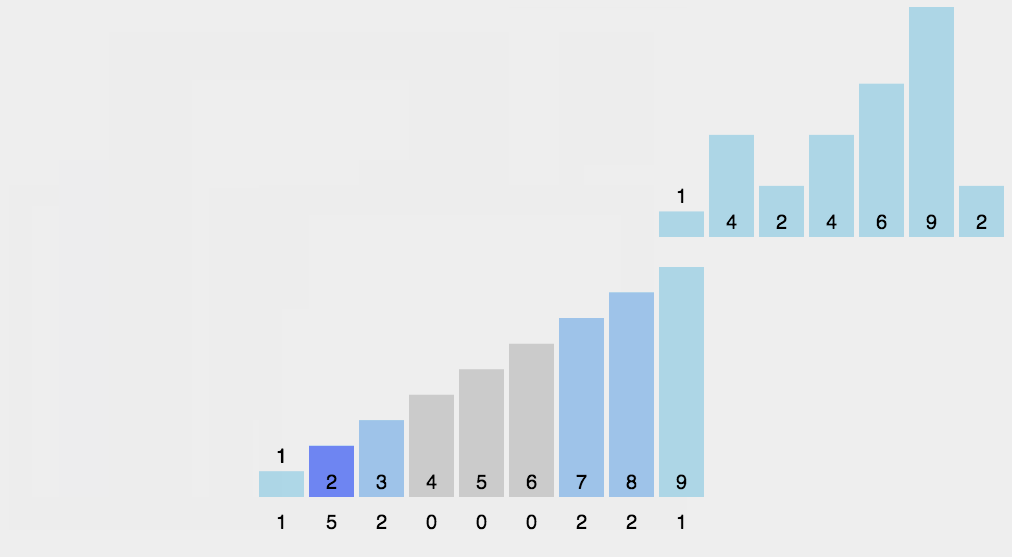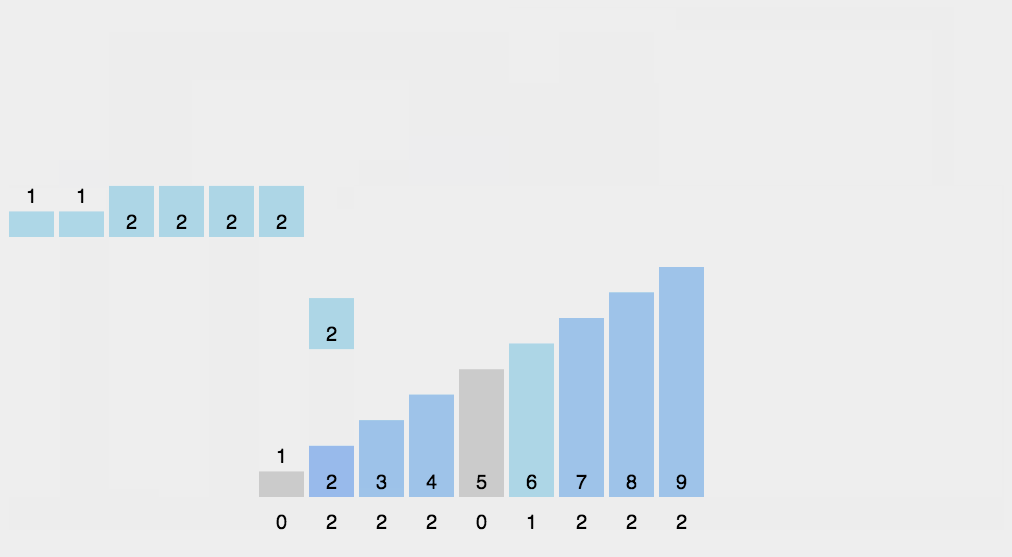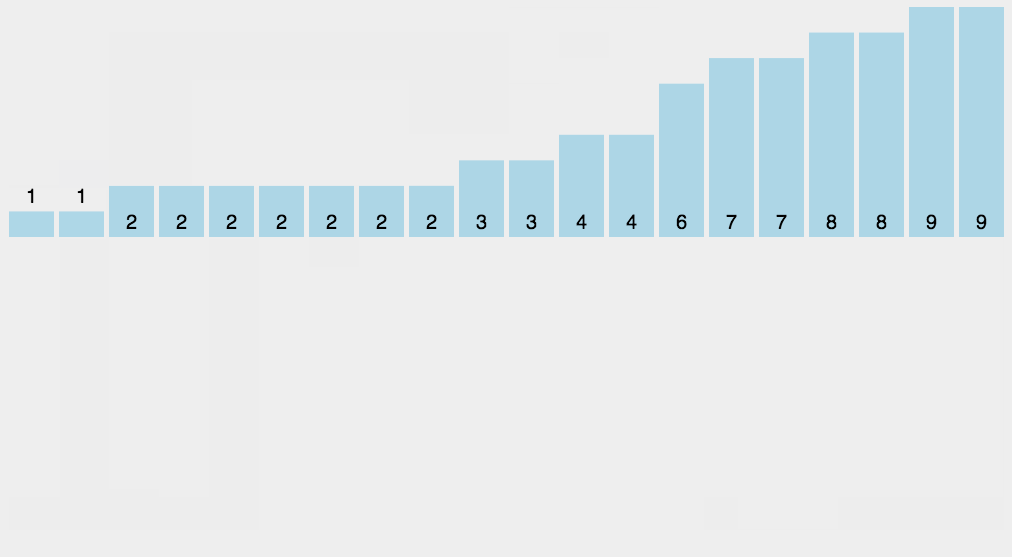关于『基本算法』:常见八大排序

序言

  基本算法向你发起进攻，请注意防守。

---

排序，是非常重要的内容，一般来说，我们经常用到的其实是十大排序——

分类		名称	时间复杂度			空间复杂度	稳定性
			平  均  情  况	最  好  情  况	最  坏  情  况	辅  助  存  储
比较类	插入排序	直接插入排序	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	稳定
		希尔排序	$O(n^{3\over 2})$	$O(n)$	$O(n^2)$	$O(1)$	不稳定
	选择排序	直接选择排序	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	不稳定
		堆排序	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(1)$	不稳定
	交换排序	冒泡排序	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	稳定
		快速排序	$O(n\log n)$	$O(n\log n)$	$O(n^2)$	$O(\log n)$	不稳定
	归并排序		$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$	稳定
非比较类	计数排序		$O(n+k)$	$O(n+k)$	$O(n+k)$	$O(max(n,k))$	稳定
	基数排序		$O(n*k)$	$O(n*k)$	$O(n*k)$	$O(n*k)$	稳定
	桶排序		$O(n+k)$	$O(n+k)$	$O(n^2)$	$O(n+k)$	稳定

注：在基数排序的复杂度中，$k$ 为位数，在另两个中为数据范围。

入学手册 ~

---

一、分类

1. 内部排序和外部排序

内部排序： 待排序记录存放在内存中进行的排序过程。
外部排序：待排序记录的数量很大，以致于内存不能一次容纳全部记录，所以在排序过程中需要对外存进行访问的排序过程。

2. 比较类排序和非比较排序

比较类排序： 通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 $O(n\log n)$，因此也称为非线性时间比较类排序。
非比较类排序： 不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

二、复杂度分析，算法稳定性和自适应

稳定： 如果 $a$ 原本在 $b$ 前面，而 $a=b$，排序之后 $a$ 仍然在 $b$ 的前面。
不稳定： 如果 $a$ 原本在 $b$ 的前面，而 $a=b$，排序之后 $a$ 可能会出现在 $b$ 的后面。
时间复杂度： 对排序数据的总的操作次数。反映当数据规模变化时，操作次数呈现什么规律。
空间复杂度： 是指算法在计算机内执行时所需存储空间的度量， 即个算法空间辅助空间单元的个数，与问题的规模没有关系。
自适应：当一些特殊数据出现时，算法与数据相适应，表现出不同特性与时间复杂度的过程。

三、名词解释：

$n$：数据规模。
$k$："桶"的个数。
算法复杂度：是用来衡量算法运行所需要的计算机资源（时间、空间）的量。

四、如何选择排序算法

1. 选择排序算法准则：

  每种排序算法都各有优缺点。因此，在实用时需根据不同情况适当选用，甚至可以将多种方法结合起来使用。

2. 选择排序算法的依据:

  影响排序的因素有很多，一般而言，需要考虑的因素有以下四点：

1. 关键字数量大小；
2. 数据规模大小；
3. 关键字的结构及其分布情况；
4. 对排序稳定性的要求。

3. 选择排序算法的方法:

>>> 设待排序元素的个数为 $n$

(1) 当 $n$ 较大，则应采用时间复杂度为 $O(n\log n)$ 的排序方法：快速排序，堆排序，归并排序。

• 快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短，但不稳定。
• 堆排序：如果内存空间允许且要求稳定性的。
• 归并排序：如果内存空间允许且要求稳定性的。

(2) 当 $n$ 较大，内存空间允许，且要求稳定性 → 归并排序。

(3) 当 $n$ 较小，可采用直接插入或直接选择排序

• 直接插入排序：当元素分布有序，直接插入排序将大大减少比较次数和移动记录的次数。
• 直接选择排序 ：当元素分布有序，且不要求稳定性，可选择直接选择排序。

(4) 一般不使用或不直接使用传统的冒泡排序。

---

本篇 被开刀的小白鼠 题目：#2625. 常用排序法

一、插入排序 (Insertion Sort)

(一). 直接插入排序 (Straight Insertion Sort)

直接插入排序，是最简单一种的排序方法。

1.基本思想:

  将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 $1$ 的有序表。
  即：先将序列的第 $1$ 个记录看成是一个有序的子序列，然后从第 $2$ 个记录逐个进行插入，直至整个序列有序为止。

2. 讨论：

$\text{Part1}$ 插入排序的使用场景

  虽然它是最坏时间复杂度为 $O(n^2)$ 基本排序算法之一，但插入排序常用于当数据近乎有序（因为它自适应，越接近有序越快）或问题规模很小时（因为它具有较低的代价）。
  由于这些原因，且它也很稳定，所以插入排序常常被使用（当问题规模较小时），而像递归（当问题规模较大时）常使用更高代价的分治排序，例如归并排序或快速排序。

3. 特性

• 稳定的。
• 空间复杂度：$O(1)$。
• 时间复杂度：$O(n^2)$ （比较和交换）。
• 自适应：越接近有序越快（最好情况为常数阶$O(n)$）。
• 非常低的代价。

4.动画演示:

5.函数原型

// Straight Insertion Sort
void Insert_sort(int *a, int n) {
	for (int i = 2; i <= n; i++) {
		t = a[i]; // 存储待排序元素  
		int j = i - 1; // 从前一个元素开始遍历
		while (t < a[j] && j) { // 查找在有序表的插入位置
			a[j + 1] = a[j];  // 元素后移  
			j--;
		}
		a[j + 1] = t; // 插入到正确位置  
	}
}

  在其实现过程中使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

---

(二). 希尔排序 (Shell Sort)

  希尔排序是直接插入排序算法的一种更高效的改进版本，该方法因 D.L.Shell 于 $1959$ 年提出而得名。

1.基本思想:

  希尔排序是基于插入排序的以下两点性质而提出改进方法的：

1. 插入排序在对几乎已经排好序的数据操作时，可以达到线性排序的效率（效率高）；
2. 但插入排序一般是低效的，因为插入排序每次只能将数据移动一位。

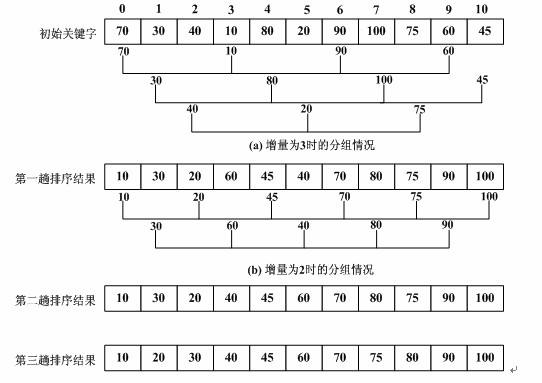
  希尔排序是把记录按下标的一定增量（即步长）分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键字越来越多，当增量减至 $1$ 时，希尔排序退化为直接插入排序，保证最终数列已有序，整个文件恰被分成一组，算法便终止。

2. 讨论：

$\text{Part1}$ 希尔排序的诞生与本质

  D.L.shell 于 $1959$ 年在以他名字命名的排序算法中实现了这一思想。算法先将要排序的一组数按某个增量 $d$ 分成若干组，每组中记录的下标相差 $d$。对每组中全部元素进行排序，然后再用一个较小的增量对它进行分组，在每组中再进行排序。当增量减到1时，整个要排序的数被分成一组，排序完成。
  一般的初次取序列的一半为增量，以后每次减半，直到增量为 $1$。
  该方法实质上是一种分组插入方法。比较相隔增量个位置的数，使得数移动时能跨过多个元素，则进行一次比较就可能消除多个元素交换。

$\text{Part2}$ 适用场景

  由于其低代价、相对简单的实现、自适应特性和 $O(n^{\frac{3}{2}})$ 的时间复杂度，它适用于中等大小的排序数据规模。

$\text{Part3}$ 补充拓展

真 · 一个奇怪的小知识~

  希尔排序的最坏情况时间复杂度其实取决于增量序列。
  对于一个增量序列 {1, 4, 13, 40, 121…}，时间复杂度为 $O(n^{\frac{3}{2}})$。
  对于其他增量序列，已知时间复杂度为 $O(n^{\frac{4}{3}})$ 甚至 $O(n\log n)$。
  现目前，我们既不知道时间复杂度的严格上限，也不知道最佳增量序列。

3. 特性

• 不稳定。
• 空间复杂度：$O(1)$。
• 时间复杂度：$O(n^{\frac{3}{2}})$ 。
• 越接近有序越快（最好情况为$O(n\log n)$）（有待再次考证）。

4.动画演示:

图解：

5.函数原型

// Shell Sort
void swap(int &x, int &y) { // swap函数简单版原型
	int t = x;
	x = y;
	y = t; 
}
void Shell_sort(int *a, int n) {
    int step; // 增量，即步长
    for (step = n / 2; step >= 1; step /= 2) { // 增量每次减半
        for (int i = step + 1; i <= n; i++) { // 从与第一位相隔增量个位置的数开始排序（即下标相隔一个step的位置）
            int tmp = i; // 分组排序指标
            while (tmp - step >= 1 && a[tmp - step] > a[tmp]) { // 比较相隔增量个位置的数的大小
                swap(a[tmp - step], a[tmp]);
                tmp -= step; // 指标向前挪移增量位
            }
        }
    }
}

真 · 一个奇怪的小知识~

  因为希尔排序是基于插入排序而改进得到的，所以希尔排序继承了插入排序的自适应特性。这种适应并不那么引人注目，因为希尔排序需要为每个增量遍历一次数据，但这种特性很重要。

---

二、选择排序 $(SelectionSort)$

(一). 直接选择排序 $\text{(Straight Selection Sort)}$

  直接选择排序，可以说是相当暴力的排序方法了。

1.基本思想:

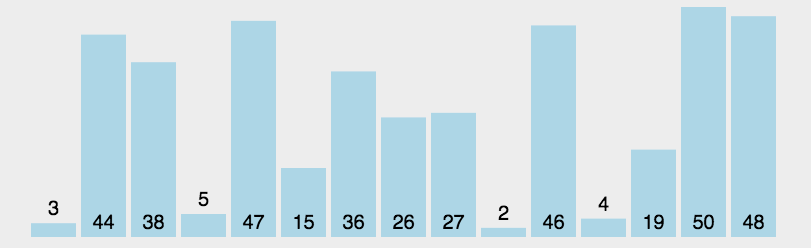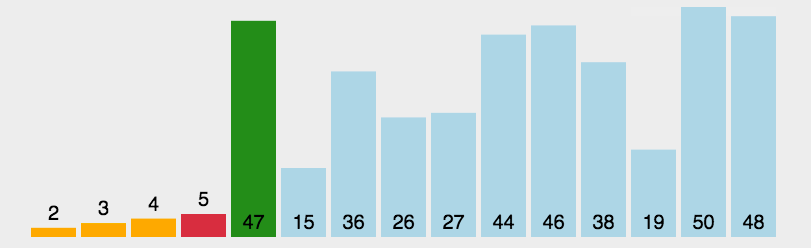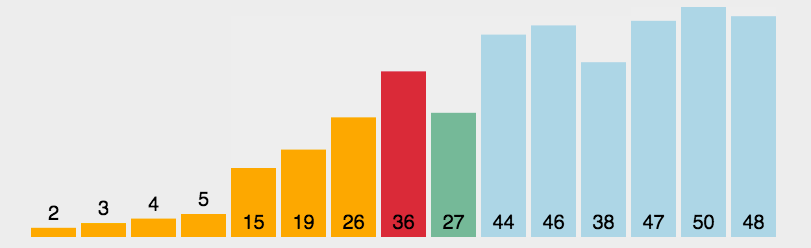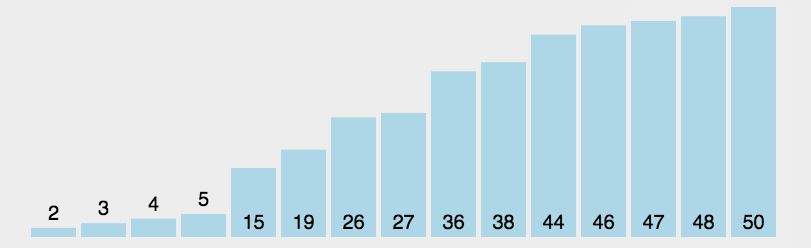
  在要排序的一组数中，选出最值与第一个位置数交换；然后在剩下的数当中再找最值与第二个位置数交换，依次类推，直到全部待排序的数据元素排完。

2. 讨论：

$\text{Part1}$ 永远不要使用选择排序

  从这里提供的比较中，大家可能会得出结论：「永远不要使用选择排序」。
  因为它不会以任何方式适应数据，不论数组是否有序都会执行原步骤。其时间复杂度始终是 $O(n^2)$ 。
  然而，选择排序具有最小化交换次数的特性。在交换位置频率很高的应用程序中，选择排序可能是较好的算法。

3. 特性

• 不稳定。
• 空间复杂度：$O(1)$ 额外空间。
• 时间复杂度：$O(n^2)$ （比较）。
• 自适应：不适应。

4.动画演示:

5.函数原型

// Straight Select Sort
void swap(int &x, int &y) { // swap函数简单版原型
	int t = x;
	x = y;
	y = t; 
}
void Select_sort(int *a, int n) {
	int minn, min_i;
    for (int i = 1; i <= n; i++) {
    	minn = a[i];
    	min_i = i;
   		for (int j = i + 1; j <= n; j++) {
   			if (a[j] < minn) {
   				minn = a[j];	
   				min_i = j;
			}	
		}
		swap(a[i], a[min_i]);
    } 
}

注：直接选择排序思考非常好理解，但是效率不是很好，所以一般不建议使用。

---

(二). 堆排序 $\text{(Heap Sort)}$

堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点

1.基本思想:

  将无序序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆。将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端。重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序

 >>> 因此，实现堆排序需解决两个问题：

1. 如何将 $n$ 个待排序的数建成堆；
2. 输出堆顶元素后，怎样调整剩余 $(n-1)$ 个元素，使其成为一个新堆。
   
   

2. 讨论：

$\text{Part1}$ 堆排的空间及时间复杂度

  堆排序执行 $O(n\log n)$ 就地排序，但不稳定。此外，堆排序不要任何辅助数组，只需要一个辅助变量，所占空间是常数，与 $n$ 无关，所以空间复杂度为O(1)

$\text{Part2}$ 关于大小顶堆

真 · 一个奇怪的小知识~

  堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

–>大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；

–>小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余 $(n-1)$ 个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了（升序排列）

3. 特性

• 不稳定
• 空间复杂度：$O(1)$ 额外空间
• 时间复杂度：$O(n\log n)$ (每次遍历 $n$ 遍元素，一共遍历 $\log n$ 次)
• 自适应：不是很适应

4.动画演示:（就这张让我悟了）

5.函数原型

// Heap Sort
void swap(int &x, int &y) {
	int t = x;
	x = y;
	y = t;
}
void sink(int *a, int i, int n) { // 把堆调整成大顶堆
    int l = 2 * i, r = l + 1, maxn;
    if (l > n) return ; // 没有左孩子时返回
    maxn = (r > n) ? l : (a[l] > a[r]) ? l : r; // 提取左右孩子的最大值位置
    if (a[i] >= a[maxn]) return ; // 符合大顶堆规则返回
    swap(a[i], a[maxn]); // 否则将最大值交换到父节点
    sink(a, maxn, n); // 向下调整
    return ;
}
void Heapsort(int *a, int n) {
    // heapify：初始堆
    for (int i = n / 2; i >= 1; i--) {
        sink(a, i, n); // 将数组放入堆顺序
    }
    // sortdown：将最大值“沉”到堆底
    for (int i = 1; i <= n; i++) { // 反复提取最大值并恢复堆顺序
        swap(a[1], a[n - i + 1]); // 将根结点（最大值）交换到末尾
        sink(a, 1, n - i); // 调整堆
    }
    return;
}

妈沫儿我悟了！！1

真 · 又一个奇怪的小知识~

Q：这个时间复杂度怎么推

A：1.构建初始堆复杂度：$O(n)$
   2.交换重建堆复杂度：$O(nlogn)$
   3.整个过程的复杂度：$O=O(n)+O(nlogn)=O(nlogn)$

注：本章鸣谢敬之大佬提供的帮助

---

三、交换排序 $(ExchangeSort)$

(一). 冒泡排序 $\text{(Bubble Sort)}$

冒泡排序，是一种计算机科学领域的较简单的排序算法，也是在下学会的第一个算法

1.基本思想:

1. 比较相邻的元素。如果第一个元素比第二个元素大（或小），就交换他们两个；
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。最后，尾元素应该会是最大（或最小）的数；
3. 重复以上步骤，直到数组有序。

真 · 一个奇怪的小知识~

  “冒泡排序” 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样，故名“冒泡排序”。

2. 讨论：

$\text{Part1}$  冒泡排序真的好慢！

  「冒泡排序」 是最慢的排序算法。其效率太低，是排序算法发展的初级阶段，实际应用中采用该算法的几率比较小。
  冒泡排序具有许多与插入排序相同的属性，但开销略高。在几乎排序的数据的情况下，冒泡排序需要 $O(n)$ 时间，但每个数据需要访问 $2$ 次（而插入排序更像是每个数据每遍访问 $1$ 次），因为在冒泡排序中，每个元素需要和左右两个元素进行比较，而插入排序却是直接与目标元素比较。

3. 特性

• 稳定的
• 空间复杂度：$O(1)$ 额外空间
• 时间复杂度：$O(n^2)$ （比较和交换）
• 自适应：越接近有序越快（最好情况为常数阶$O(n)$）

4.动画演示:

5.函数原型

// Bubble Sort
void swap(int &x, int &y) {
	int t = x;
	x = y;
	y = t;
}
void Bubble_sort(int *a, int n) {
	bool swapped = false;
    for (int i = 1; i < n; i++) {
    	for (int j = 1; j <= n - i; j++) {
    		if (a[j] > a[j + 1]) {
    			swap(a[j], a[j + 1]);
    			swapped = true;
			}
		}
		if (!swapped) break;
    } 
}

6.改进

由于冒泡排序实在是太效率低下（tm慢死）了，在这里为各位介绍一种改进 （但其实也挺拉的）

鸡尾酒排序 $\text{(Cocktail Sort)}$

  鸡尾酒排序，又称双向冒泡排序、鸡尾酒搅拌排序、搅拌排序、涟漪排序、来回排序或快乐小时排序，是冒泡排序的一种变形。

1.基本思想:

  先找到最小的数字，放在第一位，再找到最大的数字放在最后一位。然后再找到第二小的数字放到第二位，再找到第二大的数字放到倒数第二位。以此类推，直到完成排序

算法描述如下：

1. 先对数组从左到右进行升序的冒泡排序，最大的元素去到最右端
2. 再对数组进行从右到左的降序的冒泡排序，最小的元素去到最左端
3. 以此类推，持续的、依次的改变冒泡的方向，并不断缩小没有排序的数组范围，直到元素全体有序。

2. 讨论：

$\text{Part1}$

  鸡尾酒排序是冒泡排序的一种改进，倒并未有本质的改变。与冒泡排序的时间复杂度和空间复杂度相近，整体的性能都比较差，比冒泡排序的效率稍微好一点，原因是冒泡排序只从一个方向进行比对(由低到高)，每次循环只移动一个项目。

3. 特性

• 稳定的
• 空间复杂度：$O(1)$ 额外空间（交换）
• 时间复杂度：$O(n^2)$
• 自适应：越接近有序越快（最好情况为常数阶$O(n)$）

4.函数原型

// Cocktail Sort 
void swap(int &x, int &y) {
	int t = x;
	x = y;
	y = t;
}
void Cocktail_sort(int *a, int n){
    bool sorted = false; // 双向同时进行
    for(int i = 1; i <= n / 2; i++) {
        sorted = false;
        // 升序排列
        for(int j = i; j <= n - i; j++) {
            if(a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
                sorted = true;
            }
        }
        // 降序排列
        for(int j = n - i; j >= i; j--) {
            if(a[j] < a[j - 1]) {
                swap(a[j], a[j - 1]);
                sorted = true;
            }
        }
        if(sorted == false) {
            break;
        }
    }
}

你学废了吗_(￣▽￣)

---

(二). 快速排序 $\text{(Quick Sort)}$

  快速排序是对冒泡排序算法的一种改进。

1.基本思想:

  快速排序算法通过多次比较和交换来实现排序，其排序流程（默认升序）如下：

1. 选定一个基准值(这里默认左边）；
2. 将大于或等于分界值的数据交换到数组右段，小于分界值的数据交换到数组的左段。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值，中间交界的地方就把基准值放上去；
3. 然后， 左边和右边的数据可以独立排序 。对于左侧和右侧的数组数据也做以上处理；
4. 重复上述过程（可以看出，这是一个递归定义）。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。

2. 讨论：

$\text{Part1}$ 关于快排

  快速排序是强大且代价低的（在阁下写对的前提下），当不需要稳定排序时，快速排序是最出色的通用排序之一

注：在快速排序中，3路分区版本更优，但2路分区（Hoare版本，快排发明者最初的写法）也是相当不错的

$\text{Part2}$ 关于时间复杂度

  2路分区（Hoare版本）表现出较差的局部性，并且关键的是，当数列中**基准值为最大值（或最小值）**时，它可能会表现出 $O(n^2)$ 的时间复杂度

$\text{Part3}$ 关于空间复杂度

  关于其空间复杂度，快速排序使用的空间的确是 $O(1)$ 的；而真正消耗空间的是递归调用，因为每次递归就要保持一些数据：最优的情况下空间复杂度为 $O(\log n)$，即每一次都平分数组的情况。最差的情况下空间复杂度为 $O(n)$，即退化为冒泡排序的情况

  由于两个子排序都是递归执行的，因此在递归不平衡的最坏情况下，快速排序需要 $O(n)$ 额外的递归堆栈空间。这种情况发生概率极小 (不亚于阁下在路上走着突然被“以刀劈狼首”，或者“数刀毙之”)，但可以通过先递归进行排序较小的子数组来避免；第二个子数组排序是尾递归调用，可以通过迭代来完成。通过这种优化，算法在最坏的情况下使用 $O(logn)$ 额外空间

  综上，平均空间复杂度为 $O(\log n)$

3. 特性

• 不稳定
• 空间复杂度：$O(\log n)$ 额外空间
• 时间复杂度：$O(n\log n)$ (每次遍历 $n$ 遍元素，一共遍历 $\log n$ 次)
• 自适应：不适应

4.动画演示:

5.函数原型

// Quick Sort
void Quick_sort(int *a, int begin, int end) {
    if (begin >= end) { 
        return;
    }
    int key = a[begin];      
    int l = begin, r = end;  
    while (l != r) {    
        while (a[r] > key && l < r) {  // 选左端做基准值，所以 r 指针先走            	    r--;
        }
        // 注：a[r] > key不写等于，使得遇到和 key相等的数会停下来；最后
        // key和相遇点交换的时候，原来相等的数的相对位置会改变，所以快速排序是不稳定的。
        while (a[l] <= key && l < r) {  
	    l++;
        }
        if (l < r) {           
            swap(a[l], a[r]);  
        }
    }
    swap(a[begin], a[l]);  // 将基准值与相遇点的值交换，基准值来到排好序后的正确位置。
    // 此时 l(r) 所在位置左侧的所有数都比基准值小，右侧的所有数都比基准值大。
    quick_sort(a, begin, l - 1);  // 分段递归排序
    quick_sort(a, l + 1, end);
}

真 · 又一个奇怪的小知识~

  “快速排序” 是递归的、速度最快的排序算法，但是在内存有限的情况下不是一个好的选择。而且，对于基本有序的数据序列排序，快速排序反而退化为冒泡排序，变得比较慢

  快排是软件工业中最常见的常规排序法（我爱快排！！1），其双向指针扫描和分区算法是核心，快排较于归并更重视子问题拆分

6.其他版本

快排版本还挺丰富的哈

(一). 挖坑法

1.基本思想:

1. 先将选定的基准值 (一般取最左边) 直接取出，然后留下一个「坑」；
2. 当右指针遇到小于基准值的数时，直接将该值放入「坑」中，而右指针指向的位置形成新的「坑位」，然后左指针遇到大于基准值的数时，将该值放入「坑」 中，左指针指向的位置形成「坑位」；
3. 重复该步骤，直到左右指针相遇；
4. 最后将基准值放入「坑位」之中，之后以基准值为界限，递归排序基准值左右区间。

2. 讨论：

$\text{Part1}$

  挖坑法其实和 2路分区 本质上是一样的，稍稍优于 2路分区 的是其可以避免交换，所以会快一些。

注：在实际测试中，2路分区总时间 $217\mathrm{ms}$，挖坑法 $193\mathrm{ms}$。

3. 特性

• 不稳定
• 空间复杂度：$O(\log n)$ 额外空间
• 时间复杂度：$O(n\log n)$ (每次遍历 $n$ 遍元素，一共遍历 $\log n$ 次)
• 自适应：不适应

4.动画演示:

5.函数原型

// 挖坑法
void Quick_sort(int *a, int l, int r) { // 挖坑法
    if (l >= r)
        return;
    int key = a[l]; 
    int i = l, j = r; 
    while (i < j) { 
        while (a[j] >= key && j > i) j--; 
        // 注：a[j] >= key一定要取等！！1
        // 否则当数据相等的较多时很浪费时间
        if (i < j) 
            a[i] = a[j];                   // 右指针成为新坑
        while (a[i] <= key && i < j) i++; 
        if (i < j)
            a[j] = a[i]; 
    }
    a[i] = key;  // 基准值放入该坑
    // 这个时候左指针走过的位置都是比 key 小的数，右指针走过的都是比 key 大的数，所以相遇点就是 key 该在的位置
    quick_sort(a, l, i - 1);  // 以基准值为界递归左右两段
    quick_sort(a, i + 1, r);
return;
}

(二). 快速排序三路分区 $\text{(Quick Sort 3-Way})$

1.基本思想:

1. 从最左侧开始，向右找到一个不小于基准值的数；
2. 从最右侧开始，向左找到一个不大于基准值的数；
3. 交换两个位置上的数；
4. 如果左元素和基准值相等，则交换到左端；
5. 如果右元素和基准值相等，则交换到右端；
6. 重复以上步骤，直到两指针相遇；
7. 将基准值交换到两指针相遇处，注意交换完成后数组最左侧不是基准值 ；
8. 将数组中左端等于基准值的数交换到中间 ；
9. 将数组中右端等于基准值的数交换到中间 ；
10. 继续递归左右子列。

2. 讨论：

$\text{Part1}$ 关于三路快排的产生

  快排是二路划分的算法。如果待排序列中重复元素过多，也会大大影响排序的性能。这时候，如果采用三路划分，则会很好的避免这个问题。
  如果一个待排序列重复元素过多，我们就选择一个基准值，设为 key，那么数列可以分为三部分：小于 key，等于 key，大于 key。
  等于 key 的部分就无需再参与后续的递归调用了，速度自然就大大提升了。

$\text{Part2}$ 关于三路快排的特性

  与标准的 $2$ 路分区版本相比，快速排序的 $3$ 路分区变体的开销略高。两者都具有相同的最佳、典型和最坏情况的时间界限，但此版本在待排序列中元素相同较多的情况下具有高度的适应性
  在 $2009$ 年，俄罗斯人 Vladimir Yaroslavskiy 发现了一种双枢轴 $3$ 路分区变体——Dual-Pivot QuickSort，它在理论上和实践上都优于单枢轴 $3$ 路分区方法。

3. 特性

• 不稳定。
• 空间复杂度：$O(\log n)$ 额外空间。
• 时间复杂度：$O(n\log n)$ (每次遍历 $n$ 遍元素，一共遍历 $\log n$ 次)。
• 自适应：不同元素越少越快（当只有唯一元素不同时 ，时间复杂度 $O(n)$）

4.动画演示:

5.函数原型

// Quick Sort 3-Way
void Quick3(int *a, int begin, int end) {
	if (begin >= end) { 
		return ;
	}
	int key = a[begin]; 
	int i = begin, j = end + 1, p = begin, q = end + 1; // i、j为指针，p、q用于将与 key 相同的值交换到数组两端
	while (i < j) {
		while (i < j && a[--j] > key) ; //自左向右扫描第一个不大于基准值的数
		while (i < j && a[++i] < key) ; //自右向左扫描第一个不小于基准值的数
		if (i < j) {
			swap(a[i], a[j]); //比基准值小的数放左边，比 基准值大的数放右边 
			if (a[i] == key) swap(a[i], a[++p]); //如果左元素和基准值相等，则交换到左端
			if (a[j] == key) swap(a[j], a[--q]); //如果右元素和基准值相等，则交换到右端
		}
	}
	swap(a[i], a[begin]); //将基准值交换到两指针相遇处,注意交换完成后数组最左侧不是基准值
	i--, j++; //将两指针分别放置在基准值的左右两侧，准备交换  
	for (int k = begin + 1; k <= p; k++, i--) swap(a[i], a[k]);  //将数组中左端等于基准值的数交换到中间 
    for (int k = end; k >= q; k--, j++) swap(a[j], a[k]);  //将数组中右端等于基准值的数交换到中间 
    //继续递归左右子列 
	Quick3(a, begin, i); 
	Quick3(a, j, end);
}

(三). 前后指针法

1. 基本思想

1. 先选一个基准值 key（本次演示取最左边为基准值，这里选右边的话操作略有不同）
2. prev 放在最左边，cur 在 prev 下一个位置
3. cur 往右找比 key 小的值，找到后让 prev 后移一位，并交换 prev 和 cur 所指位置上的数
4. 重复以上步骤，直到 cur 超出最右边，把基准值和 prev 所指位置上的数交换

2. 讨论：

$\text{Part1}$ 代码易错点

  从排序过程来看，prev 把比基准值大的数都拉到了右边，cur 把比基准值小的数都推到了左边

  这里注意：当 cur 找到比基准值小的数后， prev 要往后移一位再交换，交换后 cur 也要向后移一位

  有意思的是，交换后如果没有让 cur 后移一位，程序并不会死循环，因为每次交换prev 都会向后移，prev 会超过 cur 并越界让随机值和 cur 交换，使得 cur 又向后移动，当 cur 超出右边界循环就结束了（可以亲身体会一下）。

3. 特性

• 不稳定
• 空间复杂度：$O(\log n)$ 额外空间
• 时间复杂度：$O(n\log n)$ (每次遍历 $n$ 遍元素，一共遍历 $\log n$ 次)
• 自适应：不适应

4.动画演示:

5.函数原型

// 前后指针法
void Quicksort_zhizhen(int *a, int begin, int end) {
	if (begin >= end) { 
		return ;
	}
	int key = a[begin]; 
	int prev = begin, cur = begin + 1; 
	// prev:英文单词previous缩写
	// cur:英文单词current缩写
	while (cur <= end) { 
		while (a[cur] >= key && cur <= end) cur++;
		if (cur <= end && a[cur] < key) {
			prev++;
			swap(a[cur], a[prev]);
			cur++; // 一定要后移 
		}
	}
	swap(a[begin], a[prev]);
	Quicksort_zhizhen(a, begin, prev - 1); 
	Quicksort_zhizhen(a, prev + 1, end);
}

6. 效率对比

耗时测试：20组数据比较共同用时 $(N\le 100000)$

1. 快速排序（Hoare版本（快排发明者最初的写法），2路分区）：$217\mathrm{ms}$；
2. 挖坑法 ：$193\mathrm{ms}$；
3. 快速排序（3路分区）：$217\mathrm{ms}$；
4. 前后指针法 ：$201\mathrm{ms}$。

  挖坑法在这组数据中表现出人意料，居然是最快的，而且还在 $200\mathrm{ms}$ 以内（（震惊中。。。
  3路分区在数据重复较多的时候才会大放异彩，但在此处的数据中，并没有大量重复数据，所以时间和 2路分区 一样（想康康 3路分区 nb之处的童鞋可以找一些重复元素很多的数据 try try）；
  前后指针法作为一种比较新颖的算法表现还是不错，差一点点就挺进 200ms 以内了。

真 · 一个奇怪的小知识~

  “快速排序” 无法解决的缺陷：当数据全部相同，或少量不同数据交替出现，这两种情况下快排的效率很低，即使是 3路分区 也没办法解决

---

四、归并排序 $\text{(Merge Sort)}$

归并排序是建立在归并操作上的一种有效，稳定的排序算法

1.基本思想:

  将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

※ 主要思想：分治法

  在计算机科学中，分治法是一种很重要的算法。字面上的解释是 “分而治之” ，就是 把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题 分成更小的子问题 ，直到最后子问题可以简单的直接求解，原问题的 解即子问题的解的合并 。这个技巧是很多高效算法的基础

敲黑板 · 一个奇怪的小知识~

分治法的精髓：

分 --> 将问题分解为规模更小的子问题

治 --> 将这些规模更小的子问题逐个击破

合 --> 将已解决的子问题合并，最终得出“母”问题的解

2. 讨论：

$\text{Part1}$ 归并的优点

  归并排序速度仅次于快速排序，一般用于对总体无序，但是各子项相对有序的数列

  如果不考虑使用 $O(n)$ 额外空间，那么归并排序是一个很好的选择：它实现简单，并且是唯一稳定的 $O(n\log n)$ 排序算法。请注意，在对链表进行排序时，归并排序只需要 $O(\log n)$ 额外空间。

$\text{Part2}$ 使用场所

  归并排序是多种情况下的首选算法：1.需要稳定排序；2.对链表进行排序；3.随机访问比顺序访问成本高得多时。

$\text{Part3}$

真 · 一个奇怪的小知识~

  数据是要存在数组里面的，所以要开和数据量一样大的数组，即空间复杂度（使用数组）为 $O(n)$

  注：递归的时间复杂度看的是递归深度，因为同一层递归是可以使用同一块空间的（阁下可以整几道题 try try）

3. 特性

• 稳定的
• 空间复杂度：$O(n)$ 辅助数组的额外空间 / $O(\log n)$ 辅助链表的额外空间（用于递归）
• 时间复杂度：$O(n\log n)$ （每次都需要给 $n$ 个元素排序，排序的过程需要 $\log n$）
• 自适应：不适应(无论原始数组是否是有序的，都要递归分隔并向上归并排序，所以时间复杂度始终是$O(n\log n)$)
• 不需要随机访问数据
  
  

4.动画演示:

5.函数原型（似乎不太标准）

// Merge Sort
void Merge(int *a, int l, int mid, int r) {
	if (l >= r) return ; // 分到空集或只有一个元素，子问题为有序
	int i = l, j = mid + 1; // 定义左右子段的头指针
	int res[100005], len = 1; // 临时数组储存答案
	for (len; i <= mid && j <= r; len++) {
		if (a[i] <= a[j]) { // 若此处不取等则为不稳定排序
			res[len] = a[i++];	
		} else {
			res[len] = a[j++];
		} 
	}
	while (i <= mid) res[len++] = a[i++]; // 把剩余的元素顺次加在尾部
	while (j <= r) res[len++] = a[j++];
	len = 1;
	while (l <= r) a[l++] = res[len++]; // 把已经有序的子问题放回原数组中
	return ;
}
void Mergesort(int *a, int l, int r) {
	int mid;
	if (l < r) {
		mid = (l + r) >> 1;
		Mergesort(a, l, mid); // 分成子问题
		Mergesort(a, mid + 1, r);
		Merge(a, l, mid, r); // 把子问题的解合并起来
	}
	return ; 
}

真 · 一个奇怪的小知识~

  “归并排序” 相较于 “快速排序” 而言，归并更重视子问题的解的合并。归并排序其实是用空间换时间，它固然快，但所需付出的空间代价是较为昂贵的

---

五、计数排序 $\text{(Counting Sort)}$

计数排序是一个非基于比较的排序算法。

1.如果要排序的项目是小范围的整数，我们可以计算每个整数（在这个小范围内）的出现频率，然后通过循环该小范围来按排序顺序输出项目

2.计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用：统计相同元素出现次数，根据统计的结果将序列回收到原来的序列中

1.基本思想:

  计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于 $x$ 的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上

2. 讨论：

$\text{Part1}$ 计数的优势

  计数排序的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法

  当然这是一种牺牲空间换取时间的做法，而且当 $O(k)>O(n\log n)$ 的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是 $O(n\log n)$, 如归并排序，堆排序）

$\text{Part2}$ 非比较的稳定排序

  我们看到，计数排序算法没有用到元素间的比较，它利用元素的实际值来确定它们在输出数组中的位置。因此，计数排序算法不是一个基于比较的排序算法，从而它的计算时间下界不再是 $O(nlogn)$ 。另一方面，计数排序算法之所以能取得线性计算时间的上界是因为对元素的取值范围作了一定限制，即 $k=O(n)$ 。如果 $k=n^2,n^3,..$ ，就得不到线性时间的上界。经计数排序，输出序列中值相同的元素之间的相对次序与他们在输入序列中的相对次序相同，换句话说，计数排序算法是一个稳定的排序算法

$\text{Part3}$

真 · 一个奇怪的小知识~

  计数排序在数据范围集中时，效率很高，但是适用范围及场景有限，比如当数组最大和最小差值过大时，浮点数等等，但可以处理负数和字符

3. 特性

• 稳定的
• 空间复杂度：$O(max(n,k))$
• 时间复杂度：$O(n+k)$
• 自适应：不适应
• 局限性
  
  

4.动画演示:

5.函数原型

// Counting Sort
void Countingsort(int* a, int n) {
	int max = a[1], min = a[1];
	for (int i = 1; i <= n; i++) {
		if (a[i] > max) { // 寻找最大最小值，以方便定义计数数组范围
			max = a[i];
		}
		if (a[i] < min) {
			min = a[i];
		}
	}
	int range = max - min + 1; // 定义数组范围
	int count[range] = {}; // 创建关键值（计数）数组
	for (int i = 1; i <= n; i++) { // 遍历数组中的每个元素
		count[a[i] - min]++; // 以最小值为基准确定位置，相应的计数器增加1
	}
	int j = 0;
	for (int i = 0; i < range; i++) {
		while (count[i]--) { // 当计数为非零数时循环
			a[++j] = i + min; // 此时在对应位置，大小为差值加最小值（基准值），将计数减1
		}
	}
    return ;
}

真 · 一个奇怪的小知识~

  在最大值和最小值相差较小的情况下，计数排序的效率会达到排序的天花板$O(n)$

---

六、基数排序 $\text{(Radix Sort)}$

基数排序是一种分配式排序

1.如果要排序的项目是整数，范围大但位数少，我们可以合并计数排序用基数排序的想法来实现线性时间复杂度

2.基数排序又称“桶子法”或 $binsort$。
顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用。
在某些时候，基数排序法的效率高于其它的稳定性排序法

1.基本思想:

  基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串，所以基数排序也可以适用于字符

  基数排序就像在人工比较数的大小，是按位来对比的

  将所有待排序的数统一为相同的数位长度，数位较短的数前面补零，然后从低位到高位按位比较，位数字小的排在前面，大的排在后面，这样当比较第 $n$ 位时前 $n-1$ 位都是有序的，如此循环的比较，直到最高位比较完成，整个序列就是有序的了

2. 讨论：

$\text{Part1}$ 关于基数排序

  基数排序适用于规模很大的情况，但是只适用于整数的排序，如果对浮点数进行基数排序，则必须明确浮点数的存储格式，然后通过某种方式将其映射到整数上，最后再映射回去，过程复杂

  基数排序过程无须比较关键字，而是通过“分配”和“收集”过程来实现排序。它们的时间复杂度可达到线性阶：$O(n)$

  基数是按照优先级顺序排序。因为它基于分别排序，且分别收集，所以是稳定的

$\text{Part2}$ 如何按关键字存储

  基数排序一般借助桶式排序，每次按第 $n$ 位排序时，采用桶式排序。对于如何安排每次落入同一个桶中的数据有两种安排方法：

  1. 顺序存储：每次使用桶式排序，放入r个桶中，相同时增加计数

  2. 链式存储：每个桶通过一个静态队列来跟踪

$\text{Part3}$

敲黑板 · 一个奇怪的小知识~

  设 $n$ 个元素的待排序列包含 $d$ 个关键码 $\{k1，k2，\dots ，kd\}$，则称序列对关键码 $\{k1，k2，\dots ，kd\}$ 有序是指：对于序列中任两个记录 $r[i]$ 和 $r[j](1\le i\le j\le n)$ 都满足下列有序关系：

$(k_i^1,k_i^2,\cdots ,k_i^d)<(k_j^1,k_j^2,\cdots ,k_j^d)$

  其中 $k1$ 称为最主位关键码，$kd$ 称为最次位关键码

※ 两种多关键码排序方法：

  多关键码排序按照从最主位关键码到最次位关键码或从最次位到最主位关键码的顺序逐次排序，分两种方法：

最高位优先法 $(MostSignificantDigitfirst)$，简称 MSD 法：

1）先按 $k1$ 排序分组，将序列分成若干子序列，同一组序列的记录中，关键码 $k1$ 相等

2）再对各组按 $k2$ 排序分成子组，之后，对后面的关键码继续这样的排序分组，直到按最次位关键码 $kd$ 对各子组排序后

3）再将各组连接起来，便得到一个有序序列

最低位优先法 $(LeastSignificantDigitfirst)$，简称 LSD 法：

1）先从 $kd$ 开始排序，再对 $kd-1$ 进行排序，依次重复，直到按 $k1$ 排序分组分成最小的子序列

2) 最后将各个子序列连接起来，便可得到一个有序的序列

3. 特性

• 稳定的
• 空间复杂度：$O(n\ast k)$
• 时间复杂度：$O(n\ast k)$
• 自适应：不适应
  
  

4.动画演示:

5.函数原型

// Radix Sort - LSD法
void Radixsort(int* a, int n) {
	const int base = 10 + 5;
	struct node { // 这里是链式存储
		queue<int> q; // 每个桶通过一个静态队列来跟踪
	} bucket[base]; // 创建10个桶（队列）分别给每个数位（0~9）
	int maxn = 0, exp = 1;
	for (int i = 1; i <= n; i++) { 
		maxn = max(a[i], maxn); // 获取最大数以便找到最高位
	}
	while (maxn / exp != 0) { // 从最低位开始到最高位遍历
		for (int i = 1; i <= n; i++) { // 遍历数列中的每个元素
			bucket[a[i] / exp % 10].q.push(a[i]); // 将元素一直相应的桶中
		}
		int j = 1;
		for (int i = 0; i <= 9; i++) { // 从最低位开始
			while (!bucket[i].q.empty()) { // 当桶不是空的
				a[j++] = bucket[i].q.front(); // 将元素恢复至数列中
				bucket[i].q.pop();
			}
		}
		exp *= 10; // 下一位
	}
    return ;
}

真 · 一个奇怪的小知识~

  基数排序可以说是扩展了的桶式排序，比如当待排序列在一个很大的范围内，比如0到999999，此时用桶式排序是很浪费空间的。

  而基数排序把每个排序码拆成由d个排序码，比如任何一个6位数（不满六位前面补0）拆成6个排序码，分别是个位的、，十位的、，百位……排序时，分6次完成

---

七、桶排序 $\text{(Bucket Sort)}$

桶排序是鸽巢排序的一种归纳结果

桶排序又称“箱排序”。
是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间 $O(n)$。但桶排序并不是比较排序，他不受到 $O(n\log n)$ 下限的影响。

1.基本思想:

  桶排序是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素，通过映射函数，将待排序数组中的元素映射到各个对应的桶中，对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

  根据待排序集合中最大元素和最小元素的差值范围和映射规则，确定申请的桶个数；

  遍历待排序集合，将每一个元素移动到对应的桶中；
对每一个桶中元素进行排序，并移动到已排序集合中。

突然发现桶排不简单

2. 讨论：

$\text{Part1}$ 关于鸽巢排序

敲黑板 · 一个奇怪的小知识~

  鸽巢排序（Pigeonhole sort），也被称作基数分类，是一种时间复杂度为O(n)（大O符号）且在不可避免遍历每一个元素并且排序的情况下效率最好的一种排序算法。但它只有在差值（或者可被映射在差值）很小的范围内的数值排序的情况下实用。
当涉及到多个不相等的元素，且将这些元素放在同一个"鸽巢"的时候，算法的效率会有所降低。为了简便和保持鸽巢排序在适应不同的情况，比如两个在同一个存储桶中结束的元素必然相等
我们一般很少使用鸽巢排序，因为它很少可以在灵活性，简便性，尤是速度上超过其他排序算法。事实上，桶排序较鸽巢排序更加的实用。

$\text{Part2}$ 桶排的代价

  桶排序利用函数的映射关系，减少了几乎所有的比较工作。实际上，桶排序的f(k)值的计算，其作用就相当于快排中划分，已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可

  >>> 对 $n$ 个关键字进行桶排序的时间复杂度分为两个部分：
(1) 循环计算每个关键字的桶映射函数，这个时间复杂度是 $O(n)$
(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序，其时间复杂度为 $\sum O(ni\log ni)$。其中 $ni$ 为第 $i$ 个桶的数据量

  很显然，第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到 $O(n\log n)$ 了)

  >>> 因此，我们需要尽量做到下面两点：
(1) 映射函数 $f(k)$ 能够将 $n$ 个数据平均的分配到 $m$ 个桶中，这样每个桶就有 $[n/m]$ 个数据量。
(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据，这样就完全避开了桶内数据的“比较”排序操作。 当然，做到这一点很不容易，数据量巨大的情况下，$f(k)$ 函数会使得桶集合的数量巨大，空间浪费严重。

(时间还是空间？这是一个问题)

  对于 $n$ 个待排数据，$m$ 个桶，平均每个桶 $[n/m]$ 个数据的桶排序平均时间复杂度为：
$O(n)+O(m\ast (n/m)\ast \log (n/m))=O(n+n\ast (\log n-\log m))=O(n+n\log n-n\log m)$

  当 $n=m$ 时，即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到 $O(n)$。
总结：桶排序的平均时间复杂度为线性的 $O(n+c)$，其中 $c=n(\log n-\log m)$ 。如果相对于同样的 $n$，桶数量 $m$ 越大，其效率越高，最好的时间复杂度达到 $O(n)$。当然桶排序的空间复杂度为 $O(n+m)$，如果输入数据非常庞大，而桶的数量也非常多，则空间代价无疑是昂贵的。此外，桶排序是稳定的。

3. 特性

• 稳定的
• 空间复杂度：$O(n+k)$
• 时间复杂度：$O(n+k)$
• 自适应：不适应
  
  

4.图解:

5.函数原型（似乎也不太标准）

(1) 低配版

// Bucket Sort 01
void Bucketsort01(int *a, int n) {
	// 桶的数量因题而异
	int bucket[100005], maxn = INT_MIN, minn = INT_MAX; 
	for (int i = 1; i <= n; i++) {
		bucket[a[i]]++; // 这里每个桶的范围都是1，所以直接对应桶加一
		minn = min(a[i], minn); // 找最大最小值边界
		maxn = max(a[i], maxn);
	} 
	for (int i = minn; i <= maxn; i++) {
		while (bucket[i] > 0) { // 桶不为空
			printf("%d ", i); // 输出该桶代表的数
			bucket[i]--; // 桶内元素减少一
		}
	}
	return ;
}

(2) 正常版

// Bucket Sort
void Sort(queue<int> &q, int n) { // 将队列排至有序
	int ans[n + 5]; // 定义辅助数组
	for (int i = 1; i <= n; i++) { // 将队列元素放入数组
		ans[i] = q.front();
		q.pop();
	} 
	sort(ans + 1, ans + n + 1); // 将数组排至有序
	for (int i = 1; i <= n; i++) { // 将有序的数组重新放回队列
		q.push(ans[i]);
	} 
	return ;
}
void Bucketsort(int *a, int n) {
	int maxn = INT_MIN, minn = INT_MAX;
	for (int i = 1; i <= n; i++) { // 计算最大值与最小值
		maxn = max(a[i], maxn);
		minn = min(a[i], minn);
	}
	int bucketsum = (maxn - minn) / n + 1; // 计算桶的数量
	queue<int> q[bucketsum];
	for (int i = 1; i <= n; i++) { // 将每个元素放入桶
		int num = (a[i] - minn) / n;
		q[num].push(a[i]);
	}
	int cnt = 0;
	for (int i = 0; i < bucketsum; i++) {
		Sort(q[i], q[i].size()); // 对每个桶进行排序
		while (!q[i].empty()) { // 将桶中的元素赋值到原序列
			a[++cnt] = q[i].front();
			q[i].pop();
		}
	}
	return ;
}

（（鸣谢乐府提供的 Idea

真 · 一个奇怪的小知识~

  桶排序的稳定性取决于桶内排序使用的算法。当数据跨度过大时，这个空间消耗就会很大；如果数值的范围特别大，那么对空间消耗的代价肯定也是不切实际的，所以这个算法还有一定的局限性。

---

$\text{Question and Answer}$

$\text{Q1:}$ 如何评价一个排序算法?

$\text{A:}$ 对于一个排序算法的评价，一般有以下几个标准：

1. 时间复杂度：最好、最坏、平均
     通常对于基于比较的排序算法，最好就是顺序排列时，最坏就是逆序排列时，平均就是随机排列时。因为不同的算法在不同的情形下表现可能大不相同，因为我们需要根据实际情况，选择最佳算法

>>> 时间复杂度的系数，常数，低阶

  当用 $Big-O$ 分析的时候，通常忽略这些细节，但是 $Big-O$ 针对的是数据规模很大的情况下的增长趋势。而排序算法，很多情况下是限定规模的， 比如 10， 1000， 100万，因此这些被忽略的项需要加上才能比较不同算法的优劣。

2. 比较次数和交换（或移动）的次数
   
     尤其是对于基于比较的排序算法，核心就两步，比较–交换， 统计次数尤为重要。
   
   

3. 算法的内存消耗
   
     即空间复杂度，如果是原地排序（sorted in place），空间复杂度就是 $O(1)$
   
   

4. 算法的稳定性
   当排序后需要保持相同元素相对位置不发生改变时，使用稳定排序。没有要求时可自由使用

$\text{Q2:}$ 按时间复杂度、稳定性把排序算法分类怎么分?

$\text{A:}$

关于时间复杂度

• 平方阶 $O(n^2)$ ：直接插入，直接选择，冒泡排序
• 线性对数阶 $O(n\log n)$ ： 快速排序，堆排序，归并排序
• $O(n^{\S })$ ( § 是介于 0 和 1 之间的常数 )： 希尔排序
• 线性阶 $O(n)$ 排序： 计数排序，基数排序，桶排序

关于稳定性

• 稳定排序：冒泡排序，插入排序，归并排序，计数排序，基数排序，桶排序
• 不稳定排序：选择排序，快速排序，希尔排序，堆排序

$\text{Q3:}$ 时间复杂度怎么增长，它们有什么区别?

$\text{A:}$

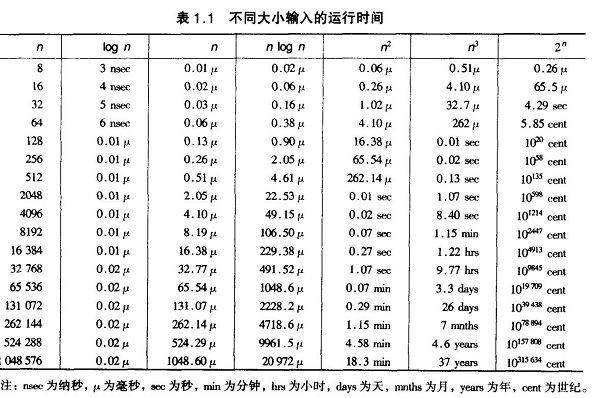
时间复杂度函数O(n)的增长情况：

图1

图2

$\text{Q4:}$ 这些算法有什么差异?

$\text{A:}$

• 直接插入排序：是对冒泡排序的改进，比冒泡排序快，但是只适用于数据量较小 (1000以下) 的排序
• 希尔排序：比较简单，适用于小数据量（5000以下）的排序，比直接插入排序、冒泡排序快，因此，希尔排序适用于小数据量的、排序速度要求不高的排序
• 直接选择排序：经常使用它内部的循环方式来找最大值和最小值。和冒泡排序算法一样，适用于数据量较小的场合，而且是排序算法发展的初级阶段，在实际应用中采用的几率较小
• 堆排序：用到了二叉堆数据结构，是继续掌握树结构的起手式，比较适用于数据量达到百万及其以上的排序，在这种情况下，使用递归设计的快速排序和归并排序可能会发生堆栈溢出的现象（蒟蒻摸鱼人曾遭过）
• 冒泡排序：效率太低，通过冒泡可以掌握swap。是最慢的排序算法，是排序算法发展的初级阶段，实际应用中采用该算法的几率比较小
• 快速排序：快排重视子问题拆分，是速度最快的递归排序算法，但是在数据基本有序的情况下不是一个好的选择，快速排序反而变得比较慢
• 归并排序：可以求逆序对数，比堆排序要快，但是需要的存储空间增加一倍，归并重视子问题的解的合并
• 计数排序：可以说是最快的，但计数排序的适用范围是：序列的关键字比较集中，已知边界，且边界较小
• 基数排序：适用于规模数据规模很大的场合，但是只适用于整数的排序，如果对浮点数进行基数排序，则必须明确浮点数的存储格式，然后通过某种方式将其映射到整数上，最后再映射回去，过程复杂
• 桶排序：用它解决问题必须注意序列的值是否均匀地分布在桶中。如果不均匀，极端情况下，全部元素在一个桶内，还是会退化

$\text{Q5:}$ 想看实际对比

$\text{A:}$ 好嘞

测试题目：#2625. 常用排序法

名称	状态	分数	总用时	内存
直接插入排序	TLE	95	1373ms	688K
希尔排序	AC	100	306ms	680K
直接选择排序	TLE	95	1663ms	864K
堆排序	AC	100	227ms	968K
冒泡排序	TLE	95	2848ms	732K
鸡尾酒排序	TLE	95	2548ms	636K
快速排序(2路)	AC	100	217ms	880K
快速排序(挖坑法)	AC	100	193ms	876K
快速排序(前后指针法)	AC	100	213ms	760K
快速排序(3路)	AC	100	217ms	784K
归并排序	AC	100	215ms	1264K
计数排序	AC	100	205ms	884K
基数排序	AC	100	211ms	1220K
桶排（低配版）	AC	100	221ms	872K
桶排（正常版）	AC	100	213ms	1664K

---

小测验

1.测验：在任何大小为 N 的输入数组上，这些算法中的哪一个以 O(N log N) 的速度运行？

a. 快速排序（确定性）
b. 插入排序
c. 合并排序
d. 冒泡排序

2.测验（不定项）：在对 N 个整数进行排序时，哪些算法的最坏情况时间复杂度为 $\Theta (N^2)$？

a. 选择排序
b. 插入排序
c. 合并排序
d. 基数排序
e. 冒泡排序

注：$\Theta$ 是一个紧密的时间复杂度分析，其中最佳情况 $\Omega$ 和最坏情况的 $big-O$ 分析互相匹配

Answer :

1. c
2. a, b, e

---

(笑死，写这玩意儿电脑差点芭比Q)