【链表实现】一元多项式相加相乘【详解相加相乘】
目录
一、一元多项式的表示
1、概念
2、用什么数据结构实现?
二、一元多项式的实现
1、基本结构概况
2、创建一元多项式
3、节点的尾插
4、一元多项式相加
5、一元多项式相乘
6、多项式的打印
7、 Poly的析构函数
8、完整代码
Poly.h:
Poly.cpp
test.cpp
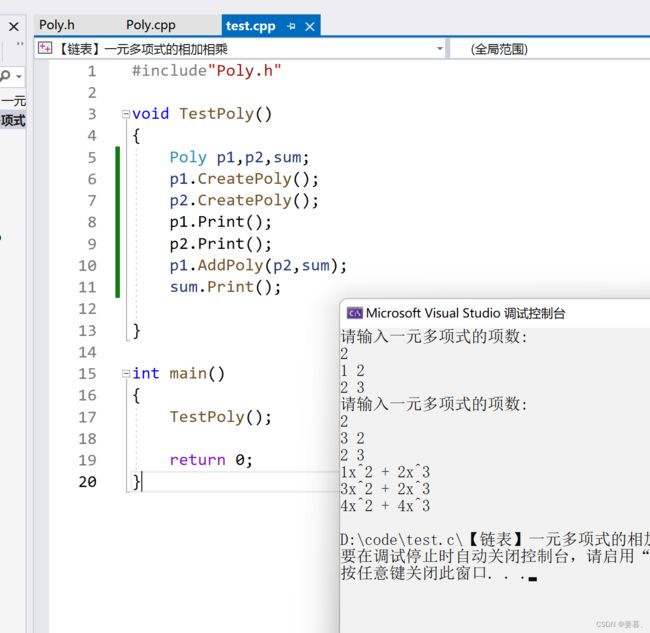
9、运行测试
三、艰难的调试过程(可不看,我自己看的)
一、一元多项式的表示
1、概念
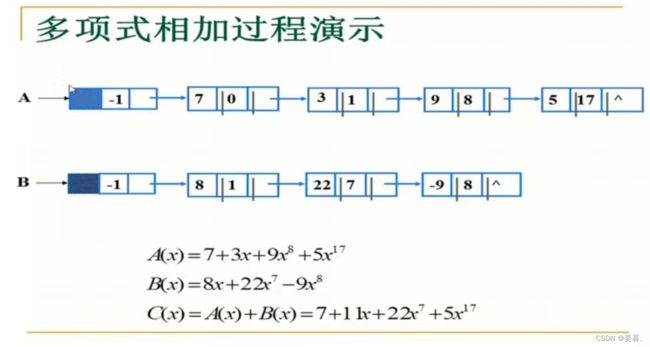
形如:Pn(x) = P0 + P1x + p2X^2 + ...... + Pnx^n就叫n阶多项式
n阶多项式Pn(x)有 n+1 项
- 系数:P0,P1,P2,......Pn
- 指数:0,1,2,......,n,按升幂排列
2、用什么数据结构实现?
可见用顺序表存储会很浪费空间,故用链表来存储
其优点:
- 多项式的项数可以动态的增长,不存在存储溢出问题
- 插入、删除方便,不移动数据
二、一元多项式的实现
分三个文件实现
Poly.h Poly.cpp test.cpp
1、基本结构概况
//链表的多项式节点
struct Polynode
{
int _coef;//系数
int _exp;//指数
struct Polynode* _next;
Polynode(int coef = 0,int exp = 0)
:_next(nullptr)
,_coef(coef)
,_exp(exp)
{}
~Polynode()
{
_next = nullptr;
}
};
//一元多项式
class Poly
{
public:
void CreatePoly();//创建
void Print();//打印
void Push_back(Polynode* node);//尾插
void AddPoly(Poly& p2, Poly& sum);//相加
void MultiPoly(Poly& p2, Poly& sum);//相乘
~Poly();//析构
private:
Polynode* _head = new Polynode;//直接开辟个头结点
};2、创建一元多项式
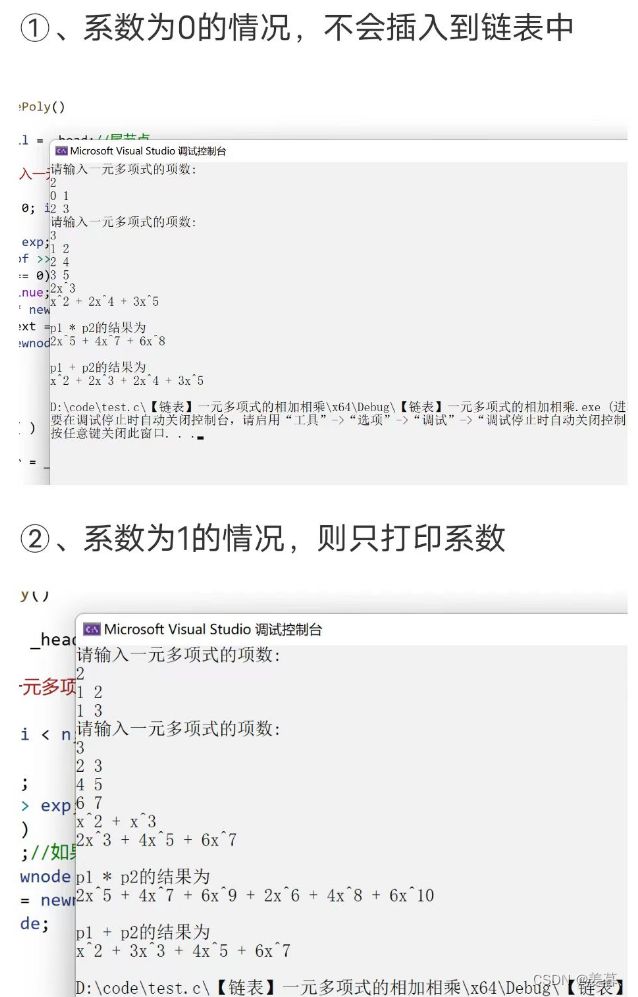
不断创建新节点尾插即可,但要注意若输入的系数为0,没必要插入此节点,直接continue
//创建一元多项式
void Poly::CreatePoly()
{
Polynode* tail = _head;//尾节点
int n = 0;
cout << "请输入一元多项式的项数:" << endl;
cin >> n;
for (int i = 0; i < n; ++i)
{
int cof, exp;
cin >> cof >> exp;
if (cof == 0)
continue;//如果系数==0,则不插入此节点
Polynode* newnode = new Polynode(cof, exp);//创建新节点
tail->_next = newnode;//链接
tail = newnode;
}
}3、节点的尾插
//节点的尾插
void Poly::Push_back(Polynode* node)
{
Polynode* tail = _head->_next;
if (tail == nullptr)
{//若链表为空,直接插入
_head->_next = node;
}
else
{
while (tail->_next)
{ //找到尾节点
tail = tail->_next;
}
tail->_next = node;
}
}4、一元多项式相加
//一元多项式的相加(利用一元多项式指数是升序的特点)
//p1 + p2
void Poly::AddPoly(Poly& p2,Poly& sum)
{
Polynode* cur1 = _head->_next, * cur2 = (p2._head)->_next;//cur用来遍历
Polynode* head = sum._head;
while (cur1 && cur2)
{ //都不为空才会进入循环
//1、p1的指数p2的指数
//3、p2的指数=p2的指数:
// ①、系数相加为0,删除cur1和cur2的对应节点
// ②、不为0,加和到cur1上,尾插到sum后面
if (cur1->_exp < cur2->_exp)
{
head->_next = cur1;
head = cur1;
cur1 = cur1->_next;
}
else if (cur1->_exp > cur2->_exp)
{
head->_next = cur2;
head = cur2;
cur2 = cur2->_next;
}
else
{
//①、系数相加为0
if (cur1->_coef + cur2->_coef == 0)
{
Polynode* next1 = cur1->_next;
Polynode* next2 = cur2->_next;
delete cur1;
delete cur2;
cur1 = next1;
cur2 = next2;
}
else
{//②、系数相加不为0
cur1->_coef = cur1->_coef + cur2->_coef;
head->_next = cur1;
head = cur1;
cur1 = cur1->_next;
Polynode* next = cur2->_next;
delete cur2;
cur2 = next;
}
}
}
if (cur1)
{//若cur1不为空
head->_next = cur1;
}
if (cur2)
{//若cur2不为空
head->_next = cur2;
}
}
5、一元多项式相乘
相乘的逻辑就是双层循环,对于链表怎么双重循环,思路就是对于第一个多项式的第一项乘以第二个多项式的每一项,然后第一个多项式的第二项乘以第二个多项式的每一项....直到乘到结束
//一元多项式的相乘
//p1 * p2
void Poly::MultiPoly(Poly& p2, Poly& sum)
{
Polynode* cur1 = _head->_next, * cur2 = (p2._head)->_next;//cur用来遍历
int cofs = 0, exps = 0;
while (cur1)
{
cur2 = (p2._head)->_next;//再次回到头结点的下一位置
while (cur2)
{
cofs = cur1->_coef * cur2->_coef;//系数相乘
exps = cur1->_exp + cur2->_exp;//指数相加
Polynode* newnode = new Polynode(cofs, exps);
sum.Push_back(newnode);
cur2 = cur2->_next;
}
cur1 = cur1->_next;
}
}6、多项式的打印
存在特殊情况考虑:
①、若系数为1,指数不为0,只打印x^指数
②、若系数为1,指数为0,只打印1
③、若系数不为0,指数为0,只打印系数
④、若系数为负数,要给系数加上()
//打印一元多项式
void Poly::Print( )
{
Polynode* cur = _head->_next;
while (cur)
{
//当指数!=0时,才会打印出x
if (cur->_exp != 0)
{
//当系数!=1时,才会打印出系数
if (cur->_coef != 1)
{
if (cur->_coef < 0)
{
cout << "(" << cur->_coef;
cout << ")x^" << cur->_exp;
}
else
{
cout << cur->_coef;
cout << "x^" << cur->_exp;
}
}
else
{//当系数==1时,指数不为0时
cout << "x^" << cur->_exp;
}
}
else
{ //若指数为0,只打印系数
if (cur->_coef != 1)
{//系数不为1,则只打印系数
if (cur->_coef < 0)
{
cout << "(" << cur->_coef;
cout << ")";
}
else
{
cout << cur->_coef;
}
}
else
{
cout << "1";//若系数为1,指数为0,则打印1
}
}
cur = cur->_next;
if (cur != NULL)
{//最后一项之前才会打印加号
cout << " + ";//正数打印+
}
}
cout << endl;
}
7、 Poly的析构函数
//析构函数
Poly::~Poly()
{
delete _head;
_head = nullptr;
}8、完整代码
Poly.h:
#pragma once
#include
using namespace std;
//链表的多项式节点
struct Polynode
{
int _coef;//系数
int _exp;//指数
struct Polynode* _next;
Polynode(int coef = 0,int exp = 0)
:_next(nullptr)
,_coef(coef)
,_exp(exp)
{}
~Polynode()
{
_next = nullptr;
}
};
//一元多项式
class Poly
{
public:
void CreatePoly();//创建
void Print();//打印
void Push_back(Polynode* node);//尾插
void AddPoly(Poly& p2, Poly& sum);//相加
void MultiPoly(Poly& p2, Poly& sum);//相乘
~Poly();//析构
private:
Polynode* _head = new Polynode;//直接开辟个头结点
};
Poly.cpp
#include"Poly.h"
//创建一元多项式
void Poly::CreatePoly()
{
Polynode* tail = _head;//尾节点
int n = 0;
cout << "请输入一元多项式的项数:" << endl;
cin >> n;
for (int i = 0; i < n; ++i)
{
int cof, exp;
cin >> cof >> exp;
if (cof == 0)
continue;//如果系数==0,则不插入此节点
Polynode* newnode = new Polynode(cof, exp);//创建新节点
tail->_next = newnode;//链接
tail = newnode;
}
}
//打印一元多项式
void Poly::Print( )
{
Polynode* cur = _head->_next;
while (cur)
{
//当指数!=0时,才会打印出x
if (cur->_exp != 0)
{
//当系数!=1时,才会打印出系数
if (cur->_coef != 1)
{
if (cur->_coef < 0)
{
cout << "(" << cur->_coef;
cout << ")x^" << cur->_exp;
}
else
{
cout << cur->_coef;
cout << "x^" << cur->_exp;
}
}
else
{//当系数==1时,指数不为0时
cout << "x^" << cur->_exp;
}
}
else
{ //若指数为0,只打印系数
if (cur->_coef != 1)
{//系数不为1,则只打印系数
if (cur->_coef < 0)
{
cout << "(" << cur->_coef;
cout << ")";
}
else
{
cout << cur->_coef;
}
}
else
{
cout << "1";//若系数为1,指数为0,则打印1
}
}
cur = cur->_next;
if (cur != NULL)
{//最后一项之前才会打印加号
cout << " + ";//正数打印+
}
}
cout << endl;
}
//节点的尾插
void Poly::Push_back(Polynode* node)
{
Polynode* tail = _head->_next;
if (tail == nullptr)
{//若链表为空,直接插入
_head->_next = node;
}
else
{
while (tail->_next)
{ //找到尾节点
tail = tail->_next;
}
tail->_next = node;
}
}
//一元多项式的相加(利用一元多项式指数是升序的特点)
//p1 + p2
void Poly::AddPoly(Poly& p2,Poly& sum)
{
Polynode* cur1 = _head->_next, * cur2 = (p2._head)->_next;//cur用来遍历
Polynode* head = sum._head;
while (cur1 && cur2)
{ //都不为空才会进入循环
//1、p1的指数p2的指数
//3、p2的指数=p2的指数:
// ①、系数相加为0,删除cur1和cur2的对应节点
// ②、不为0,加和到cur1上,尾插到sum后面
if (cur1->_exp < cur2->_exp)
{
head->_next = cur1;
head = cur1;
cur1 = cur1->_next;
}
else if (cur1->_exp > cur2->_exp)
{
head->_next = cur2;
head = cur2;
cur2 = cur2->_next;
}
else
{
//①、系数相加为0
if (cur1->_coef + cur2->_coef == 0)
{
Polynode* next1 = cur1->_next;
Polynode* next2 = cur2->_next;
delete cur1;
delete cur2;
cur1 = next1;
cur2 = next2;
}
else
{//②、系数相加不为0
cur1->_coef = cur1->_coef + cur2->_coef;
head->_next = cur1;
head = cur1;
cur1 = cur1->_next;
Polynode* next = cur2->_next;
delete cur2;
cur2 = next;
}
}
}
if (cur1)
{//若cur1不为空
head->_next = cur1;
}
if (cur2)
{//若cur2不为空
head->_next = cur2;
}
}
//一元多项式的相乘
//p1 * p2
void Poly::MultiPoly(Poly& p2, Poly& sum)
{
Polynode* cur1 = _head->_next, * cur2 = (p2._head)->_next;//cur用来遍历
int cofs = 0, exps = 0;
while (cur1)
{
cur2 = (p2._head)->_next;//再次回到头结点的下一位置
while (cur2)
{
cofs = cur1->_coef * cur2->_coef;//系数相乘
exps = cur1->_exp + cur2->_exp;//指数相加
Polynode* newnode = new Polynode(cofs, exps);
sum.Push_back(newnode);
cur2 = cur2->_next;
}
cur1 = cur1->_next;
}
}
//析构函数
Poly::~Poly()
{
delete _head;
_head = nullptr;
}
test.cpp
#include"Poly.h"
void TestPoly()
{
Poly p1,p2,sum1,sum2;
p1.CreatePoly();
p2.CreatePoly();
p1.Print();
p2.Print();
cout << endl;
cout << "p1 * p2的结果为" << endl;
p1.MultiPoly(p2, sum2);
sum2.Print();
cout << endl;
cout << "p1 + p2的结果为" << endl;
p1.AddPoly(p2,sum1);
sum1.Print();
}
int main()
{
TestPoly();
return 0;
}9、运行测试
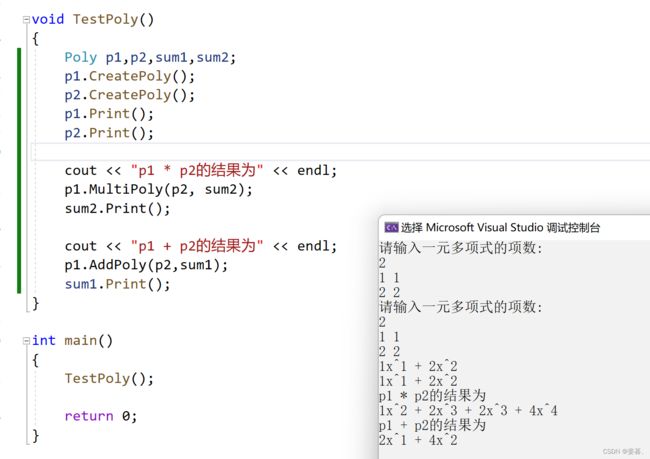
最后,代码还存在一个问题,相同的指数的x项相加后,相乘后没有合并,这里我就不写了
三、艰难的调试过程(可不看,我自己看的)
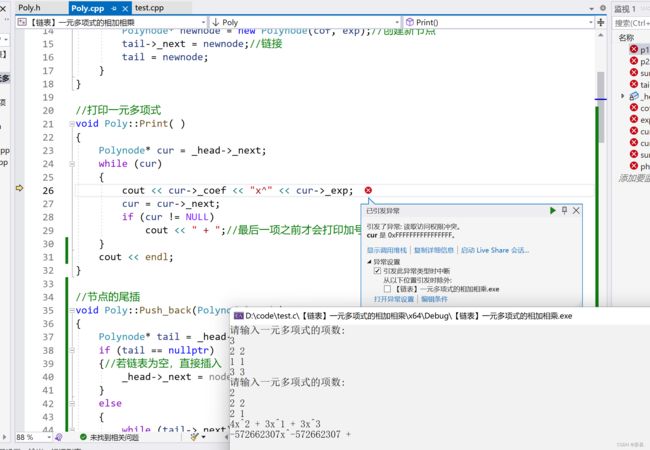
在我写完多项式相加后,创建多项式后程序直接给我卡死在这,但是之前测试打印什么的都没问题,那问题可能出现在了AddPoly
经调试发现是AddPoly的插入有问题,尾插的时候什么时候该删除,什么是否不该删除节点我没搞清楚
AddPoly代码逻辑修改完后又出现了问题:但是没有Addpoly的调用,代码打印p2还是没问题,说明加了AddPoly后p2的打印有问题,可能是删除方面出现了问题
经过不断的调试,我发现问题在于调用的顺序,因为调用AddPoly后p2或者p1的部分数据会被删除的,故你想打印p1和p2,必须在调用AddPoly之前再调用,不然就非法访问了,这就是一个很小的问题
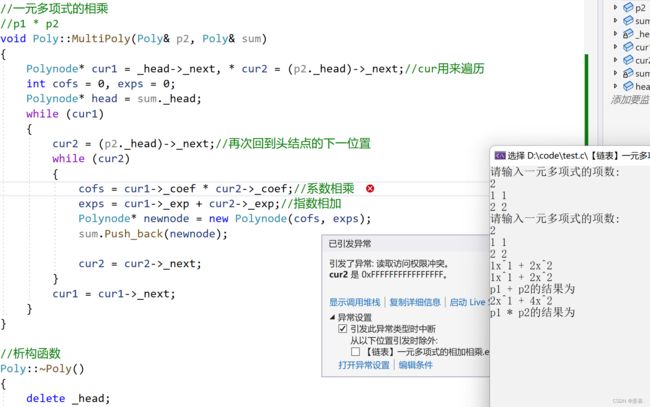
在实现相乘的时候又出错了
但是如果把AddPoly注释掉就可以正常运行MultiPoly了,还是一样的问题,AddPoly应该放在最后调用,因为他破坏了p1或p2,或者你相乘换个数据,不用p1和p2也行
调用时相加放在后面就可以解决问题了