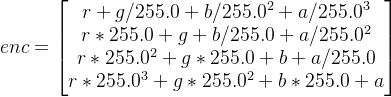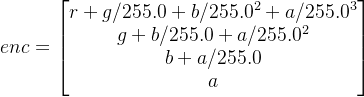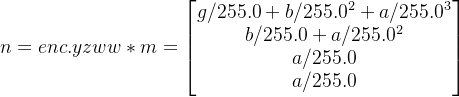Cesium 源码解析 float 与 rgba相互转化

        cesium中将float转换为rgba主要是为了解决显卡不支持float类型纹理的问题，例如将像素着色器中的深度提取出来，由于在opengl的规范当中将pixel shader中的数据提取出来的方法是保存成像素值，而低端的显卡硬件都支持将像素保存成rgba格式的[0~1]范围的值，这就需要将float转换成rgba的方式进行渲染，而后在将这个渲染出的结果中还原原来的float数据。

        cesium中glsl相关的代码是：

/**
 * Unpacks a vec4 depth value to a float in [0, 1) range.
 *
 * @name czm_unpackDepth
 * @glslFunction
 *
 * @param {vec4} packedDepth The packed depth.
 *
 * @returns {float} The floating-point depth in [0, 1) range.
 */
 float czm_unpackDepth(vec4 packedDepth)
 {
    // See Aras Pranckevičius' post Encoding Floats to RGBA
    // http://aras-p.info/blog/2009/07/30/encoding-floats-to-rgba-the-final/
    return dot(packedDepth, vec4(1.0, 1.0 / 255.0, 1.0 / 65025.0, 1.0 / 16581375.0));
 }

/**
 * Packs a depth value into a vec3 that can be represented by unsigned bytes.
 *
 * @name czm_packDepth
 * @glslFunction
 *
 * @param {float} depth The floating-point depth.
 * @returns {vec3} The packed depth.
 */
vec4 czm_packDepth(float depth)
{
    // See Aras Pranckevičius' post Encoding Floats to RGBA
    // http://aras-p.info/blog/2009/07/30/encoding-floats-to-rgba-the-final/
    vec4 enc = vec4(1.0, 255.0, 65025.0, 16581375.0) * depth;
    enc = fract(enc);
    enc -= enc.yzww * vec4(1.0 / 255.0, 1.0 / 255.0, 1.0 / 255.0, 0.0);
    return enc;
}

整个计算过程如下：

1 将float转换为rbga的过程vec4 czm_packDepth(float depth)如下：

1.1 假设depth为深度值，这个深度值是介于(0~1)开区间之间的，对于不在这个范围内的值可以将这个值除以远裁切面，既然在(0~1)之间，我们可以假设depth为下面的结果，至于为什么可以这样拆解，主要是depth的范围(0~1),而rgba中每个分量也在[0~1]之间，同时因为数据压缩了，必定会出现精度损失，但是在这个可以认为这个精度可以接受，所以g/255.0、b/255.0/255.0会很小,可以拆解成下面的结果。

        

1.2 对于代码的第一步，对应的计算过程enc,假设一个中间量key,

       

       

        

1.3 对于代码的第二步，将enc向量中的每个成员取小数, 因为

         

1.4  假设一个中间变量m为

        

        

       

所以结果就是原来depth假设的各个分量

1.5 如何将result还原为原来的depth,

        

                   

总结：

        对于float转rgba的原理，可以参考位权的方式，例如对于1234这个十进制数，按照位权展开是

                1234 = 1*10^3 + 2*10^2 + 3*10^1 + 4

如果将1234这个整数存储在rgba中，假如每个分量存储空间是4位，那么r=1，g=2, b=3, a=4;

        而对于真实情况向rgba，每个分量的存储空间是8位[0-255],将将原来的数据按照255的位权展开（即255进制），就可以提取出每个位权对应的数据。

              1234 = 4*255 + 214

所以        r=0，g=0, b=4, c=255

        对于存储shader中的depth方法而言，可以存储经过透视除法之后的深度信息，因为此时的depth范围为[0~1],是一个小数，如何将小数转换成byte类型的rgba数据呢，还是使用位权的方式，计算机相关的书籍都会将如何存储将10进制小数转换为二进制小数的方式，或者将二进制小数转换为10进制小数。

        (11.75)d转化为(1011.11)b，同理将[0~1]之间的的小数转换成rgba就可以按照这种方法，整数部分除以255，小数部分乘以255*255*255取r,g,b,a.的方式。