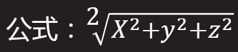三维数学（一）

视频教程：https://www.bilibili.com/video/BV12s411g7gU?p=155

目录

向量

向量的运算（一）

三角函数

向量运算（二）

向量常用属性及方法

---

向量

一个数字列表，表示各个维度上的有向位移；同时也是一个有大小有方向的物理量，大小及向量的模长，而方向即空间中向量的指向，可以表示物体的位置和方向

向量的形式

 

向量的大小(模)

向量各分量平方和的平方根 

  

API : 

Vector3.magnitude：模长

Vector3..sqrMagnitude：模长的平方

向量的方向 

获取向量方向也称“标准化向量”，或“归一化向量”，即该向量的单位向量（大小为1的向量）。

几何意义︰将该向量拉长或者缩短，使模长等于1

  

API：

Vector3.normalized：获取该向量的单位向量

Vector3 vector2=vector1.normalized;//vector2为vector1的单位向量

Vector3.Normalize：将该向量自身设置为单位向量

vector1.Normalize();//将vector1自身设置为单位向量

private void Update()
{
    Demo01();
    Demo02();
}

//模长
private void Demo01()
{
    Vector3 pos = this.transform.position;

    float m01 = Mathf.Sqrt(Mathf.Pow(pos.x, 2) + Mathf.Pow(pos.y, 2) + Mathf.Pow(pos.z, 2));
    float m02 = pos.sqrMagnitude;
    float m03 = Vector3.Distance(Vector3.zero, pos);

    Debug.LogFormat("{0}--{1}--{2}", m01, m02, m03);
    
    Debug.DrawLine(Vector3.zero, pos);
}

//方向
private void Demo02()
{
    Vector3 pos = this.transform.position;
    Vector3 n01 = pos / pos.magnitude;
    Vector3 n02 = pos.normalized;

    Debug.DrawLine(Vector3.zero, n02, Color.red);
}

向量的运算（一）

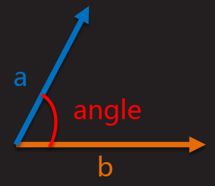
向量相减：等于各分量相加减，应用于计算两点间的距离和相对方向

几何意义：向量a与向量b相减，结果理解为以b的终点为始点，以a的终点为终点的向量。方向由b指向a

 

向量相加：等于各分量相加和，应用于物体移动 

几何意义：向量a与向量b相加，平移使b的始点与a的终点重合，结果为以a的始点为始点，以b的终点为终点的向量

向量与标量的乘除 

乘法：该向量的各分量与标量相乘；k[xy,z]= [xk,yk,zk]

除法：该向量的各分量与标量相除；[x,y,z]/k = [x/k,y/k,z/k]

几何意义：缩放向量长度  

ps：当要将某一将向量缩放至特定长度，可以先获取该向量的方向向量，再乘/除以比例系数

public Transform t1, t2, t3;

private void Update()
{
    Demo03();
}

//向量运算
private void Demo03()
{
    //t1相对于t2的位置
    //其大小为两点间距离
    Vector3 relativeDirection = t1.position - t2.position;

    //t3沿relativeDirection方向移动
    if (Input.GetKeyDown(KeyCode.A))
    //获取方向向量，避免两物体间距离对速度造成影响
    //t3.Translate(relativeDirection.normalized * 0.5f);
    t3.position+=relativeDirection.normalized;

    Debug.DrawLine(Vector3.zero, relativeDirection);
}

三角函数

角的度量方式

PI=180度 1弧度=180度/PI 1角度=PI/180度

角度-->弧度：弧度=角度数*PI/180 

API：弧度=角度数*Mathf.Deg2Rad

弧度-->角度：角度=弧度数*180/PI

API：角度=弧度数*Mathf.Rad2Deg

private void Demo01()
{
    //角度-->弧度：弧度=角度数*PI/180
    float d1 = 60;
    float r1 = d1 * Mathf.PI / 180;
    float r2 = d1 * Mathf.Deg2Rad;
    print("角度-->弧度：" + d1 + "-->" + r1 + "/" + r2);
}

private void Demo02()
{
    //弧度-->角度：角度=弧度数*180/PI
    float r1 = 3;
    float d1 = r1 * 180 / Mathf.PI;
    float d2 = r1 * Mathf.Rad2Deg;
    print("弧度-->角度：" + r1 + "-->" + d1 + "/" + d2);
}

三角函数 

建立了直角三角形中角与边长比值的关系

正弦：sin x = a / c

余弦：cos x = b / c

正切：tan x = a / b 

API（以弧度为单位）：

正弦：Mathf.Sin

余弦：Mathf.Cos

正切：Mathf.Tan

反三角函数

反正弦，反余弦，反正切等函数的总称；可用于根据两边长，计算角度

反正弦：arcsin a / c = x

反余弦：arccos b / c = x

反正切：arctan a / b = x;

API（以弧度为单位）：

反正弦：Mathf.Asin

反余弦：Mathf.Acos

反正切：Mathf.Atan

private void Demo03()
{
    //已知角度x，边长b，求边长a
    float x = 50, b = 20;
    float a = Mathf.Tan(x * Mathf.Deg2Rad);

    //已知边长a，边长b，求角度angle
    float angle = Mathf.Atan(a / b) * Mathf.Rad2Deg;

    print(angle);
}

private void Demo04()
{
    //将自身坐标系转换到世界坐标系中
    //Vector3 worldPos = transform.TransformPoint(0, 0, 10);

    //计算物体前方30度，10m远的坐标
    float x = Mathf.Sin(30 * Mathf.Deg2Rad) * 10;
    float z = Mathf.Cos(30 * Mathf.Deg2Rad) * 10;
    Vector3 worldPos = transform.TransformPoint(x, 0, z);
    print(worldPos);
}

Transform.TransformPoint(Vector3 position)：将position从本地空间变换到世界空间

向量运算（二）

点乘

又称“点积”或”内积” 

  

几何意义：两个向量的单位向量相乘后再乘以二者夹角的余弦值 

a-b=|a|·|b| cos

应用：计算两向量夹角；对于标准化的向量，点乘结果等于两向量夹角的余弦值 

API： 

Vector3.Dot：两个向量的点积，点积是一个浮点值，等于将两个向量的大小相乘，然后乘以向量之间角度的余弦值

public Transform t1, t2, t3;
//点乘
//计算两向量夹角的cos值
float dot = Vector3.Dot(t1.position.normalized,t2.position.normalized);
float angle= Mathf.Acos(dot)*Mathf.Rad2Deg;

ps：点乘能计算两向量夹角的cos值，但无法确定角的象限；想要确定角的象限应结合向量的叉乘

对于标准化过的向量，若两方向相同，点乘结果为1；反之，点乘结果为-1；互相垂直结果为0

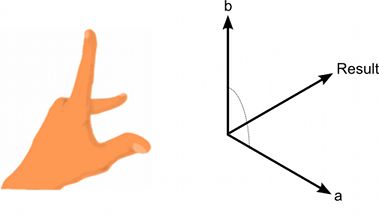
叉乘 

又称“叉积”或”外积”

几何意义：结果为两个向量所组成面的垂直向量，模长为两向量模长乘积再乘夹角的正弦值

应用：1.创建垂直于平面的向量；2.判断两条向量相对位置。

API：  

Vector3.Cross：两个向量的叉积，两个向量的叉积生成第三个向量， 该向量垂直于两个输入向量

//点乘
//计算两向量夹角的cos值
float dot = Vector3.Dot(t1.position.normalized,t2.position.normalized);
float angle= Mathf.Acos(dot)*Mathf.Rad2Deg;

//叉乘
Vector3 cross=Vector3.Cross(t1.position,t2.position);
if(cross.y<0)
{
    angle=360-angle;
}
Debug.DrawLine(Vector3.zero,cross);

ps：根据“左手规则”确定结果向量的方向

叉乘所得向量的模长与角度：0~90度

向量常用属性及方法

静态属性 

1.Vector3.up-->new Vector3(0,1,0)

2.Vector3.down-->new vector3(0,-1,0)

3.Vector3.left-->new Vector3(-1,0,0)

4.Vector3.right-->new Vector3(1,0,0)

5.Vector3.forward-->new Vector3(0,0,1)

6.Vector3.back-->new Vector3(0,0,-1)

静态方法

1.Vector3.Lerp&Vector3.LerpUnclamped

 Vector3.Lerp：

//将物体移动到(0,0,10)
//先快后慢 不能到达目标点（无限接近）
this.transform.position = Vector3.Lerp(this.transform.position, targetPos, 0.1f);

 Vector3.LerpUnclamped：

参数设置 

点击Curve属性编辑曲线 

public AnimationCurve curve;
private float x = 0;
//持续时间
public float duration;

x += Time.deltaTime / duration;
//自然运动 起始点固定 终点固定 比例根据曲线变化
this.transform.position = Vector3.LerpUnclamped(Vector3.zero, targetPos, curve.Evaluate(x));

2.Vector3.MoveTowards(Vector3 current, Vector3 target, float maxDistanceDelta)：计算current指定的点与target指定的点之间的位置，移动距离不超过maxDistanceDelta指定的距离

current	移动的起始位置
target	移动的目标位置
maxDistanceDelta	每次调用移动的距离

//将物体移动到(0,0,10)
//匀速移动，可到达目标点
this.transform.position = Vector3.MoveTowards(this.transform.position, targetPos, 1);

3.Vector3.SmoothDamp(Vector3 current, Vector3 target, ref Vector3 currentVelocity, float smoothTime, float maxSpeed= Mathf.Infinity, float deltaTime= Time.deltaTime)：随时间推移将一个向量逐渐改变为所需目标

current	当前位置
target	尝试达到的目标
currentVelocity	当前速度，此值由函数在每次调用时进行修改
smoothTime	达到目标所需的近似时间。值越小，达到目标的速度越快
maxSpeed	可以选择允许限制最大速度
deltaTime	自上次调用此函数以来的时间。默认情况下为 Time.deltaTime

4.Vector3.Angle(Vector3 from, Vector3 to)：返回两个向量之间的角度（以度为单位）

from	测量角度差的源向量
to	测量角度差的目标向量

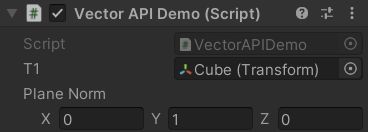
5.Vector3.ProjectOnPlane(Vector3 vector, Vector3 planeNormal)：将向量投影到由法线定义的平面上（法线与该平面正交）

planeNormal	从矢量到平面的方向
vector	平面上方的矢量的位置

public Transform t1;
public Vector3 planeNorm;
private Vector3 targetPos = new Vector3(0, 0, 10);

private void Update()
{
    Vector3 res = Vector3.ProjectOnPlane(t1.position, planeNorm);
    
    Debug.DrawLine(Vector3.zero, t1.position);
    Debug.DrawLine(Vector3.zero, res, Color.red);
}

参数设置 

 

运行 

 

6.Vector3.Reflect(Vector3 inDirection, Vector3 inNormal)：从法线定义的平面反射一个向量

inNormal向量定义一个平面（平面的法线是垂直于其表面的向量），inDirection向量被视为进入该平面的定向箭头，返回值是与inDirection大小相等、方向为其反射方向的向量