WKB近似
- WKB方法用于研究一种特定类型的微分方程的全局性质
- 很有用
- 这种特定的微分方程形如:
![]()
- 经过一些不是特别复杂的推导,我们可以得到他的WKB近似解。
- 该近似解的选择取决于函数
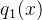 和参数
和参数 的性质
的性质 - 同时,我们默认函数的定义域为
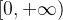
- 该近似解的选择取决于函数
- 当
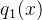 恒大于零,
恒大于零,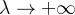 时:
时:
- 当
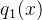 恒小于零,
恒小于零,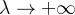 时:
时:
- 注:很快你会发现两个问题
- a 和 b 是怎么确定的
- 答:初始条件
- \lambda 趋于正无穷 并不意味着 只有 \lambda 很大才能使得该WKB 近似真实
- a 和 b 是怎么确定的
- 当
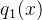 存在一个或者多个零点时,函数的WKB近似会变得非常的复杂
存在一个或者多个零点时,函数的WKB近似会变得非常的复杂
- 我们一会再看
WKB 近似案例 1
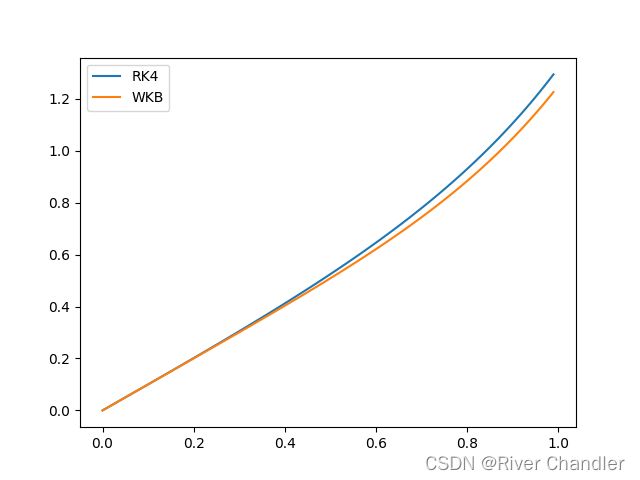
- 该案例选取自参考文献【1】P137 例5.1.1
import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import fsolve
class odessolver():
def __init__(self, f, Y_start=np.array([0, 1]), dY_start=np.array([0, 0]), \
X_start=0, X_end=1, h=0.01):
self.f = f
self.h = h
self.X = np.arange(X_start, X_end, self.h)
self.n = Y_start.size
self.Y = np.zeros((self.n, self.X.size))
#第一个参数表示元 第二个参数表示变量
self.Y[:, 0] = Y_start
self.Y[:, 1] = Y_start + self.h * dY_start
self.tol = 1e-6
def __str__(self):
return f"y'(x) = f(x) = ({self.f}) variables"
def RK4(self):
for i in range(1, self.X.size):
k1 = self.f(self.X[i-1] , self.Y[:, i-1])
k2 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k1)
k3 = self.f(self.X[i-1] +self.h/2 , self.Y[:, i-1]+1/2*self.h*k2)
k4 = self.f(self.X[i-1] +self.h , self.Y[:, i-1]+ self.h*k3)
self.Y[:, i] = self.Y[:, i-1] +self.h/6 * (k1 + 2*k2 + 2*k3 + k4)
return self.Y
def IRK4(self):
for i in range(1, self.X.size):
def f1(k1, k2):
f1_x = self.X[i-1] + self.h*(3-3**0.5)/6
f1_y = self.Y[:, i-1]+k1/4*self.h+(3-2*3**0.5)/12*k2*self.h
f1_res = self.f(f1_x, f1_y)
return np.array([f1_res[i] for i in range(self.n)])
def f2(k1, k2):
f2_x = self.X[i-1] + self.h*(3+3**0.5)/6
f2_y = self.Y[:, i-1]+k2/4*self.h+(3+2*3**0.5)/12*k1*self.h
f2_res = self.f(f2_x, f2_y)
return np.array([f2_res[i] for i in range(self.n)])
def func(k):
k1 = np.array([k[i] for i in range(self.n)])
k2 = np.array([k[i+self.n] for i in range(self.n)])
doc = []
for i in range(self.n):
doc.append((k1 - f1(k1, k2))[i])
for i in range(self.n):
doc.append((k2 - f2(k1, k2))[i])
return doc
sol = fsolve(func, np.zeros(self.n*2))
self.Y[:, i] = self.Y[:, i-1] + 1/2 * self.h * (sol[:self.n] + sol[self.n:])
return self.Y
A = 0
B = 1
Lambda = 1
Q = lambda x:(1+x**2)**2
Y0 = np.array([A, B])
def test_fun(x, Y):
return np.array([Y[1], Lambda**2 * Q(x) * Y[0]])
c = odessolver(test_fun, Y_start=Y0)
x = np.arange(0, 1, 0.01)
y3 = c.RK4()
x = np.arange(0, 1, 0.01)
plt.plot(x, y3[0, :], label="RK4")
##y4 = c.IRK4()
##x = np.arange(0, 1, 0.01)
##plt.plot(x, y4[0, :], label="IRK4")
WKB = lambda x:1/(Lambda*(1+x**2)**0.5)*(np.exp(x+x**3/3)-np.exp(-(x+x**3/3)))/2
plt.plot(x, WKB(x), label="WKB")
plt.legend()
plt.pause(0.01)
- 看上去十分得合理
参考文献
[1]数学物理中的渐近方法 李家春 周显初 科学出版社