leetcode721.账户合并(C/C++/Java/python)
PS:算法并非原创,仅作个人学习记录使用,侵删
题目描述
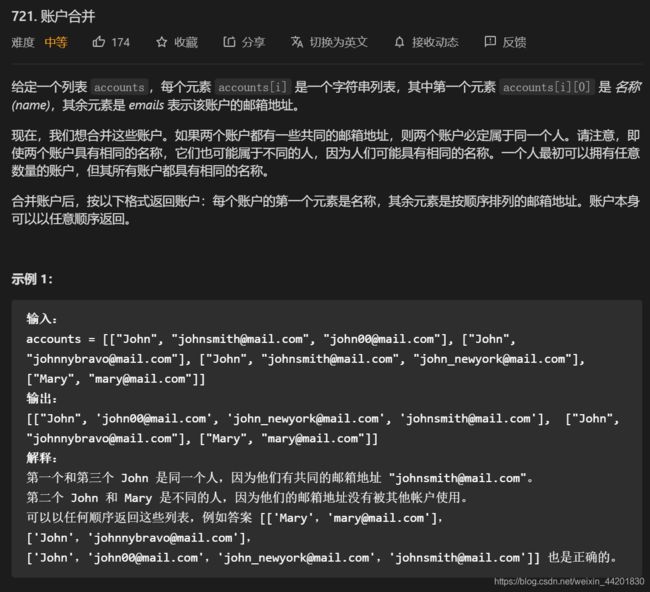
算法分析
个人的算法思路是:先合并相同账号,然后对每个账号的邮箱数组可以逐个进行字符串排序。
但是问题就在于:如何合并相同的账号?根据题目的意思,两个账号是否相同似乎只有一个评判标准:两个帐号是不是使用相同的邮箱地址。如果逐个比较的话,账号之间的配对相当多,似乎不是一个很好的方法。
但我也没办法想出更棒的想法了。
后来看了一些大佬的题解,没想到啊,竟然还能用并查集来解决。
并查集,yyds!
以下是官方题解:

代码实现
【C】
/*
C语言解法:哈希表+并查集
*/
#include C语言参考网址
【C++】
/*
C++解法:哈希表+并查集
*/
class UnionFind {
public:
vector<int> parent;
UnionFind(int n) {
parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
void unionSet(int index1, int index2) {
parent[find(index2)] = find(index1);
}
int find(int index) {
if (parent[index] != index) {
parent[index] = find(parent[index]);
}
return parent[index];
}
};
class Solution {
public:
vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {
map<string, int> emailToIndex;
map<string, string> emailToName;
int emailsCount = 0;
for (auto& account : accounts) {
string& name = account[0];
int size = account.size();
for (int i = 1; i < size; i++) {
string& email = account[i];
if (!emailToIndex.count(email)) {
emailToIndex[email] = emailsCount++;
emailToName[email] = name;
}
}
}
UnionFind uf(emailsCount);
for (auto& account : accounts) {
string& firstEmail = account[1];
int firstIndex = emailToIndex[firstEmail];
int size = account.size();
for (int i = 2; i < size; i++) {
string& nextEmail = account[i];
int nextIndex = emailToIndex[nextEmail];
uf.unionSet(firstIndex, nextIndex);
}
}
map<int, vector<string>> indexToEmails;
for (auto& [email, _] : emailToIndex) {
int index = uf.find(emailToIndex[email]);
vector<string>& account = indexToEmails[index];
account.emplace_back(email);
indexToEmails[index] = account;
}
vector<vector<string>> merged;
for (auto& [_, emails] : indexToEmails) {
sort(emails.begin(), emails.end());
string& name = emailToName[emails[0]];
vector<string> account;
account.emplace_back(name);
for (auto& email : emails) {
account.emplace_back(email);
}
merged.emplace_back(account);
}
return merged;
}
};
C++参考网址
【Java】
/*
Java解法:哈希表+dfs
*/
class Solution {
public List<List<String>> accountsMerge(List<List<String>> accounts) {
// 每个账号作为顶点,邮件相同的账号表示顶点相连。问题转换为求存在多少个连通子图。
HashMap<String, List<Integer>> emalIndex = new HashMap();
int aLen = accounts.size();
int index = 0;
for(List<String> list: accounts){
String name = list.get(0);
for(int i=list.size()-1; i>0; i--){
List<Integer> idxs = emalIndex.getOrDefault(list.get(i), new ArrayList());
idxs.add(index);
emalIndex.put(list.get(i), idxs);
}
index++;
}
// 获取相连的顶点
List<HashSet<Integer>> edges = new ArrayList();
for(int i=0; i< aLen; i++){
List<String> account = accounts.get(i);
HashSet<Integer> iset = new HashSet();
for(int j=account.size()-1; j> 0; j--){
String email = account.get(j);
if(emalIndex.containsKey(email)){
List<Integer> idxs = emalIndex.get(email);
iset.addAll(idxs);
}
}
edges.add(iset);
}
// 深度遍历,获取连通的子图。
List<List<String>> ret = new ArrayList();
boolean[] flags = new boolean[aLen];
for(int i=0; i< aLen; i++){
if(!flags[i]){
HashSet emails = new HashSet();
dfs(accounts, emails, edges, flags, i);
List<String> tmp = new ArrayList();
tmp.addAll(emails);
Collections.sort(tmp);
String name = accounts.get(i).get(0);
tmp.add(0, name);
ret.add(tmp);
}
}
return ret;
}
void dfs(List<List<String>> accounts, HashSet<String> emails, List<HashSet<Integer>> edges , boolean[] flags, int start){
List<String> acc = accounts.get(start);
emails.addAll(acc.subList(1, acc.size()));
flags[start] = true;
HashSet<Integer> set = edges.get(start);
if(set == null || set.size() == 0){
return;
}
for(Integer idx: set){
if(!flags[idx]){
dfs(accounts, emails, edges, flags, idx);
}
}
}
}
Java参考网址
【python】
#
#python解法:哈希表+dfs
#
class Solution:
def build_graph(self,accounts):
"""
建图
"""
graph = collections.defaultdict(list)
for account in accounts:
master = account[1]
# 对剩余账户做一个去重
for email in list(set(account[2:])):
graph[master].append(email)
graph[email].append(master)
return graph
def dfs(self,email,graph,visited,emails):
"""
深搜遍历
"""
# 已经访问过的就剪枝
if email in visited:
return
visited.add(email)
emails.append(email)
# 对邻居节点继续深搜
for neighbor in graph[email]:
self.dfs(neighbor,graph,visited,emails)
def accountsMerge(self, accounts):
graph = self.build_graph(accounts)
res = []
visited = set()
for account in accounts:
emails = []
self.dfs(account[1],graph,visited,emails)
if emails:
res.append([account[0]] + sorted(emails))
return res
python参考网址