外部排序&&多路归并排序 && 败者树&&实现java代码
目录
内部排序和外部排序
为什么外部排序得用多路归并?
概要
BAT 经典算法笔试题 —— 磁盘多路归并排序 - 掘金
外部排序的具体过程
流程思路概述
流程具体过程
多路归并排序的具体实现
内排序---简单二路归并参考力扣
二路归并排序的思路
外排序--k路归并排序--相关知识补充
外排序需要时间优化
优化归并过程---引入胜者树,败者树
胜者树图
败者树图
败者树的具体实现,java代码
辅助数据结构Chunk与Record
败者树LoserTree,直接运行main即可
整个外部排序的模拟实现代码
内部排序和外部排序
内部排序:整个的排序过程都在内存中进行排序
外部排序:对大文件进行排序,无法将整个需要排序的文件复制到内存,所以会把文件存储到外村,等排序时再把数据一部分一部分地调入内存进行排序,整个排序继续多次内存和外存的交换。
- 我们的k路归并排序,既可以作为内部排序又可以外部排序,这完全取决于使用场景,反正都行
- 外部排序一般都采用归并排序!
为什么外部排序得用多路归并?
概要
BAT 经典算法笔试题 —— 磁盘多路归并排序 - 掘金
原文链接:https://blog.csdn.net/a574780196/article/details/122646309
假定现在有一包含大量整数的文本文件存放于磁盘中,其文件大小为10GB,而本机内存只有4GB。此时若我们要对该文件中的所有整数进行升序排序,肯定不能直接将文件中的所有数据一次性读入内存中,再使用快速、归并等排序算法对这么大规模的整数进行排序。
好像陷入了难题? 我们不妨换一个思路,为何不将10GB大文件拆分为10个1GB的小文件呢? 逐个对10个文件进行排序后,再将其写入磁盘中,此时就得到了10份已排序后的临时文件。
每一份文件都是一个升序序列,这时问题就转换为如何合并这10路升序序列为1路升序序列。正因为待合并的数据路数比较多,所以才有了多路归并这一说法。
简单来说就是:
链接:https://juejin.cn/post/6844903762621005837
多路归并排序在大数据领域也是常用的算法,常用于海量数据排序。当数据量特别大时,这些数据无法被单个机器内存容纳,它需要被切分位多个集合分别由不同的机器进行内存排序(map 过程),然后再进行多路归并算法将来自多个不同机器的数据进行排序(reduce 过程),这是流式多路归并排序
外部排序的具体过程
参考:[HIT-DB-Lab3] 数据库的多路归并算法及其实现_z.q.xiao的博客-CSDN博客
参考:外部排序External-Sorting
参考天勤
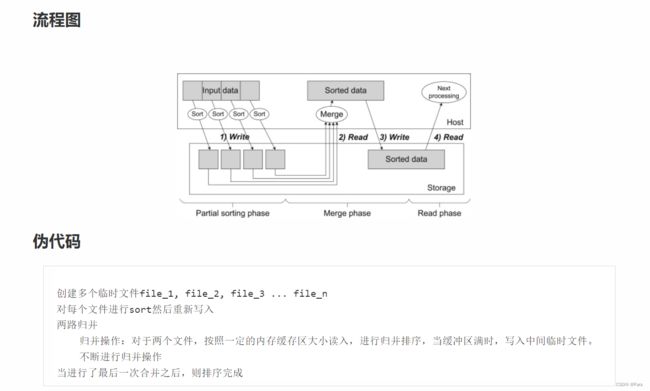
流程思路概述
流程具体过程
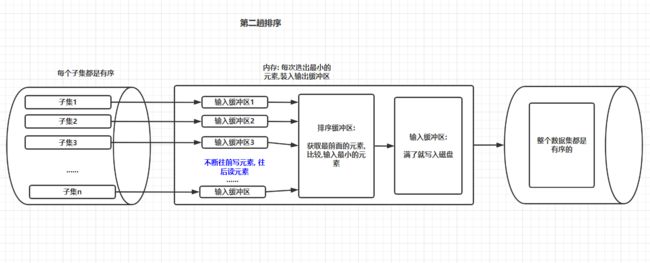
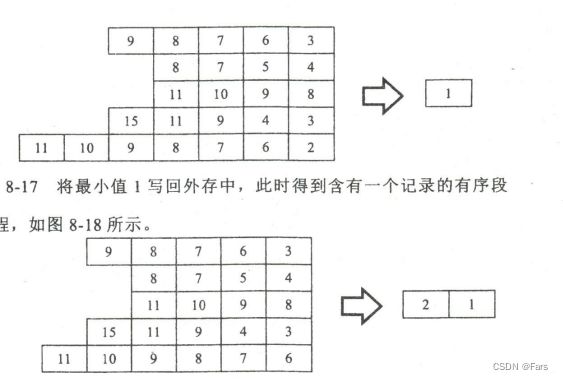
1.将外存大文件作为流输入,利用置换-选择排序算法---然后输出为多个小的已排序好的chunk(初始归并段)
采用置换-选择排序算法构造初始归并段的过程;根据缓冲区大小,由外存读入记录,当记录充满缓 冲区后,选择最小的(假设升序排序)写回外存,其空缺位置由下一个读入记录来取代,输出的记录成 为当前初始归并段的一部分
2.用败者树归并
- 通过败者树将刚才的多个chunk归并
- 利用败者树选择所有chunk中头部最小的元素,并把它放进外存,即ls[0]对应的bq
- 更换刚才被选出来的元素pop,换成它的chunk的下一个元素放在bq,调整败者树
- 如果某个chunk空了,则剔除该chunk,然后调整败者树
- 循环以上1~3直到全部chunk为空
这一步对应的是下图过程
多路归并排序的具体实现
内排序---简单二路归并参考力扣
void mergeSort(int[] nums, int l, int r) {
// 终止条件
if (l >= r) return;
// 递归划分
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 合并子数组
int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
for (int k = l; k <= r; k++)
tmp[k - l] = nums[k];
int i = 0, j = m - l + 1; // 两指针分别指向左/右子数组的首个元素
for (int k = l; k <= r; k++) { // 遍历合并左/右子数组
if (i == m - l + 1)
nums[k] = tmp[j++];
else if (j == r - l + 1 || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
}
}
}
// 调用
int[] nums = { 3, 4, 1, 5, 2, 1 };
mergeSort(nums, 0, len(nums) - 1);
作者:Krahets
链接:https://leetcode.cn/circle/article/zeM9YK/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。二路归并排序的思路
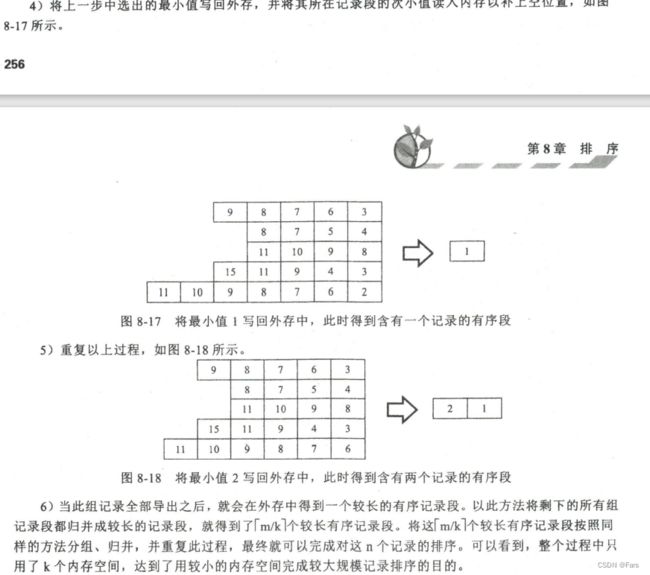
内排序-----简单2路归并图
内排序-----简单5路归并图
外排序--k路归并排序--相关知识补充
外排序需要时间优化
外部排序的总时间=内部排序所需的时间+外存信息读写的时间+内部归并所需的时间
显然,外存信息读写的时间远大于内部排序和内部归并的时间,因此应适当减少I/O次数
可以适当,增大归并路数,可减少归并趟数,进而减少总的磁盘I/O次数
优化归并过程---引入胜者树,败者树
不能用普通的内部归并->引入败者树
- 一般外部排序用的是败者树
- 胜者树的优点:一个选手的值改变了,可以很方便的修改当前胜者树
- 败者树可以说是胜者树的一个变种,是胜者树的一种优化,当一个选手的值改变了,比败者树可以很方便的修改当前胜者树
- 历史上:外部排序先用的最小堆,然后优化变种成了胜者树,再优化变种成了败者树
理解胜者树和败者树的关键:
胜者树和败者树都是拿赢家去比下一轮,但是不同的是,胜者树的中间结点记录的是胜者的标号;而败者树的中间结点记录的败者的标号。(败者树虽然记录的是败者标号,但是也依然会把胜者传给下一轮去比)
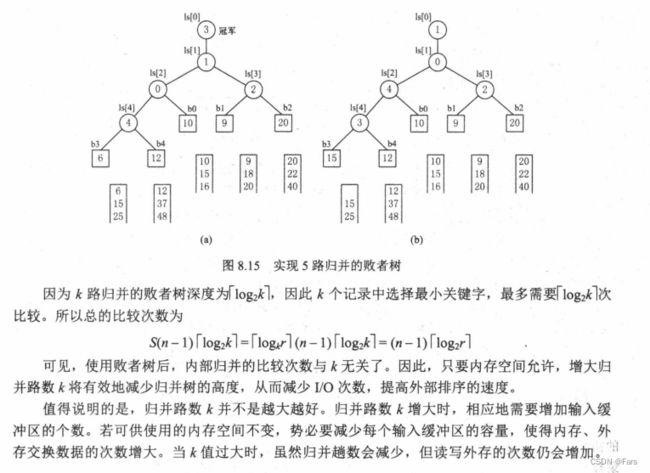
胜者树图
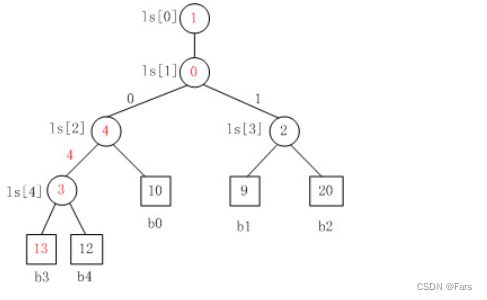
败者树图
败者树的具体实现,java代码
- 这个按照这个图顺序定义b0,b1~b4的顺序,b0必须从第一个最小叶子结点作为b0,才符合b_parnet = (b_index+b_size)/2
败者树的Java实现
参考败者树的Java实现_solari_bian的博客-CSDN博客
辅助数据结构Chunk与Record
Record就是Chunk流里面具体某个东西,这里以数值a作为排序依据
import java.io.Serializable;
/**
* 记录类,包含一个整数型属性A和一个字符串型属性B
*/
public class Record implements Serializable {
private int a;
private String b;
public Record(int a, String b) {
this.a = a;
this.b = b;
}
public int getA() {
return a;
}
public String getB() {
return b;
}
@Override
public String toString() {
return "Record{" +
"a=" + a +
", b='" + b + '\'' +
'}';
}
//写compareTo
public int compareTo(Record o) {
if (this.a > o.a) {
return 1;
} else if (this.a < o.a) {
return -1;
} else {
return 0;
}
}
}
Chunk就是通过置换-选择排序,得出来的一段已排序好的初始归并段
import java.util.ArrayList;
import java.util.List;
/**
* szf-lab2
*
*
* @author : Fars
* @date : 2023-04-27 23:31
**/
class Chunk{
public Chunk() {
}
public Chunk(int chunkId) {
this.chunkId = chunkId;
}
public Chunk(List recordList, int chunkId) {
this.recordList = recordList;
this.chunkId = chunkId;
}
private int chunkId =-1;//未赋值默认为-1
private List recordList = new ArrayList<>();
//实现add
public void add(Record record){
recordList.add(record);
}
//实现poll
public Record poll(){
return recordList.remove(0);
}
public List getRecordList() {
return recordList;
}
//实现getSize
public int getSize(){
return recordList.size();
}
//实现compareTo
public int compareTo(Chunk chunk){
Record record1 = this.recordList.get(0);
Record record2 = chunk.recordList.get(0);
return record1.compareTo(record2);
}
//实现isEmpty
public boolean isEmpty(){
return recordList.isEmpty();
}
@Override
public String toString() {
return "Chunk{" +
"chunkId=" + chunkId +
", recordList=" + recordList +
'}';
}
public int getChunkId() {
return chunkId;
}
} 败者树LoserTree,直接运行main即可
import javax.print.attribute.IntegerSyntax;
import java.util.ArrayList;
import java.util.List;
public class LoserTree
{
private int[] ls = null;// 以顺序存储方式保存所有非叶子结点
private int size = 0;
private ArrayList leaves = null;// 叶子节点
public LoserTree(ArrayList chunks)
{
this.leaves = chunks;// 叶子结点
this.size = chunks.size();// 叶子结点个数 = 块数 = ls个数
this.ls = new int[size];//ls个数 = 块数 = 叶子结点个数
for (int i = 0; i < size; ++i)
{
ls[i] = -1;
}
for (int i = size - 1; i >= 0; --i)
{
adjust(i);
}
}
/*
* @Description: 从chunks中删除第s块,并调整败者树
* @param s
* @return: void
* @Author: Fars
* @Date: 2023/4/27 23:28
*/
public void del(int s)
{
leaves.remove(s);
size--;
ls = new int[size];
for (int i = 0; i < size; ++i)
{
ls[i] = -1;
}
for (int i = size - 1; i >= 0; --i)
{
adjust(i);
}
}
public void add(Chunk leaf, int s)
{
leaves.set(s, leaf);// 调整叶子结点
adjust(s);// 调整非叶子结点
}
public Chunk getLeaf(int i)
{
return leaves.get(i);
}
public int getWinnerChunkIndex()
{
return ls[0];
}
public Chunk getWinnerChunk()
{
return leaves.get(ls[0]);
}
// public void adjust(int leafIndex)
// {
// // s指向当前的值最小的叶子结点(胜者)
// int parent = (leafIndex + size) / 2;// parent是leafIndex的双亲
//
// while (parent > 0)// 沿从叶子到根的路径比较,直到根结点
// {
// if (leafIndex >= 0 && (ls[parent] == -1 || leaves.get(leafIndex).compareTo(leaves.get(ls[parent])) > 0))
// {
// // 将树中的当前结点指向其子树中值最小的叶子
// int tmp = leafIndex;
// leafIndex = ls[parent];
// ls[parent] = tmp;
// }
// }
public void adjust(int leafIndex)
{
// s指向当前的值最小的叶子结点(胜者)
int parent = (leafIndex + size) / 2;// parent是leafIndex的双亲
while (parent > 0)// 沿从叶子到根的路径比较,直到根结点
{
int winnerIndex;
int loserIndex;
//如果是父节点ls[parent]为-1,代表还没有比赛过,应该要和兄弟比赛
if(ls[parent] == -1){
if (leaves.get(leafIndex).compareTo(leaves.get(leafIndex - 1)) < 0){
winnerIndex = leafIndex;
loserIndex = leafIndex - 1;
}
else{
winnerIndex = leafIndex - 1;
loserIndex = leafIndex;
}
}
//如果s战胜了父亲节点代表的leaf ( leave.get(s) < leaves.get(ls[parent]) ),那么胜者是s
else if(leaves.get(leafIndex).compareTo(leaves.get(ls[parent])) < 0){
winnerIndex= leafIndex;
loserIndex = ls[parent];
}
else{
winnerIndex = ls[parent];
loserIndex = leafIndex;
}
//将败者索引放到父亲节点
ls[parent] = loserIndex;
//将胜者继续向上比较
leafIndex = winnerIndex;
parent /= 2;
}
ls[0] = leafIndex;// 树根指向胜者
}
public static void main(String[] args) {
//给定示例输入数据
ArrayList chunks = new ArrayList();
Chunk chunk1 = new Chunk(0);
chunk1.add(new Record(1,"record_1"));
chunk1.add(new Record(7,"record_7"));
chunk1.add(new Record(8,"record_8"));
Chunk chunk2 = new Chunk(1);
chunk2.add(new Record(4,"record_4"));
chunk2.add(new Record(5,"record_5"));
chunk2.add(new Record(6,"record_6"));
chunks.add(chunk1);
chunks.add(chunk2);
//利用败者树排序
LoserTree loserTree = new LoserTree(chunks);
//输出排序结果
System.out.println("排序结果:");
while(true) {
System.out.println("当前winner代表的chunkIndex = " + loserTree.getWinnerChunkIndex());
System.out.println("该chunk = " + loserTree.getWinnerChunk().toString());
System.out.println("该chunk的块首元素 = " + loserTree.getWinnerChunk().poll());
int chunkIndex = loserTree.getWinnerChunkIndex();
Chunk winnerChunk = loserTree.getWinnerChunk();
//如果该chunk为空,则去除该chunk
if (loserTree.getWinnerChunk().isEmpty())
{
loserTree.del(chunkIndex);
System.out.println("删除chunk,其Id:" + winnerChunk.getChunkId());
if(chunks.size() == 0)
break;
}
else//否则调整败者树
loserTree.adjust(chunkIndex);
}
}
} 整个外部排序的模拟实现代码
有些许bug,应该无伤大雅
代码太多,就不放上来了,请看github
外部排序完整代码![]() https://github.com/944613709/external-sorting-of-k-way-multi-way-merge-sorting
https://github.com/944613709/external-sorting-of-k-way-multi-way-merge-sorting