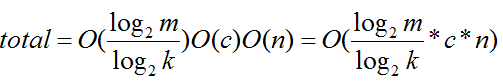外部排序——置换选择排序和败者树
外部排序
如果需要对大量的数据进行排序，且内存容量远小于数据量时，此时就需要用上外部排序了；一般外部排序分为两个步骤，第一阶段：生成初始归并段，第二阶段：递归的将这些初始归并段逐步合成一个大的有序排列；
生成初始归并段
生成初始归并段的方法有两种；
一、将数据分批读入内存，采用内部排序的方法，生成一个小的归并段，再写入外存。
ps:在从外存中读取数据时，每次尽可能读到内存容量满了了为止，这样生成的初始归并段的个数就会更少，第二个阶段归并的趟数也就小，总的I/O数也就会小，排序的速度就更快。
二、采用置换选择排序，初始时，从外存中读取一批数据写到内存，选择关键字最小的记录输出到外存，成为当前归并段的一部分，其空缺位置，由下一个输入数据代替，如果该数据的关键字比当前初始归并段中的最大的关键字据要小，那么将其做个标记，表示其不会参与生成当前归并段的比较过程(即在选择内存中的最小数据时，其将会被忽略)，它将等待生成下一个归并段时提供选择；否则，继续寻找最小值。反复进行上次操作，直到内存中的所有数据都被打上了标记，则当前归并段归并完成，即生成了一个初始归并段。接着生成下下一个归并段，直到全部数据都出路完毕。
示例：设输入文件的各个记录的关键字为
15，19，04，83，12，27，11，25，16，34，26，07，10，90，06，...
假设内存缓冲区可以容纳4个记录；生成归并段的过程如下图所示：用红色表示标记，在第一步时，选择关键字为04的记录输出，其位置有下一个输入代替，此时12比04要大，不需要标记，直接选取关键字最小的记录输出即可；第三步将关键字为15的记录输出时，此时下一个输入记录的关键字为11，比15要小，那么它就不能参与当全归并段的生成过程，于是就得做个标记；直到缓冲区中的所有关键字都被标记后，则当前初始归并段生成完成了。然后重复上述过程，生成下一个归并段，直到处理完所有 记录为止。
通过示例可以看到，采用方法二生成初始归并段中的记录数量不受内存容量限制，生成的初始归并段的数量更少，那么整个排序的过程就更快。另外一点值得注意的是，每次输入或输出的记录一般都是一批，而不会是单个，上述例子只是为方便说明。
递归的合成初始归并段
这里介绍两种方法，本质上都是k路归并；
一、以二路归并(即K=2)为例，类似于内部排序的归并算法；首先将内存分为三个部分，内存一用来存储从一个文件中读入的记录，内存二用来存储另一个文件中读取的记录，内容三用来存储当前内存中排序好的记录。具体做法如下：
假设将当前参与归并的文件编号为1，2；首先从文件1读取记录到内存1，直到内存1满了或者文件1中的记录全部读完了，文件2同理，只不过其中的记录存入内存2；然后依次比较内存1和内存2中的关键字大小，将小值依次存到内存3，当内存三满了之后，再将其中的内容输出到外存，此时，内存1或内存2中会有一部分空位置，在从相应的文件中读取记录将内存1、2填满或者直到文件读完，为了保证内存1、2中的记录依然有序，稍加处理即可，比如，在填满内存1,2之前，将其中的数据全部往前挪，直到对齐起始结点；然后在重复上述的比较过程过程，直到处理完文件1、2中的所有记录。
假设初始归并段的个数为m，总的记录个数为n,每次在内存中选择最小关键字时所花费的比较次数为c=k-1, k为归并的路数，那么第二阶段总的比较次数约为：
另外I/O也会影响排序的速度，所以总的排序时间等于I/O所花的时间加上在内存中比较所花费的时间； 上述方法的瓶颈在于k值的选取，如果k值过小，比较次数会减小，但相应的I/O次数会增大；如果k值过大，I/O数会较少，但比较次数会增大。由此可见，k值的选取非常关键，将上式进行简单的变形:
如果能够通过某种数据结构使得
那么相比于前一种方法，每趟选取最小关键字所需要的比较次数就更少，排序的速度肯定会加快；总的比较次数则可以变为：
此时，排序的速度与k值无关，而取决于I/O数。要想达到上述的效果，就得使用败者树了，通过它可以实现在选取最小关键字时，比较次数为
；这里得重复前面提到的，就是每一次读入内存的数据都是一批，而不会是一个，要不然就需要大量的I/O中断，那程序就很慢了。由于内存的容量的是有限的，所以k的选择是和内存容量相关的；归并路数k增大时，相应的需要增加输入缓冲区个数。如果可供应的内存不变，这将减少每个缓冲区的容量，使得内外存交换数据次数增大。所以k值过大时，虽然归并次数减少，但读写外存次数会增加。
二、败者树
败者树是一颗特殊的二叉树，其中的结点分为两种类型：
叶子结点：数据为记录类型。每个叶结点的值为从相应的有序子序列中读出的当前记录；
非叶子结点： 数据为整型，存储对应的叶子结点的序号，跟结点存储了最终的胜利者；
败者树的建立主要是两两比较的过程，如果比较的其中一方是叶结点，那么直接取出其上存储的记录即可，如果是非叶结点，那么得取出其指向的叶结点上存储的记录。
以下资料来自：https://blog.csdn.net/lsjseu/article/details/11708587?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2
败者树调整策略
（1）输入每个归并段的第一个记录作为归并树的叶子节点。建立初始化归并树。
（2）两两相比较，父亲节点存储了两个节点比较的败者（节点较大的值）；胜利者（较小者）可以参与更高层的比赛。这样树的顶端就是当次比较的冠军（最小者）。
（3）调整败者树，当我们把最小者输入到输出文件以后，需要从相遇的归并段取出一个记录补上去。补回来的时候，我们就需要调整归并树，我们只需要沿着当前节点的父亲节点一直比较到顶端。比较的规则是与父亲节点比较（父亲节点只是记录了一个败者索引，我们需要通过索引找到相应的值进行比较），比较小的（胜者）可以参与更高层的比较，即可以跟他爷爷比较，一直向上，直到根节点。比较大的（失败者）留在当前节点。
败者树编程(K路归并)
在实现利用败者树编程的时候，我们把败者树的叶节点和非叶点分开定义：
（1）叶节点存放在：b[k+1]，其中b[0..k-1]存放记录，b[k]存放了一个比所有记录一个最小值，表示虚节点，在初始化树的时候会用到。
（2）败者节点存放：ls[k]，ls[1...k-1]存放各次比较的败者数组索引。ls[0]存放了最后的冠军。
注意：这里每个叶节点都是连到非叶节点上的，这个叶节点就是我们的父节点，那我们怎么算出连到那个非叶节点上呢：通过t = (index + K)/2，得到我们父节点的索引t，这样我们在调整树的时候只需要比较b[ls[t]]，然后一直比较就行了。
（1）败者树创建
首先，是创建归并树，程序开始将ls[0...k-1]=K，表示第K+1（虚设）个归并段的记录当前最小。然后，我们从k-1到0，每次加入一个记录进行一次调整，算法自顶向下，直到所有记录加进来，归并树也就建好了。
#include
using namespace std;
#define K 5 //表示5路归并
#define MIN INT_MIN;
int b[K+1] = {17,5,10,39,15};
int ls[K] = {0};//记录败者的序号
void Adjust(int s)
{
for(int t=(s+K)/2; t>0; t=t/2){//t=(s+k)，得到与之相连ls数组的索引
if(b[s] > b[ls[t]])//父亲节点
{
int temp = s; //s永远是指向这一轮比赛最小节点
s = ls[t];
ls[t]=temp;
}
}
ls[0] = s;//将最小节点的索引存储在ls[0]
}
void CreateLoser()
{
b[K] = MIN;
int i;
for(i=0;i=0;i--)Adjust(i); //加入一个基点，要进行调整
}
int main()
{
CreateLoser();
system("pause");
return 0;
} 图示一下创建树的过程：
（2）归并排序
读入数据，创建归并树，判断b[ls[0]]==MAX,等于表示所有记录都已输出。不等于，输出当前冠军，然后从相应归并段读入数据填上。注意，如果相应的归并段已经空了，则填上MAX。下面给出伪代码：
void K_Merge()
{
for(int i=0;i(3)以下代码来自 http://blog.csdn.net/tiantangrenjian/article/details/6838491
#include
using namespace std;
#define LEN 10 //最大归并段长
#define MINKEY -1 //默认全为正数
#define MAXKEY 100 //最大值,当一个段全部输出后的赋值
struct Array
{
int arr[LEN];
int num;
int pos;
}*A;
int k,count;
int *LoserTree,*External;
void Adjust(int s)
{
int t=(s+k)/2;
int temp;
while(t>0)
{
if(External[s] > External[LoserTree[t]])
{
temp = s;
s = LoserTree[t];
LoserTree[t]=temp;
}
t=t/2;
}
LoserTree[0]=s;
}
void CreateLoserTree()
{
External[k]=MINKEY;
int i;
for(i=0;i=0;i--)Adjust(i);
}
void K_Merge()
{
int i,p;
for(i=0;i=A[p].num)External[p]=MAXKEY;
else
{
External[p]=A[p].arr[A[p].pos];
A[p].pos++;
}
Adjust(p);
}
cout<>k;
A=(Array *)malloc(sizeof(Array)*k);
for(i=0;i>A[i].num;
count=count+A[i].num;
for(j=0;j>A[i].arr[j];
}
A[i].pos=0;
}
LoserTree=(int *)malloc(sizeof(int)*k);
External=(int *)malloc(sizeof(int)*(k+1));
K_Merge();
return 0;
}
参考资料：
1.https://blog.csdn.net/lsjseu/article/details/11708587?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-2
2.https://blog.csdn.net/tiantangrenjian/article/details/6838491
3.天勤计算机考研高分笔记——数据结构