【论文笔记】DiffBEV: Conditional Diffusion Model for Bird’s Eye View Perception
原文链接:https://arxiv.org/abs/2303.08333
1. 引言
通常,相机参数和激光雷达扫描的噪声会使BEV特征带有有害的噪声。扩散模型有去噪能力,能将有噪声样本还原为理想数据。本文提出DiffBEV,使用条件扩散概率模型(DPM)提高BEV特征的质量。然后,交叉注意力会融合条件扩散模型的输出与原始BEV特征。
DiffBEV可以接入不同的下游任务分支,并进行端到端的训练。
3. 方法
3.1 概述
如下图所示,本文的模型分为图像视图主干、视图变换器、条件扩散模型、交叉注意力和任务相关的解码器。

实际实施时,使用LSS作为默认的视图变换器。
3.2 条件扩散概率模型
3.2.1 扩散概率模型
本文将视图变换器的输出特征作为扩散模型的条件。设 x T x_T xT为服从标准正态分布 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)的噪声,扩散模型逐步地将 x T x_T xT转换为原始样本 x 0 x_0 x0。将第 t ( 0 ≤ t ≤ T ) t(0\leq t\leq T) t(0≤t≤T)步的方差记为 β t \beta_t βt。
条件扩散概率模型的前向过程如下: q ( x t ∣ x t − 1 ) ∼ N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t|x_{t-1})\sim\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI) q(xt∣xt−1)∼N(xt;1−βtxt−1,βtI) 记 α t = 1 − β t , α ˉ t = ∏ s = 1 t α s \alpha_t=1-\beta_t,\bar{\alpha}_t=\prod_{s=1}^t\alpha_s αt=1−βt,αˉt=∏s=1tαs。则第 t t t步的带噪声样本 q ( x t ∣ x 0 ) ∼ N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) x t ∼ α ˉ t x 0 + 1 − α ˉ t ϵ q(x_t|x_0)\sim\mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0,(1-\bar{\alpha}_t)I)\\x_t\sim\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\epsilon q(xt∣x0)∼N(xt;αˉtx0,(1−αˉt)I)xt∼αˉtx0+1−αˉtϵ其中 ϵ ∼ N ( 0 , I ) \epsilon\sim\mathcal{N}(0,I) ϵ∼N(0,I)。
去噪过程逐步地修正带噪声样本 x t x_t xt。逆过程可记为: p θ ( x t − 1 ∣ x t ) ∼ N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) p_\theta(x_{t-1}|x_t)\sim\mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t)) pθ(xt−1∣xt)∼N(xt−1;μθ(xt,t),Σθ(xt,t))其中 Σ θ ( x t , t ) \Sigma_\theta(x_t,t) Σθ(xt,t)是协方差预测器、 ϵ θ ( x t , t ) \epsilon_\theta(x_t,t) ϵθ(xt,t)是去噪模型。本文使用U-Net的典型变体作为去噪模型。
3.2.2 条件的设计
有3个可选的条件类型:(1)视图变换器输出的原始BEV特征 F O − B E V ∈ R C × H × W F^{O-BEV}\in\mathbb{R}^{C\times H\times W} FO−BEV∈RC×H×W;(2)从深度分布中学到的语义特征 F S − B E V ∈ R C × H × W F^{S-BEV}\in\mathbb{R}^{C\times H\times W} FS−BEV∈RC×H×W;(3) F O − B E V F^{O-BEV} FO−BEV和 F S − B E V F^{S-BEV} FS−BEV的和。
视图变换器会预测深度分布 F d ∈ R c × h × w F^d\in\mathbb{R}^{c\times h\times w} Fd∈Rc×h×w。使用 1 × 1 1\times1 1×1卷积转换通道数并将 F d F_d Fd插值为 F S − B E V F^{S-BEV} FS−BEV,使其与 F O − B E V F^{O-BEV} FO−BEV有相同尺寸。
上面这一步不太清楚, h , w h,w h,w是图像的长和宽吗?如果是的话,如何通过插值从图像视图的特征得到BEV下的特征?
本文希望通过逐步对样本去噪,条件扩散模型能帮助学习到物体细粒度的内容,如精确的边界和高细节的形状。对条件加噪声时,与标准的DPM相同;但在去噪时,使用了条件调制的去噪,如前图所示。
在第 t t t步,给定有噪声BEV特征 x t x_t xt和条件 x c o n d x_{cond} xcond, x t x_t xt被进一步编码并通过按元素乘法与 x c o n d x_{cond} xcond交互。
3.3 交叉注意力
得到条件扩散模型的输出后,设计交叉注意力修正原始BEV特征,如下图所示。
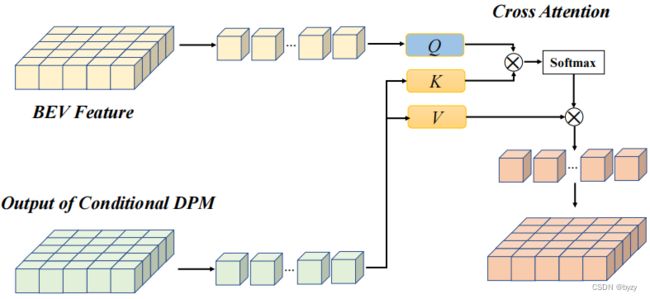
条件扩散模型的输出作为 K K K和 V V V,原始BEV特征为 Q Q Q。公式为 C A ( Q , K , W ) = A t t n ( Q W i Q , K W i K , V W i V ) W O u t A t t n ( Q , K , V ) = softmax ( Q K T d k ) V CA(Q,K,W)=Attn(QW^Q_i,KW^K_i,VW^V_i)W^{Out}\\Attn(Q,K,V)=\text{softmax}(\frac{QK^T}{\sqrt{d_k}})V CA(Q,K,W)=Attn(QWiQ,KWiK,VWiV)WOutAttn(Q,K,V)=softmax(dkQKT)V
3.4 训练损失
深度损失。给定内参矩阵 K i ∈ R 3 × 3 K_i\in\mathbb{R}^{3\times3} Ki∈R3×3,旋转矩阵 R i ∈ R 3 × 3 R_i\in\mathbb{R}^{3\times3} Ri∈R3×3和平移矩阵 t i ∈ R 3 t_i\in\mathbb{R}^3 ti∈R3,引入深度损失 L d e p t h \mathcal{L}_{depth} Ldepth辅助训练。使用二元交叉熵(BCE)损失。记预测深度图为 D i D_i Di,则深度损失如下: P i = K i ( R i P + t i ) , D i ∗ = o n e _ h o t ( P i ) , L d e p t h = BCE ( D i ∗ , D i ) P_i=K_i(R_iP+t_i),D^*_i=one\_hot(P_i),\mathcal{L}_{depth}=\text{BCE}(D_i^*,D_i) Pi=Ki(RiP+ti),Di∗=one_hot(Pi),Ldepth=BCE(Di∗,Di)这里 P P P是激光点云里点的坐标, P i P_i Pi是其在第 i i i个视图图像上的投影坐标,one_hot只处理深度维度。
扩散损失。设第 t t t步的高斯噪声为 z ˉ t \bar{z}_t zˉt,则扩散损失为 L d i f f = E [ ∥ z ˉ t − Σ θ ( α ˉ t x 0 + 1 − α ˉ t z ˉ t , t ) ∥ 2 ] \mathcal{L}_{diff}=\mathbb{E}[\|\bar{z}_t-\Sigma_\theta(\sqrt{\bar{\alpha}_t}x_0+\sqrt{1-\bar{\alpha}_t}\bar{z}_t,t)\|^2] Ldiff=E[∥zˉt−Σθ(αˉtx0+1−αˉtzˉt,t)∥2]
任务损失。总的损失为BEV分割损失/检测损失与深度损失、扩散损失的加权和。
3.5 任务解码器
BEV分割头使用残差网络;检测头使用CenterPoint的检测头。
4. 实验
4.3 BEV语义分割
LSS对覆盖范围广的静态目标分割准确,因为动态目标通常较小,且出现频率低。
DiffBEV对静态和动态物体的分割均有显著的性能提升,这是由于DPM能减小噪声并为感兴趣的物体补充更多的空间信息。
4.4 3D目标检测
引入条件扩散模型后,所有指标均有提升。这是因为模型能逐步精炼原始BEV特征,并通过交叉注意力交互式地交换语义上下文。
4.5 消融研究
4.5.1 条件设计
对静态道路进行分割的实验表明,使用不同的条件均能引导模型获取有判别力的BEV特征。其中使用 F S − B E V F^{S-BEV} FS−BEV的性能最好, F O − B E V F^{O-BEV} FO−BEV的性能则相对最差。
4.5.2 特征交互机制
本文比较了三种特征交互机制,即拼接、求和和交叉注意力。
使用交叉注意力能学到更好的BEV特征,从而有利于下游感知任务。综合考虑条件设计和特征交互机制,使用 F S − B E V F^{S-BEV} FS−BEV和交叉注意力组合的性能是最优的。
4.5.3 带噪声BEV样本的编码机制
在条件扩散模型中,对有噪声BEV样本 x t x_t xt,本文考虑两种编码方式:(1)计算其自注意力语义图;(2)通过卷积获取细化亲和性图(affinity map)。使用前者有更好的性能,但后者的计算负担小。
4.6 更多的视图变换器
将LSS替换为其他的视图变换器进行实验,可发现与不带扩散模型的原始方法相比,DiffBEV均有更高的性能。
4.7 可视化分析
可视化表明,DiffBEV能提供更精确的语义图,且能解决细粒度的细节(如相邻车辆之间的分离、静态道路的清晰边界)。
补充材料
A. 训练损失
A.1 分割损失
对于 M M M个类别的语义分割,训练损失可分解为 M M M个加权二分类损失: L w c e = ∑ c = 1 M w c N p o s [ − ∑ i = 1 N p o s y i log p c i − ∑ i = 1 N n e g ( 1 − y i ) log ( 1 − p c i ) ] \mathcal{L}_{wce}=\sum_{c=1}^M\frac{w_c}{N_{pos}}[-\sum_{i=1}^{N_{pos}}y_i\log p_{ci}-\sum_{i=1}^{N_{neg}}(1-y_i)\log(1-p_{ci})] Lwce=c=1∑MNposwc[−i=1∑Nposyilogpci−i=1∑Nneg(1−yi)log(1−pci)]其中 p c i p_{ci} pci是每个像素预测的分类置信度, w c w_c wc是根据类别分布计算的类别权重。 y i y_i yi表示像素的语义标签。 N p o s N_{pos} Npos和 N n e g N_{neg} Nneg为正负样本的数量。