树形DP例题
目录
一.什么是树形DP?
二.树形DP例题
三.总结
一.什么是树形DP?
简单来说,树形DP就是在树结构上进行状态转移的一种思想。一般是根据子树的状态更新父亲的状态,进行状态转移,跟分治的思想非常像。
二.树形DP例题
1.树的最长路径
(1)题意分析:首先树有一个很重要的性质:树上任意点能到的最远点,一定是树的直径的某个端点,因此本题就是让我们求树的直径。因此我们只需要知道以某个点向其他方向的最远距离 + 某个点向下的最远距离,就可以知道树的直径是多少。
(2)解题思路: 对于求向下最远距离,我们只需要dfs算出深度就可以了,那么如何求解其他方向的最远距离呢?对于这个问题,我们看树上直径的图,实际上会是一条链。
比如说这个图,我们能明显看出来,这条直径一定是通过某个点挂起来的,就像那种晒衣架一样,我们只需要保证对于某个点不经过重复的一颗子树获得的最大的距离和次大距离,则一定是以这个点其他方向或者向下扩展了,则此时答案就是最大距离和最小距离的和。
(3)代码实现:
#include "bits/stdc++.h"
using namespace std;
struct node{
int nxt;
int to;
int wi;
}e[20010];
int idx,he[10010],ans = -1e9;
void add(int u,int v,int w)
{
e[++idx].nxt = he[u];
e[idx].to = v;
e[idx].wi = w;
he[u] = idx;
}
int dfs(int cur,int fa)
{
int d1 = 0,d2 = 0,dis = 0;
for(int i = he[cur];~i;i = e[i].nxt){
if(e[i].to == fa) continue;
int d = dfs(e[i].to,cur) + e[i].wi;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
dis = max(d,dis);
}
ans = max(d1 + d2,ans);
return dis;
}
void init(int n)
{
for(int i = 1;i <= n;i++) he[i] = -1;
}
int main()
{
int n,u,v,w;
cin >> n;
init(n);
for(int i = 1;i < n;i++) {
cin >> u >> v >> w;
add(u,v,w);add(v,u,w);
}
dfs(1,-1);
cout << ans << endl;
return 0;
}2.树的中心(换根DP)
题意分析:此题给定我们一颗树,让我们求树中一个点到其他点的最远距离最近,也就是中心。
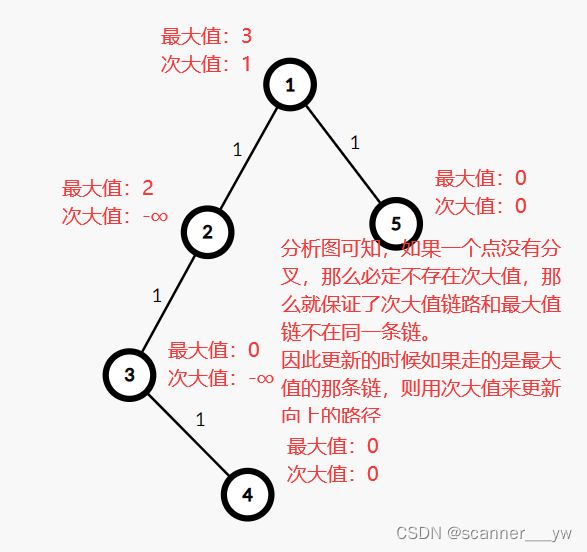
这个题的做法和上个题非常类似,是以一个点为中心,往上和往下遍历,找到最远的距离。因此我们需要向下dfs一遍,向上dfs一遍求出最远距离。对于向下求解最远距离,我们利用父节点信息更新子节点信息即可;对于向上求解最远距离,我们利用子节点更新父亲节点的信息即可。(注意:当我们向上dfs的时候,如果发现当前节点在父亲节点的最长路径里面,那么就不能用当前节点的最大值去更新父亲节点,而应当用次大值去更新父亲节点的信息。
图解:
代码实现:
#include "bits/stdc++.h"
using namespace std;
struct node{
int nxt;
int to;
int wi;
}e[20010];
int idx,he[10010],ans = -1e9;
void add(int u,int v,int w)
{
e[++idx].nxt = he[u];
e[idx].to = v;
e[idx].wi = w;
he[u] = idx;
}
int dfs(int cur,int fa)
{
int d1 = 0,d2 = 0,dis = 0;
for(int i = he[cur];~i;i = e[i].nxt){
if(e[i].to == fa) continue;
int d = dfs(e[i].to,cur) + e[i].wi;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
dis = max(d,dis);
}
ans = max(d1 + d2,ans);
return dis;
}
void init(int n)
{
for(int i = 1;i <= n;i++) he[i] = -1;
}
int main()
{
int n,u,v,w;
cin >> n;
init(n);
for(int i = 1;i < n;i++) {
cin >> u >> v >> w;
add(u,v,w);add(v,u,w);
}
dfs(1,-1);
cout << ans << endl;
return 0;
} 3.数字转换 
题意:这个题让我们首先处理一个树的约数,如果一个数的约数和小于他本身的话,那么就会存在一条约数和----->他本身的路径,最后我们建立树模型求解一个最长直径就可以了。(我们求解最长直径的时候,以1为根节点进行搜索,因为对于任何一个数,如果他是质数,那么他的约数和必定是一,因此一定挂在1这个根节点上;如果这个数是个合数,那么他一定能分解成为质数相乘,必定会挂在质数上面,因此一定会挂在1这棵树上。
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 50010;
struct node{
int nxt;
int to;
}e[N];
int he[N],sum[N],cnt,ans;
void add(int a,int b)
{
e[++cnt].nxt = he[a];
e[cnt].to = b;
he[a] = cnt;
}
int dfs(int u)
{
int d1 = 0,d2 = 0;
for(int i = he[u];~i;i = e[i].nxt) {
int to = e[i].to;
int d = dfs(to) + 1;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
}
ans = max(ans,d1 + d2);
return d1;
}
int main()
{
int n;
cin >> n;
memset(he,-1,sizeof(he));
for(int i = 1;i <= n;i++) {
for(int j = 2;j <= n / i;j++) {
sum[i * j] += i;
}
}
for(int i = 2;i <= n;i++) if(sum[i] < i) add(sum[i],i);
dfs(1);
cout << ans << endl;
return 0;
}4.二叉苹果树

题意:给定你n个数,n-1条边,q个点,问你保留q个点的最大价值为多少。我们可以拟定如果下dp数组,dp[i][j]为以i点为根节点,保留j个节点的最大价值是多少。又因为对于每一个节点我们想要保留他这个节点,那么一定会保留他的父亲节点。因此这是一个树上的分组背包问题。
故状态转移方程为dp[i][j] = max(dp[i][j],dp[i][j - k - 1][j] + e[i].wi + dp[son][k])
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 110;
struct node{
int nt;
int to;
int wi;
}e[N << 1];
int dp[N][N],he[N],cnt;
int m,n;
void add(int a,int b,int c)
{
e[++cnt].nt = he[a];
e[cnt].to = b;
e[cnt].wi = c;
he[a] = cnt;
}
//acwing1074
//类似于有依赖的背包,首先枚举子树(物品组),然后枚举操作数(体积),最后枚举选择(决策)
void dfs(int u,int fa)
{
for(int i = he[u];~i;i = e[i].nt){
int son = e[i].to;
if(son == fa) continue;
dfs(son,u);
for(int j = m;j >= 1;j--){
for(int k = 0;k < j;k++) {
dp[u][j] = max(dp[u][j],dp[u][j - k - 1] + e[i].wi + dp[son][k]);
}
}
}
}
int main()
{
cin >> n >> m;
memset(he,-1,sizeof(he));
for(int i = 1;i < n;i++) {
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
add(b,a,c);
}
dfs(1,-1);
cout << dp[1][m] << endl;
return 0;
}5.战略游戏
题意:对于每一个节点我们都能够放置一个守卫,可以看他与他连边的所有点,问我们整棵树的所有点互相能看到最少需要放置多少个守卫。
对于这个题目,我们拟定状态转移数组为dp[i][j],表达以i为根,j有两个状态(0,1), 表示我当前放置守卫和不放置守卫的。
那么对于这个转移状态可以表示为
1.如果我当前节点不放守卫,那么我的连边节点必须放置守卫。
dp[i][0] += dp[son][1];
2.如果我们当前节点放置守卫,那么我们子节点可以放置守卫,也可以不放置守卫。
dp[i][1] += min(dp[son][0],dp[son][1]);
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 1510;
struct node{
int nt;
int to;
}e[N << 1];
int dp[N][N],he[N],idx,vs[N],n;
//战略游戏acwing323
void add(int a,int b)
{
e[++idx].to = b;
e[idx].nt = he[a];
he[a] = idx;
}
void dfs(int cur)
{
dp[cur][0] = 0;
dp[cur][1] = 1;
for(int i = he[cur];~i;i = e[i].nt) {
int to = e[i].to;
dfs(to);
dp[cur][0] += dp[to][1];
dp[cur][1] += min(dp[to][0],dp[to][1]);
}
}
int main()
{
while(scanf("%d",&n) != -1) {
int p,cnt,x;
idx = 0;
memset(he,-1,sizeof(he));
memset(vs,0,sizeof(vs));
for(int k = 1;k <= n;k++){
scanf("%d:(%d)",&p,&cnt);
for(int i = 1;i <= cnt;i++) {
scanf("%d",&x);
add(p,x);
vs[x] = 1;
}
}
int root = 0;
for(int i = 0;i < n;i++) if(!vs[i]) root = i;
dfs(root);
printf("%d\n",min(dp[root][1],dp[root][0]));
}
return 0;
}6.皇宫看守
题意:该题和上题不一样的是,我们各个节点不需要相互看到,只需要最小覆盖到整棵树就可以了。因此对于状态方程的思考,我们还需要考虑多一个状态,那就是当前节点不放置守卫,后面节点放置守卫看到当前节点的最小价值是多少。
我们定义dp[i][j](j分别为0,1,2),
0表示当前节点被父亲节点看到了
1表示当前节点被子节点看到了
2表示当前节点放置守卫
1.对于当前节点被父亲节点看到
状态方程为:dp[i][0] += min(dp[son][1],dp[son][2]);
2.对于当前节点被子节点看到了
状态方程为:min(dp[i][1],dp[son][2] + dp[i][0] - min(dp[son][1],dp[son][2]));
3.对于当前节点放置守卫
状态方程为:dp[i][j] += min({dp[son][0],dp[son][1],dp[son][2]})
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 1510;
struct node{
int nt;
int to;
}e[N << 2];
int he[N],w[N],idx,dp[N][N];
bool vs[N];
void add(int a,int b)
{
e[++idx].to = b;
e[idx].nt = he[a];
he[a] = idx;
}
void dfs(int u)
{
//在自己这里摆放侍卫
dp[u][2] = w[u];
for(int i = he[u]; ~i;i = e[i].nt) {
int j = e[i].to;
dfs(j);
//dp[u][0]表示被父节点看到了,那么当前节点就不需要摆放侍卫,子节点是否摆放无所谓
dp[u][0] += min(dp[j][1],dp[j][2]);
//dp[u][2]表示自己这个点放一个侍卫,那么子节点可以被父节点看到,也可以自己摆放,也可以被子节点的子节点看到
dp[u][2] += min({dp[j][0],dp[j][1],dp[j][2]});
}
//dp[u][1] 表示u点被子节点看到
dp[u][1] = 1e9 + 10;
for(int i = he[u]; ~i;i = e[i].nt) {
int j = e[i].to;
//被子节点看到时,我们要拿所有子节点的摆放值减去当前子节点被看到的最小值,然后加上当前子节点自己摆放侍卫的值
dp[u][1] = min(dp[u][1],dp[j][2] + dp[u][0] - min(dp[j][1],dp[j][2]));
}
}
int main()
{
int n,root = 1;
cin >> n;
memset(he,-1,sizeof(he));
for(int i = 1;i <= n;i++) {
int id,cnt,wi,x;
cin >> id >> wi >> cnt;
w[id] = wi;
for(int j = 1;j <= cnt;j++){
cin >> x;
add(id,x);
vs[x] = true;
}
}
while(vs[root]) root++;
dfs(root);
cout << min(dp[root][1],dp[root][2]) << endl;
return 0;
}7.Educational Codeforces Round 136 (Rated for Div. 2)D
(1)题意分析
给定一颗树,我们最多可以做k次操作,每一次操作我们可以把这颗子树连到根节点上去,现在问我们k次操作后,树中最大高度的子树最小是多少?
(2)解题思路
我们可以二分答案,然后看变成这个高度是否可以小于等于k次操作,显然我们check的时候可以用树形dp,对于某一个子树,若子树中最大的高度减去当前最大高度等于mid了,那么我们就要杨掉这颗子树,cnt++,否则就要更新当前树最大子树高度。
(3)代码实现
#include "bits/stdc++.h"
using namespace std;
const int N = 2e5 + 10;
vector e[N];
int f[N],dep[N];
int n,k,mx,cnt;
void dfs(int u)
{
for(auto x:e[u]) {
dep[x] = dep[u] + 1;
dfs(x);
}
}
void dp(int u,int mid)
{
f[u] = dep[u];
for(auto x:e[u]) dp(x,mid);
if(u == 1) return;
for(auto x:e[u]) {
if(f[x] - dep[u] == mid) cnt ++;
else f[u] = max(f[x],f[u]);
}
}
void solve()
{
int x;
cin >> n >> k;
for(int i = 1;i <= n;i++) e[i].clear();
for(int i = 2;i <= n;i++) {
cin >> x;
e[x].push_back(i);
}
memset(dep,0,sizeof(dep));
dfs(1);
int l = 1,r = n;
while(l <= r) {
int mid = (l + r) >> 1;
cnt = 0;dp(1,mid);
if(cnt <= k) r = mid - 1;
else l = mid + 1;
}
cout << l << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T;
cin >> T;
while(T --) {
solve();
}
return 0;
} 8.Problem - D - Codeforces
(1)题目大意
给你一颗以一为根的树,树上每个点都有一个自己的权值,现在给你一个k,对于每一次你可以把k分给下一层,必须保证下一层的所有节点的权值不能相差超过1,记分给每个点的权值为ci,
本身权值为vi,这颗树的价值为![]() ,问你这棵树最大价值是多少。
,问你这棵树最大价值是多少。
(2)解题思路
考虑到每颗子树可能分配多1或者不多的局面,我们把不多的局面加上最大的能多1的局面的前k/siz个,就是这棵子树的价值,最后答案就是f[1][k];
(3)代码实现
#include "bits/stdc++.h"
using namespace std;
const int N = 2e5 + 10;
map f[N];
int v[N];
vector G[N];
long long dfs(int u,int k)
{
if(f[u].count(k)) return f[u][k];
if(k == 0) return f[u][k] = 0;
vector cost;
int siz = G[u].size();
long long ans = 1LL * k * v[u];
if(siz == 0) return f[u][k] = ans;
for(auto x:G[u]) {
cost.push_back(dfs(x,(k + siz - 1) / siz) - dfs(x,k / siz));
ans += f[x][k / siz];
}
if(k % siz) {
sort(cost.rbegin(),cost.rend());
for(int i = 0;i < k % siz;i++) ans += cost[i];
}
return f[u][k] = ans;
}
void solve()
{
int n,k,u;
scanf("%d%d",&n,&k);
for(int i = 1;i <= n;i++) {
G[i].clear();
f[i].clear();
}
for(int i = 2;i <= n;i++) {
scanf("%d",&u);
G[u].push_back(i);
}
for(int i = 1;i <= n;i++) scanf("%d",&v[i]);
printf("%lld\n",dfs(1,k));
}
int main()
{
int T;
scanf("%d",&T);
while(T --) solve();
return 0;
}