【数据结构】二叉树链式结构补充和二叉树的顺序结构及实现
博客主页： 云曦
系列专栏：数据结构吾生也有涯，而知也无涯 感谢大家点赞 关注评论
文章目录
- 前言
- 一、二叉树链式结构的接口补充
-
- 1.1 二叉树第k层节点的个数
- 1.2 二叉树查找值为x的节点
- 1.3 判断一颗二叉树是否是完全二叉树
- 二、二叉树的顺序结构
-
- 2.1 二叉树顺序结构的概念
- 2.2 堆实现
-
- 2.2.1 堆的初始化
- 2.2.2 堆的销毁
- 2.2.3 堆的插入
-
- 2.2.3.1 向上调整算法
- 2.2.4 堆的删除
-
- 2.2.4.1 向下调整算法
- 2.2.5 获取堆顶元素
- 2.2.6 检测堆是否为空
- 2.3 堆排序
- 2.4 TOPK问题
- 2.5本篇章的代码
前言
上一期讲到了二叉树的链式结构，但上一期的链式结构还差着几个接口没写，所以在这一期补上，然后就是二叉树的顺序结构讲解了，二叉树的顺序结构将会实现堆和堆排序，最后会用堆实现TOPK问题。
一、二叉树链式结构的接口补充
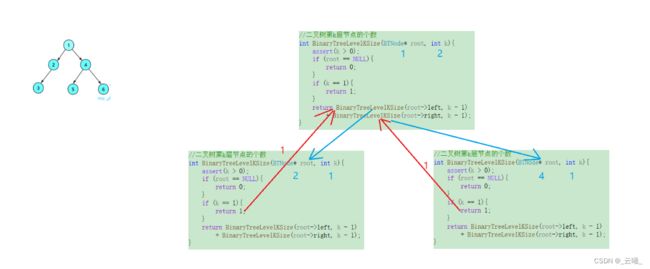
1.1 二叉树第k层节点的个数
- 思路：递归左右子树并且相加，层层进入且每次进入k都减1，当k等于1时就是第k层，然后返回1给上一层。
- 需要注意的是，传入的k有可能小于0，所以要检查一下k
int BinaryTreeLevelKSize(BTNode* root, int k)
{
assert(k > 0);//检测k是否小于0
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return BinaryTreeLevelKSize(root->left, k - 1)
+ BinaryTreeLevelKSize(root->right, k - 1);
}
此接口的递归展开图
1.2 二叉树查找值为x的节点
- 思路：遍历找到k节点，但找到了返回也只是返回到上一层的函数栈帧的执行位置，所以解决方法就是，定义一个节点接收回归的值，然后判断这个节点是否等于或不等于NULL，需要注意的是左右子树都要判断一下，因为有可能要找的节点不在左子树，在右子树里。
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
BTNode* ret = NULL;
ret = BinaryTreeFind(root->left, x);
if (ret)
{
return ret;
}
ret = BinaryTreeFind(root->right, x);
if (ret)
{
return ret;
}
return NULL;
}
1.3 判断一颗二叉树是否是完全二叉树
- 思路：跟层序遍历的思路差不多，只是这里要把NULL也入队列，然后出队列时，等于NULL就跳出循环，然后再循环出队列的数据。
- 如果有不等于NULL的节点，那么这颗树就不是完全二叉树。
- 遍历一遍后，没有返回，那么这棵树就是完全二叉树。
bool BinaryTreeComplete(BTNode* root)
{
//创建及初始化队列
Que q;
QueueInit(&q);
//把根不等于空(NULL)时入队列
if (root)
{
QueuePush(&q, root);
}
//思路：上一层出带下一层进
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);
//当节点等于空时，break跳出循环
if (Front == NULL)
{
break;
}
//NULL也入队列
QueuePush(&q, Front->left);
QueuePush(&q, Front->right);
QueuePop(&q);
}
//继续出队列，此时如果遇到不等于空(NULL)的节点
//那么这颗树就不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* Front = QueueFront(&q);
QueuePop(&q);
if (Front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
//到这里时，已经遍历完整棵树了，此时这棵树就是完全二叉树
return true;
}
二、二叉树的顺序结构
2.1 二叉树顺序结构的概念
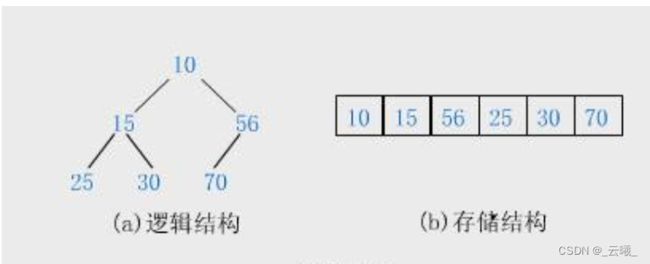
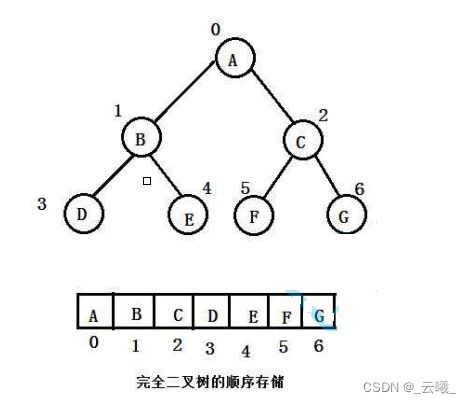
- 概念：普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统
虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段- 堆的逻辑结构是一颗完全二叉树，但物理结构是一个数组
- 堆又分为小根堆(小堆)或大根堆(大堆)
- 小堆：这颗完全二叉树的所有父亲节点的数据都小于孩子节点
- 大堆：这颗完全二叉树的所有父亲节点的数据都大于孩子节点
- 查找一颗完全二叉树的父亲或左右孩子的方法:
- leftchild = parent * 2 + 1（左孩子 = 父亲乘2加1）
- right = parent * 2 + 2 （右孩子 = 父亲乘2加2）
- parent = (child - 1) / 2 (父亲 = (孩子-1) / 2)
- 堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树。
- 堆的结构
typedef int HPDataType;
typedef struct Heap
{
HPDataType* arr;
int size;
int capacity;
}HP;
2.2 堆实现
- 堆其实是用顺序表实现的，只是逻辑结构与顺序表有些差异
2.2.1 堆的初始化
- 堆的初始化有两种结构
- 第一种结构：
void HeapInit(HP* php)
{
assert(php);
php->arr = NULL;
php->capacity = 0;
php->size = 0;
}
- 第二种结构：
这种结构其实就是，给一个n个元素的数组，让我们把数组的数据拷贝到堆里然后建堆
void HeapInitArray(HP* php, HPDataType* arr, int n)
{
assert(php);
assert(arr);
//开辟n个空间
php->arr = (HPDataType*)malloc(sizeof(HPDataType)*n);
if (php->arr == NULL)
{
perror("malloc fail");
exit(-1);
}
php->capacity = n;
php->size = n;
//把原数组的数据拷贝到在堆上开辟的数组里
memcpy(php->arr, arr, sizeof(HPDataType) * n);
//向上调整建堆
int i = 0;
for (i = 1; i < n; i++)
{
AdjustUp(php->arr, i);
}
}
2.2.2 堆的销毁
堆的销毁跟顺序表一样的，释放开辟的空间，然后把容量和有效数据的个数置为0
void HeapDestroy(HP* php)
{
assert(php);
free(php->arr);
php->arr = NULL;
php->capacity = 0;
php->size = 0;
}
2.2.3 堆的插入
- 把扩容的功能实现出来
//容量满了，扩容
if (php->size == php->capacity)
{
int newCapacity = php->capacity == 0 ?
INIT_SIZE : php->capacity * TIMES;
HPDataType* tmp=(HPDataType*)realloc(php->arr,
sizeof(HPDataType) * newCapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->arr = tmp;
php->capacity = newCapacity;
}
- 然后把插入数据
php->arr[php->size] = x;
php->size++;
- 插入数据后，把数据向上调整，让这个数组变成堆
AdjustUp(php->arr, php->size-1);
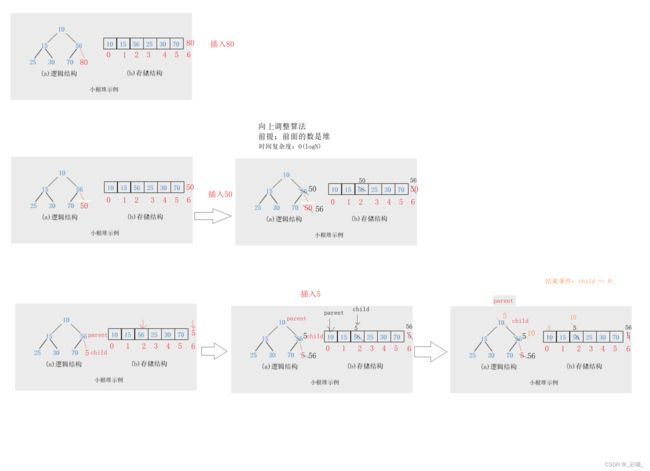
2.2.3.1 向上调整算法
- 注意：向上调整算法的前提是：前面的数是堆
- 接收数组和插入数据的位置(n-1的位置)
- 计算父亲的位置，公式为：parent = (child - 1) / 2
- 让孩子和父亲比较，小于父亲就交换孩子和父亲的位置
- 然后把父亲的下标赋值给孩子，再计算父亲的位置
- 如果孩子大于父亲，那么就break跳出循环
- 时间复杂度：O(logN)
void AdjustUp(int* arr, int child)
{
int parent = (child - 1) / 2;//计算父亲的位置
//child等于0时，为循环结束的条件
while (child > 0)
{
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);//交换函数
child = parent;
parent = (child - 1) / 2;
}
else
{
//孩子大于父亲时跳出循环
break;
}
}
}
- 测试：
int main()
{
int arr[] = { 65,100,70,32,50,60 };
HP hp;
HeapInit(&hp);
int i = 0;
for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
HeapPush(&hp, arr[i]);
}
HeapPrint(&hp);
HeapDestroy(&hp);
return 0;
}
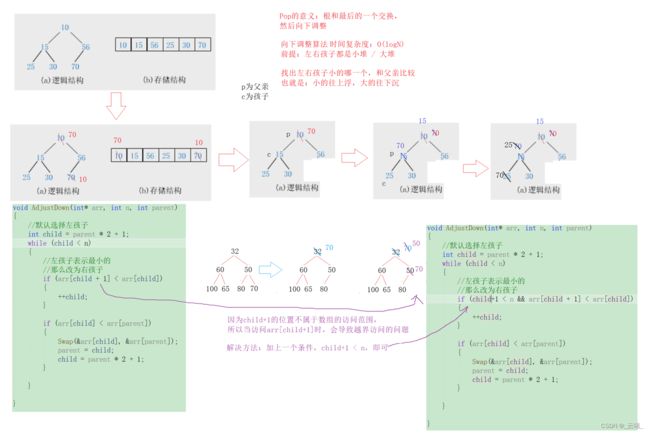
2.2.4 堆的删除
堆的删除，删尾没有任何意义，但把首尾元素交换一下，那么每次删除的都是最小/最大的元素，配合获取堆顶元素的接口，可以实现排序了
思路：
- 先将首尾元素交换
- size减1
- 最后向下调整建堆，向下调整只影响尾元素的祖先，不会影响其他的元素
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
//交换首尾的数据
Swap(&php->arr[0], &php->arr[php->size - 1]);
php->size--;
//然后向下调整
AdjustDown(php->arr, php->size, 0);
}
2.2.4.1 向下调整算法
- 向下调整的前提是：左右孩子都是小堆 / 大堆
- 先找出左右孩子最小的哪一个，那么就要计算孩子的位置，但这里有个小技巧，先默认左孩子是最小的，然后再判断，如果右孩子小于左孩子child就加1变成右孩子
- 此时，左右孩子谁小我们不关心，判断孩子是否小于父亲，孩子小于父亲，那么就交换孩子和父亲的位置，把孩子的下标赋值给父亲，再计算孩子的下标
- 孩子大于父亲，就证明堆建好了，break跳出循环
- 时间复杂度：O(logN)
void AdjustDown(int* arr, int n, int parent)
{
//默认选择左孩子
int child = parent * 2 + 1;
while (child < n)
{
//左孩子表示最小的
//那么改为右孩子
if (child+1 < n && arr[child + 1] < arr[child])
{
++child;
}
if (arr[child] < arr[parent])
{
Swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
//孩子大于父亲，就跳出循环
break;
}
}
}
2.2.5 获取堆顶元素
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->arr[0];
}
2.2.6 检测堆是否为空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
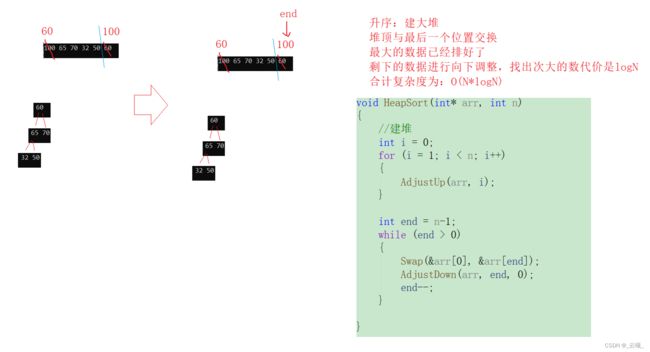
2.3 堆排序
- 堆排序要注意两个点：
- 排升序建大堆
- 排降序建小堆
- 向上调整实现堆排序，时间复杂度：O(N*logN)
- 循环从数组的第二个元素开始向上调整
- 循环从最后一个元素开始往前和堆顶元素交换位置，再向下调整
void HeapSort(int* arr, int n)
{
//向上调整建堆O(N*logN)
int i = 0;
for (i = 1; i < n; i++)
{
AdjustUp(arr, i);
}
int end = n-1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
end--;
}
}
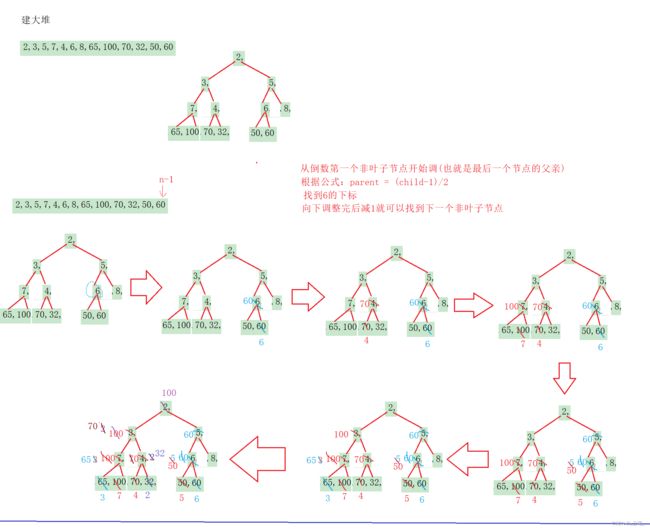
- 向下调整实现堆排序，时间复杂度：O(N)
- 从倒数第一个非叶子节点开始调(也就是最后一个节点的父亲)
- 找到最后一个节点的父亲的方法：
- n-1找到最后一个元素，再按公式parent = (child-1)/2，就可以找到最后一个节点的父亲了，也就是：(n-1-1) / 2
- 向下调整后减1就可以找到下一个非叶子节点的位置，因为物理结构是一个数组，数组存储的元素是连续的
- 循环从最后一个元素开始往前和堆顶元素交换位置，再向下调整
void HeapSort(int* arr, int n)
{
//向下调整建堆O(N)
int i = 0;
for (i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, n, i);
}
int end = n-1;
while (end > 0)
{
Swap(&arr[0], &arr[end]);
AdjustDown(arr, end, 0);
end--;
}
}
2.4 TOPK问题
- 时间复杂度：O(N*logK)
- 空间复杂度：O(K)
- 首先要制造一些数据到文件里
void CreateNDate()
{
// 造数据
int n = 10000;
srand((unsigned int)time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (int i = 0; i < n; ++i)
{
int x = (rand() + i) % 10000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}
int main()
{
//CreateNDate();
//传入文件名和要k的数值
PrintTopK("data.txt", 10);
return 0;
}
- 打开文件，把前k个数据输入到堆里，然后向下调整建堆
void PrintTopK(const char* filename, int k)
{
FILE* pf = fopen(filename, "r");
if (pf == NULL)
{
perror("fopen fail");
exit(-1);
}
int* heap = (int*)malloc(sizeof(int) * k);
if (heap == NULL)
{
perror("malloc fail");
exit(-1);
}
// 1、取出前k个数据建堆
int i = 0;
for (i = 0; i < k; i++)
{
fscanf(pf, "%d", &heap[i]);
}
//2.、前k个数向下调整，建堆
//k-1找到最后一个元素的下标
//(k-1-1)/2找到最后一个节点的父亲节点
for (i=(k-1-1)/2; i>=0; i--)
{
AdjustDown(heap, k, i);
}
fclose(pf);
free(heap);
pf = NULL;
heap = NULL;
}
- 读取剩下的数据，与堆顶比较，大于堆顶就替换进堆，然后再向下调整，建堆
void PrintTopK(const char* filename, int k)
{
FILE* pf = fopen(filename, "r");
if (pf == NULL)
{
perror("fopen fail");
exit(-1);
}
int* heap = (int*)malloc(sizeof(int) * k);
if (heap == NULL)
{
perror("malloc fail");
exit(-1);
}
// 1、取出前k个数据建堆
int i = 0;
for (i = 0; i < k; i++)
{
fscanf(pf, "%d", &heap[i]);
}
//2.、前k个数向下调整，建堆
for (i=(k-1-1)/2; i>=0; i--)
{
AdjustDown(heap, k, i);
}
// 读取剩下的数据依次跟堆顶数据比较，
//大于堆顶就替换进堆，然后再向下调整
int x = 0;
while (fscanf(pf, "%d", &x) != EOF)
{
//大于堆顶就替换它进堆
if (x > heap[0])
{
heap[0] = x;
//替换后，再向下调整
AdjustDown(heap, k, 0);
}
}
for (i = 0; i < k; i++)
{
printf("%d ", heap[i]);
}
printf("\n");
fclose(pf);
free(heap);
pf = NULL;
heap = NULL;
}
- 测试
- 这里有一个调试小技巧，我们写入文件的是随机数，不知道是不是最大的前k个，那么我们就自己在随机位置加入k个大的数值，如果输出出来的是我们自己改的数值，那么程序就是正确的
- 从99991 - 999910都是我自己更改的测试数值
- 测试结果：
2.5本篇章的代码
堆的实现代码