地震勘探基础（五）之地震资料数字处理
地震资料数字处理
地震勘探主要包括地震资料野外采集，地震资料数字处理和地震资料地质解释三大部分。其中地震资料数字处理需要利用高性能的超级计算机和先进的处理软件系统。地震资料的质量和成像精度直接决定了油、气勘探的成功率。
地震资料数字处理的主要目的是提高信噪比，提高分辨率和提高保真度，进而获得更多更精确的地下地质信息。
地震野外采集的数据是以炮集的形式记录，共炮点的地震记录很不直观，与地下地质构造形态关系不明显，不能方便反应地质构造形态和特征，更不能反映岩性储层等方面的变化。
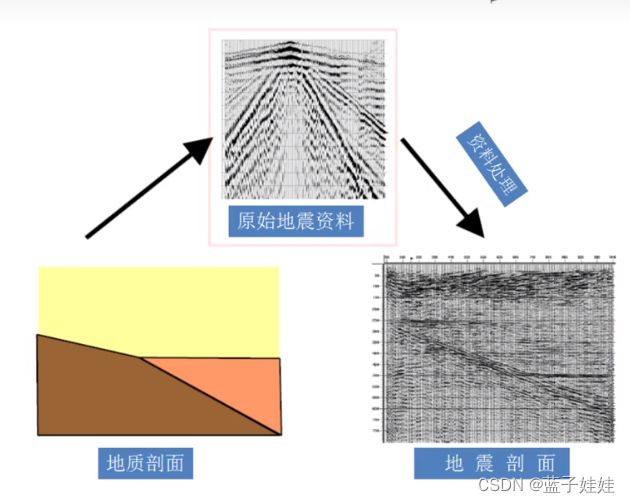
在炮集记录上，除了一次反射波以外，一般还记录了面波，声波，多次反射波和折射波等多种干扰波。需要利用不同的处理方法来进行有效的压制。
地震资料处理流程
如下图所示，地震资料处理流程分为三大步：预处理，叠前处理和叠后处理。
野外采集的地震资料，首先要进行地震常规处理。它主要流程如下：
1）预处理：将野外地震记录的格式转化为计算机能够识别的格式；
2）水平叠加处理：对多次观测的每一个地震道，按反射点的位置叠加成一道；主要包括抽CMP道集，速度分析，动校正和共中心点叠加处理等。
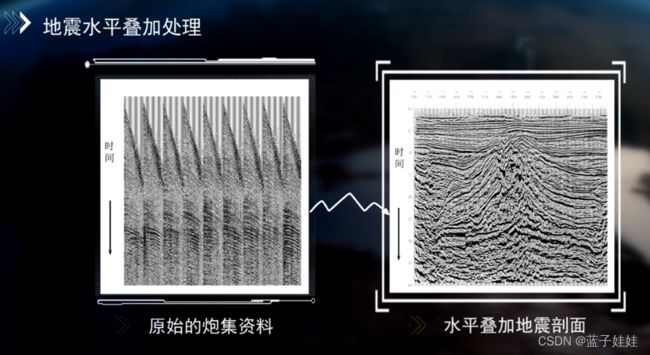
3）叠加偏移处理：纠正由于地层倾角或异常波对水平叠加剖面造成的偏差，以反映地下地层的真实形态。
地震预处理
地震预处理主要包括数据加载，数据解编，观测系统定义，数据编辑和振幅补偿等工作。
数据加载和转换是预处理的第一步，要把野外采集的数据加载到地震资料处理系统中。野外磁带记录数据是按时序排列的，也就是依次地下每一道的第一个采样值各道记完以后，再依次记下各道的第二个采样值，以此类推。
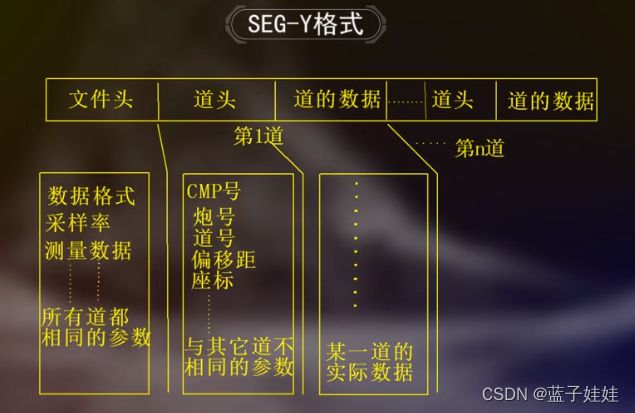
在数据处理中，将时序排列的形式转换为按道序排列，也就是第一道的所有数据都排列在第二道之前，使得同一道数据排列在一起，这种处理称为数据解编或者重排。
野外地震记录一般使用SEG-D或SEG-2的格式，解编后的按道分时的格式为SEG-Y。
观测系统定义也是预处理的重要内容。要确定激发点和接收点坐标以及高程等数据。在观测系统定义中，还需要抽道集，即把具有相同共中心点的炮点对抽出组成共中点点道集。由于施工管理，激发接收，环境因素等影响会产生废炮废道，在进行其它处理之前需要将它们去除。
切除处理是一种充零的处理，它将地震道上某个时刻以前的所有数据用0值替代，在显示上造成一种某个时刻以前的波动能量被切除掉的视觉效果。
影响地震反射波振幅的主要因素包括：
(1) 地质因素；
(2) 波的传播机理：波前扩散和吸收衰减；
(3) 地震激发与接收；
(4) 干扰波等非地质因素。
数字滤波处理
野外地震记录上仍然残留一些干扰波，需要使用室内的方法加以压制。
下图展示了有效波和干扰波的差异
下图展示了有效波与干扰波在频谱上的差异。
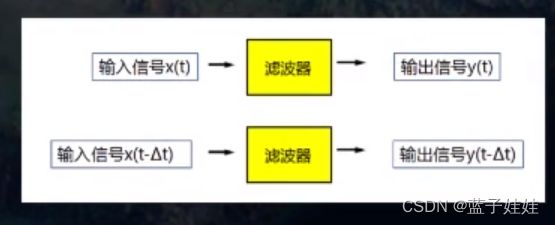
在地震常规处理流程中，数字滤波处理是最常用的方法，比如一维频率滤波，二维频率波数域滤波等。任何一种对输入信号的改造作用都可以看作滤波，实现这种滤波的系统称为滤波器。滤波器可以分为模拟滤波器和数字滤波器。
模拟滤波器也称电滤波器，它由电阻，电感和电容等元件组成。使用数学运算方式通过数字计算机技术对离散信号进行滤波处理的系统称为数字滤波器。它比模拟滤波器更灵活、多样和精确。
根据对输入信号的改造作用，数字滤波器可以分为线性和非线性滤波器。线性滤波器的输出信号只包含输入信号所拥有的成分，不会出现新的成分。非线性滤波器则与之相反，中值滤波就是典型的非线性滤波器。
线性滤波器满足叠加原理和正比定理。
滤波器的时不变性指的是滤波器对输入信号的改造作用与时间无关。现在地震勘探中常用的时线性时不变数字滤波器。
-
滤波器还需要是稳定的，即滤波器的输出能量必须是有限的。模拟滤波器是物理可实现的，满足因果率，在输入以前不能有输出，而数字滤波器则不完全是，比如零相位滤波器则是物理不可实现的。
-
按照滤波器的性质可分为无畸变滤波器，相位畸变滤波器和振幅畸变滤波器。
-
按照滤波器的相位特性可分为最小相位延迟滤波器，混合相位延迟滤波器，最大相位延迟滤波器和零相位滤波器。
-
按照运算维数可分为一维滤波和二维滤波。一维滤波指的是信号或其频谱以及滤波因子等都是单变量函数的滤波。单变量可以是频率或者时间，也可以是波数或者空间。实际工作频率滤波用得最为广泛。二维滤波主要包括时间-空间域，频率-波数域， τ \tau τ- p p p域等。
-
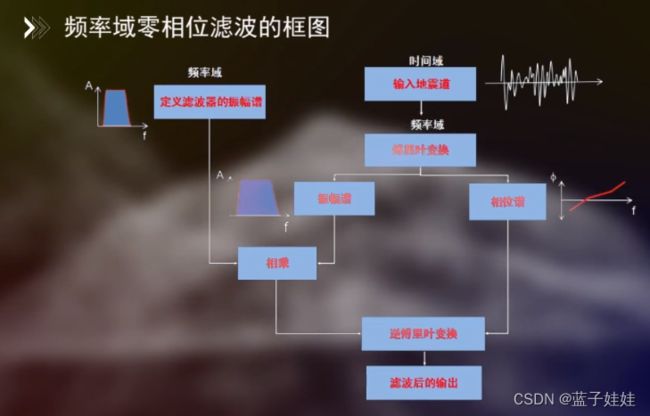
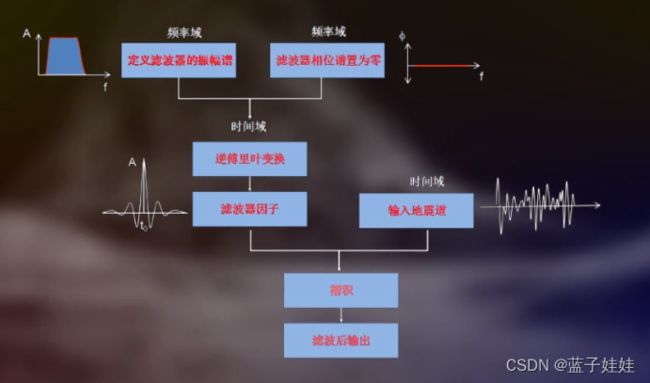
一维频率滤波可以在频率域内进行，地震记录的频谱与滤波器的频谱相乘积，再做傅里叶逆变换即可得到滤波结果。
下图展示了频率域零相位滤波的处理流程。
一维频率滤波也可以在时间域内进行，地震记录和滤波因子的褶积就可以得到滤波结果。可以在频率域中设计好滤波器，然后求取频率滤波器的傅里叶逆变换得到滤波因子。
下图展示了时间域内零相位滤波的处理流程。
四种理想的频率滤波器主要包括低通滤波器，高通滤波器，带通滤波器和陷波滤波器。
低通滤波器允许信号中的低频分量通过，抑制高频干扰，比如可以压制声波干扰。
高通滤波器允许信号中的高频分量通过，抑制低频干扰，可以压制面波干扰。
带通滤波器允许一定频段的信号通过，抑制低或高于该频段的干扰波。
陷波滤波器抑制特定频率的信号，比如可以压制50Hz的高压电干扰。
一维频率滤波可以在共炮点道集，共中心点道集，叠加剖面和偏移剖面上进行。
地震资料实际处理中，需要对地震记录进行频率扫描，确定干扰波的频带范围，进行多次实验后再确定滤波参数。如果干扰波频带范围随时间变化，还需要对地震记录上不同时段采取不同滤波带宽的滤波器，也就是使用时变滤波器进行滤波。
如果有效波和干扰波再频带上重叠，采用一维滤波效果不佳，此时可以采取其它滤波方法如F-K域滤波， τ \tau τ- p p p域滤波，匹配滤波，中值滤波，相干滤波，反假频滤波等等。在多次波压制上，可以采取反褶积，波动方程等方法进行压制。在数字滤波中，还引入了小波变换（wavelet transform）的数学方法。
地震二维数字滤波
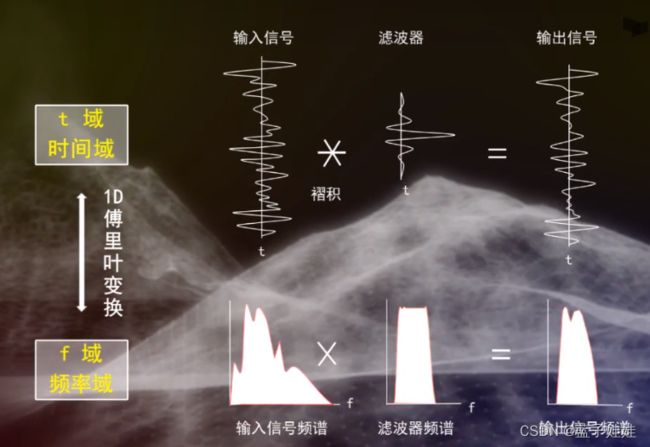
一维频率滤波可以将时间域的地震信号通过一维傅里叶变换到频率域，再把频率域中滤波后的信号通过傅里叶逆变换变换到时间域。
在时间域内进行频率滤波就是地震信号与滤波因子的褶积；在频率域中进行频率滤波就是地震信号的频谱与滤波器频谱的乘积，滤波后再做傅里叶逆变换。
一维频率滤波在地震资料数字处理中发挥了很大的作用，但是有时候有效波和干扰波在频带上是重叠的。
下图是一张共炮点地震记录，存在一些和反射波特征不一样的干扰波，有些干扰波和有效波在频谱上有差异，有的没有差异。
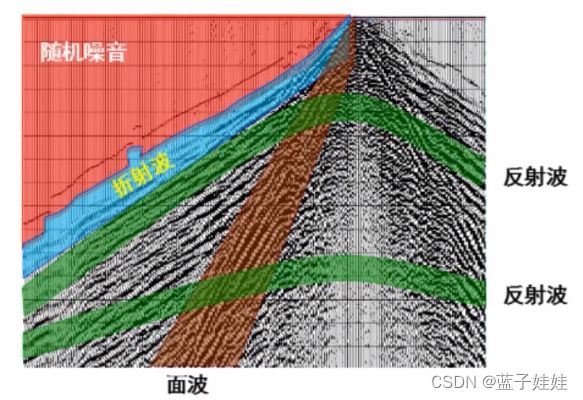
特别是浅层折射波和反射波在频率上的差异很小。因此一维频率滤波不能独立承担起滤掉全部干扰波的重任。
频率-波数域滤波（F-K滤波）或者 τ \tau τ- p p p 滤波等方法可以弥补一维滤波的不足。比如在F-K域中，反射波和一些线性的干扰波具有较大的差异。
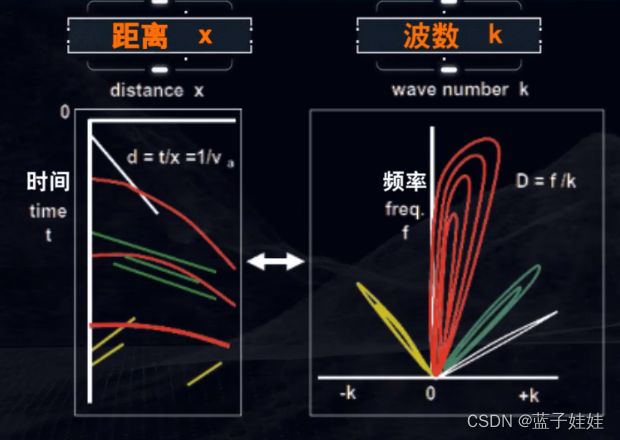
要理解F-K滤波的原理，需要知道几个相关概念。在某一个时刻，质点位移随位置变化的波剖面上，波在一个振动周期内传播的距离称为波长。单位距离内的波长数称为波数，也成为空间频率。
地震波沿着地震测线方向观测的速度和波长称为视速度和视波长，视波数是视波长的倒数。视速度等于频率与视波数之比。视速度和视波长与波的传播方向有关。
利用二维傅里叶变换， t t t- x x x域的共炮点记录变换到F-K域，在F-K域设计滤波器进行滤波后，再进行二维傅里叶逆变换回到 t t t- x x x域，就得到F-K域滤波结果。
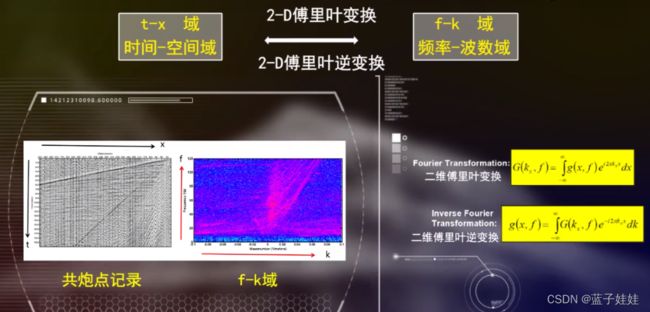
从 t t t- x x x域变换到F-K域，从坐标原点画一条直线，直线的斜率就是视速度 v a v_a va。
在F-K域中，有效波和一些干扰波的分布范围有较大的差异。
地震记录从 t t t- x x x域变换到F-K域后，反射波信号主要集中在频率轴两侧，而面波集中在靠近波数轴附近。高视速度噪音和散射噪音都与反射波信号具有较大的差别。
下图展示了某一共炮点记录的从 t t t- x x x域变换到F-K域后的图谱，可以根据有效波和干扰波的分布特点确定滤波的通放带和切除带。
下图展示了一张实际的中点激发，两侧接收的共炮点地震记录，在F-K滤波后，面波和浅层折射波干扰得到较好的压制。
下图展示了一张单点放炮，一边接收的共炮点地震记录。F-K变换后，在F-K频谱上，反射波主要集中在F轴附近，面波主要集中在K轴附近。
下图展示了野外记录和F-K变换后的频谱图。
在F-K域把干扰波的切除掉后的谱如下图所示，保留了反射波的信息。
下图展示了F-K滤波前后的炮集记录，浅层折射波干扰得到了有效的压制。
下图展示了F-K滤波前后的炮集记录，面波干扰得到了有效的压制。
F-K滤波可以在共炮点道集和共中心点道集进行。另外一种二位滤波方法就是 τ \tau τ- p p p （截距-慢度）滤波。
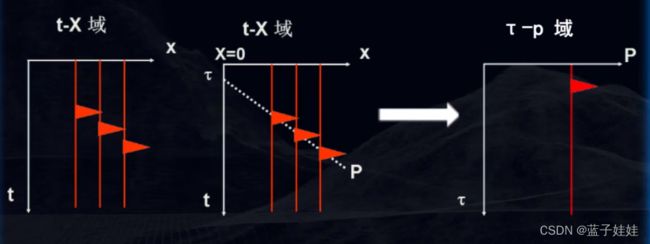
对于t-x域中的共炮点地震记录，利用 τ \tau τ- p p p正变换映射到 τ \tau τ- p p p域，在t-x域中的一系列直线，在 τ \tau τ- p p p域中就是一系列的点。
假定在t-x域中只有一个倾斜的同相轴，这条直线的斜率为P，截距为 τ \tau τ， τ \tau τ- p p p变换之后，在 τ \tau τ- p p p域中这条直线就是一个点。
假设在t-x域，海底反射波是一条双曲线，直达波是一条直线，经过 τ \tau τ- p p p变换后，海底反射波是一条椭圆的曲线，而直达波是一个点。
下图展示了实际的共炮点道集的 τ \tau τ- p p p变换。
假设在t-x域中存在三个反射波同相轴，六个线性干扰。 τ \tau τ- p p p变换后发现，在 τ \tau τ- p p p域中，反射波变成了三个椭圆的同相轴，六个线性干扰变成了六个点，我们可以设计滤波器将这六个点滤掉，再做 τ \tau τ- p p p反变换，就得到不含线性干扰的反射波记录。
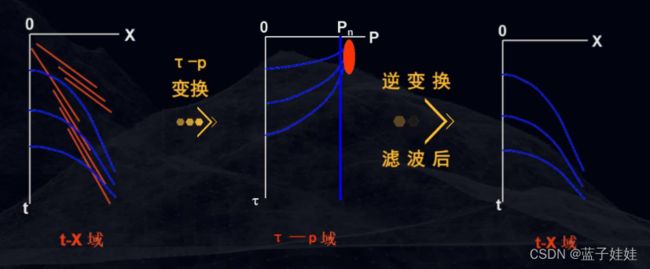
在t-x域中的共炮点地震记录上，存在折射波，直达波和反射波，经过 τ \tau τ- p p p变换后，在 τ \tau τ- p p p域中，折射波就是一个点，在 τ \tau τ- p p p域内可以切除折射波，绿色多边形就是设计的切除范围。
还有一种二维滤波为相干滤波，它是利用相邻地震道有效信号的相干性增强有效信号或者利用相邻地震道噪声的不相干性衰减噪声的一种滤波方法，是一种多道滤波方法。