你还在为 “动态规划” 发愁吗？看完本秘籍，带你斩杀这类题~

目录

前言

一、动态规划——解题思路

二、动态规划——模板以及题目

2.1、Fibonacci

2.2、字符串分割(Word Break)

2.3、三角矩阵(Triangle）

2.4、路径总数(Unique Paths）

2.5、最小路径和(Minimum Path Sum)

2.6、背包问题

2.7、回文串分割(Palindrome Partitioning)

2.8、编辑距离(Edit Distance)

2.9、不同子序列(Distinct Subsequences)

三、总结

---

前言

        前段时间，本人也是之前被动态规划的题目pua过，但是题量上来了以后，理解了你会发现实际上会对应一些模板和套路，需要发挥一点想象力，问题就可以迎刃而解；那么这里呢，就专门针对于一些对类似动态规划的题目无从下手，亦或是怎么想也做不出来的“胖友们”，给你们讲解思路，以及解题方法，希望能够帮到你们！

注意：一定要按文章顺序浏览，并自己动手实践，效果才会显著！

---

一、动态规划——解题思路

        动态规划类的题目本质上来讲，就是需要我们能够大事化小，将大问题分解成一个一个子问题来解决；话不多说，直入正题！

适用场景：

        简单概括就是：最大值/最小值，是否可行，是不是，方案个数；

解题思路：

1.状态的定义（这里就是需要我们针对题目中问到的问题，抽象出子问题；状态定义的是否正确，就要看他是否能对应到最终问题的解）；

2.列出状态转移方程——难点（例如通过一个什么样的公式，可以从第“i-1”这个状态得到第“i”个状态，有时还需要我们去用一个数组保存这个状态）；

3.状态初始化（可以让转移方程继续递推下去）；

4.返回结果；

这样讲还是比较笼统，具体的，我会在下方给出栗子（由浅入深），再进行讲解~

---

二、动态规划——模板以及题目

2.1、Fibonacci

题目描述：

大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。

 题目来源：斐波那契数列_牛客题霸_牛客网

解题思路：

        提示：这道题可以用递归来做，但是不适合，因为一旦数字n过大，时间复杂度就是一个指数级别的O(2^N)，所以这里我们可以考虑用动态规划来实现~

1.状态F(i)：第i项的一个值；(子问题)

2.状态转移方程：F(i) = F(i - 1) + F(i - 2);

        这个方程是怎么得来的呢？前面我们提到说，将大问题化成一个一个相同的子问题，这里的F(i)便是子问题（第i项的一个值），那么思考一下这个值该怎么得来呢？由斐波那契数列的性质我们可以知道，第i项的值，是可以通过第i - 1项的值加上第i - 2项的值得来，因此这个式子就不难理解啦！

3.初始状态：F(0) = 0; F(1) = 1;

        怎么得出的初始状态？这里就需要看状态转移方程，需要几个初始值，才可以得出F(i)，使得这个递推公式可以不断的运转下去；

4.返回结果：F(n) 表示最终问题的解；

具体代码和注释：

public class Solution {
    public int Fibonacci(int n) {
        //定义一个数组，用来保存中间状态
        int[] dp = new int[n + 1];
        //初始化，保证顺利递推
        dp[0] = 0;
        dp[1] = 1;
        //由初始化可以得出第三项，因此i从下标2开始，通过递推公式得到第n项
        for(int i = 2; i <= n; i++) {
            //列出状态转移方程
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        //返回结果
        return dp[n];
    }
}

优化：

        这里，空间上是可以优化的，为什么呢？我们得出第i项的值，实际上只需要前两项的值，即可，再往前面的值就用不上了，也没必要去创建一个数组去保存中间状态；

        因此我们可以通过两个变量来进行递推，并且动态的更新这两个变量即可；

public class Solution {
    public int Fibonacci(int n) {
        if(n == 0 || n == 1) {
            return n;
        }
        int fn = 0;
        int f1 = 1;//这里就是f(n-1)
        int f2 = 0;//这里就是f(n-2)
        for(int i = 2; i <= n; i++) {
            fn = f1 + f2;
            //更新状态
            f2 = f1;
            f1 = fn; 
        }
        return fn;
    }
}

2.2、字符串分割(Word Break)

题目描述：

给定一个字符串s和一组单词dict，判断s是否可以用空格分割成一个单词序列，使得单词序列中所有的单词都是dict中的单词（序列可以包含一个或多个单词）。

例如:

s = "leetcode", dict = ["leet", "code"]

返回true，因为"leetcode"可以被分割成"leet code".

题目来源：拆分词句_牛客题霸_牛客网

解题思路：

1.状态F(i)：字符串的前i个字符是否可以被分割；

        怎么理解呢？首先来看问题：字符串整体是否可以被分割？那么我们可以从整体转换成局部，就是某个子串是否可以被分割，剩下未被分割的部分在字典中是否能够找到，这样一个子问题；（状态定义的是否正确，要看你定义的这个状态或多个这样的状态，最终能否对应上问题的某一个解）

2.状态转移方程：j < i && F(j) && [j + 1, i]是否能在词典中找到；

        解释：我们可以先列出几个栗子，比如字符串"leetcode"，F(4)表示什么？他表示字符串的前4个字符可以被分割，那么如果他为true（这里显然为true），我们就需要关心的是[5,8]这个区间的字符串能否在字典中找到；回到题目中的示例我们的最终问题是，前8个字符能否被分割？那么以此类推，F(8)子问题（F(8)可以由那些状态得出结果?）就变成了如下状态：

• F(1) && [2, 8]是否能在词典中找到；
• F(2) && [3, 8]是否能在词典中找到；
• F(3) && [4, 8]是否能在词典中找到；
• F(4) && [5, 8]是否能在词典中找到；
• F(5) && [6, 8]是否能在词典中找到；
• F(6) && [7, 8]是否能在词典中找到；
• F(7) && [8, 8]是否能在词典中找到；(这里的[8, 8]就是最终的结果)
• F(0) && [1, 8]；这里F(0)表示空字符串（并不表示实际状态），表示整体；
• 这里不能出现F(8)，因为他不能根据自身去推导自身

所以这里状态方程，F(8) = F(j) + F(j + 1, 8);  这里的8就是i，是其中的一个状态（注意根据上面推到，j 是小于 i 的）！

3.初始状态：F(0) = true；

        空串为什么被定义成在字典中找得到呢？因为这里不是说空串就能被找到，而是F(0)没有实际意义，只是一个辅助的状态！ 我们可以想象一下，如果i = 4，也就是我们需要判断F(0) && [1, 4]能否在字典中找到？显然[1, 4]是可以找到的，所以这里的F(0)因该是个true才合理；

4.返回结果：F(字符串的长度) ；

代码如下：

import java.util.*;
public class Solution {
    public boolean wordBreak(String s, Set dict) {
        //定义一个数组，用来表示每个i的状态
        boolean[] dp = new boolean[s.length() + 1];
        //初始化
        dp[0] = true;
        for(int i = 1; i <= s.length(); i++) {
            for(int j = 0; j < i; j++) {
                //表示在前j个字符可以拆分的前提下，j + 1 ~ i个字符可以在字典中找到
                if(dp[j] && dict.contains(s.substring(j, i))) {
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[s.length()];
    }
}

2.3、三角矩阵(Triangle）

题目描述

给定一个三角形 triangle ，找出自顶向下的最小路径和。

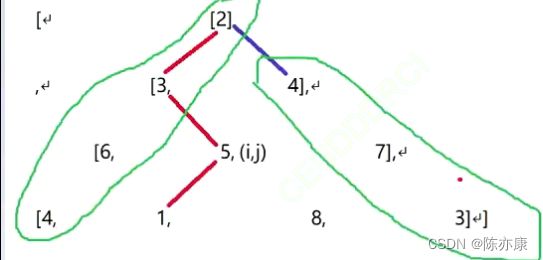
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。如下:

[

[2],

[3,4],

[6,5,7],

[4,1,8,3]

]

题目链接：剑指 Offer II 100. 三角形中最小路径之和 - 力扣（LeetCode）

解题思路一：（自顶而下，不是最优解）

1.状态F(i, j)：从[0,0]出发，到[i, j]点的最小路径和

2.状态转移方程：(0 < j < i)

        当j == 0的时候（最左边的边界）：F(i, j) = F(i - 1, 0) + array[i][j];

        当j == i的时候（最右边的边界）：F(i, j) = F(i - 1, j - 1) + array[i][j];

        剩余的其他情况：F(i, j) = min(F(i - 1, j - 1), F(i - 1, j)) + array[i][j];

        解释：中间某一结点[i, j]的最短路径，就是上一节点（正上方，或左上方的最小值路径和） 加上当前结点的路径和(array[i][j]);

        注意：边上的点都只有唯一一条路径可以到达(j == 0 || j == i)，如下图

3.初始状态：F(0, 0) = array[0][0];

        解释：[0, 0]这个点无法在从上一个点的来，也就是一个固定值；

4.返回结果：min(F(最后一行))；

        解释：这里便是要返回最后一行的最小值；

代码如下：

class Solution {
    // [2],
    // [3,4],
    // [6,5,7],
    // [4,1,8,3]
    public int minimumTotal(List> triangle) {
        int row = triangle.size();//行
        //这里是否创建新的数组？可以不用创建的，题目中所给数组以及满足需求，我们
        //可以直接根据题目中所给的数据继续递推下去
        for(int i = 1; i < row; i++) {
            for(int j = 0; j <= i; j++) {
                if(j == 0) {//左边边界：只能有上面的一个元素得出
                    triangle.get(i).set(j, triangle.get(i - 1).get(j) + triangle.get(i).get(j));
                } else if(i == j) {//右边边界：只能由左上方的元素得出
                    triangle.get(i).set(j, triangle.get(i - 1).get(j - 1) + triangle.get(i).get(j));
                } else {//其他情况
                    triangle.get(i).set(j, Math.min(
                        triangle.get(i - 1).get(j), triangle.get(i - 1).get(j - 1)
                    ) + triangle.get(i).get(j));
                }
            }
        }
        //返回最底层的最小值
        int min = Integer.MAX_VALUE;
        for(int i = 0; i < row; i++) {
            min = Math.min(min, triangle.get(row - 1).get(i));
        }
        return min;
    }
}

解题思路二：（自底而上 —— 最优解，更简洁）

        解法一介绍的是一个从上往下推到的结果，但是实际上还有更容易的办法，就是从最后一行（最底层）向上推到，推到顶层；来看看怎么做吧！

1.状态F(i, j)：从(i, j)到达最后一行的最短路径（注意这里变化，不是从(0, 0)出发了）；

2.状态转移方程：

        F(i, j) = min(F(i + 1, j), F(i + 1, j + 1)) + array[i][j];

        解释：就是从下方的两条路到达选择最小的一条路径到达(i, j);

        这样定义的好处：不用处理边界条件啦，因为自底向上，每一个解都有两条路径，并且最终的解就是[0, 0]这个点，不用再遍历最底层找出最小值啦！

3.初始状态：就是最后一行值（用题目中所给的数组即可）

4.返回结果：就是[0, 0]点；

代码如下：

class Solution {
    public int minimumTotal(List> triangle) {
        //自底而上
        int row = triangle.size();
        for(int i = row - 2; i >= 0; i--) {//这里最后一行就是初始值，所以要从倒数第二行开始
            for(int j = 0; j <= i; j++) {
                triangle.get(i).set(j, Math.min(
                    triangle.get(i + 1).get(j), triangle.get(i + 1).get(j + 1)
                ) + triangle.get(i).get(j));
            }
        }
        return triangle.get(0).get(0);
    }
}

2.4、路径总数(Unique Paths）

题目描述：

一个机器人在m×n大小的地图的左上角（起点）。

机器人每次可以向下或向右移动。机器人要到达地图的右下角（终点）。

可以有多少种不同的路径从起点走到终点？

题目来源：不同路径的数目(一)_牛客题霸_牛客网

解题思路：

1.状态F(i, j)：从(0, 0)到达(i, j)点的路径个数

2.状态转移方程：

        最顶层或最右侧第一列（i == 0 || j == 0）: F(i, j) = 1;

        其他情况：F(i, j) = F(i - 1, j) + F(i, j + 1)；

        解释：到达(i, j)的路径个数，实际上就是上方结点的路径个数加上左方结点的路径个数之和(这里一定是一个一步的操作，想一想，那些点可以一步到达这个状态)；

3.初始状态：F(0, j) = 1，F(i, 0) = 1;

        解释：这里可以想象一下通过转移方程能够得出的第一个状态是谁呢？也就是(1, 1)这个点，因为这个点就可以从(1, 0)加上(0, 1)得到，那么，这两个点怎么初始化呢？ 因为机器人只有两种路径可以走，一种是向右，一种是向下，想象一下，从(0, 0)出发，是不是对于最顶层，只有一条路径能到达（只能向右走）？是不是对于最左侧的第一列，只有一条路径能到达（只能向下走）？

4.返回结果：F(m - 1, n - 1); 最右下方星星表示的格子；

代码如下：

import java.util.*;
public class Solution {
    public int uniquePaths (int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(i == 0 || j == 0) {//最左侧和最上层
                    dp[i][j] = 1;
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

2.5、最小路径和(Minimum Path Sum)

题目描述：

给定一个由非负整数填充的m x n的二维数组，现在要从二维数组的左上角走到右下角，请找出路径上的所有数字之和最小的路径。
注意：你每次只能向下或向右移动。

题目来源：带权值的最小路径和_牛客题霸_牛客网

解题思路：

        与路径总数那道题类似，只是这里的每个格子赋值了，并求最小和；

1.状态F(i, j)：从(0, 0)点到(i, j)的最小路径和；

2.状态转移方程：

        第一层(i == 0 && j > 0)：F(0, j) = F(0, j - 1) + array[0][j];

        第一列(j == 0 && i > 0)：F(i, 0) = F(i - 1, 0) + array[i][0];

        其他(i > 0 && j > 0)：F(i, j) = min(F(i - 1, j), F(i, j - 1)) + array[i][j];

        解释：这里实际上和“路径总数” ，“三角矩阵”题目类似，每个格子被赋值了，并且是求不同路径能达到的最小和，方法是一样滴！

3.初始状态：F(0, 0) = array[0][0];

4.返回结果：F(m - 1, n - 1); 最右下方星星表示的格子；

代码如下：

import java.util.*;
public class Solution {
    public int minPathSum (int[][] grid) {
        int row = grid.length;
        for(int i = 0; i < row; i++) {
            for(int j = 0; j < grid[i].length; j++) {
                if(i == 0 && j > 0) {//第一层
                    grid[i][j] = grid[i][j - 1] + grid[i][j];
                } else if(j == 0 && i > 0) {//第一列
                    grid[i][j] = grid[i - 1][j] + grid[i][j];
                } else if(i > 0 && j > 0){
                    grid[i][j] = Math.min(
                        grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
                }
            }
        }
        return grid[row - 1][grid[row - 1].length - 1];
    }
}

2.6、背包问题

题目描述：

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值.

问最多能装入背包的总价值是多大?

题目来源：125 · 背包问题（二） - LintCode

解题思路（不是最优解，二维数组）：

        分析：这里有很多种情况，比如拿到的物品可能是：（体积大，价值大）、(体积大，价值小)......那么这里，需要考虑的因素就不止一种了，即需要考虑价值，还需要考虑体积（例如：包装不下，需要从包取出几个元素，再放入，又或是直接抛弃...）所以这里定义状态时，一维数组时满足不了的，这里需要一个二维数组；

1.状态F(i, j)：（重点理解这里的状态，否在后面看不懂！）从前i个商品中选择，包的大小为j（j是包的总大小）时，所能放下的最大价值；

2.状态转移方程：

        第i个商品可以放入（虽然可以，但是不一定放入）大小为j的包中：

•         A(i - 1) <= j && F(i, j) = max(F(i - 1, j), F(i - 1, j - A[i - 1]) + V[i - 1]);

        第i个商品不可以放入大小为j的包中（商品本身以及超出包的大小，怎么都放不进去）：

•         A(i - 1) > j && F(i, j) = F(i - 1, j);

        解释：

        F(i - 1, j - A[i - 1]) + V[i - 1])中的“j - A[i - 1]”表示为第i个商品预留出来的空间，也就是说（这里请重点理解！！！）第i个商品先不放入！只是预留出来的空间！因为这里通过从前i - 1个商品中做选择，在大小为j - A[i - 1]的包中已经选择出了存放最大价值的商品的方案，最后，由于已经预留好了空间，直接加上第i个商品的价值即可！！！

        对F(i - 1, j - A[i - 1]) + V(i - 1)) 整体的解释：两种情况，一是放入第i个商品 ---> F(i - 1, j - A[i - 1]) + V[i - 1]) ---> F(i, j)表示了 “不够放入第i个商品，需要从背包中取出某些商品，再放入” 和 “包的大小足够，直接放入第i个商品” ；二是不放入第i个商品 ---> F(i - 1, j) ---> F(i, j)；通过这两种情况比较最大值可以决定是否把第i个商品放入；

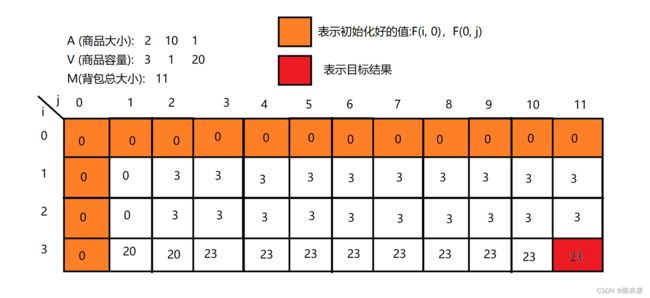
        举个栗子：如下图

        这里如果选择放入第二个商品，则F(i - 1, j - A[i - 1]) + V(i - 1)) = F(2 - 1, 11 - 10) + 1 = F(1,1) + 1; 那么这里的F(1, 1)实际上就是一个空包，因为从前i个商品中做选择，放入大小为1的包中，但是第一个商品的大小为3，显然放不下，所以这里就表示放入第二个商品后最大价值为1；这合理吗？显然不合理，因为要去比较如果不放入第i个商品的价格F(1, 11) = 3 ，看第二个商品是否值得被放入，所有就有了F(i, j) = max(F(i - 1, j), F(i - 1, j - A[i - 1]) + V(i - 1));

3.初始化：F(i, 0) = 0, F(0, j) = 0;

4.返回结果：F(n, m);

还不情况，可以看看这个栗子：（如下图）

 代码如下：

public class Solution {
    public int backPackII(int m, int[] a, int[] v) {
        int n = a.length;//表示商品总个数
        int[][] dp = new int[n + 1][m + 1];
        //初始化(默认是0，就不用了)
        // for(int i = 0; i <= m; i++) {
        //     dp[0][i] = 0;
        // }
        // for(int i = 0; i <= n; i++) {
        //     dp[i][0] = 0;
        // }
        //递推
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(a[i - 1] <= j) {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - a[i - 1]] + v[i - 1]);
                }else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n][m];
    }
}

优化（最优解，一维数组）：

        分析：上面解法是将其抽象成了二维数组的形式，实际上，一个一维数组就可以搞定，因为每次更新元素的时候，只需要用到上一行当前列的值和上一行某一列的值，所以可以将当前行未更新的值作为上一行的值， 并且要注意，更新值的时候需要倒序更新（原因就是上句话），这样空间上就得到了一个优化；

代码如下：

public class Solution {
    public int backPackII(int m, int[] a, int[] v) {
        int n = a.length;//表示商品总个数
        int[] dp = new int[m + 1];
        //递推
        for(int i = 1; i <= n; i++) {
            //注意这里要从后向前打印，因为这一行未更新的值就是上一行的值，而我们需要的就是
            //上一行当前列和上一行前面某一列的值；
            for(int j = m; j > 0; j--) {
                if(a[i - 1] <= j) {
                    dp[j] = Math.max(dp[j], dp[j - a[i - 1]] + v[i - 1]);
                }
                //else的部分也就不需要了，因为从后往前更新，未更新的值就是上一行的值
                //也就是说，当a[i - 1]>j时，直接不用管就可以了；
                // else { 
                //     dp[i][j] = dp[i - 1][j];
                // }
            }
        }
        return dp[m];
    }
}

---

2.7、回文串分割(Palindrome Partitioning)

题目描述：

给出一个字符串s，分割s使得分割出的每一个子串都是回文串

计算将字符串s分割成回文分割结果的最小切割数

例如:给定字符串s="aab",

返回1，因为回文分割结果["aa","b"]是切割一次生成的。

题目来源：132. 分割回文串 II - 力扣（LeetCode）

解题思路：（不是最优解，以下解法时间复杂度为O(n^3)）

1.状态F(i)：s的前i个字符最小的分割次数

2.状态转移方程：

        若整体是回文串[1, i]，则F(i) = 0;

        j < i && [j + 1, i]是回文串，则F(i) = min(F(j) + 1); （这里是遍历找出最小值）;

        解释：怎么的出来这个方程呢？动态转移方程，就是需要通过中间的某一状态，来一步推出下一个状态； 

        第一步)、假设我们以"baa"为例，假设我们需要求出F(3)，那么可以想想，可以利用他的前一个状态F(2)吗？F(2)就表示前俩个字符的最小分割次数，那么，想推出F(3)就需要保证F(2)到F(3)中多出来的字符串"a"必须是回文的(若不回文，就不用管，直接跳过)，这样就可以通过在F(2)计算的结果上加1得出F(3)，而F(2) ---> b|a 到 F(3) ---> b|aa 无非就是多了一个字符"a"，这一个字符必然是回文的，所以根据以上方法就可以得出F(3) = F(2) + 1 = 1 + 1 = 2；

        第二步)、再想一想，光看F(2)这一个状态够吗？显然不够，因此我们可以再看看F(1)是否可用，F(1)就表示前1个字符的最小分割次数，根据上面所讲到的方法，我们只需要确保F(1) 到F(3)中多出来的字符"aa"是回文的，那么就可以通过F(1) + 1的方法推出F(3)，显然，"aa"是回文的，那么F(3) = F(1) + 1 = 0 + 1 = 1；这里算出的F(3)要小于 第一步 中算出的F(3)，根据题目要求，所以我们取这里的F(3)；

        第三步)、综上，想要得出第i个状态的值，我们需要将[1, i]这个区间都遍历一遍，并用上述方法选举出一个最小值即可；

3.初始状态：F(i) = i - 1;

        解释：每一个字符串的最大分割次数都是字符串的长度-1次，也就是分成一个个单字符，这样写就方便了转移方程比较最小值

4.返回结果：F(s.length())；

代码如下：

class Solution {
    public int minCut(String s) {
        int len = s.length();
        if(len == 0) {
            return 0;
        }
        if(judge(s, 0, len - 1)) {
            return 0;
        }
        int[] dp = new int[len + 1];
        //初始化
        //填充可以被分割的最大次数
        for(int i = 1; i <= len; i++) {
            dp[i] = i - 1;
        }
        for(int i = 2; i <= len; i++) {
            if(judge(s, 0, i - 1)){//若前i个字符串整体回文
                dp[i] = 0;
                continue;
            }
            for(int j = 1; j < i; j++) {
                if(judge(s, j, i - 1)) {//注意索引
                    dp[i] = Math.min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[len];
    }
    //判断回文
    private boolean judge(String s, int start, int end) {
        while(start < end) {
            if(s.charAt(start) == s.charAt(end)) {
                start++;
                end--;
            } else {
                break;
            }
        }
        return start < end ? false : true;
    }
}

优化：（最优解，时间复杂度为O(n^2)）

        解释：想要在时间复杂度上得到优化，就需要用空间来换取时间；实际上，判断回文串这里也可以用动态规划来解，并用一个二维数组保存每一种状态是否回文；

1.状态F(i, j)：[i, j]这个子区间为回文串；

2.状态转移方程F(i, j)：

        若i + 1 == j  则 F(i, j) : s[i] == s[j];

        其他情况 F(i + 1, j - 1) && s[i] == s[j]; 

解释： 

        若区间[i + 1, j - 1]是一个回文串，那么只需要保证字符串的第 i 个字符和字符串的第 j 个字符相等，就可以推出[i, j]这个i区间是回文；

注意：根据方程写法，由于需要用到上一行的结果，所以需要从最后一行开始更新；由于是判断回文，所以只需要更新一半即可；

3.初始化：i == j ，则F(i, j) = true;

4.返回结果：F(0, s.length() - 1);

代码如下：

class Solution {
    //获取回文信息
    private boolean[][] getMat(String s) {
        int n = s.length();
        boolean[][] dp = new boolean[n][n];
        for(int i = n - 1; i >= 0; i--) {
            for(int j = i; j < n; j++) {
                if(i == j) {
                    dp[i][j] = true;
                } else if(i + 1 == j) {
                    dp[i][j] = s.charAt(i) == s.charAt(j);
                } else {
                    dp[i][j] = (dp[i + 1][j - 1]) && (s.charAt(i) == s.charAt(j)); 
                } 
            }
        }
        return dp;
    }

    public int minCut(String s) {
        int len = s.length();
        if(len == 0) {
            return 0;
        }
        if(judge(s, 0, len - 1)) {
            return 0;
        }
        int[] dp = new int[len + 1];
        //初始化
        //填充可以被分割的最大次数
        for(int i = 1; i <= len; i++) {
            dp[i] = i - 1;
        }
        boolean[][] mat = getMat(s);
        for(int i = 2; i <= len; i++) {
            if(judge(s, 0, i - 1)){//若前i个字符串整体回文
                dp[i] = 0;
                continue;
            }
            for(int j = 1; j < i; j++) {
                if(mat[j][i - 1]) {//注意索引
                    dp[i] = Math.min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[len];
    }    
    //判断回文
    private boolean judge(String s, int start, int end) {
        while(start < end) {
            if(s.charAt(start) == s.charAt(end)) {
                start++;
                end--;
            } else {
                break;
            }
        }
        return start < end ? false : true;
    }
}

2.8、编辑距离(Edit Distance)

题目描述：

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

题目来源：72. 编辑距离 - 力扣（LeetCode）

解题思路：

1.状态F(i, j)：word1前i个字符到word2的前j个字符的编辑距离；

2.状态转移方程：

        F(i, j) = min(插入，删除，替换) = min(F(i, j - 1) + 1, F(i - 1, j) + 1, F(i - 1, j - 1) + (w1[i] == w2 ? 0 : 1))

        解释：状态转移一定是一个一步的操作，所以想要得到F(i, j)，我们可以往前推，如下，

        F(i, j - 1)：表示 w1 的前 i 个字符已经变成了 w2 中的前 j - 1 个字符，所以只需要在此基础上插入一个字符，就可以变换到 F(i, j)；

        F(i - 1, j)：表示 w1 的前 i - 1 个字符已经变成了 w2 中的前 j 个字符，所以只需要在此基础上删掉一个字符，就可以变换到 F(i, j);

        F(i - 1, j - 1)：表示 w1 的前 i - 1 个字符已经变成了 w2 中的前 j - 1 个字符，所以只需要在此基础上 先判断第i个字符与第j个字符是否相等，若相等就直接是 F(i, j)，若不相等，就需要替换一个字符，才能变换到F(i, j)；

        例如：w1 = "bi"，w2 = "ke"；（具体表格如下图）

3、4.初始化和返回结果都在上图中体现；

代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int row = word1.length();
        int col = word2.length();
        int[][] min = new int[row + 1][col + 1];
        //初始化
        for(int i = 0; i <= row; i++) {
            min[i][0] = i;
        }
        for(int i = 1; i <= col; i++) {
            min[0][i] = i;
        }
        //递推
        for(int i = 1; i <= row; i++) {
            for(int j = 1; j <= col; j++) {
                //先求插入和删除中的最小步骤
                min[i][j] = Math.min(min[i][j - 1], min[i - 1][j]) + 1;
                //替换
                if(word1.charAt(i - 1) == word2.charAt(j - 1)) {//相等则不需要替换(不用加1)
                    min[i][j] = Math.min(min[i][j], min[i - 1][j - 1]);
                } else {//不相等
                    min[i][j] = Math.min(min[i][j], min[i - 1][j - 1] + 1);
                }
            }
        } 
        return min[row][col];
    }
}

2.9、不同子序列(Distinct Subsequences)

题目描述：

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

题目数据保证答案符合 32 位带符号整数范围。

题目来源：115. 不同的子序列 - 力扣（LeetCode）

解题思路：（空间复杂度未优化）

问题：S中与T相等的子序列的个数；

1.状态F(i, j)：S的前 i 个子串构成的子串中与T前 j 个字符相同的子序列的个数；

2.状态转移方程：

        if(S[i] == T[i])  F(i, j) = F(i - 1, j - 1) + F(i - 1, j)；

        if(S[i] != T[i])  F(i, j) = F(i - 1, j)；

解释：

        F(i - 1, j - 1)就表示使用第i个字符，并且只能为最后一个字符，相当于和T的第j个字符匹配；F(i - 1, j)就表示不使用第i个字符；这两种情况是完全互斥的；例如T:"rabbb"，S:"rabb"，那么

S[5] == T[4]: 如果使用第五个字符，那么就要向前找看是否还有最后一个字符匹配的;

即F(4, 3) = rab 或 ra b  + S[5]；F(4, 4) = rabb；

3.初始状态：F(i, 0) = 1；j != 0 && F(0, j) = 0;

        解释：F(i, 0)相当于是从前i个字符中找空串，那是可以找到的；j != 0 && F(0, j) = 0相当于从空串中找非空字符串，肯定是找不到的，所以是0；

4.返回结果：F(s.length(), t.length());

代码如下：

class Solution {
    public int numDistinct(String s, String t) {
        int row = s.length();
        int col = t.length();
        int[][] dp = new int[row + 1][col + 1];
        //初始化
        dp[0][0] = 1;
        //递推
        for(int i = 1; i <= row; i++) {
            dp[i][0] = 1; //初始化第一列
            for(int j = 1; j <= col; j++) {
                if(s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];//使用和不使用第i个字符
                } else { //不相等，就退化到上一级
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[row][col];
    }
}

优化：（空间复杂度优化）

        这里类似于之前的背包问题，通过转移方程可以看出，一直只用到的上一行的某一列的值，所以这个时候，我们可以用一个一维数组来代替，未被更新的值上一行的值，更新后的值就是当前行，所以这个时候也要注意同样的问题：每一行后需要从后向前更新~

class Solution {
    public int numDistinct(String s, String t) {
        int row = s.length();
        int col = t.length();
        int[] dp = new int[col + 1];
        //初始化
        dp[0] = 1;
        //递推
        for(int i = 1; i <= row; i++) {
            for(int j = col; j > 0; j--) {
                if(s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[j] = dp[j - 1] + dp[j];//使用和不使用第i个字符
                }
            }
        }
        return dp[col];
    }
}

---

三、总结

做完这些题，在回头看看开头的总结的东西，是不是感觉都会很不一样！

这里再做一个小的总结：

        状态来源：从问题中抽象状态；

        抽象状态：每一个状态对应一个子问题；

        状态定义（难点）有很多，如何验证状态的合理性：1.某个状态的解或者多个状态的解能否对应到最终问题的解；2.状态之间可以形成递推关系；

        定义一维状态还是二维状态？优先一维，当其不满足合理性时，再选择二维；

常见问题定义原则

        字符串问题：状态一般对应子串，状态中的递推一般会增加一个新的字符；

        矩阵：往往对应二维状态，通过优化可以使其转变为一维；

---

码字不易~

很肝~