实现map和set
map和set的底层就是红黑树,所以只要实现了红黑树,就可以考虑封装出map和set。所以本文会重点介绍我是如何一步步封装map和set,就不会再介绍红黑树的实现,实现可看我上篇博客,个人觉得封装中最麻烦的就是模板参数和迭代器,所以本文从这两个方面入手。红黑树博客链接在下:
红黑树的部分功能实现_小何只露尖尖角的博客-CSDN博客
第一 模板参数
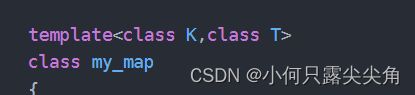
map和set都是模板,使用时都要先显示实例化 , set只要传一个类型实例化K即可,因为set中只存一个关键码-key , 而map要给K , T实例化成具体的类型(K,T分别对应map K-V结构的关键码-key和存的数据-value) , 那为什么map的模板参数不命名为K,V呢?这其实牵扯到一个问题,那就是树中存的是什么?(红黑树模板参数会提及)
map和set的底层就是红黑树,那是如何将红黑树的函数给map和set呢, 可以用继承,或者是组合。至于为什么此时用组合呢?我觉得在map和set内部定义了一个红黑树变量(这种方式称为组合),比继承的耦合度更低,或许可以减少后期维护的工作量。而这个红黑树也是一个模板,所以定义该变量也要传模板参数。如下
1 从map和set的传参来看
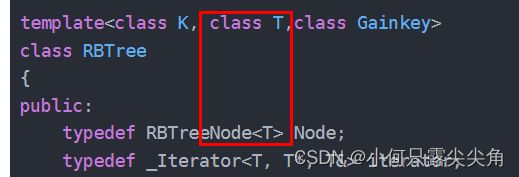
红黑树接收的模板参数如下:
T是节点存的数据类型,K就是关键码key的数据类型,第三个模板参数先不用理会。
当我们大致解释了红黑树的模板参数的意义,也就知道了第一个模板参数是set和map的关键码key的数据类型, 第二个是map和set在节点存的数据类型。
set给红黑树传的模板参数如下:
set(set是把K传给红黑树的模板参数T实例化),set库里把K重命名为value然后传给T(T指的是红黑树模板参数),而map是把一个pair重命名为value传给T,这种重命名为value个人觉得是为了统一记忆 , value是外部传给红黑树节点的数据类型 , 免得一会是K,一会是pair。
为了避免混淆,不让大家以为map模板参数V是value_type的缩写,所以库里的map的模板参数是K和T,而不是K和V,我们为了与库里命名,函数实现保持一致,便于我们理解库里的实现,也用K ,T做map的模板参数。
(set官网文档如下图)
(map官网文档如下图)
map给红黑树传的模板参数如下:
那为什么map传给红黑树的T不是自己模板参数的T呢,而是一个pair呢,如果传的是自己的模板参数T,这样K,T不都传过去了吗?传pair不是浪费吗?
可是你看看下面节点类RBTreeNode
而map是k-v结构的,例如统计字符串出现次数, 那map实例化应该是map
2 红黑树接收模板参数来看
我们先前勉强了解了红黑树模板参数T,map传一个pair类型给T接收 , 而set传的是一个k类型。
我们可以看到的是RBTree的模板参数还有两个。由于insert有可能是插入一个pair,也有可能是插入一个key值,由此却引发另外一个问题 , 那就是insert插入元素是要做大量的判断的,map插入的data是pair类型的,按二叉搜索树规则,要当前根节点cur比较key的值找插入位置,而cur是要用cur->_data.first才能取到key的值,而data则也要用.first访问到key,但是set插入的数据就是key的值,可以直接用cur->_data和插入的data比较,此时难道又要写两份代码吗?当然不是,所以我们就用一个仿函数将pair中的key返回来,而set为了保持一致,也得传个仿函数,只是这个仿函数几乎不做处理,这就是第三个模板参数的作用。
Set仿函数如下:
没有做什么处理就直接返回
Map仿函数如下:
取出key返回,此处是set为了配合map做出的让步,后续我们会在迭代器处看到map和set的其它冲突。在多种冲突下能维持一种特殊的平衡是一件很有成就感的事。
使用场景如下:(在比较处就用这个仿函数)
好好好,那为什么还要传个k呢,不是多余吗 , 那你想想find的参数那个const K& key中的K是哪来的,如果不传K,那find的参数类型如何确定,那个仿函数可取不出来,取得可不是类型,那是数据。
第二 使key不可修改
还有个难啃的骨头,set和map的key可修改的问题,但是只要我们把key可修改和模板参数的问题理清了,封装就过去了。
1 解决set的key
const迭代器是节点数据不能修改, 普通迭代器则可以修改节点数据,但是set中的节点数据只有key关键码,key是不能修改的, 所以set的普通迭代器也不能修改这个关键码,也就是说我们要让set的const迭代器和普通迭代器保持一致。
迭代器iterator本质是my_set类和my_map类内部的一个类型,然后用这个类型来定义变量使用。
My_Structure::my_set::iterator sit = s1.begin();
所以要想取出来的iterator这个类型定义出来的变量,有const_iterator的作用,我们就得对const_iterator进行typedef重命名,将const_iterator命名为iterator,这样就有种偷梁换柱的效果,你以为取出来的iterator是普通迭代器,其实是const_iterator假扮的(如下)。
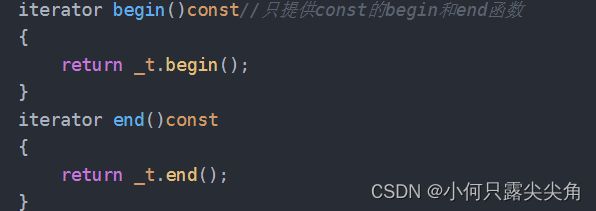
所以set只提供加了const的begin和end函数,这样不管外部的set变量是不是const的,都只会调用这个被const修饰的begin和end函数,也就只会返回const迭代器了。注:此处的iterator是const_iterator重命名的。
2 解决map的key
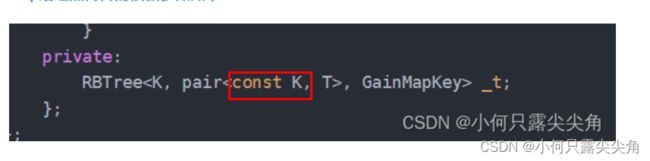
map就不能用set的方法了,因为这样map的pair就是有const属性的了,那first是key不被修改可以,second是有被修改的需求的,一刀切是不行的。大佬的想法总是让人意想不到,那就是直接就把pair中的K传为const K, 这样普通迭代器就只会限制key,而不会限制value。
还有值得一提的是,这种方法为什么不用在set上呢,可能会限制某些功能的开发,所以大佬就没用,但是就我们这点功能还是可以对set用传const key的方法。
我们先记住这两个容器实现const迭代器的方法,由此产生的问题才刚刚开始,下面介绍map和set的成员函数会再说。
第三 map和set的成员函数
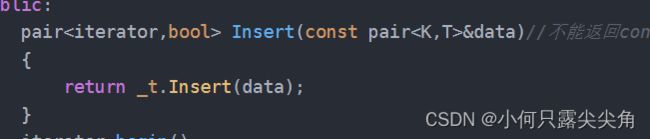
set的insert
_t这个红黑树变量调用自己的insert函数返回的pair
大佬们想了一种办法就是,我们先用匹配类型接收,然后调用构造函数来转换类型(这一步可以在后面完整代码介绍再好好体会),这一步太妙了,我才意识到,构造函数的本质其实是一种类型的转换。
还要解释一点就是typename这个关键字的意思,因为我们要取的红黑树类内的iterator,所以要指定类域,但是这个类没有被实例化,编译器不知道你取出来的是静态变量还是一种类型,因为我们取静态变量也是用类域::这种方式访问,犹豫不决编译器就选择报错了,所以有了typename,告诉编译器你先别报错,我这肯定是类型,等我实例化你再核实。
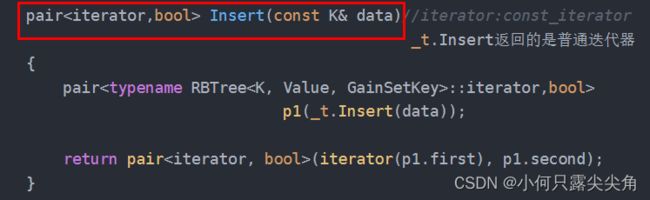
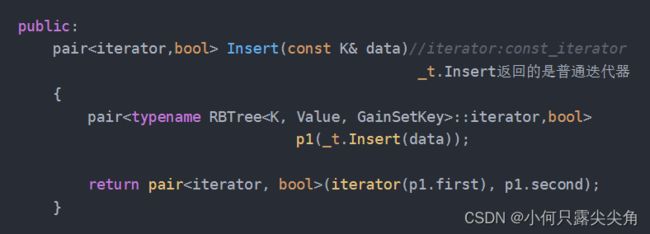
map的insert
类型匹配,不用做处理。
map的[]重载
[]重载的妙用:map
封装set
set的insert,begin,end函数都介绍完了,下面完整的发出封装代码,代码不多。
namespace My_Structure
{
template
class my_set
{
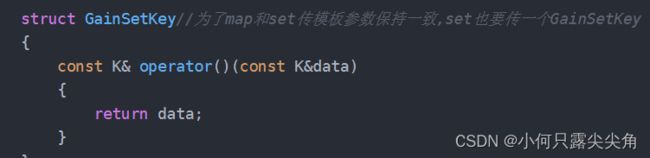
struct GainSetKey 为了map和set传模板参数保持一致,set也要传一个GainSetKey
{
const K& operator()(const K&data)
{
return data;
}
};
public:
typedef typename RBTree::const_iterator iterator;
typedef typename RBTree::const_iterator const_iterator;
public:
pair Insert(const K& data)//iterator:const_iterator
_t.Insert返回的是普通迭代器
{
pair::iterator,bool>
p1(_t.Insert(data));
return pair(iterator(p1.first), p1.second);
}
iterator begin()const//只提供const的begin和end函数
{
return _t.begin();
}
iterator end()const
{
return _t.end();
}
private:
RBTree _t;
第一个模板参数k是给find使用的,第二个是给RBTree节点使用的
};
}; 封装map
如下封装代码,map只剩下begin和end函数没提,其余的都讲过了,map的begin和end函数要提供const和非const的,如果只有const的,那返回就都是带const迭代器的pair了。
namespace My_Structure
{
template
class my_map
{
struct GainMapKey//用来返回pair中的key
{
const K& operator()(const pair& data)
{
return data.first;
}
};
typedef typename RBTree, GainMapKey>::iterator iterator;
typedef typename RBTree, GainMapKey>::const_iterator const_iterator;
public:
pair Insert(const pair&data)//不能返回const迭代器,这样[]无法修改val
{
return _t.Insert(data);
}
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
const_iterator begin()const
{
return _t.begin();
}
const_iterator end()const
{
return _t.end();
}
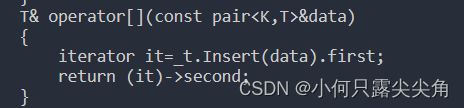
T& operator[](const pair&data)
{
iterator it=_t.Insert(data).first;
return (it)->second;
}
private:
RBTree, GainMapKey> _t;
};
}; 第三 其余完整代码
节点类
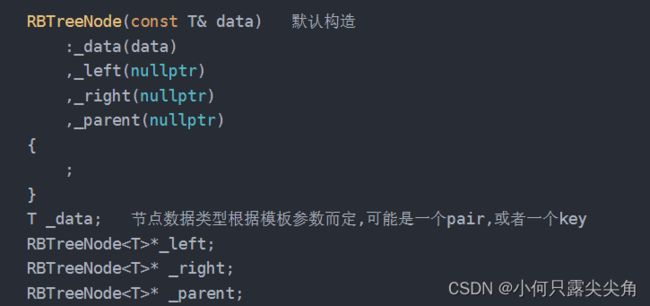
一个模板参数T,使得_data可以是任意类型的数据。
enum Color
{
Red,
Black
};
template
struct RBTreeNode
{
RBTreeNode(const T& data) 默认构造
:_data(data)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{
;
}
T _data; 节点数据类型根据模板参数而定,可能是一个pair,或者一个key
RBTreeNode*_left;
RBTreeNode* _right;
RBTreeNode* _parent;
Color _color=Red; 默认节点颜色为红
}; 红黑树类
template
class RBTree
{
public:
typedef RBTreeNode Node;
typedef _Iterator iterator;
typedef _Iterator const_iterator; const迭代器,
第一个模板参数不传const T,这个T有大用。
而且const迭代器的不可修改特性是由后面const T*和const T&决定的,与第一个模板参数无关
public:
iterator begin() 树的最左节点是中序遍历的起点
{
Node* cur = _root;
while (cur->_left)
{
cur = cur->_left;
}
return iterator(cur);
}
iterator end() 迭代器++最后到根的parent,也就是空节点
{
return iterator(_root->_parent);
}
const_iterator begin()const
{
Node* cur = _root;
while (cur->_left)
{
cur = cur->_left;
}
const_iterator cit(cur);
return cit;
}
const_iterator end()const
{
return const_iterator(nullptr);
}
public:
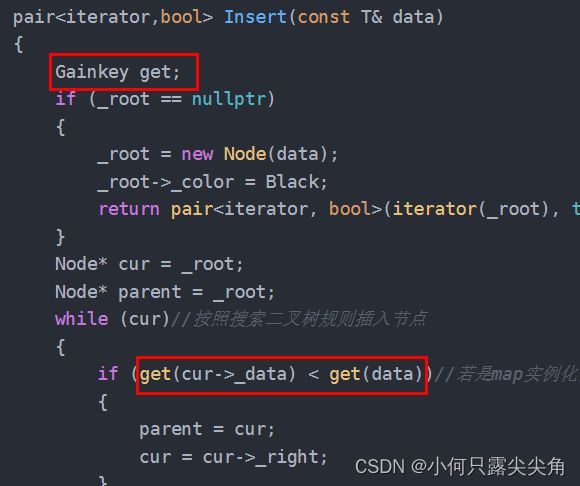
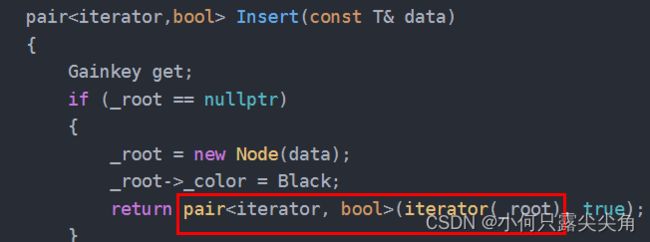
pair Insert(const T& data)
{
Gainkey get;
if (_root == nullptr)
{
_root = new Node(data);
_root->_color = Black;
return pair(iterator(_root), true);
}
Node* cur = _root;
Node* parent = _root;
while (cur) 按照搜索二叉树规则插入节点
{
if (get(cur->_data) < get(data))
若是map实例化,get可以将pair转为key来比较
{
parent = cur;
cur = cur->_right;
}
else if (get(cur->_data) > get(data))
{
parent = cur;
cur = cur->_left;
}
else
{
return pair(iterator(cur), false);
找到相同节点,返回该节点迭代器
}
}
//当cur等于nullptr时,
//插入节点
cur = new Node(data);
Node* newnode = cur;
if (get(parent->_data) > get(data))//小于parent的key,插入到左边
{
parent->_left = cur;
}
else //大于parent的key,插入到右边
{
parent->_right = cur;
}
cur->_parent = parent;
//变色
while (parent && parent->_color == Red)//当cur的父节点为空和颜色为黑时,调整结束
{
Node* gparent = parent->_parent;
if (parent==gparent->_left)
{
Node* uncle = gparent->_right;
if (uncle && uncle->_color==Red)//当uncle节点存在并且颜色为红时
{
uncle->_color = Black;
parent->_color =Black;
gparent->_color = Red;
//继续向上调整
cur = gparent;
parent = cur->_parent;
}
else
{
if (cur == parent->_left)//右单旋
{
RotateR(gparent);
parent->_color = Black;
gparent->_color = Red;
}
if (cur == parent->_right)//双旋
{
RotateL(parent);
RotateR(gparent);
cur->_color = Black;
gparent->_color = Red;
}
break;
}
}
else//parent==gparent->_right
{
Node* uncle = gparent->_left;
if (uncle && uncle->_color == Red)//当uncle节点存在并且颜色为红时
{
uncle->_color = Black;
parent->_color = Black;
gparent->_color = Red;
//继续向上调整
cur = gparent;
parent = cur->_parent;
}
else
{
if (cur == parent->_right)//左单旋
{
RotateL(gparent);
parent->_color = Black;
gparent->_color = Red;
}
if (cur == parent->_left)
{
RotateR(parent);
RotateL(gparent);
cur->_color = Black;
gparent->_color = Red;
}
break;
}
}
}
_root->_color = Black;
return pair(iterator(newnode),true);
}
void RotateR(Node* parent)
{
Node* cur = parent->_left;
Node* Curright = cur->_right;
//旋转
Node* pparent = parent->_parent;//记录该树parent节点的父节点
cur->_right = parent;
parent->_left = Curright;
parent->_parent = cur;
cur->_parent = pparent;
if (Curright)//cur的右子树不为空时
{
Curright->_parent = parent;
}
if (parent == _root)//改变根
{
_root = cur;
}
else//和上一层链接
{
if (pparent->_left == parent)
pparent->_left = cur;
else
pparent->_right = cur;
}
}
void RotateL(Node* parent)//左旋转
{
Node* cur = parent->_right;
Node* Curleft = cur->_left;
//旋转
Node* pparent = parent->_parent;
cur->_left = parent;
parent->_right = Curleft;
parent->_parent = cur;
cur->_parent = pparent;
if (Curleft)//cur的左子树不为空时
{
Curleft->_parent = parent;
}
if (parent == _root)//改变根
{
_root = cur;
}
else//和上一层链接
{
if (pparent->_left == parent)
pparent->_left = cur;
else
pparent->_right = cur;
}
}
Node* _root=nullptr;
}; 迭代器类
我们先前只说了set和map容器如何使得key不可修改,还没看const迭代器的实现,
下面有个构造函数先前提过,是特地为了给普通迭代器构造出const迭代器准备的,当然当迭代器类是实例化成普通迭代器时,此时就是一个拷贝构造,如果是构造const迭代器,那就是一个特殊的构造函数,不过此时构造函数的参数it所在的就是在const_iterator的类域内,就不能访问私有,所以说_node不要用private修饰,就是因为只有同一类域才能访问私有,切记切记,时至今日我才理解这句话的含义。
template
struct _Iterator 封装的是一个节点指针_node
{
typedef _Iterator Self; 命名成self是有原因的,
因为在实现的过程中并不是立刻考虑到要多少个模板参数,如果++,--时返回类型写成这个-Iterator,如果模板参数变了,所有写了Iterator都要改
重命名为self就方便多了
typedef _Iterator iterator;
这个地方就是T的大用处,因为我们set那里要用普通迭代器来构造一个const迭代器,
所以我们在类内要有一个iterator类型能接收普通迭代器。
typedef RBTreeNode Node;
_Iterator(Node*node)
:_node(node)
{
;
}
_Iterator(const iterator& it) _node不可用private修饰
:_node(it._node)
{
;
}
Self& operator--()
{
if (_node->_left)//如果左不为空,就访问左树最右节点
{
Node* cur = _node->_left;
while (cur->_right)
{
cur = cur->_right;
}
_node = cur;
}
else//左为空,向上找cur和parent节点,且parent->_right==cur
{
Node* parent = _node->_parent;
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Self& operator++()//后置++
{
if (_node->_right)//如果右不为空,就访问右树最左节点
{
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_left)//可能只有一个root节点
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return (*this);//返回迭代器,this是一个迭代器类型的指针
}
Self operator++(int)//前置++
{
Self ret = (*this);
if (_node->_right)//如果右不为空,就访问右树最左节点
{
Node* cur = _node->_right;
while (cur->_left)
{
cur = cur->_left;
}
_node = cur;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)//可能只有一个root节点,
//当cur为parent的左节点或者parent为空,循环结束
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return ret;
}
bool operator!=(const Self&data) 比较迭代器是否不同,就看包含节点是否相等
{
return _node != data._node; data是迭代器类型,访问成员用.操作符
}
Ref operator*() 返回节点数据
{
return _node->_data;
}
Ptr operator->() 返回节点数据的地址
{
return &(_node->_data); 只能返回地址
}
Node* _node;
}; 总算写完了,一开始觉得这篇难以下手,写了一两天解决了一个又一个小问题后发现困难越来越小,有时候一件事难度太大,分成一件件小事一件件完成或许成功概率更大。