十月每日一题打卡
每日打卡
10.1 [重新格式化电话号码 lc1694](1694. 重新格式化电话号码 - 力扣(LeetCode))
模拟题:特殊情况就是在最后划分完全部三个之后,还剩四个需要变成aa-bb
class Solution {
public:
string reformatNumber(string number) {
string ans;
queue q;
for(char ch: number)
{
if(ch != ' ' && ch != '-')
q.push(ch);
}
int cnt = 0;
while(q.size())
{
if(cnt == 0 && q.size() == 4)
{
ans += q.front();
q.pop();
ans += q.front();
q.pop();
ans += '-';
ans += q.front();
q.pop();
ans += q.front();
q.pop();
}
if(!q.size())
break;
if(cnt == 3)
{
ans += '-';
cnt = 0;
}
else
{
ans += q.front();
q.pop();
cnt++;
}
}
return ans;
}
};
10.2 [在LR字符串中交换相邻字符 lc 777](777. 在LR字符串中交换相邻字符 - 力扣(LeetCode))
题目的意思是L可以越过X向左移动,R可以越过X向右移动。
!也就是去掉X后start和end字符串的L和R位置相同!
class Solution {
public:
bool canTransform(string start, string end) {
int n = start.size();
int i = 0, j = 0;
while(1)
{
//越过所有的X
while(i < n && start[i] == 'X')
i++;
while(j < n && end[j] == 'X')
j++;
//判断现在的i和j情况
//如果两个都走到底了那可以
if(i == n && j == n)
return true;
//有一个走到底了另一个没有或者二者对应的不相同那不行
if(i == n || j == n || start[i] != end[j])
return false;
//两者的位置不同也不行L可以左移所以start的可以在end后面
if(start[i] == 'L' && i < j)
return false;
//R可以右移所以start的可以在end前面
if(start[i] =='R' && i > j)
return false;
i++;
j++;
}
return true;
}
};
10.2 [每日温度 lc739](739. 每日温度 - 力扣(LeetCode))
单调栈
明显的单调栈就是说维持这个栈单调递减,如果出现比栈顶大的元素,说明下一个更高温度已经出现,可以将其pop出来了。
可以在栈底设置一个哨兵0,这样便于处理边界
class Solution {
public:
vector dailyTemperatures(vector& temp) {
int n = temp.size();
vector ans(n, 0);
stack stk;
stk.push(0);
for(int i = 1; i < n; i++)
{
while(!stk.empty() && temp[stk.top()] < temp[i])
{
ans[stk.top()] = i - stk.top();
stk.pop();
}
stk.push(i);
}
return ans;
}
};
10.3 [检查二进制字符串字段 lc1784](1784. 检查二进制字符串字段 - 力扣(LeetCode))
题目含义很难理解,看了评论区之后:连续若干个"1"组成的字段是由一个或者多个连续‘1’组成的,如果这样的字段不超过1个,就返回true,多于1个就返回false。
1000 true 110001 false 统计即可
class Solution {
public:
bool checkOnesSegment(string s) {
int cnt = 0;
int n = s.size();
int len = 0;
for(int i = 0; i < n; i++)
{
while(i < n && s[i] == '1')
{
len++;
i++;
}
if(len >= 1)
cnt++;
if(i < n && s[i] == '0')
len = 0;
}
return cnt <= 1;
}
};
10.3 [柱状图中的最大矩形 lc 84](84. 柱状图中最大的矩形 - 力扣(LeetCode))
我们之前做过一个类似的,盛最多水的容器,那个是构造的矩形是两个边界中最小即可,也即是双指针就行。这个不一样的是你需要使用整个容器内的最矮的作为高。所以我们想遍历每个柱子,以其作为高h,然后去寻找最宽的边,也即是向两边分别找高于h的柱子,找到第一个低于h的就停止。
这个也是单调栈,对于单调递增的栈来说:栈里的前一个元素就是左边第一个小于该元素的值,右边第一个小于我们可以在比较中得到。当发现小于栈顶元素时就可以得到右边第一个了,否则就加入栈中即可。
class Solution {
public:
int largestRectangleArea(vector& heights) {
int n = heights.size() + 2;
//向两边加一个哨兵
heights.insert(heights.begin(), 0);
heights.push_back(0);
int ans = 0;
stack s;
for(int i = 0; i < n; i++)
{
while(!s.empty() && heights[i] < heights[s.top()])
{
int j = s.top();
s.pop();
ans = max(ans, heights[j] * (i - s.top() - 1));
}
s.push(i);
}
return ans;
}
};
10.3 [最大矩形 lc85](85. 最大矩形 - 力扣(LeetCode))
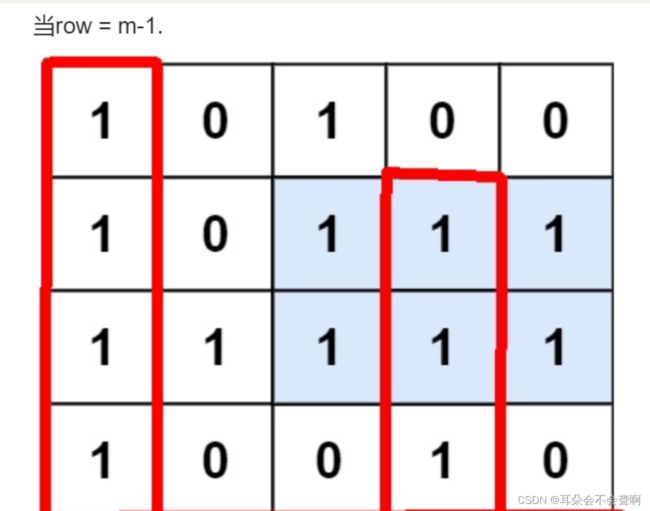
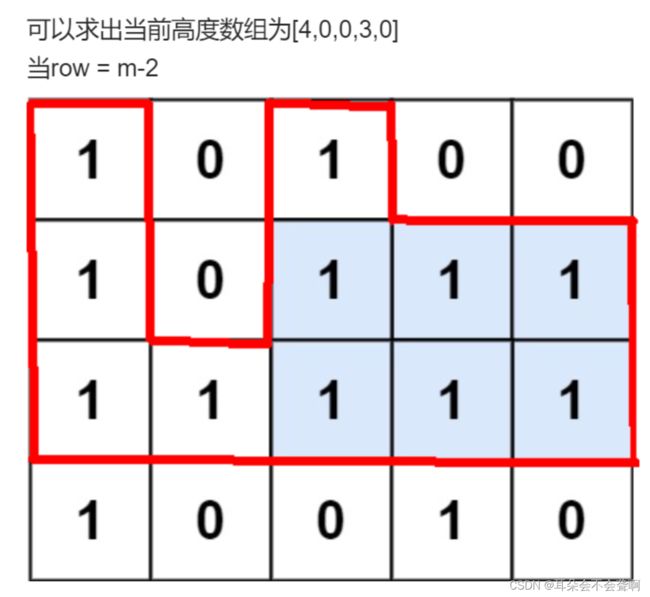
就是上面lc84的二维版本
最形象的图就是这个
只用第一行高度是 1 0 1 0 0
12行高度是 2 0 2 1 1
13行高度是 3 1 3 2 2
这几行分别调用lc84即可取最大即可!
class Solution {
public:
int maximalRectangle(vector>& matrix) {
int row = matrix.size(), col = matrix[0].size();
if(row == 0 || col == 0)
return 0;
int ans = 0;
vector height(col, 0);
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
if(matrix[i][j] == '1')
height[j] = height[j] + 1;
else
height[j] = 0;
}
for(int x: height)
cout << x << " ";
cout << endl;
ans = max(ans, largestRectangleArea(height));
}
return ans;
}
int largestRectangleArea(vector heights) {
int n = heights.size() + 2;
heights.insert(heights.begin(), 0);
heights.push_back(0);
int ans = 0;
stack s;
for(int i = 0; i < n; i++)
{
while(!s.empty() && heights[i] < heights[s.top()])
{
int j = s.top();
s.pop();
ans = max(ans, heights[j] * (i - s.top() - 1));
}
s.push(i);
}
return ans;
}
};
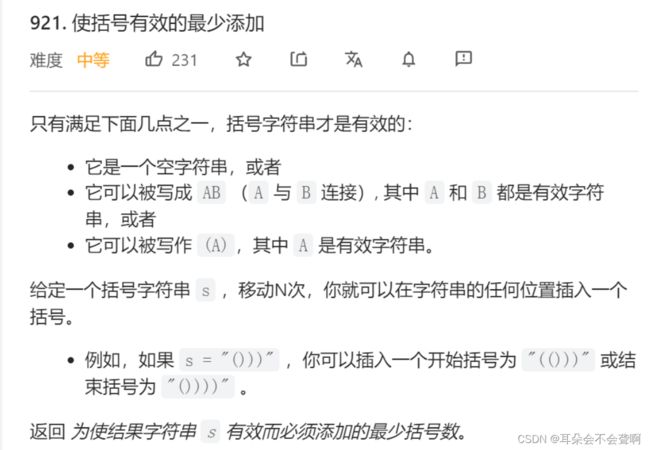
10.4 [使括号有效的最少添加 lc 921](921. 使括号有效的最少添加 - 力扣(LeetCode))
这个就是有效的括号,但是由于是任意位置插入左括号和右括号都行,只需要数量对应上即可。左括号+1,右括号先抵消再计数即可
class Solution {
public:
int minAddToMakeValid(string s) {
int l = 0, cnt = 0;
for(char ch: s)
{
if(ch == '(')
l++;
else if(l > 0 && ch == ')')
l--;
else if(l == 0 && ch == ')')
cnt++;
}
return cnt + l;
}
};
10.4 [最短无序连续子数组 lc 581] (581. 最短无序连续子数组 - 力扣(LeetCode))
这个看起来很简单,本来想着从两边向中间扩展出现无序就停止来着,但是其中的等号很麻烦。这个题一点都不简单。
两个边界l, r。l是最左边需要开始排序的数,应该从右边开始遍历。如果不需要排序的话,那么从右边开始应该每一个数nums[j]都小于等于右边遍历过的min。反之若nums[j] > min的话,就需要记录下来需要排序的值l。
同理,r是最右边需要开始排序的数,应该从左边开始遍历。如果不需要排序的话,那么从左边开始应该每一个数nums[i]都大于等于左边遍历过前i - 1个数的max。反之若nums[j] < max的话,就需要记录下来需要排序的值r。
class Solution {
public:
int findUnsortedSubarray(vector& nums) {
int n = nums.size();
int ma = INT_MIN, mi = INT_MAX;
int l = 0, r = 0;
for(int i = 0; i < n; i++)
{
if(nums[i] < ma)
r = i;
else
ma = max(ma, nums[i]);
}
for(int j = n - 1; j >= 0; j--)
{
if(nums[j] > mi)
l = j;
else
mi = min(mi, nums[j]);
}
if(l == r)
return 0;
else
return r - l + 1;
}
};
10.5 [子域名访问计数 lc 811](811. 子域名访问计数 - 力扣(LeetCode))
简单模拟:使用hashmap的key存储域名,value存储个数,处理字符串计数即可。
class Solution {
public:
vector subdomainVisits(vector& cpdomains) {
unordered_map hashMap;
vector ans;
for(string s: cpdomains)
{
int i = 0;
while(i < s.size() && s[i] != ' ')
i++;
int cnt = atoi(s.substr(0, i).c_str());
string s1 = s.substr(++i); //google.mail.com
if(hashMap.find(s1) != hashMap.end())
hashMap[s1] += cnt;
else
hashMap[s1] = cnt;
while(i < s.size() && s[i] != '.')
i++;
string s2 = s.substr(++i); //mail.com
if(hashMap.find(s2) != hashMap.end())
hashMap[s2] += cnt;
else
hashMap[s2] = cnt;
while(i < s.size() && s[i] != '.')
i++;
if(i < s.size() && s[i] == '.')
{
string s3 = s.substr(++i); //com
if(hashMap.find(s3) != hashMap.end())
hashMap[s3] += cnt;
else
hashMap[s3] = cnt;
}
}
for(auto x: hashMap)
{
string s = to_string(x.second) + " " + x.first;
ans.push_back(s);
}
return ans;
}
};
[10.5 盛最多水的容器 lc 11](11. 盛最多水的容器 - 力扣(LeetCode))
这个就很简单啦,双指针遍历一下
class Solution {
public:
int maxArea(vector& height) {
int n = height.size();
int i = 0, j = n - 1;
int ans = 0;
while(i < j)
{
int s = min(height[i], height[j]) * (j - i);
ans = max(ans, s);
if(height[i] < height[j])
i++;
else
j--;
}
return ans;
}
};
[10.5 删掉链表的倒数第n个节点 lc 19](19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode))
也很简单啦,就是快慢指针先找到倒数第n个节点,然后删除即可。
注意一些边界条件,比如删除头节点、删除只有一个元素的链表等
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* p = head;
if(head->next == nullptr)
return nullptr;
for(int i = 0; i < n; i++)
p = p->next;
ListNode* q = head;
if(p == nullptr)
return head->next; //删掉头节点
while(p->next != nullptr)
{
p = p->next;
q = q->next;
}
ListNode* nx = q->next;
q->next = nx->next;
return head;
}
};
[10.6 三等分 lc 927](927. 三等分 - 力扣(LeetCode))
三个指针判断三部分是否相等,二进制是否相等首先看1的个数,其次看第一个1后的排列是否相等。`
class Solution {
public:
vector threeEqualParts(vector& arr) {
vector ans = {-1, -1};
int n = arr.size();
int cnt = 0;
//求出所有1的数量
for(int i = 0; i < n; i++)
cnt += arr[i];
if(cnt == 0)
return {0, n - 1};
//三者平分 能分继续 不能分就不行
if(cnt % 3) return ans;
cnt = cnt / 3;
int i = 0, j = 0, k = 0, s = 0;
//根据1的数量将三个指针定位到各自第一个1的位置
while(i < n && s < 1) { s += arr[i++];}
s = 0;
while(j < n && s < cnt + 1) { s += arr[j++];}
s = 0;
while(k < n && s < 2 * cnt + 1) { s += arr[k++];}
//开始判断第一个1后面的是否完全相同
while(k < n && arr[i] == arr[j] && arr[j] == arr[k])
{
i++; j++; k++;
}
if(k < n)
return ans;
else
return {i - 1, j};
}
};
[10.6 下一个排列 lc 31](31. 下一个排列 - 力扣(LeetCode))
这个题挺巧妙的,需要仔细分析排列。我们以2 6 3 5 4 1为例,可以从右边开始分析。就是如果是降序比如5 4 1这样的,就是已经是最大的了,不会再有下一个排列了。所以我们第一步需要从右边找第一个升序的,找到了 3 5。为了是下一个排列因此我们需要使这个排列尽可能地小,所以我们从后面5 4 1中选一个第一个比3大地和他交换,得到一个比3大一点的新开头,2 6 4 5 3 1。接下来需要将后面的变成最小的,因为是逆序,所以直接反转即可。
class Solution {
public:
void nextPermutation(vector& nums) {
int n = nums.size();
int i = n - 1;
//找到第一个升序的 3 5
while(i > 0 && nums[i] <= nums[i - 1]) i--;
//如果不存在升序说明全部倒序,直接全部逆序即可
if(i <= 0) {reverse(nums.begin(), nums.end()); return;}
int j = i - 1; // j是3 等着待交换的那个
//向右边倒序序列中找比nums[j]大一点的值 i - 1就是那个4
while(i < n && nums[i] > nums[j]) i++;
cout << nums[j] << " " << nums[i - 1] << endl;
//swap(nums[j], nums[i - 1]); 将二者交换
int t = nums[j];
nums[j] = nums[i - 1];
nums[i - 1] = t;
//最后将后面的倒序逆转变小一点的排列
reverse(nums.begin() + j + 1, nums.end());
}
};
[10.7 最大升序子序列和 lc1800](1800. 最大升序子数组和 - 力扣(LeetCode))
class Solution {
public:
int maxAscendingSum(vector& nums) {
int ans = nums[0], s = nums[0];
for(int i = 1; i < nums.size(); i++)
{
if(nums[i - 1] < nums[i])
s += nums[i];
else
s = nums[i];
ans = max(ans, s);
}
return ans;
}
};
[10.7 寻找重复数 lc 287](287. 寻找重复数 - 力扣(LeetCode))
快慢指针,将1,3,4,2,2看成链表,判断链表是否有环以及找到链表的入口。
class Solution {
public:
int findDuplicate(vector& nums) {
//将数组看成链表,找到环的入口
int slow = 0, fast = 0;
while(1)
{
slow = nums[slow];
fast = nums[nums[fast]];
if(slow == fast)
break;
}
fast = 0;
while(slow != fast)
{
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
[10.7 找到数组中消失的数字 lc 448](448. 找到所有数组中消失的数字 - 力扣(LeetCode))
这个题也是将数组中的值和下标映射起来,比如[4,3,2,7,8,2,3,1],nums[0] = 4,则将4对应的nums[4] = 8换成-8代表有4了,重复的已经成为负数的就不变,最后值为正的下标就是消失的数字。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vector ans;
for(int i = 0; i < nums.size(); i++)
{
nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
}
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] > 0)
ans.push_back(i + 1);
}
return ans;
}
};
[10.8 优势洗牌 lc 870](870. 优势洗牌 - 力扣(LeetCode))
贪心之田忌赛马:在nums1中找大于nums2[i]的最小值,如果没有则返回nums1中的最小值。直接找会导致超时,二分查找第一个。
class Solution {
public:
vector advantageCount(vector& nums1, vector& nums2) {
int n = nums1.size();
vector ans(n, 0);
bool st[n];
int idx = 0;
memset(st, false, sizeof st);
sort(nums1.begin(), nums1.end());
for(int i = 0; i < n; i++)
{
int l = 0, r = n;
while(l < r)
{
int mid = l + r >> 1;
if(nums1[mid] > nums2[i])
r = mid;
else
l = mid + 1;
}
while(l < n && (st[l] || nums1[l] == nums2[i]))
l++;
if(l < n)
{
ans[i] = nums1[l];
st[l] = true;
}
else
{
while(st[idx]) idx++;
ans[i] = nums1[idx];
st[idx++] = true;
}
}
return ans;
}
};
!10.8 三数之和 lc 15
[10.10 数组中第k个元素](215. 数组中的第K个最大元素 - 力扣(LeetCode))
1. 快速排序
快速排序每次都可以使nums[r]== x,然后左侧都小于等于x,右侧都大于等于x。因此只要某次确定值的下标是k就可以返回第k个最大的元素了。
class Solution {
public:
int findKthLargest(vector& nums, int k) {
return quicksort(nums, k, 0, nums.size() - 1);
}
int quicksort(vector& nums, int k, int left, int right)
{
if(right < left)
return INT_MAX;
int x = nums[(left + right) >> 1];
int l = left - 1, r = right + 1;
while(l < r)
{
do l++; while(nums[l] > x);
do r--; while(nums[r] < x);
if(l < r)
{
int t = nums[l]; nums[l] = nums[r]; nums[r] = t;
}
}
int p;
if(nums[l] == x)
p = l;
if(nums[r] == x)
p = r;
if(p == k - 1)
return nums[p];
else if(p > k - 1)
return quicksort(nums, k, left, r);
else
return quicksort(nums, k, r + 1, right);
}
};
2. 建堆
维护一个k长度的小顶堆,堆顶元素就是第k大,当堆顶元素不再是第k大的时候,就调整堆。
最小堆 - 数组中的第K个最大元素 - 力扣(LeetCode)
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int n = nums.size();
make_heap(nums, k);
for(int i = k; i < n; i++)
{
if(nums[i] < nums[0])
continue;
else
{
nums[0] = nums[i];
shift_down(nums, k, 0);
}
}
return nums[0];
}
void shift_down(vector& nums, int k, int i)
{
int j = 2 * i + 1;
while(j < k)
{
if(j + 1 < k && nums[j] > nums[j + 1]) j++;
if(nums[i] > nums[j])
{
swap(nums[i], nums[j]);
i = j;
j = 2 * i + 1;
}
else
break;
}
}
void make_heap(vector& nums, int k)
{
for(int i = k / 2; i >= 0; i--)
shift_down(nums, k, i);
}
};
10.10 使序列递增的最小交换次数 lc 801
状态机dp:dp[i] [0]表示第i位不发生交换使得前i位递增的最小交换次数,1同理。
有两种情况可以交换:
- 两组都满足前后大于,这种就是要不i和i-1都不交换,要么都交换。
- 交叉满足前后大小关系,这种要不i- 1交换要不i交换。
class Solution {
public:
int minSwap(vector& nums1, vector& nums2) {
int n = nums1.size();
int dp[n][2];
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
dp[0][1] = 1;
for(int i = 1; i < n; i++)
{
if(nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1])
{
dp[i][0] = dp[i - 1][0]; //要么不交换
dp[i][1] = dp[i - 1][1] + 1; //要么两个都交换
}
if(nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1])
{
dp[i][0] = min(dp[i][0], dp[i - 1][1]); //前一个发生交换
dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1); //后面这个发生交换
}
}
return min(dp[n - 1][0], dp[n - 1][1]);
}
};
10.11 仅执行一次字符串交换能否使两个字符串相等 lc 1790
记录下两个不同的下标,超过两个不同返回false,最后看不同的两个下标交换后是否相同。
class Solution {
public:
bool areAlmostEqual(string s1, string s2) {
int n = s1.size();
int cnt = 0;
int a[2];
for(int i = 0; i < n; i++)
{
if(s1[i] != s2[i])
{
if(cnt == 2)
{
cnt++;
break;
}
a[cnt++] = i;
}
}
if(cnt == 1 || cnt > 2)
return false;
if(cnt == 0)
return true;
if(s1[a[0]] == s2[a[1]] && s1[a[1]] == s2[a[0]])
return true;
return false;
}
};
10.12 链表组件 lc 817
模拟即可
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
// 被骗了,是求所有组件的个数而不是求组件的最大长度无语无语
int numComponents(ListNode* head, vector& nums) {
int n = nums.size(), ans = 0;
unordered_set hashset;
for(int x: nums)
hashset.insert(x);
ListNode* p = head;
int cnt = 0;
while(p != nullptr)
{
if(hashset.find(p->val) != hashset.end())
cnt++;
else
{
if(cnt)
ans++;
cnt = 0;
}
p = p->next;
}
if(cnt)
ans++;
return ans;
}
};
10.12 接雨水 lc 42
接雨水的关键就是单调栈
不同于柱状图的最大矩形(向两边找低于栈顶的递增),接雨水需要向两边找高于栈顶的,这样才能接住雨水,因此是递减栈。
以栈顶元素作为雨水高度t = height[stk.top()],当右边高于栈顶时,就是找到了右边高于的,然后去找左边高于的,也即是下一个栈顶。还有要是有和栈顶相同的也要pop出去,而且高度要减去。下一个栈顶就是左边高于栈顶的了height[stk.top()]。比较这两边高的选小的作为高,减去t,乘上宽度即可。
class Solution {
public:
int trap(vector& height) {
int n = height.size();
int ans = 0;
stack stk;
for(int i = 0; i < n; i++)
{
while(!stk.empty() && height[i] > height[stk.top()])
{
int t = stk.top();
stk.pop();
while(!stk.empty() && height[stk.top()] == height[t])
stk.pop();
if(!stk.empty())
ans += ( min(height[stk.top()], height[i]) - height[t] ) * (i - stk.top() - 1);
}
stk.push(i);
}
return ans;
}
};
10.13 合并K个升序链表 lc 23
两两归并,最后变成两个合并。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
{
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
if(l1 == nullptr && l2 == nullptr)
return nullptr;
while(l1 != nullptr && l2 != nullptr)
{
if(l1->val < l2->val)
{
p->next = l1;
l1 = l1->next;
}
else
{
p->next = l2;
l2 = l2->next;
}
p = p->next;
}
while(l1 != nullptr)
{
p->next = l1;
l1 = l1->next;
p = p->next;
}
while(l2 != nullptr)
{
p->next = l2;
l2 = l2->next;
p = p->next;
}
return dummy->next;
}
ListNode* binaryMerge(vector& lists, int low, int high)
{
if(low > high)
return nullptr;
if(low == high)
return lists[low];
if(high - low == 1)
return mergeTwoLists(lists[low], lists[high]);
int mid = (low + high) >> 1;
return mergeTwoLists(binaryMerge(lists, low, mid), binaryMerge(lists, mid + 1, high));
}
ListNode* mergeKLists(vector& lists) {
return binaryMerge(lists, 0, lists.size() - 1);
}
};
10.13 找到字符串中所有字母异位词 lc 438
滑动窗口
class Solution {
public:
vector findAnagrams(string s, string p) {
vector ans;
int sn = s.size();
int pn = p.size();
if(pn > sn) return {};
int cnts[26];
int cntp[26];
memset(cnts, 0, sizeof cnts);
memset(cntp, 0, sizeof cntp);
for(int i = 0; i < pn; i++)
cntp[p[i] - 'a']++;
int i = 0, j = 0;
for(; j < pn; j++)
cnts[s[j] - 'a']++;
while(j < sn)
{
bool f = true;
for(int k = 0; k < 26; k++)
{
if(cnts[k] != cntp[k])
f = false;
}
if(f)
ans.push_back(i);
cnts[s[i++] - 'a']--;
if(j < sn)
cnts[s[j++] - 'a']++;
}
bool f = true;
for(int k = 0; k < 26; k++)
{
if(cnts[k] != cntp[k])
f = false;
}
if(f)
ans.push_back(i);
return ans;
}
};
10.13 最多能完成排序的块 lc 769
规律:区间数的最大值小于等于下标就可以分块
class Solution {
public:
int maxChunksToSorted(vector& arr) {
//区间的最大值小于等于索引则可以划分区间
int n = arr.size();
int ans = 0, ma = 0;
for(int i = 0; i < n; i++)
{
if(arr[i] > ma)
ma = arr[i];
if(ma <= i)
{
ans++;
ma = 0;
}
}
return ans;
}
};
10.14 不同的子序列 lc940
题目翻译一下是从s的子序列中选出t的个数
class Solution {
public:
const int mod = 1e9 + 7;
int numDistinct(string s, string t) {
int sn = s.size(), tn = t.size();
int dp[sn + 1][tn + 1];
//dp[i][j]表示st中使用前i个去匹配t中的前j个用的个数
memset(dp, 0, sizeof dp);
for(int i = 0; i <= sn; i++)
dp[i][0] = 1;
for(int i = 1; i <= sn; i++)
{
for(int j = 1; j <= tn; j++)
{
//匹配上了:我们可以选择用不用s[i]去匹配,不用是s[i]是后面可能还有,我们先不用s[i]
if(s[i - 1] == t[j - 1])
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % mod;
else
dp[i][j] = dp[i - 1][j];
}
}
return dp[sn][tn];
}
};
10.14 路径总和 I lc 112
我一开始写的是,先不管下面这个空树是否为空。看[1, 2] 1 这个例子,就是这棵树只有1 ,2 一侧两个节点。在我的判断中走到1这个节点就可以判断true了。但是题目要求的是到叶子节点,所以判断条件要加上节点的左右节点都为空。
//wrong
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr && targetsum == 0)
return true;
if(root == nullptr)
return false;
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
//right
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return false;
if(targetSum == root->val && root->left == nullptr && root->right == nullptr)
return true;
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
10.14 路径总和II lc 113
在1的基础上要记录下满足要求的路径和
class Solution {
public:
vector> ans;
vector tmp;
vector> pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return {};
helper(root, targetSum);
return ans;
}
void helper(TreeNode* root, int targetSum)
{
if(root == nullptr)
return;
if(targetSum == root->val && !root->left && !root->right)
{
tmp.push_back(root->val);
ans.push_back(tmp);
tmp.pop_back();
return ;
}
tmp.push_back(root->val);
helper(root->left, targetSum - root->val);
helper(root->right, targetSum - root->val);
tmp.pop_back();
}
};
10.14 路径总和III lc 437
路径不需要从父节点开始,也不需要在叶子节点结束,但方向要向下。
两个dfs,第一个dfs遍历每个节点,第二dfs去计算和是否满足。
class Solution {
public:
long long ans = 0;
int ts;
int pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return 0;
ts = targetSum;
dfs1(root);
return ans;
}
void dfs1(TreeNode* root)
{
if(root == nullptr)
return;
dfs2(root, 0);
dfs1(root->left);
dfs1(root->right);
}
void dfs2(TreeNode* root, long long curSum)
{
if(root == nullptr)
return;
curSum += root->val;
if(curSum == ts)
ans++;
dfs2(root->left, curSum);
dfs2(root->right, curSum);
}
};
树上的前缀和:哇塞!最完整的路径是从根节点到叶子节点,这题相当于在这些路径上找区间和=targetsum的,那不就是前缀和吗!
curSum - preSum = targetSum即可。
class Solution {
public:
unordered_map preSum;
int targetSum;
int ans = 0;
int pathSum(TreeNode* root, int ts) {
if(root == nullptr)
return 0;
targetSum = ts;
preSum[0] = 1;
dfs(root, 0);
return ans;
}
void dfs(TreeNode* root, long long curSum)
{
if(root == nullptr)
return;
curSum += root->val;
if(preSum.find(curSum - targetSum) != preSum.end())
{
ans += preSum[curSum - targetSum];
}
preSum[curSum]++;
dfs(root->left, curSum);
dfs(root->right, curSum);
preSum[curSum]--;
}
};
10.14 二叉树的序列化与反序列化 lc 297
这道题主要是区分每个节点的值和null处理、负值处理的问题,其他就是递归即可
BFS
class Codec {
public:
const int nll = 2000;
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root == nullptr)
return "";
string data;
queue q;
q.push(root);
while(q.size())
{
TreeNode* tmp = q.front();
q.pop();
if(tmp == nullptr)
{
data += "_#";
continue;
}
data += "_" + to_string(tmp->val);
q.push(tmp->left);
q.push(tmp->right);
}
cout << data << endl;
return data;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data.size() == 0)
return nullptr;
vector v;
int i = 0;
while(i < data.size())
{
int j = i + 1;
while(j < data.size() && data[j] != '_')
j++;
string s = data.substr(i + 1, j - i - 1);
cout << s << endl;
if(s == "#")
v.push_back(nll);
else
v.push_back(atoi(s.c_str()));
i = j;
}
i = 0;
TreeNode* root = new TreeNode(v[i++]);
queue q;
q.push(root);
while(q.size())
{
TreeNode* tmp = q.front();
q.pop();
if(v[i] == nll)
tmp->left = nullptr;
else
{
tmp->left = new TreeNode(v[i]);
q.push(tmp->left);
}
i++;
if(v[i] == nll)
tmp->right = nullptr;
else
{
tmp->right = new TreeNode(v[i]);
q.push(tmp->right);
}
i++;
}
return root;
}
};
DFS
class Codec {
public:
const int nll = 2000;
vector v;
int i = 1;
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root == nullptr)
return "_#";
return "_" + to_string(root->val) + serialize(root->left) + serialize(root->right);
}
void helper(string data)
{
int i = 0;
while(i < data.size())
{
int j = i + 1;
while(j < data.size() && data[j] != '_')
j++;
string s = data.substr(i + 1, j - i - 1);
cout << s << endl;
if(s == "#")
v.push_back(nll);
else
v.push_back(atoi(s.c_str()));
i = j;
}
}
TreeNode* build(TreeNode* root)
{
if(v[i] == nll)
{
root->left = nullptr;
i++;
}
else
{
root->left = new TreeNode(v[i]);
i++;
build(root->left);
}
if(v[i] == nll)
{
root->right = nullptr;
i++;
}
else
{
root->right = new TreeNode(v[i]);
i++;
build(root->right);
}
return root;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data == "_#")
return nullptr;
helper(data);
TreeNode* root = new TreeNode(v[0]);
return build(root);
}
};
10.15 目标和 lc494
1.简单dfs
class Solution {
public:
int n;
//int ans = 0;
int findTargetSumWays(vector& nums, int target) {
n = nums.size();
return dfs(nums, target, 0, 0);
}
int dfs(vector& nums, int target, int curSum, int i)
{
if(i == n && curSum == target)
return 1;
if(i == n)
return 0;
int n1 = dfs(nums, target, curSum + nums[i], i + 1);
int n2 = dfs(nums, target, curSum - nums[i], i + 1);
return n1 + n2;
}
};
2. dfs+记忆化搜索
memo记录的是key = (i, cursum), value=要求的个数
class Solution {
public:
int n;
//int ans = 0;
unordered_map memo;
int findTargetSumWays(vector& nums, int target) {
n = nums.size();
return dfs(nums, target, 0, 0);
}
int dfs(vector& nums, int target, int curSum, int i)
{
string key = to_string(i) + "_" + to_string(curSum);
if(memo.count(key))
return memo[key];
if(i == n && curSum == target)
{
memo[key]++;
return memo[key];
}
if(i == n)
{
memo[key] = 0;
return memo[key];
}
int n1 = dfs(nums, target, curSum + nums[i], i + 1);
int n2 = dfs(nums, target, curSum - nums[i], i + 1);
memo[key] = n1 + n2;
return n1 + n2;
}
};
3. 01背包
在记忆化的基础上变成01背包
class Solution {
public:
int findTargetSumWays(vector& nums, int target) {
int n = nums.size();
int sum = 0;
for(int x: nums)
sum += x;
if(target > sum || target < -sum) return 0;
vector> dp(n + 1, vector(2 * sum + 1, 0));
dp[0][0 + sum] = 1;
for(int i = 1; i <= n; i++)
{
for(int cur = -sum; cur <= sum; cur++)
{
if(cur - nums[i - 1] >= -sum)
dp[i][cur + sum] = dp[i - 1][cur - nums[i - 1] + sum];
if(cur + nums[i - 1] <= sum)
dp[i][cur + sum] += dp[i - 1][cur + nums[i - 1] + sum];
}
}
return dp[n][target + sum];
}
};
10.15 分割等和子集 lc 416
划分两个子集使得x = y,也即是找到一个子集使得x=sum/2。也就是从这些数字中选一些数使得和为sum/2。
01背包问题
class Solution {
public:
int n;
bool canPartition(vector& nums) {
n = nums.size();
int sum = 0;
for(int x: nums)
sum += x;
if(sum % 2) return false;
else return findTargetSumWays(nums, sum / 2);
}
int findTargetSumWays(vector& nums, int target)
{
vector> dp(n + 1, vector(target + 1, false));
for(int i = 0; i <= n; i++)
dp[i][0] = true;
for(int i = 1; i <= n; i++)
{
for(int cur = 0; cur <= target; cur++)
{
dp[i][cur] = dp[i - 1][cur];
if(nums[i - 1] <= cur)
dp[i][cur] = dp[i][cur] || dp[i - 1][cur - nums[i - 1]];
}
}
return dp[n][target];
}
};
!10.15 用栈操作构建数组 lc 1441
!10.16 可能的二分法 lc 886
10.17 完全平方数
还是01背包问题,就是从平方和中选选到和为target的最小数量
class Solution {
public:
const int INF = 0x3f3f3f3f;
int numSquares(int n) {
vector sq;
for(int i = 0; i * i <= n; i++)
sq.push_back(i * i);
int dp[n + 1];
memset(dp, INF, sizeof dp);
dp[1] = 1;
dp[0] = 0;
for(int i = 0; i < sq.size(); i++)
{
for(int j = 0; j <= n; j++)
{
if(sq[i] <= j)
dp[j] = min(dp[j], dp[j - sq[i]] + 1);
}
}
return dp[n];
}
};
10.17 零钱兑换 lc 322
完全背包问题:物品可以无限使用,要求背包装满,要求使用的数量最少。
在满足:amount=v1x1+v2x2+v3x3+…+vnxn 的条件下,求: target=min{x1+x2+x3+…xn}可以dfs将所有的组合拿出来,然后取硬币数最小。
dp[i]表示硬币和为i时的最小硬币数,然后看取不取前i个硬币,取最小即可。
class Solution {
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector& coins, int amount) {
int n = coins.size();
int dp[amount + 1];
memset(dp, INF, sizeof dp);
dp[0] = 0;
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= amount; j++)
{
if(coins[i] <= j)
{
dp[j] = min(dp[j], dp[j - coins[i]] + 1);
}
}
}
if(dp[amount] == INF)
return -1;
else
return dp[amount];
}
};
!10.17 水果成篮 lc 904
!10.18 最大为 N 的数字组合 lc 902
10.18 环形链表 lc 141
快慢指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head == nullptr)
return false;
if(head->next == nullptr)
return false;
ListNode* fast = head;
ListNode* slow = head;
while(fast != nullptr)
{
slow = slow->next;
fast = fast->next;
if(fast != nullptr)
fast = fast->next;
if(slow == fast)
return true;
}
return false;
}
};
10.18 环形链表|| lc 142
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head, *slow = head;
if(head == nullptr) return nullptr;
if(head->next == nullptr) return nullptr;
while(fast != nullptr)
{
slow = slow->next;
fast = fast->next;
if(fast != nullptr)
fast = fast->next;
if(fast == slow)
{
fast = head;
while(fast != slow)
{
fast = fast->next;
slow = slow->next;
}
return fast;
}
}
return nullptr;
}
};
10.18 删除链表的倒数第 N 个结点 lc 19
还是快慢指针找到倒数第n个节点然后再删除~下次再练习
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* p = head;
if(head->next == nullptr)
return nullptr;
for(int i = 0; i < n; i++)
p = p->next;
ListNode* q = head;
if(p == nullptr)
return head->next; //删掉头节点
while(p->next != nullptr)
{
p = p->next;
q = q->next;
}
ListNode* nx = q->next;
q->next = nx->next;
return head;
}
};
!10.19 无法吃午餐肉的同学 lc 1700
!10.19 括号的生成 lc 22
!10.19 组合总和 lc 39
回溯
class Solution {
public:
vector> ans;
vector tmp;
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
dfs(candidates, target, 0, 0);
return ans;
}
void dfs(vector& candidates, int target, int curSum, int i)
{
if(curSum == target)
{
ans.push_back(tmp);
return;
}
if(curSum > target)
{
return;
}
for(int j = i; j < candidates.size(); j++)
{
tmp.push_back(candidates[j]);
dfs(candidates, target, curSum + candidates[j], j);
tmp.pop_back();
}
}
};
!10.19 组合总数 II lc 42
class Solution {
public:
vector> ans;
vector tmp;
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
dfs(candidates, target, 0, 0);
return ans;
}
void dfs(vector& candidates, int target, int cur, int last)
{
if(cur == target)
{
ans.push_back(tmp);
return;
}
if(cur > target)
{
return;
}
for(int i = last; i < candidates.size(); i++)
{
if(i > last && candidates[i] == candidates[i - 1])
continue;
tmp.push_back(candidates[i]);
dfs(candidates, target, cur + candidates[i], i + 1);
tmp.pop_back();
}
}
};
!10.19 电话号码的字母组合 lc 17
10.20 缺失的第一个正数 lc 41
最大的缺失的正数也不会超过nums.size()。还是和下标相关
把每个数放在下标应该在的数上,然后从0开始判断如果和下标不一样的第一个数就是缺失的第一个正数。
class Solution {
public:
int firstMissingPositive(vector& nums) {
int n = nums.size();
for(int i = 0; i < n; i++)
{
while(nums[i] > 0 && nums[i] < n && nums[i] != nums[nums[i] - 1])
swap(nums[i], nums[nums[i] - 1]);
}
for(int i = 0; i < n; i++)
{
if(nums[i] != i + 1)
return i + 1;
}
return n + 1;
}
};
10.20 寻找重复数 lc 287
把数组看成链表,找到环的入口
class Solution {
public:
int findDuplicate(vector& nums) {
//将数组看成链表,找到环的入口
int slow = 0, fast = 0;
while(1)
{
slow = nums[slow];
fast = nums[nums[fast]];
if(slow == fast)
break;
}
fast = 0;
while(slow != fast)
{
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
10.20 找到所有数组中消失的数字 lc 448
就是把出现的数字和下标关联起来,将出现的数字的下标存储的数变成负数,最后是正数的就是缺失的。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vector ans;
for(int i = 0; i < nums.size(); i++)
{
nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
}
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] > 0)
ans.push_back(i + 1);
}
return ans;
}
};
!10.20 第K个语法符号lc 779
!10.21 股票价格跨度 lc 901
!10.22 根据身高重建队列 lc 406
!10.22 规划兼职工作lc 1235
!10.24 除自身以外的乘积 lc 238
!10.24 和为k的子数组 lc 560
!10.24 分割数组 lc 915
!10.25 最短的桥
!10.26 任务调度器 lc 621
!10.26 和至少为k的最短子数组 lc 862
!10.28 戳气球 lc 312
!10.28 子数组的最小值之和 lc 907
10.30 LRU缓存 lc 146
哈希表+ 双向链表:最关键的就是加上一个头节点和尾节点,剩下的就仔细写仔细调试就可以了。
struct Node
{
int key;
int value;
Node* next;
Node* pre;
Node(int k, int v)
{
key = k;
value = v;
next = nullptr;
pre = nullptr;
}
};
class LRUCache {
public:
Node* head;
Node* nail;
int cnt = 0;
int cap;
unordered_map hashmap;
LRUCache(int capacity) {
cap = capacity;
head = new Node(-1, -1);
nail = new Node(-1, -1);
head->next = nail;
head->pre = nail;
nail->next = head;
nail->pre = head;
}
int get(int key) {
if(hashmap.find(key) == hashmap.end())
return -1;
Node* tmp = hashmap[key];
remove(tmp);
addFromHead(tmp);
return tmp->value;
}
void remove(Node* t)
{
hashmap.erase(t->key);
Node* pt = t->pre;
Node* nt = t->next;
pt->next = nt;
nt->pre = pt;
cnt--;
}
void addFromHead(Node* t)
{
hashmap[t->key] = t;
Node* nt = head->next;
t->next = nt;
t->pre = head;
head->next = t;
nt->pre = t;
cnt++;
}
void put(int key, int value) {
if(get(key) != -1)
{
head->next->value = value;
return;
}
if(cnt < cap)
{
Node* tmp = new Node(key, value);
addFromHead(tmp);
}
else
{
Node* tmp = new Node(key, value);
Node* nt = nail->pre;
remove(nt);
addFromHead(tmp);
}
}
};
10.30 字母大小写全排列 lc 784
回溯
class Solution {
public:
vector ans;
string tmp;
vector letterCasePermutation(string s) {
dfs(s, 0);
return ans;
}
void dfs(string s, int i)
{
if(i == s.size())
{
ans.push_back(tmp);
return;
}
if(s[i] >= '0' && s[i] <= '9')
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
}
else if(s[i] >= 'a' && s[i] <= 'z')
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
tmp += (s[i] - 32);
dfs(s, i + 1);
tmp.pop_back();
}
else
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
tmp += (s[i] + 32);
dfs(s, i + 1);
tmp.pop_back();
}
}
};
10.30 最小栈 lc 155
两个栈辅助的
class MinStack {
public:
stack stk;
stack minstack;
MinStack() {
}
void push(int val) {
stk.push(val);
if(minstack.empty() || val <= minstack.top())
minstack.push(val);
}
void pop() {
int x = stk.top();
cout << x << endl;
stk.pop();
if(minstack.size() && x == minstack.top())
minstack.pop();
}
int top() {
return stk.top();
}
int getMin() {
cout << minstack.top() << endl;
return minstack.top();
}
};
链表解决的:头插法,每个节点中记录栈顶当前值和当前值作为栈顶时的最小值。
struct node
{
int val;
int min;
node* next;
node(int x, int y)
{
val = x;
min = y;
next = nullptr;
}
};
class MinStack {
public:
node* head;
MinStack() {
head = nullptr;
}
void push(int val) {
if(head == nullptr)
head = new node(val, val);
else
{
int m = val <= head->min? val: head->min;
node* tmp = new node(val, m);
tmp->next = head;
head = tmp;
}
}
void pop() {
head = head->next;
}
int top() {
return head->val;
}
int getMin() {
return head->min;
}
};
10.31 滑动窗口的最大值 lc 239
模拟滑动窗口不行因为如果排出最大值要重新遍历找最大值,会超时
因此,选择双向队列维护一个单调递减的队列,当删掉的值==左边最大值时,将其删掉.当加入的值大于队尾的值时,删掉队尾维持递减队列.
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
vector ans;
int n = nums.size();
deque q;
int l = 0, r = k - 1;
for(int i = l; i <= r; i++)
{
while(q.size() && nums[i] > q.back())
q.pop_back();
if(!q.size() || nums[i] <= q.back())
q.push_back(nums[i]);
}
ans.push_back(q.front());
while(r + 1 < n)
{
if(q.size() && nums[l] == q.front())
q.pop_front();
while(q.size() && nums[r + 1] > q.back())
q.pop_back();
q.push_back(nums[r + 1]);
ans.push_back(q.front());
l++;
r++;
}
return ans;
}
};
10.31 神奇字符串 lc481
模拟题目即可,小技巧 1^3 = 2 2^3 = 1
class Solution {
public:
int magicalString(int n) {
int x1 = 3, x2 = 3; //x1是总的字符串数量,x2是生成到哪一个
vector s(4, 0);
s[1] = 1; s[2] = 2; s[3] = 2;
int cnt = 1, f = 1;;
while(x1 < n)
{
int t = 0;
if(s[x2] == 1)
{
s.push_back(f);
cnt += (f == 1);
x1++;
}
else
{
s.push_back(f);
s.push_back(f);
x1 += 2;
cnt += (f == 1) * 2;
}
f = f ^ 3;
x2++;
}
if(x1 > n && s[x1] == 1) cnt--;
return cnt;
}
};
10.31 课程表 lc 207
气死我了,一个拓扑排序写了这么久…
const int N = 5010;
int h[N], e[N], ne[N], idx;
void add(int a, int b)
{
e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
}
class Solution {
public:
bool canFinish(int numCourses, vector>& prerequisites) {
//if(prerequisites.size() == 1 && prerequisites[0][0] != p[])
idx = 0;
int cnt = 0;
int inorder[numCourses];
memset(inorder, 0, sizeof inorder);
memset(h, -1, sizeof h);
for(auto x: prerequisites)
{
if(x[0] == x[1])
return false;
add(x[0], x[1]);
inorder[x[1]]++;
}
queue q;
int f = 0;
for(int i = 0; i < numCourses; i++)
{
if(inorder[i] == 0)
{
q.push(i);
inorder[i] = -1;
}
}
while(q.size())
{
int b = q.front();
q.pop();
cnt++;
for(int k = h[b]; k != -1; k = ne[k])
{
int a = e[k];
inorder[a]--;
if(!inorder[a])
q.push(a);
}
}
if(cnt < numCourses)
return false;
else
return true;
}
};
组合题目
1. 与下标相关的
2. 前缀和
3. 01背包
4. 单调栈
一些有的没的
-
字符串转int atoi()但是还需要从string 转到char : s.c_str()
即 int x = atoi(s.c_str());
int转string : string s = to_string(x);
- priority_queue
文章目录
- 每日打卡
-
- 10.1 [重新格式化电话号码 lc1694]([1694. 重新格式化电话号码 - 力扣(LeetCode)](https://leetcode.cn/problems/reformat-phone-number/))
- 10.2 [在LR字符串中交换相邻字符 lc 777]([777. 在LR字符串中交换相邻字符 - 力扣(LeetCode)](https://leetcode.cn/problems/swap-adjacent-in-lr-string/))
- 10.2 [每日温度 lc739]([739. 每日温度 - 力扣(LeetCode)](https://leetcode.cn/problems/daily-temperatures/))
- 10.3 [检查二进制字符串字段 lc1784]([1784. 检查二进制字符串字段 - 力扣(LeetCode)](https://leetcode.cn/problems/check-if-binary-string-has-at-most-one-segment-of-ones/))
- 10.3 [柱状图中的最大矩形 lc 84]([84. 柱状图中最大的矩形 - 力扣(LeetCode)](https://leetcode.cn/problems/largest-rectangle-in-histogram/))
- 10.3 [最大矩形 lc85]([85. 最大矩形 - 力扣(LeetCode)](https://leetcode.cn/problems/maximal-rectangle/))
- 10.4 [使括号有效的最少添加 lc 921]([921. 使括号有效的最少添加 - 力扣(LeetCode)](https://leetcode.cn/problems/minimum-add-to-make-parentheses-valid/))
- 10.4 [最短无序连续子数组 lc 581] ([581. 最短无序连续子数组 - 力扣(LeetCode)](https://leetcode.cn/problems/shortest-unsorted-continuous-subarray/))
- 10.5 [子域名访问计数 lc 811]([811. 子域名访问计数 - 力扣(LeetCode)](https://leetcode.cn/problems/subdomain-visit-count/))
- [10.5 盛最多水的容器 lc 11]([11. 盛最多水的容器 - 力扣(LeetCode)](https://leetcode.cn/problems/container-with-most-water/))
- [10.5 删掉链表的倒数第n个节点 lc 19]([19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)](https://leetcode.cn/problems/remove-nth-node-from-end-of-list/))
- [10.6 三等分 lc 927]([927. 三等分 - 力扣(LeetCode)](https://leetcode.cn/problems/three-equal-parts/))
- [10.6 下一个排列 lc 31]([31. 下一个排列 - 力扣(LeetCode)](https://leetcode.cn/problems/next-permutation/))
- [10.7 最大升序子序列和 lc1800]([1800. 最大升序子数组和 - 力扣(LeetCode)](https://leetcode.cn/problems/maximum-ascending-subarray-sum/))
- [10.7 寻找重复数 lc 287]([287. 寻找重复数 - 力扣(LeetCode)](https://leetcode.cn/problems/find-the-duplicate-number/))
- [10.7 找到数组中消失的数字 lc 448]([448. 找到所有数组中消失的数字 - 力扣(LeetCode)](https://leetcode.cn/problems/find-all-numbers-disappeared-in-an-array/))
- [10.8 优势洗牌 lc 870]([870. 优势洗牌 - 力扣(LeetCode)](https://leetcode.cn/problems/advantage-shuffle/))
- !10.8 三数之和 lc 15
- [10.10 数组中第k个元素]([215. 数组中的第K个最大元素 - 力扣(LeetCode)](https://leetcode.cn/problems/kth-largest-element-in-an-array/submissions/))
-
- 1. 快速排序
- 2. 建堆
- 10.10 使序列递增的最小交换次数 lc 801
- 10.11 仅执行一次字符串交换能否使两个字符串相等 lc 1790
- 10.12 链表组件 lc 817
- 10.12 接雨水 lc 42
- 10.13 合并K个升序链表 lc 23
- 10.13 [找到字符串中所有字母异位词](https://leetcode.cn/problems/find-all-anagrams-in-a-string/) lc 438
- 10.13 最多能完成排序的块 lc 769
- 10.14 不同的子序列 lc940
- 10.14 路径总和 I lc 112
- 10.14 路径总和II lc 113
- 10.14 路径总和III lc 437
- 10.14 二叉树的序列化与反序列化 lc 297
-
- BFS
- DFS
- 10.15 目标和 lc494
-
- 1.简单dfs
- 2. dfs+记忆化搜索
- 3. 01背包
- 10.15 分割等和子集 lc 416
- !10.15 用栈操作构建数组 lc 1441
- !10.16 可能的二分法 lc 886
- 10.17 完全平方数
- 10.17 零钱兑换 lc 322
- !10.17 水果成篮 lc 904
- !10.18 最大为 N 的数字组合 lc 902
- 10.18 环形链表 lc 141
- 10.18 环形链表|| lc 142
- 10.18 删除链表的倒数第 N 个结点 lc 19
- !10.19 无法吃午餐肉的同学 lc 1700
- !10.19 括号的生成 lc 22
- !10.19 组合总和 lc 39
- !10.19 组合总数 II lc 42
- !10.19 电话号码的字母组合 lc 17
- 10.20 缺失的第一个正数 lc 41
- 10.20 寻找重复数 lc 287
- 10.20 找到所有数组中消失的数字 lc 448
- !10.20 第K个语法符号lc 779
- !10.21 股票价格跨度 lc 901
- !10.22 根据身高重建队列 lc 406
- !10.22 规划兼职工作lc 1235
- !10.24 除自身以外的乘积 lc 238
- !10.24 和为k的子数组 lc 560
- !10.24 分割数组 lc 915
- !10.25 最短的桥
- !10.26 任务调度器 lc 621
- !10.26 和至少为k的最短子数组 lc 862
- !10.28 戳气球 lc 312
- !10.28 子数组的最小值之和 lc 907
- 10.30 LRU缓存 lc 146
- 10.30 字母大小写全排列 lc 784
- 10.30 最小栈 lc 155
- 10.31 滑动窗口的最大值 lc 239
- 10.31 神奇字符串 lc481
- 10.31 课程表 lc 207
- 组合题目
-
- 1. 与下标相关的
- 2. 前缀和
- 3. 01背包
- 4. 单调栈
- 一些有的没的
- 每日打卡
-
- 10.1 [重新格式化电话号码 lc1694]([1694. 重新格式化电话号码 - 力扣(LeetCode)](https://leetcode.cn/problems/reformat-phone-number/))
- 10.2 [在LR字符串中交换相邻字符 lc 777]([777. 在LR字符串中交换相邻字符 - 力扣(LeetCode)](https://leetcode.cn/problems/swap-adjacent-in-lr-string/))
- 10.2 [每日温度 lc739]([739. 每日温度 - 力扣(LeetCode)](https://leetcode.cn/problems/daily-temperatures/))
- 10.3 [检查二进制字符串字段 lc1784]([1784. 检查二进制字符串字段 - 力扣(LeetCode)](https://leetcode.cn/problems/check-if-binary-string-has-at-most-one-segment-of-ones/))
- 10.3 [柱状图中的最大矩形 lc 84]([84. 柱状图中最大的矩形 - 力扣(LeetCode)](https://leetcode.cn/problems/largest-rectangle-in-histogram/))
- 10.3 [最大矩形 lc85]([85. 最大矩形 - 力扣(LeetCode)](https://leetcode.cn/problems/maximal-rectangle/))
- 10.4 [使括号有效的最少添加 lc 921]([921. 使括号有效的最少添加 - 力扣(LeetCode)](https://leetcode.cn/problems/minimum-add-to-make-parentheses-valid/))
- 10.4 [最短无序连续子数组 lc 581] ([581. 最短无序连续子数组 - 力扣(LeetCode)](https://leetcode.cn/problems/shortest-unsorted-continuous-subarray/))
- 10.5 [子域名访问计数 lc 811]([811. 子域名访问计数 - 力扣(LeetCode)](https://leetcode.cn/problems/subdomain-visit-count/))
- [10.5 盛最多水的容器 lc 11]([11. 盛最多水的容器 - 力扣(LeetCode)](https://leetcode.cn/problems/container-with-most-water/))
- [10.5 删掉链表的倒数第n个节点 lc 19]([19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)](https://leetcode.cn/problems/remove-nth-node-from-end-of-list/))
- [10.6 三等分 lc 927]([927. 三等分 - 力扣(LeetCode)](https://leetcode.cn/problems/three-equal-parts/))
- [10.6 下一个排列 lc 31]([31. 下一个排列 - 力扣(LeetCode)](https://leetcode.cn/problems/next-permutation/))
- [10.7 最大升序子序列和 lc1800]([1800. 最大升序子数组和 - 力扣(LeetCode)](https://leetcode.cn/problems/maximum-ascending-subarray-sum/))
- [10.7 寻找重复数 lc 287]([287. 寻找重复数 - 力扣(LeetCode)](https://leetcode.cn/problems/find-the-duplicate-number/))
- [10.7 找到数组中消失的数字 lc 448]([448. 找到所有数组中消失的数字 - 力扣(LeetCode)](https://leetcode.cn/problems/find-all-numbers-disappeared-in-an-array/))
- [10.8 优势洗牌 lc 870]([870. 优势洗牌 - 力扣(LeetCode)](https://leetcode.cn/problems/advantage-shuffle/))
- !10.8 三数之和 lc 15
- [10.10 数组中第k个元素]([215. 数组中的第K个最大元素 - 力扣(LeetCode)](https://leetcode.cn/problems/kth-largest-element-in-an-array/submissions/))
-
- 1. 快速排序
- 2. 建堆
- 10.10 使序列递增的最小交换次数 lc 801
- 10.11 仅执行一次字符串交换能否使两个字符串相等 lc 1790
- 10.12 链表组件 lc 817
- 10.12 接雨水 lc 42
- 10.13 合并K个升序链表 lc 23
- 10.13 [找到字符串中所有字母异位词](https://leetcode.cn/problems/find-all-anagrams-in-a-string/) lc 438
- 10.13 最多能完成排序的块 lc 769
- !10.14 不同的子序列 lc940
- 10.14 路径总和 I lc 112
- 10.14 路径总和II lc 113
- 10.14 路径总和III lc 437
- 10.14 二叉树的序列化与反序列化 lc 297
-
- BFS
- DFS
- 10.15 目标和 lc494
-
- 1.简单dfs
- 2. dfs+记忆化搜索
- 3. 01背包
- 10.15 分割等和子集 lc 416
- !10.15 用栈操作构建数组 lc 1441
- !10.16 可能的二分法 lc 886
- 10.17 完全平方数
- 10.17 零钱兑换 lc 322
- !10.17 水果成篮 lc 904
- !10.18 最大为 N 的数字组合 lc 902
- 10.18 环形链表 lc 141
- 10.18 环形链表|| lc 142
- 10.18 删除链表的倒数第 N 个结点 lc 19
- 10.19 无法吃午餐肉的同学 lc 1700
- 10.19 括号的生成 lc 22
- 10.19 组合总和 lc 39
- 10.19 组合总数 II lc 40
- 10.19 电话号码的字母组合 lc 17
- 10.20 缺失的第一个正数 lc 41
- 10.20 寻找重复数 lc 287
- 10.20 找到所有数组中消失的数字 lc 448
- 10.20 第K个语法符号lc 779
- 10.21 股票价格跨度 lc 901
- 10.22 根据身高重建队列 lc 406
- 10.22 规划兼职工作lc 1235
- 10.24 除自身以外的乘积 lc 238
- 10.24 和为k的子数组 lc 560
- 10.24 分割数组 lc 915
- 10.25 最短的桥 934
- 10.26 任务调度器 lc 621
- 10.26 和至少为k的最短子数组 lc 862
- 10.28 戳气球 lc 312
- 10.28 子数组的最小值之和 lc 907
- 10.30 LRU缓存 lc 146
- 10.30 字母大小写全排列 lc 784
- 10.30 最小栈 lc 155
- 10.31 滑动窗口的最大值 lc 239
- 10.31 神奇字符串 lc481
- 10.31 课程表 lc 207
- 一些有的没的
每日打卡
10.1 [重新格式化电话号码 lc1694](1694. 重新格式化电话号码 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wAvE3rWA-1668235849917)(10_leetcode.assets/image-20221004181510443.png)]
模拟题:特殊情况就是在最后划分完全部三个之后,还剩四个需要变成aa-bb
class Solution {
public:
string reformatNumber(string number) {
string ans;
queue q;
for(char ch: number)
{
if(ch != ' ' && ch != '-')
q.push(ch);
}
int cnt = 0;
while(q.size())
{
if(cnt == 0 && q.size() == 4)
{
ans += q.front();
q.pop();
ans += q.front();
q.pop();
ans += '-';
ans += q.front();
q.pop();
ans += q.front();
q.pop();
}
if(!q.size())
break;
if(cnt == 3)
{
ans += '-';
cnt = 0;
}
else
{
ans += q.front();
q.pop();
cnt++;
}
}
return ans;
}
};
10.2 [在LR字符串中交换相邻字符 lc 777](777. 在LR字符串中交换相邻字符 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6UBeYqNz-1668235849918)(10_leetcode.assets/image-20221004182709177.png)]
题目的意思是L可以越过X向左移动,R可以越过X向右移动。
!也就是去掉X后start和end字符串的L和R位置相同!
class Solution {
public:
bool canTransform(string start, string end) {
int n = start.size();
int i = 0, j = 0;
while(1)
{
//越过所有的X
while(i < n && start[i] == 'X')
i++;
while(j < n && end[j] == 'X')
j++;
//判断现在的i和j情况
//如果两个都走到底了那可以
if(i == n && j == n)
return true;
//有一个走到底了另一个没有或者二者对应的不相同那不行
if(i == n || j == n || start[i] != end[j])
return false;
//两者的位置不同也不行L可以左移所以start的可以在end后面
if(start[i] == 'L' && i < j)
return false;
//R可以右移所以start的可以在end前面
if(start[i] =='R' && i > j)
return false;
i++;
j++;
}
return true;
}
};
10.2 [每日温度 lc739](739. 每日温度 - 力扣(LeetCode))
单调栈
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iCARaYR0-1668235849919)(10_leetcode.assets/image-20221005202544978.png)]
明显的单调栈就是说维持这个栈单调递减,如果出现比栈顶大的元素,说明下一个更高温度已经出现,可以将其pop出来了。
可以在栈底设置一个哨兵0,这样便于处理边界
class Solution {
public:
vector dailyTemperatures(vector& temp) {
int n = temp.size();
vector ans(n, 0);
stack stk;
stk.push(0);
for(int i = 1; i < n; i++)
{
while(!stk.empty() && temp[stk.top()] < temp[i])
{
ans[stk.top()] = i - stk.top();
stk.pop();
}
stk.push(i);
}
return ans;
}
};
10.3 [检查二进制字符串字段 lc1784](1784. 检查二进制字符串字段 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qbh8LXzL-1668235849919)(10_leetcode.assets/image-20221005203538687.png)]
题目含义很难理解,看了评论区之后:连续若干个"1"组成的字段是由一个或者多个连续‘1’组成的,如果这样的字段不超过1个,就返回true,多于1个就返回false。
1000 true 110001 false 统计即可
class Solution {
public:
bool checkOnesSegment(string s) {
int cnt = 0;
int n = s.size();
int len = 0;
for(int i = 0; i < n; i++)
{
while(i < n && s[i] == '1')
{
len++;
i++;
}
if(len >= 1)
cnt++;
if(i < n && s[i] == '0')
len = 0;
}
return cnt <= 1;
}
};
10.3 [柱状图中的最大矩形 lc 84](84. 柱状图中最大的矩形 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oaM2Udkf-1668235849920)(10_leetcode.assets/image-20221005203952026.png)]
我们之前做过一个类似的,盛最多水的容器,那个是构造的矩形是两个边界中最小即可,也即是双指针就行。这个不一样的是你需要使用整个容器内的最矮的作为高。所以我们想遍历每个柱子,以其作为高h,然后去寻找最宽的边,也即是向两边分别找高于h的柱子,找到第一个低于h的就停止。
这个也是单调栈,对于单调递增的栈来说:栈里的前一个元素就是左边第一个小于该元素的值,右边第一个小于我们可以在比较中得到。当发现小于栈顶元素时就可以得到右边第一个了,否则就加入栈中即可。
class Solution {
public:
int largestRectangleArea(vector& heights) {
int n = heights.size() + 2;
//向两边加一个哨兵
heights.insert(heights.begin(), 0);
heights.push_back(0);
int ans = 0;
stack s;
for(int i = 0; i < n; i++)
{
while(!s.empty() && heights[i] < heights[s.top()])
{
int j = s.top();
s.pop();
ans = max(ans, heights[j] * (i - s.top() - 1));
}
s.push(i);
}
return ans;
}
};
10.3 [最大矩形 lc85](85. 最大矩形 - 力扣(LeetCode))
就是上面lc84的二维版本
最形象的图就是这个
只用第一行高度是 1 0 1 0 0
12行高度是 2 0 2 1 1
13行高度是 3 1 3 2 2
这几行分别调用lc84即可取最大即可!
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vA50RrVH-1668235849921)(10_leetcode.assets/image-20221005214334845.png)]
class Solution {
public:
int maximalRectangle(vector>& matrix) {
int row = matrix.size(), col = matrix[0].size();
if(row == 0 || col == 0)
return 0;
int ans = 0;
vector height(col, 0);
for(int i = 0; i < row; i++)
{
for(int j = 0; j < col; j++)
{
if(matrix[i][j] == '1')
height[j] = height[j] + 1;
else
height[j] = 0;
}
for(int x: height)
cout << x << " ";
cout << endl;
ans = max(ans, largestRectangleArea(height));
}
return ans;
}
int largestRectangleArea(vector heights) {
int n = heights.size() + 2;
heights.insert(heights.begin(), 0);
heights.push_back(0);
int ans = 0;
stack s;
for(int i = 0; i < n; i++)
{
while(!s.empty() && heights[i] < heights[s.top()])
{
int j = s.top();
s.pop();
ans = max(ans, heights[j] * (i - s.top() - 1));
}
s.push(i);
}
return ans;
}
};
10.4 [使括号有效的最少添加 lc 921](921. 使括号有效的最少添加 - 力扣(LeetCode))
这个就是有效的括号,但是由于是任意位置插入左括号和右括号都行,只需要数量对应上即可。左括号+1,右括号先抵消再计数即可
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0DCDvQ0T-1668235849922)(10_leetcode.assets/image-20221005214634211.png)]
class Solution {
public:
int minAddToMakeValid(string s) {
int l = 0, cnt = 0;
for(char ch: s)
{
if(ch == '(')
l++;
else if(l > 0 && ch == ')')
l--;
else if(l == 0 && ch == ')')
cnt++;
}
return cnt + l;
}
};
10.4 [最短无序连续子数组 lc 581] (581. 最短无序连续子数组 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PgaH4OOF-1668235849922)(10_leetcode.assets/image-20221005214906449.png)]
这个看起来很简单,本来想着从两边向中间扩展出现无序就停止来着,但是其中的等号很麻烦。这个题一点都不简单。
两个边界l, r。l是最左边需要开始排序的数,应该从右边开始遍历。如果不需要排序的话,那么从右边开始应该每一个数nums[j]都小于等于右边遍历过的min。反之若nums[j] > min的话,就需要记录下来需要排序的值l。
同理,r是最右边需要开始排序的数,应该从左边开始遍历。如果不需要排序的话,那么从左边开始应该每一个数nums[i]都大于等于左边遍历过前i - 1个数的max。反之若nums[j] < max的话,就需要记录下来需要排序的值r。
class Solution {
public:
int findUnsortedSubarray(vector& nums) {
int n = nums.size();
int ma = INT_MIN, mi = INT_MAX;
int l = 0, r = 0;
for(int i = 0; i < n; i++)
{
if(nums[i] < ma)
r = i;
else
ma = max(ma, nums[i]);
}
for(int j = n - 1; j >= 0; j--)
{
if(nums[j] > mi)
l = j;
else
mi = min(mi, nums[j]);
}
if(l == r)
return 0;
else
return r - l + 1;
}
};
10.5 [子域名访问计数 lc 811](811. 子域名访问计数 - 力扣(LeetCode))
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JJIdJMUp-1668235849923)(10_leetcode.assets/image-20221005210843421.png)]
简单模拟:使用hashmap的key存储域名,value存储个数,处理字符串计数即可。
class Solution {
public:
vector subdomainVisits(vector& cpdomains) {
unordered_map hashMap;
vector ans;
for(string s: cpdomains)
{
int i = 0;
while(i < s.size() && s[i] != ' ')
i++;
int cnt = atoi(s.substr(0, i).c_str());
string s1 = s.substr(++i); //google.mail.com
if(hashMap.find(s1) != hashMap.end())
hashMap[s1] += cnt;
else
hashMap[s1] = cnt;
while(i < s.size() && s[i] != '.')
i++;
string s2 = s.substr(++i); //mail.com
if(hashMap.find(s2) != hashMap.end())
hashMap[s2] += cnt;
else
hashMap[s2] = cnt;
while(i < s.size() && s[i] != '.')
i++;
if(i < s.size() && s[i] == '.')
{
string s3 = s.substr(++i); //com
if(hashMap.find(s3) != hashMap.end())
hashMap[s3] += cnt;
else
hashMap[s3] = cnt;
}
}
for(auto x: hashMap)
{
string s = to_string(x.second) + " " + x.first;
ans.push_back(s);
}
return ans;
}
};
[10.5 盛最多水的容器 lc 11](11. 盛最多水的容器 - 力扣(LeetCode))
这个就很简单啦,双指针遍历一下
class Solution {
public:
int maxArea(vector& height) {
int n = height.size();
int i = 0, j = n - 1;
int ans = 0;
while(i < j)
{
int s = min(height[i], height[j]) * (j - i);
ans = max(ans, s);
if(height[i] < height[j])
i++;
else
j--;
}
return ans;
}
};
[10.5 删掉链表的倒数第n个节点 lc 19](19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode))
也很简单啦,就是快慢指针先找到倒数第n个节点,然后删除即可。
注意一些边界条件,比如删除头节点、删除只有一个元素的链表等
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* p = head;
if(head->next == nullptr)
return nullptr;
for(int i = 0; i < n; i++)
p = p->next;
ListNode* q = head;
if(p == nullptr)
return head->next; //删掉头节点
while(p->next != nullptr)
{
p = p->next;
q = q->next;
}
ListNode* nx = q->next;
q->next = nx->next;
return head;
}
};
[10.6 三等分 lc 927](927. 三等分 - 力扣(LeetCode))
三个指针判断三部分是否相等,二进制是否相等首先看1的个数,其次看第一个1后的排列是否相等。`
class Solution {
public:
vector threeEqualParts(vector& arr) {
vector ans = {-1, -1};
int n = arr.size();
int cnt = 0;
//求出所有1的数量
for(int i = 0; i < n; i++)
cnt += arr[i];
if(cnt == 0)
return {0, n - 1};
//三者平分 能分继续 不能分就不行
if(cnt % 3) return ans;
cnt = cnt / 3;
int i = 0, j = 0, k = 0, s = 0;
//根据1的数量将三个指针定位到各自第一个1的位置
while(i < n && s < 1) { s += arr[i++];}
s = 0;
while(j < n && s < cnt + 1) { s += arr[j++];}
s = 0;
while(k < n && s < 2 * cnt + 1) { s += arr[k++];}
//开始判断第一个1后面的是否完全相同
while(k < n && arr[i] == arr[j] && arr[j] == arr[k])
{
i++; j++; k++;
}
if(k < n)
return ans;
else
return {i - 1, j};
}
};
[10.6 下一个排列 lc 31](31. 下一个排列 - 力扣(LeetCode))
这个题挺巧妙的,需要仔细分析排列。我们以2 6 3 5 4 1为例,可以从右边开始分析。就是如果是降序比如5 4 1这样的,就是已经是最大的了,不会再有下一个排列了。所以我们第一步需要从右边找第一个升序的,找到了 3 5。为了是下一个排列因此我们需要使这个排列尽可能地小,所以我们从后面5 4 1中选一个第一个比3大地和他交换,得到一个比3大一点的新开头,2 6 4 5 3 1。接下来需要将后面的变成最小的,因为是逆序,所以直接反转即可。
class Solution {
public:
void nextPermutation(vector& nums) {
int n = nums.size();
int i = n - 1;
//找到第一个升序的 3 5
while(i > 0 && nums[i] <= nums[i - 1]) i--;
//如果不存在升序说明全部倒序,直接全部逆序即可
if(i <= 0) {reverse(nums.begin(), nums.end()); return;}
int j = i - 1; // j是3 等着待交换的那个
//向右边倒序序列中找比nums[j]大一点的值 i - 1就是那个4
while(i < n && nums[i] > nums[j]) i++;
cout << nums[j] << " " << nums[i - 1] << endl;
//swap(nums[j], nums[i - 1]); 将二者交换
int t = nums[j];
nums[j] = nums[i - 1];
nums[i - 1] = t;
//最后将后面的倒序逆转变小一点的排列
reverse(nums.begin() + j + 1, nums.end());
}
};
[10.7 最大升序子序列和 lc1800](1800. 最大升序子数组和 - 力扣(LeetCode))
class Solution {
public:
int maxAscendingSum(vector& nums) {
int ans = nums[0], s = nums[0];
for(int i = 1; i < nums.size(); i++)
{
if(nums[i - 1] < nums[i])
s += nums[i];
else
s = nums[i];
ans = max(ans, s);
}
return ans;
}
};
[10.7 寻找重复数 lc 287](287. 寻找重复数 - 力扣(LeetCode))
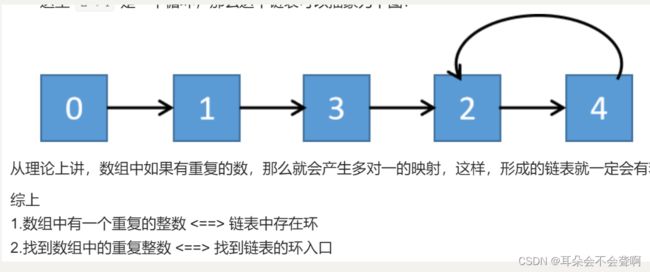
快慢指针,将1,3,4,2,2看成链表,判断链表是否有环以及找到链表的入口。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YWXcDYdd-1668235849923)(10_leetcode.assets/image-20221018001113229.png)]
class Solution {
public:
int findDuplicate(vector& nums) {
//将数组看成链表,找到环的入口
int slow = 0, fast = 0;
while(1)
{
slow = nums[slow];
fast = nums[nums[fast]];
if(slow == fast)
break;
}
fast = 0;
while(slow != fast)
{
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
[10.7 找到数组中消失的数字 lc 448](448. 找到所有数组中消失的数字 - 力扣(LeetCode))
这个题也是将数组中的值和下标映射起来,比如[4,3,2,7,8,2,3,1],nums[0] = 4,则将4对应的nums[4] = 8换成-8代表有4了,重复的已经成为负数的就不变,最后值为正的下标就是消失的数字。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vector ans;
for(int i = 0; i < nums.size(); i++)
{
nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
}
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] > 0)
ans.push_back(i + 1);
}
return ans;
}
};
[10.8 优势洗牌 lc 870](870. 优势洗牌 - 力扣(LeetCode))
贪心之田忌赛马:在nums1中找大于nums2[i]的最小值,如果没有则返回nums1中的最小值。直接找会导致超时,二分查找第一个。
class Solution {
public:
vector advantageCount(vector& nums1, vector& nums2) {
int n = nums1.size();
vector ans(n, 0);
bool st[n];
int idx = 0;
memset(st, false, sizeof st);
sort(nums1.begin(), nums1.end());
for(int i = 0; i < n; i++)
{
int l = 0, r = n;
while(l < r)
{
int mid = l + r >> 1;
if(nums1[mid] > nums2[i])
r = mid;
else
l = mid + 1;
}
while(l < n && (st[l] || nums1[l] == nums2[i]))
l++;
if(l < n)
{
ans[i] = nums1[l];
st[l] = true;
}
else
{
while(st[idx]) idx++;
ans[i] = nums1[idx];
st[idx++] = true;
}
}
return ans;
}
};
!10.8 三数之和 lc 15
[10.10 数组中第k个元素](215. 数组中的第K个最大元素 - 力扣(LeetCode))
1. 快速排序
快速排序每次都可以使nums[r]== x,然后左侧都小于等于x,右侧都大于等于x。因此只要某次确定值的下标是k就可以返回第k个最大的元素了。
class Solution {
public:
int findKthLargest(vector& nums, int k) {
return quicksort(nums, k, 0, nums.size() - 1);
}
int quicksort(vector& nums, int k, int left, int right)
{
if(right < left)
return INT_MAX;
int x = nums[(left + right) >> 1];
int l = left - 1, r = right + 1;
while(l < r)
{
do l++; while(nums[l] > x);
do r--; while(nums[r] < x);
if(l < r)
{
int t = nums[l]; nums[l] = nums[r]; nums[r] = t;
}
}
int p;
if(nums[l] == x)
p = l;
if(nums[r] == x)
p = r;
if(p == k - 1)
return nums[p];
else if(p > k - 1)
return quicksort(nums, k, left, r);
else
return quicksort(nums, k, r + 1, right);
}
};
2. 建堆
维护一个k长度的小顶堆,堆顶元素就是第k大,当堆顶元素不再是第k大的时候,就调整堆。
最小堆 - 数组中的第K个最大元素 - 力扣(LeetCode)
class Solution {
public:
int findKthLargest(vector& nums, int k) {
int n = nums.size();
make_heap(nums, k);
for(int i = k; i < n; i++)
{
if(nums[i] < nums[0])
continue;
else
{
nums[0] = nums[i];
shift_down(nums, k, 0);
}
}
return nums[0];
}
void shift_down(vector& nums, int k, int i)
{
int j = 2 * i + 1;
while(j < k)
{
if(j + 1 < k && nums[j] > nums[j + 1]) j++;
if(nums[i] > nums[j])
{
swap(nums[i], nums[j]);
i = j;
j = 2 * i + 1;
}
else
break;
}
}
void make_heap(vector& nums, int k)
{
for(int i = k / 2; i >= 0; i--)
shift_down(nums, k, i);
}
};
10.10 使序列递增的最小交换次数 lc 801
状态机dp:dp[i] [0]表示第i位不发生交换使得前i位递增的最小交换次数,1同理。
有两种情况可以交换:
- 两组都满足前后大于,这种就是要不i和i-1都不交换,要么都交换。
- 交叉满足前后大小关系,这种要不i- 1交换要不i交换。
class Solution {
public:
int minSwap(vector& nums1, vector& nums2) {
int n = nums1.size();
int dp[n][2];
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
dp[0][1] = 1;
for(int i = 1; i < n; i++)
{
if(nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1])
{
dp[i][0] = dp[i - 1][0]; //要么不交换
dp[i][1] = dp[i - 1][1] + 1; //要么两个都交换
}
if(nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1])
{
dp[i][0] = min(dp[i][0], dp[i - 1][1]); //前一个发生交换
dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1); //后面这个发生交换
}
}
return min(dp[n - 1][0], dp[n - 1][1]);
}
};
10.11 仅执行一次字符串交换能否使两个字符串相等 lc 1790
记录下两个不同的下标,超过两个不同返回false,最后看不同的两个下标交换后是否相同。
class Solution {
public:
bool areAlmostEqual(string s1, string s2) {
int n = s1.size();
int cnt = 0;
int a[2];
for(int i = 0; i < n; i++)
{
if(s1[i] != s2[i])
{
if(cnt == 2)
{
cnt++;
break;
}
a[cnt++] = i;
}
}
if(cnt == 1 || cnt > 2)
return false;
if(cnt == 0)
return true;
if(s1[a[0]] == s2[a[1]] && s1[a[1]] == s2[a[0]])
return true;
return false;
}
};
10.12 链表组件 lc 817
模拟即可
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
// 被骗了,是求所有组件的个数而不是求组件的最大长度无语无语
int numComponents(ListNode* head, vector& nums) {
int n = nums.size(), ans = 0;
unordered_set hashset;
for(int x: nums)
hashset.insert(x);
ListNode* p = head;
int cnt = 0;
while(p != nullptr)
{
if(hashset.find(p->val) != hashset.end())
cnt++;
else
{
if(cnt)
ans++;
cnt = 0;
}
p = p->next;
}
if(cnt)
ans++;
return ans;
}
};
10.12 接雨水 lc 42
接雨水的关键就是单调栈
不同于柱状图的最大矩形(向两边找低于栈顶的递增),接雨水需要向两边找高于栈顶的,这样才能接住雨水,因此是递减栈。
以栈顶元素作为雨水高度t = height[stk.top()],当右边高于栈顶时,就是找到了右边高于的,然后去找左边高于的,也即是下一个栈顶。还有要是有和栈顶相同的也要pop出去,而且高度要减去。下一个栈顶就是左边高于栈顶的了height[stk.top()]。比较这两边高的选小的作为高,减去t,乘上宽度即可。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-b9ehoulr-1668235849924)(10_leetcode.assets/image-20221021204205650.png)]
class Solution {
public:
int trap(vector& height) {
int n = height.size();
int ans = 0;
stack stk;
for(int i = 0; i < n; i++)
{
while(!stk.empty() && height[i] > height[stk.top()])
{
int t = stk.top();
stk.pop();
while(!stk.empty() && height[stk.top()] == height[t])
stk.pop();
if(!stk.empty())
ans += ( min(height[stk.top()], height[i]) - height[t] ) * (i - stk.top() - 1);
}
stk.push(i);
}
return ans;
}
};
10.13 合并K个升序链表 lc 23
两两归并,最后变成两个合并。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2)
{
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
if(l1 == nullptr && l2 == nullptr)
return nullptr;
while(l1 != nullptr && l2 != nullptr)
{
if(l1->val < l2->val)
{
p->next = l1;
l1 = l1->next;
}
else
{
p->next = l2;
l2 = l2->next;
}
p = p->next;
}
while(l1 != nullptr)
{
p->next = l1;
l1 = l1->next;
p = p->next;
}
while(l2 != nullptr)
{
p->next = l2;
l2 = l2->next;
p = p->next;
}
return dummy->next;
}
ListNode* binaryMerge(vector& lists, int low, int high)
{
if(low > high)
return nullptr;
if(low == high)
return lists[low];
if(high - low == 1)
return mergeTwoLists(lists[low], lists[high]);
int mid = (low + high) >> 1;
return mergeTwoLists(binaryMerge(lists, low, mid), binaryMerge(lists, mid + 1, high));
}
ListNode* mergeKLists(vector& lists) {
return binaryMerge(lists, 0, lists.size() - 1);
}
};
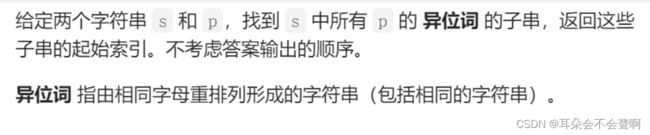
10.13 找到字符串中所有字母异位词 lc 438
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-qDfP7fK1-1668235849933)(image-20221027234642721.png)]
滑动窗口
class Solution {
public:
vector findAnagrams(string s, string p) {
vector ans;
int sn = s.size();
int pn = p.size();
if(pn > sn) return {};
int cnts[26];
int cntp[26];
memset(cnts, 0, sizeof cnts);
memset(cntp, 0, sizeof cntp);
for(int i = 0; i < pn; i++)
cntp[p[i] - 'a']++;
int i = 0, j = 0;
for(; j < pn; j++)
cnts[s[j] - 'a']++;
while(j < sn)
{
bool f = true;
for(int k = 0; k < 26; k++)
{
if(cnts[k] != cntp[k])
f = false;
}
if(f)
ans.push_back(i);
cnts[s[i++] - 'a']--;
if(j < sn)
cnts[s[j++] - 'a']++;
}
bool f = true;
for(int k = 0; k < 26; k++)
{
if(cnts[k] != cntp[k])
f = false;
}
if(f)
ans.push_back(i);
return ans;
}
};
10.13 最多能完成排序的块 lc 769
规律:区间数的最大值小于等于下标就可以分块
class Solution {
public:
int maxChunksToSorted(vector& arr) {
//区间的最大值小于等于索引则可以划分区间
int n = arr.size();
int ans = 0, ma = 0;
for(int i = 0; i < n; i++)
{
if(arr[i] > ma)
ma = arr[i];
if(ma <= i)
{
ans++;
ma = 0;
}
}
return ans;
}
};
!10.14 不同的子序列 lc940
10.14 路径总和 I lc 112
我一开始写的是,先不管下面这个空树是否为空。看[1, 2] 1 这个例子,就是这棵树只有1 ,2 一侧两个节点。在我的判断中走到1这个节点就可以判断true了。但是题目要求的是到叶子节点,所以判断条件要加上节点的左右节点都为空。
//wrong
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr && targetsum == 0)
return true;
if(root == nullptr)
return false;
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
//right
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return false;
if(targetSum == root->val && root->left == nullptr && root->right == nullptr)
return true;
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
10.14 路径总和II lc 113
在1的基础上要记录下满足要求的路径和
class Solution {
public:
vector> ans;
vector tmp;
vector> pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return {};
helper(root, targetSum);
return ans;
}
void helper(TreeNode* root, int targetSum)
{
if(root == nullptr)
return;
if(targetSum == root->val && !root->left && !root->right)
{
tmp.push_back(root->val);
ans.push_back(tmp);
tmp.pop_back();
return ;
}
tmp.push_back(root->val);
helper(root->left, targetSum - root->val);
helper(root->right, targetSum - root->val);
tmp.pop_back();
}
};
10.14 路径总和III lc 437
路径不需要从父节点开始,也不需要在叶子节点结束,但方向要向下。
两个dfs,第一个dfs遍历每个节点,第二dfs去计算和是否满足。
class Solution {
public:
long long ans = 0;
int ts;
int pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)
return 0;
ts = targetSum;
dfs1(root);
return ans;
}
void dfs1(TreeNode* root)
{
if(root == nullptr)
return;
dfs2(root, 0);
dfs1(root->left);
dfs1(root->right);
}
void dfs2(TreeNode* root, long long curSum)
{
if(root == nullptr)
return;
curSum += root->val;
if(curSum == ts)
ans++;
dfs2(root->left, curSum);
dfs2(root->right, curSum);
}
};
树上的前缀和:哇塞!最完整的路径是从根节点到叶子节点,这题相当于在这些路径上找区间和=targetsum的,那不就是前缀和吗!
curSum - preSum = targetSum即可。
class Solution {
public:
unordered_map preSum;
int targetSum;
int ans = 0;
int pathSum(TreeNode* root, int ts) {
if(root == nullptr)
return 0;
targetSum = ts;
preSum[0] = 1;
dfs(root, 0);
return ans;
}
void dfs(TreeNode* root, long long curSum)
{
if(root == nullptr)
return;
curSum += root->val;
if(preSum.find(curSum - targetSum) != preSum.end())
{
ans += preSum[curSum - targetSum];
}
preSum[curSum]++;
dfs(root->left, curSum);
dfs(root->right, curSum);
preSum[curSum]--;
}
};
10.14 二叉树的序列化与反序列化 lc 297
这道题主要是区分每个节点的值和null处理、负值处理的问题,其他就是递归即可
BFS
class Codec {
public:
const int nll = 2000;
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root == nullptr)
return "";
string data;
queue q;
q.push(root);
while(q.size())
{
TreeNode* tmp = q.front();
q.pop();
if(tmp == nullptr)
{
data += "_#";
continue;
}
data += "_" + to_string(tmp->val);
q.push(tmp->left);
q.push(tmp->right);
}
cout << data << endl;
return data;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data.size() == 0)
return nullptr;
vector v;
int i = 0;
while(i < data.size())
{
int j = i + 1;
while(j < data.size() && data[j] != '_')
j++;
string s = data.substr(i + 1, j - i - 1);
cout << s << endl;
if(s == "#")
v.push_back(nll);
else
v.push_back(atoi(s.c_str()));
i = j;
}
i = 0;
TreeNode* root = new TreeNode(v[i++]);
queue q;
q.push(root);
while(q.size())
{
TreeNode* tmp = q.front();
q.pop();
if(v[i] == nll)
tmp->left = nullptr;
else
{
tmp->left = new TreeNode(v[i]);
q.push(tmp->left);
}
i++;
if(v[i] == nll)
tmp->right = nullptr;
else
{
tmp->right = new TreeNode(v[i]);
q.push(tmp->right);
}
i++;
}
return root;
}
};
DFS
class Codec {
public:
const int nll = 2000;
vector v;
int i = 1;
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root == nullptr)
return "_#";
return "_" + to_string(root->val) + serialize(root->left) + serialize(root->right);
}
void helper(string data)
{
int i = 0;
while(i < data.size())
{
int j = i + 1;
while(j < data.size() && data[j] != '_')
j++;
string s = data.substr(i + 1, j - i - 1);
cout << s << endl;
if(s == "#")
v.push_back(nll);
else
v.push_back(atoi(s.c_str()));
i = j;
}
}
TreeNode* build(TreeNode* root)
{
if(v[i] == nll)
{
root->left = nullptr;
i++;
}
else
{
root->left = new TreeNode(v[i]);
i++;
build(root->left);
}
if(v[i] == nll)
{
root->right = nullptr;
i++;
}
else
{
root->right = new TreeNode(v[i]);
i++;
build(root->right);
}
return root;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if(data == "_#")
return nullptr;
helper(data);
TreeNode* root = new TreeNode(v[0]);
return build(root);
}
};
10.15 目标和 lc494
1.简单dfs
class Solution {
public:
int n;
//int ans = 0;
int findTargetSumWays(vector& nums, int target) {
n = nums.size();
return dfs(nums, target, 0, 0);
}
int dfs(vector& nums, int target, int curSum, int i)
{
if(i == n && curSum == target)
return 1;
if(i == n)
return 0;
int n1 = dfs(nums, target, curSum + nums[i], i + 1);
int n2 = dfs(nums, target, curSum - nums[i], i + 1);
return n1 + n2;
}
};
2. dfs+记忆化搜索
memo记录的是key = (i, cursum), value=要求的个数
class Solution {
public:
int n;
//int ans = 0;
unordered_map memo;
int findTargetSumWays(vector& nums, int target) {
n = nums.size();
return dfs(nums, target, 0, 0);
}
int dfs(vector& nums, int target, int curSum, int i)
{
string key = to_string(i) + "_" + to_string(curSum);
if(memo.count(key))
return memo[key];
if(i == n && curSum == target)
{
memo[key]++;
return memo[key];
}
if(i == n)
{
memo[key] = 0;
return memo[key];
}
int n1 = dfs(nums, target, curSum + nums[i], i + 1);
int n2 = dfs(nums, target, curSum - nums[i], i + 1);
memo[key] = n1 + n2;
return n1 + n2;
}
};
3. 01背包
在记忆化的基础上变成01背包
class Solution {
public:
int findTargetSumWays(vector& nums, int target) {
int n = nums.size();
int sum = 0;
for(int x: nums)
sum += x;
if(target > sum || target < -sum) return 0;
vector> dp(n + 1, vector(2 * sum + 1, 0));
dp[0][0 + sum] = 1;
for(int i = 1; i <= n; i++)
{
for(int cur = -sum; cur <= sum; cur++)
{
if(cur - nums[i - 1] >= -sum)
dp[i][cur + sum] = dp[i - 1][cur - nums[i - 1] + sum];
if(cur + nums[i - 1] <= sum)
dp[i][cur + sum] += dp[i - 1][cur + nums[i - 1] + sum];
}
}
return dp[n][target + sum];
}
};
10.15 分割等和子集 lc 416
划分两个子集使得x = y,也即是找到一个子集使得x=sum/2。也就是从这些数字中选一些数使得和为sum/2。
01背包问题
class Solution {
public:
int n;
bool canPartition(vector& nums) {
n = nums.size();
int sum = 0;
for(int x: nums)
sum += x;
if(sum % 2) return false;
else return findTargetSumWays(nums, sum / 2);
}
int findTargetSumWays(vector& nums, int target)
{
vector> dp(n + 1, vector(target + 1, false));
for(int i = 0; i <= n; i++)
dp[i][0] = true;
for(int i = 1; i <= n; i++)
{
for(int cur = 0; cur <= target; cur++)
{
dp[i][cur] = dp[i - 1][cur];
if(nums[i - 1] <= cur)
dp[i][cur] = dp[i][cur] || dp[i - 1][cur - nums[i - 1]];
}
}
return dp[n][target];
}
};
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-21dgU3as-1668235849934)(10_leetcode.assets/image-20221027170532069.png)]
!10.15 用栈操作构建数组 lc 1441
!10.16 可能的二分法 lc 886
10.17 完全平方数
还是01背包问题,就是从平方和中选选到和为target的最小数量
class Solution {
public:
const int INF = 0x3f3f3f3f;
int numSquares(int n) {
vector sq;
for(int i = 0; i * i <= n; i++)
sq.push_back(i * i);
int dp[n + 1];
memset(dp, INF, sizeof dp);
dp[1] = 1;
dp[0] = 0;
for(int i = 0; i < sq.size(); i++)
{
for(int j = 0; j <= n; j++)
{
if(sq[i] <= j)
dp[j] = min(dp[j], dp[j - sq[i]] + 1);
}
}
return dp[n];
}
};
10.17 零钱兑换 lc 322
完全背包问题:物品可以无限使用,要求背包装满,要求使用的数量最少。
在满足:amount=v1x1+v2x2+v3x3+…+vnxn 的条件下,求: target=min{x1+x2+x3+…xn}可以dfs将所有的组合拿出来,然后取硬币数最小。
dp[i]表示硬币和为i时的最小硬币数,然后看取不取前i个硬币,取最小即可。
class Solution {
public:
const int INF = 0x3f3f3f3f;
int coinChange(vector& coins, int amount) {
int n = coins.size();
int dp[amount + 1];
memset(dp, INF, sizeof dp);
dp[0] = 0;
for(int i = 0; i < n; i++)
{
for(int j = 0; j <= amount; j++)
{
if(coins[i] <= j)
{
dp[j] = min(dp[j], dp[j - coins[i]] + 1);
}
}
}
if(dp[amount] == INF)
return -1;
else
return dp[amount];
}
};
!10.17 水果成篮 lc 904
!10.18 最大为 N 的数字组合 lc 902
10.18 环形链表 lc 141
快慢指针
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head == nullptr)
return false;
if(head->next == nullptr)
return false;
ListNode* fast = head;
ListNode* slow = head;
while(fast != nullptr)
{
slow = slow->next;
fast = fast->next;
if(fast != nullptr)
fast = fast->next;
if(slow == fast)
return true;
}
return false;
}
};
10.18 环形链表|| lc 142
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* fast = head, *slow = head;
if(head == nullptr) return nullptr;
if(head->next == nullptr) return nullptr;
while(fast != nullptr)
{
slow = slow->next;
fast = fast->next;
if(fast != nullptr)
fast = fast->next;
if(fast == slow)
{
fast = head;
while(fast != slow)
{
fast = fast->next;
slow = slow->next;
}
return fast;
}
}
return nullptr;
}
};
10.18 删除链表的倒数第 N 个结点 lc 19
还是快慢指针找到倒数第n个节点然后再删除~下次再练习
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* p = head;
if(head->next == nullptr)
return nullptr;
for(int i = 0; i < n; i++)
p = p->next;
ListNode* q = head;
if(p == nullptr)
return head->next; //删掉头节点
while(p->next != nullptr)
{
p = p->next;
q = q->next;
}
ListNode* nx = q->next;
q->next = nx->next;
return head;
}
};
10.19 无法吃午餐肉的同学 lc 1700
模拟
class Solution {
public:
int countStudents(vector& students, vector& sandwiches) {
int n = students.size();
int s0 = 0, s1 = 0;
for(int x: students)
{
if(x) s1++;
else s0++;
}
for(int x: sandwiches)
{
if(x == 1 && s1 > 0) s1--;
else if(x == 0 && s0 > 0) s0--;
else break;
}
return s0 + s1;
}
};
10.19 括号的生成 lc 22
回溯
class Solution {
public:
//主要是保证右括号不能在左括号之前生成
vector ans;
string tmp;
vector generateParenthesis(int n) {
dfs(n, n, tmp);
return ans;
}
void dfs(int left, int right, string tmp)
{
if(left == 0 && right == 0)
{
ans.push_back(tmp);
tmp = "";
return;
}
if(left > 0)
dfs(left - 1, right, tmp +'(');
if(right > left)
dfs(left, right - 1, tmp +')');
}
};
10.19 组合总和 lc 39
回溯
class Solution {
public:
vector> ans;
vector tmp;
vector> combinationSum(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
dfs(candidates, target, 0, 0);
return ans;
}
void dfs(vector& candidates, int target, int curSum, int i)
{
if(curSum == target)
{
ans.push_back(tmp);
return;
}
if(curSum > target)
{
return;
}
for(int j = i; j < candidates.size(); j++)
{
tmp.push_back(candidates[j]);
dfs(candidates, target, curSum + candidates[j], j);
tmp.pop_back();
}
}
};
10.19 组合总数 II lc 40
class Solution {
public:
vector> ans;
vector tmp;
vector> combinationSum2(vector& candidates, int target) {
sort(candidates.begin(), candidates.end());
dfs(candidates, target, 0, 0);
return ans;
}
void dfs(vector& candidates, int target, int cur, int last)
{
if(cur == target)
{
ans.push_back(tmp);
return;
}
if(cur > target)
{
return;
}
for(int i = last; i < candidates.size(); i++)
{
if(i > last && candidates[i] == candidates[i - 1])
continue;
tmp.push_back(candidates[i]);
dfs(candidates, target, cur + candidates[i], i + 1);
tmp.pop_back();
}
}
};
10.19 电话号码的字母组合 lc 17
回溯
class Solution {
public:
unordered_map map;
vector ans;
int n;
string tmp;
vector letterCombinations(string digits) {
n = digits.size();
if(n == 0) return {};
map['2'] = "abc";
map['3'] = "def";
map['4'] = "ghi";
map['5'] = "jkl";
map['6'] = "mno";
map['7'] = "pqrs";
map['8'] = "tuv";
map['9'] = "wxyz";
dfs(digits, 0, tmp);
return ans;
}
void dfs(string digits, int i, string tmp)
{
if(tmp.size() == n)
{
ans.push_back(tmp);
tmp = "";
return;
}
int s = digits[i];
for(int j = 0; j < map[s].size(); j++)
{
char ch = map[s][j];
dfs(digits, i + 1, tmp + ch);
}
}
};
10.20 缺失的第一个正数 lc 41
最大的缺失的正数也不会超过nums.size()。还是和下标相关
把每个数放在下标应该在的数上,然后从0开始判断如果和下标不一样的第一个数就是缺失的第一个正数。
class Solution {
public:
int firstMissingPositive(vector& nums) {
int n = nums.size();
for(int i = 0; i < n; i++)
{
while(nums[i] > 0 && nums[i] < n && nums[i] != nums[nums[i] - 1])
swap(nums[i], nums[nums[i] - 1]);
}
for(int i = 0; i < n; i++)
{
if(nums[i] != i + 1)
return i + 1;
}
return n + 1;
}
};
10.20 寻找重复数 lc 287
把数组看成链表,找到环的入口
class Solution {
public:
int findDuplicate(vector& nums) {
//将数组看成链表,找到环的入口
int slow = 0, fast = 0;
while(1)
{
slow = nums[slow];
fast = nums[nums[fast]];
if(slow == fast)
break;
}
fast = 0;
while(slow != fast)
{
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
10.20 找到所有数组中消失的数字 lc 448
就是把出现的数字和下标关联起来,将出现的数字的下标存储的数变成负数,最后是正数的就是缺失的。
class Solution {
public:
vector findDisappearedNumbers(vector& nums) {
vector ans;
for(int i = 0; i < nums.size(); i++)
{
nums[abs(nums[i]) - 1] = - abs(nums[abs(nums[i]) - 1]);
}
for(int i = 0; i < nums.size(); i++)
{
if(nums[i] > 0)
ans.push_back(i + 1);
}
return ans;
}
};
10.20 第K个语法符号lc 779
class Solution {
public:
int kthGrammar(int n, int k) {
if(n == 1)
return 0;
return !(k % 2)^kthGrammar(n - 1, (k + 1) / 2);
}
};
10.21 股票价格跨度 lc 901
单调栈:单调递减栈,当出现新价格大于栈顶价格时,就需要pop找出栈里面所有小于的,保持单调递减
class StockSpanner {
public:
stack stk;
vector v;
int idx = 0;
StockSpanner() {
idx++;
v.push_back(INT_MAX);
stk.push(0);
}
int next(int price) {
v.push_back(price);
while(stk.size() && v[stk.top()] <= price) {
stk.pop();
}
int i = stk.top();
stk.push(idx);
return idx++ - i;
}
};
10.22 根据身高重建队列 lc 406
按照身高从大到小排序,如果身高相同先排k小的。然后一个个插入,如果现有元素数量大于k的要求了,说明前面高个的太多了,需要把当前元素往前排。如果小于k的要求则直接插入即可,后面会随着插入而满足条件的。
struct peo
{
int h, k;
};
bool cmp(const peo& p1, const peo& p2)
{
if(p1.h != p2.h)
return p1.h > p2.h;
else return p1.k < p2.k;
}
class Solution {
public:
vector> reconstructQueue(vector>& people) {
int n = people.size();
peo P[n];
for(int i = 0; i < n; i++)
{
P[i].h = people[i][0];
P[i].k = people[i][1];
}
sort(P, P + n, cmp);
vector> ans;
for(int i = 0; i < n; i++)
{
if(ans.size() <= P[i].k)
ans.push_back({P[i].h, P[i].k});
else
ans.insert(ans.begin() + P[i].k, {P[i].h, P[i].k});
return ans;
}
};
10.22 规划兼职工作lc 1235
按照endtime排序,然后dp[i]表示使用前i个元素的获得的最大报酬。
struct job {
int s, e, p;
};
bool cmp(const job& j1, const job& j2) {
return j1.e < j2.e;
}
class Solution {
public:
int jobScheduling(vector& startTime, vector& endTime, vector& profit) {
int n = startTime.size();
job jobs[n];
for(int i = 0; i < n; i++) {
jobs[i].s = startTime[i];
jobs[i].e = endTime[i];
jobs[i].p = profit[i];
}
sort(jobs, jobs + n, cmp);
int dp[n];
dp[0] = jobs[0].p;
for(int i = 1; i < n; i++) {
dp[i] = max(dp[i - 1], jobs[i].p);
for(int j = i - 1; j >= 0; j--) {
if(jobs[j].e <= jobs[i].s) {
dp[i] = max(dp[i], dp[j] + jobs[i].p);
break;
}
}
}
return dp[n - 1];
}
};
10.24 除自身以外的乘积 lc 238
剑指offer中的一道题,前缀统计nums[i]左侧的,后缀统计nums[i]右侧的,一共O(n)
class Solution {
public:
vector productExceptSelf(vector& nums) {
int n = nums.size();
vector ans(n, 1);
int pre = 1, suf = 1;
for(int i = 0; i < n; i++) {
ans[i] *= pre;
pre *= nums[i];
}
for(int i = n - 1; i >= 0; i--) {
ans[i] *= suf;
suf *= nums[i];
}
return ans;
}
};
10.24 和为k的子数组 lc 560
前缀和+哈希表
class Solution {
public:
int subarraySum(vector& nums, int k) {
unordered_map hmap;
hmap[0] = 1;
int sum = 0, ans = 0;
for(int i = 0; i < nums.size(); i++) {
sum += nums[i];
if(hmap.count(sum - k)) {
ans += hmap[sum - k];
}
hmap[sum]++;
}
return ans;
}
};
10.24 分割数组 lc 915
只要左边的max <= 右边的min即可, O(n)的
右边的min可以先统计以下,最后加上一个INT_MAX哨兵
class Solution {
public:
int partitionDisjoint(vector& nums) {
int mi = INT_MAX, ma = 0;
vector minNums(nums.size(), INT_MAX);
for(int i = nums.size() - 1; i >= 0; i--) {
mi = min(mi, nums[i]);
minNums[i] = mi;
}
minNums.push_back(INT_MAX);
for(int i = 0; i < nums.size(); i++) {
ma = max(ma, nums[i]);
if(ma <= minNums[i + 1]) {
return i + 1;
}
}
return 0;
}
};
10.25 最短的桥 934
10.26 任务调度器 lc 621
class Solution {
public:
int leastInterval(vector& tasks, int n) {
int cnt[26];
int max_cnt = 0, max_cnt_same = 0;
memset(cnt, 0, sizeof cnt);
for(int i = 0; i < tasks.size(); i++) {
cnt[tasks[i] - 'A']++;
}
for(int i = 0; i < 26; i++) {
max_cnt = max(max_cnt, cnt[i]);
}
for(int i = 0; i < 26; i++) {
if(max_cnt == cnt[i]) {
max_cnt_same++;
}
}
int ans = (n + 1) * (max_cnt - 1) + max_cnt_same;
//而当任务数超过该值时,我们可以在将其横向添加每个n+1 块的后面,同时不会引入额外的冻结时间
return max(ans, tasks.size());
}
};
10.26 和至少为k的最短子数组 lc 862
暴力解法(超时):按照len遍历+滑动窗口, O ( n 2 ) O(n ^2) O(n2)的复杂度(注意:所有sum小于k不一定代表里面没有大于等于k的子数组,因为有负数的存在)。
class Solution {
public:
int shortestSubarray(vector& nums, int k) {
int n = nums.size();
for(int len = 1; len <= n; len++) {
int s = accumulate(nums.begin(), nums.begin() + len, 0);
if(s >= k) return len;
for(int l = 1; l + len - 1 < n; l++) {
int r = l + len - 1;
s = s + nums[r] - nums[l - 1];
if(s >= k) return len;
}
}
return -1;
}
};
10.28 戳气球 lc 312
很难的区间dp
class Solution {
public:
int maxCoins(vector& nums) {
int n = nums.size();
nums.push_back(1);
nums.insert(nums.begin(), 1);
int dp[n + 2][n + 2];
memset(dp, 0, sizeof dp);
//全都戳破的上一个状态是只剩一个没被戳破
//dp[l][r]不包含l, r中k表示最后戳破的气球,最后就剩下 l, k, r了
for(int len = 3; len <= n + 2; len++) {
for(int l = 0; l + len - 1 <= n + 1; l++) {
int r = l + len - 1;
for(int k = l + 1; k <= r - 1; k++) {
dp[l][r] = max(dp[l][r], dp[l][k] + dp[k][r] + nums[l] * nums[k] * nums[r]);
}
}
}
return dp[0][n + 1];
}
};
10.28 子数组的最小值之和 lc 907
单调栈的应用题:计算每个值作为子数组最小值的次数,就需要分别向左向右找第一个小于arr[i]的值,假设最远子数组为(l, r),依据乘法原理子数组的个数就是(i - l) * (r - i)
还有很重要的一点就是:可能有重复的!
比如[1, 2, 3, 2, 3, 1]两个2计算的最远子数组都是(0, 5),那么就会在[1, 4]这个区间内重复计算两个2的子数组个数
我们需要向左找第一个小于的,向右找第一个小于等于的,那么这样左边的2最远子数组就是(0, 3),右边的就是(0, 5),这样就不会重复计算了!
class Solution {
public:
const int mod = 1e9 + 7;
int sumSubarrayMins(vector& arr) {
int n = arr.size();
//加俩哨兵
arr.push_back(0);
arr.insert(arr.begin(), 0);
int ans = 0;
stack stk;
stack stk1;
int left[n + 2];
int right[n + 2];
stk.push(0);
for(int i = 1; i <= n; i++) {
while(!stk.empty() && arr[stk.top()] >= arr[i]) {
stk.pop();
}
left[i] = i - stk.top();
//cout << i << " " << left[i] << endl;
stk.push(i);
}
stk1.push(n + 1);
for(int i = n; i > 0; i--) {
while(!stk1.empty() && arr[stk1.top()] > arr[i]) {
stk1.pop();
}
right[i] = stk1.top() - i;
stk1.push(i);
}
for(int i = 1; i <= n; i++) {
ans = (ans + (long long)left[i] * right[i] * arr[i]) % mod;
}
return ans;
}
};
10.30 LRU缓存 lc 146
哈希表+ 双向链表:最关键的就是加上一个头节点和尾节点,剩下的就仔细写仔细调试就可以了。
struct Node
{
int key;
int value;
Node* next;
Node* pre;
Node(int k, int v)
{
key = k;
value = v;
next = nullptr;
pre = nullptr;
}
};
class LRUCache {
public:
Node* head;
Node* nail;
int cnt = 0;
int cap;
unordered_map hashmap;
LRUCache(int capacity) {
cap = capacity;
head = new Node(-1, -1);
nail = new Node(-1, -1);
head->next = nail;
head->pre = nail;
nail->next = head;
nail->pre = head;
}
int get(int key) {
if(hashmap.find(key) == hashmap.end())
return -1;
Node* tmp = hashmap[key];
remove(tmp);
addFromHead(tmp);
return tmp->value;
}
void remove(Node* t)
{
hashmap.erase(t->key);
Node* pt = t->pre;
Node* nt = t->next;
pt->next = nt;
nt->pre = pt;
cnt--;
}
void addFromHead(Node* t)
{
hashmap[t->key] = t;
Node* nt = head->next;
t->next = nt;
t->pre = head;
head->next = t;
nt->pre = t;
cnt++;
}
void put(int key, int value) {
if(get(key) != -1)
{
head->next->value = value;
return;
}
if(cnt < cap)
{
Node* tmp = new Node(key, value);
addFromHead(tmp);
}
else
{
Node* tmp = new Node(key, value);
Node* nt = nail->pre;
remove(nt);
addFromHead(tmp);
}
}
};
10.30 字母大小写全排列 lc 784
回溯
class Solution {
public:
vector ans;
string tmp;
vector letterCasePermutation(string s) {
dfs(s, 0);
return ans;
}
void dfs(string s, int i)
{
if(i == s.size())
{
ans.push_back(tmp);
return;
}
if(s[i] >= '0' && s[i] <= '9')
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
}
else if(s[i] >= 'a' && s[i] <= 'z')
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
tmp += (s[i] - 32);
dfs(s, i + 1);
tmp.pop_back();
}
else
{
tmp += s[i];
dfs(s, i + 1);
tmp.pop_back();
tmp += (s[i] + 32);
dfs(s, i + 1);
tmp.pop_back();
}
}
};
10.30 最小栈 lc 155
两个栈辅助的
class MinStack {
public:
stack stk;
stack minstack;
MinStack() {
}
void push(int val) {
stk.push(val);
if(minstack.empty() || val <= minstack.top())
minstack.push(val);
}
void pop() {
int x = stk.top();
cout << x << endl;
stk.pop();
if(minstack.size() && x == minstack.top())
minstack.pop();
}
int top() {
return stk.top();
}
int getMin() {
cout << minstack.top() << endl;
return minstack.top();
}
};
链表解决的:头插法,每个节点中记录栈顶当前值和当前值作为栈顶时的最小值。
struct node
{
int val;
int min;
node* next;
node(int x, int y)
{
val = x;
min = y;
next = nullptr;
}
};
class MinStack {
public:
node* head;
MinStack() {
head = nullptr;
}
void push(int val) {
if(head == nullptr)
head = new node(val, val);
else
{
int m = val <= head->min? val: head->min;
node* tmp = new node(val, m);
tmp->next = head;
head = tmp;
}
}
void pop() {
head = head->next;
}
int top() {
return head->val;
}
int getMin() {
return head->min;
}
};
10.31 滑动窗口的最大值 lc 239
模拟滑动窗口不行因为如果排出最大值要重新遍历找最大值,会超时
因此,选择双向队列维护一个单调递减的队列,当删掉的值==左边最大值时,将其删掉.当加入的值大于队尾的值时,删掉队尾维持递减队列.
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
vector ans;
int n = nums.size();
deque q;
int l = 0, r = k - 1;
for(int i = l; i <= r; i++)
{
while(q.size() && nums[i] > q.back())
q.pop_back();
if(!q.size() || nums[i] <= q.back())
q.push_back(nums[i]);
}
ans.push_back(q.front());
while(r + 1 < n)
{
if(q.size() && nums[l] == q.front())
q.pop_front();
while(q.size() && nums[r + 1] > q.back())
q.pop_back();
q.push_back(nums[r + 1]);
ans.push_back(q.front());
l++;
r++;
}
return ans;
}
};
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
deque q;
vector ans;
for(int i = 0; i < nums.size(); i++) {
if(!q.empty() && i >= k && nums[i - k] == q.front()) {
q.pop_front();
}
while(!q.empty() && nums[i] > q.back()) {
q.pop_back();
}
q.push_back(nums[i]);
if(i >= k - 1) {
ans.push_back(q.front());
}
}
return ans;
}
};
10.31 神奇字符串 lc481
模拟题目即可,小技巧 1^3 = 2 2^3 = 1
class Solution {
public:
int magicalString(int n) {
int x1 = 3, x2 = 3; //x1是总的字符串数量,x2是生成到哪一个
vector s(4, 0);
s[1] = 1; s[2] = 2; s[3] = 2;
int cnt = 1, f = 1;;
while(x1 < n)
{
int t = 0;
if(s[x2] == 1)
{
s.push_back(f);
cnt += (f == 1);
x1++;
}
else
{
s.push_back(f);
s.push_back(f);
x1 += 2;
cnt += (f == 1) * 2;
}
f = f ^ 3;
x2++;
}
if(x1 > n && s[x1] == 1) cnt--;
return cnt;
}
};
10.31 课程表 lc 207
气死我了,一个拓扑排序写了这么久…
const int N = 5010;
int h[N], e[N], ne[N], idx;
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
class Solution {
public:
bool canFinish(int numCourses, vector>& prerequisites) {
idx = 0;
int inorder[numCourses];
queue q;
memset(h, -1, sizeof h);
memset(inorder, 0, sizeof inorder);
for(int i = 0; i < prerequisites.size(); i++) {
add(prerequisites[i][1], prerequisites[i][0]);
inorder[prerequisites[i][0]]++;
}
for(int i = 0; i < numCourses; i++) {
if(inorder[i] == 0) {
q.push(i);
inorder[i] = -1;
}
}
int cnt = 0;
while(!q.empty()) {
int t = q.front();
q.pop();
cnt++;
for(int i = h[t]; i != -1; i = ne[i]) {
int b = e[i];
inorder[b]--;
if(!inorder[b]) {
q.push(b);
}
}
}
return cnt == numCourses;
}
};
一些有的没的
-
字符串转int atoi()但是还需要从string 转到char : s.c_str()
即 int x = atoi(s.c_str());
int转string : string s = to_string(x);
- priority_queue