Dijkstra算法、A*、JPS算法原理和代码

本文介绍基于搜索的路径规划算法：Dijkstra算法、A*、JPS算法原理，同时讲解Dijkstra算法和A*算法的代码（C++）

1.Dijkstra算法原理

Dijkstra算法的基础是广度优先搜索算法，例如在一个栅格地图中寻找从起点（也就是五角星的位置）到终点（紫色的×的位置）最优路径，Dijkstra算法会向洪水一样一直往外扩散，寻找终点，直到新扩展到的节点包含了终点，就会停止搜索，找到了一条最优路径，基本流程如下：

（1）创建优先级队列来存储所有需要扩展的节点；
（2）优先级队列初始化时加入初始节点，也就是起点；
（3）假设除了起始节点外的所有节点的成本函数（当前扩展的节点到起点的成本）为无穷大；
（4）进行循环：
（4.1）如果优先级队列为空，就跳出循环；
（4.2）从优先级队列中移除具有最低成本函数的节点，同时把该节点标记为已经扩展过；
（4.3）判断该节点是不是终点，如果是的话，跳出循环；
（4.4）对于所有未扩展的节点：4.4.1） 如果成本函数为无穷，就更新当前节点的成本函数等于上一个节点的成本函数加上一个节点到当前节点的成本 g(m) = g(n) +Cnm；4.4.2）把该节点放入优先级队列中；4.4.3）如果当前节点的成本函数大于上一个节点的成本函数加上一个节点到当前节点的成本；就把当前节点的成本函数更新为上一个节点的成本函数加上一个节点到当前节点的成本 g(m) = g(n) + Cnm ；

2.A*算法

2.1 A*算法原理

A*算法是Dijkstra算法的改进，因此和Dijkstra算法的原理相近，有细微区别,下面来讲Astar算法的原理：

A* 算法的提出是为了解决Dijkstra算法在搜索最优路径的时候扩展了扩展了太多节点，搜索效率不高的问题，A* 算法相对于Dijkstra算法最核心的改进是加入了启发函数，启发函数估计了要扩展的节点离终点的距离，这样使得搜索最优路径的时候目的性更强，朝着离终点更近的节点扩展搜索更高效；
这里不再赘述，因为A*算法只有最终的成本函数加了一项h(n),从Dijkstra算法的成本函数g(n)变成了现在的g(n) + h(n)如果h(n)=0的话，那么就是Dijkstra算法；

2.2 加权A*算法

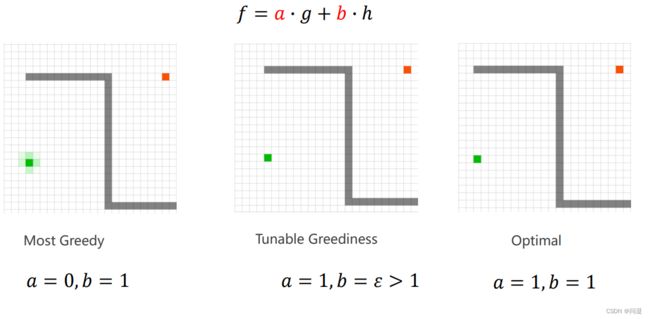
加权A* 算法是对A* 算法的改进，在代价函数g和启发函数h前面增加了系数，当a=0时，就变成了贪心算法；当a=1，b>1时，A* 算法此时搜索终点的速度相比A* 算法更快，但是不能保证搜索的路径为最优路径；当a=1，b=0时，就是Dijkstra算法。

2.3 提升A*算法搜索速度的技巧

2.3.1 启发函数的选择

启发函数的选择对于A* 算法搜索路径的速度十分重要，好的启发函数能快速搜索出最优路径，而选择的错误可能会使A* 算法花费时间长，同时搜索出的还不是最优路径；下面来说一说A* 算法启发函数的选择问题：
常用的启发函数有L1范数、L2范数、L∞范数以及启发函数为0，在选择启发函数之前，首先需要说一下保证搜索出最优路径的启发函数的选择要求：启发函数计算的到终点的距离必须比真实的距离小，否则搜索出的就有可能不是最优路径。
那知道了原则之后，具体问题具体分析，只要比到终点的真实距离小就可以搜索出最优路径了，但是我这里想介绍一个启发函数，一般情况下比上面介绍的几个启发函数更优，给大家解释一下这个启发函数怎么理解。

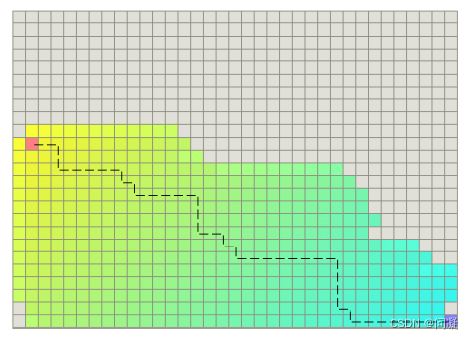
这个启发函数就是先计算水平和垂直方向的距离，然后如果我们可以沿着对角走的话，那么比较水平和垂直距离哪个大，大的那个沿着栅格走，因为这一段沿着栅格走距离比沿着对角走短，而距离小的那个沿着对角走是因为如果不沿着对角走的话那么就要沿着栅格走两步，如上图所示，大家可以看看黄色的路径是不是最优的。

2.3.2 Tie breaker

A* 算法之所以可以加技巧提升搜索速度是因为在搜索过程中如果有很多节点的f值相同，那么就会扩展这些节点，Tie breaker技巧的思想就是打破对称性，让之前相同f值的节点，f值都有一些细微不同，那么f值的大小不同，就不会同时扩展这些节点了，从而提升了搜索的速度。

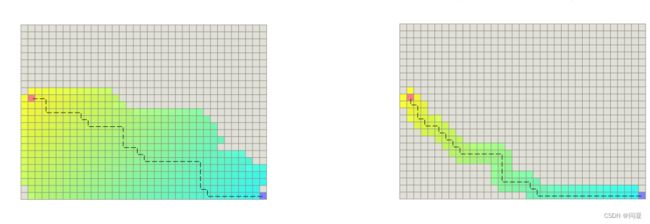
Tie breaker的技巧公式如图所示，给启发函数h乘以一个值p，p一般都很小，可以给0.001-0.005之间，因为f值相同有可能是3+1=0.5+3.5这种情况，那么启发函数放大了一点点之后，显然两个节点的f值就不相同了，从而打破了对称性。可以看下图，左边是没有用Tie breaker技巧搜索最优路径扩展过的节点，右边的是加入Tie breaker之后的，扩展的节点明显少了很多，那么速度也自然会提升。

3.JPS算法

3.1JPS算法原理

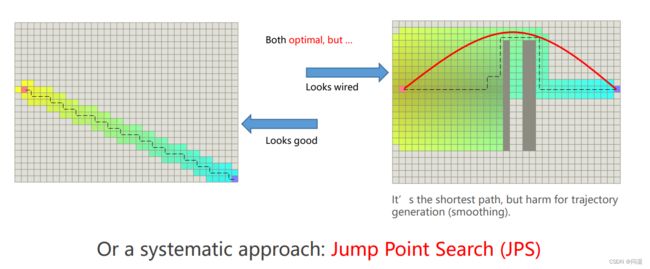
介绍跳点寻路算法之前，我们先来说一下，为何会出现这种算法，A* 算法虽然能搜索出最优路径，但是最优路径比较反直觉，不符合驾驶员开车的习惯，虽然对规划出的路径进行优化可以缓解，但是规划处的路径太反直觉的话优化轨迹也好不了多少，因此需要搜索出的路径符合驾驶员的习惯一些，符合直觉一点。下图可以看到了有图虚线的最优路径，开车先离障碍物很近再去绕开它是不是就很反直觉呢？而红色的较优轨迹是不是很难从虚线优化出来呢，或者说几乎不可能。明白了这一点之后我们来介绍JPS算法。

那么我们来说一下JPS算法的原理，其实JPS算法就是改进的A* 算法，区别是JPS算法寻找邻居的方式和A*算法不同，我们来讲一下JPS算法向前跳跃的规则：假设当前处在x节点，如果能够通过x的父节点到达x要扩展的节点并且路径的代价小于或者等于x节点到达该节点的代价，那么就不需要通过x节点到达该节点，也就是x就不需要扩展该节点了。
首先看下图左边没有黑色方框的两个正方形，看一下节点2，节点2通过x到达的话，那么从4到2的代价为2，但是通过4直接到达代价为根号2，所以比通过x到达代价小，那么x节点就不需要扩展2节点了；同理，来看一下节点3，节点3通过x到达的代价为根号2+1，直接从节点4到达的代价也是根号2+1，两者相等同样没必要通过x扩展节点3；7、8节点同理；因为2、3、7、8通过x的父节点到达代价小于或者等于通过x到达的代价，所以就不需要扩展这些节点了。
其次我们来看一看强迫邻居这个概念，看右边这两幅带有黑色方块的图：先看这两个中的第一个图，在上面讲的呢，我们不需要扩展节点3，因为通过x的父节点可以到达，但是现在节点4直接到达的路走不通，那么我们就只能扩展节点3了，3就称为x的强迫邻居也就是Forced Neighbors；第二幅图也是同样的道理，因为节点6到达节点1的路走不通，只能通过节点x扩展，所以节点1被称为x的Forced Neighbors。
知道了JPS算法怎么跳跃以及Look ahead的规则、Forced Neighbors的概念之后，我们来以一个例子解释JPS算法搜索的过程：

第一步，在起始点开始搜索的时候，把起点加入open list中，JPS算法会水平、垂直、对角线搜索，如果水平碰到障碍物就说明此路不通，然后垂直搜索还遇到障碍物的话，就对角搜索；
第二步，当前搜索结束需要找到了一个Forced Neighbors，然后把起点移出open list中，把具有Forced Neighbors的节点的上一个节点也就是它的父节点（一个关键节点）加入open list中，然后从该节点开始继续往下搜索；
第三步，移出Forced Neighbors的节点的父节点，把具有Forced Neighbors的节点加入open list中，也就是黑色长条上面的那个灰色方块，它继续搜索，水平搜索和垂直搜索都碰到了障碍物，那就开始对角搜索；对角线方向移动两步之后，垂直搜索就找到了终点，找到终点也就是找到了一个关键节点，具有Forced Neighbors的节点移出open list，那就把终点的上一个节点加入open list。
第四步，JPS算法的路径就由若干个关键节点组成，JPS算法就找了一条合适的路径，前面忘记说了这里补充一下，关键节点移出open list之后就会加入closed list。

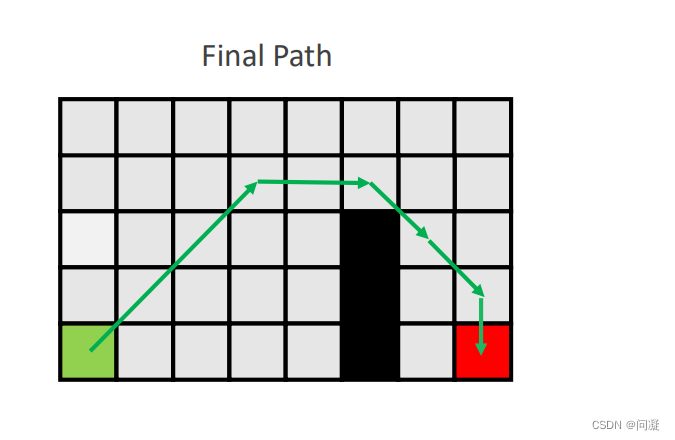
3.2JPS算法总结

1.JPS算法在大部分情况下比A* 算法的搜素路径的速度更快；
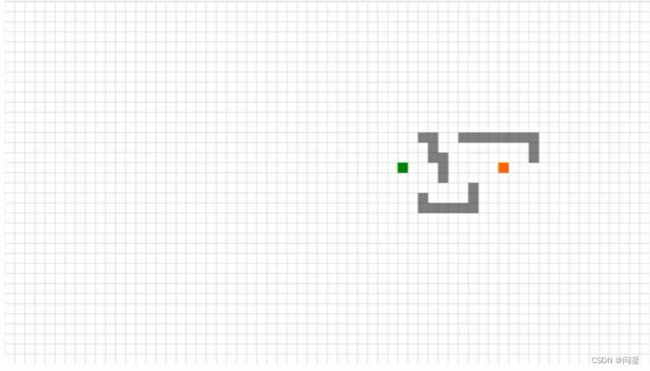
2.JPS算法的不足在于会增加对环境障碍物碰撞的查询，因此在空旷地方很多的地方，会浪费很多时间，这种情况下效果甚至不如A*算法，如下图所示，在下图的情况中，JPS算法在起点（绿色的点）搜索开始的时候，会水平和垂直的搜索直到遇到障碍物，然后开始对角搜，那么可以看到这个栅格地图左边空旷的部分很大，JPS算法第一步的水平和垂直搜索会扩展很多的无用的节点，这种情况下JPS算法搜索的速度就十分的慢；JPS算法的局限性还在于它只适用于栅格地图上，对于广义的图搜索问题，JPS算法不适用。

Notes: 讲完了Dijsktra算法、A*算法的原理、启发函数的选择以及小技巧和JPS算法，下面我们来讲一讲代码吧。只了解代码的原理是远远不够的，只有编写代码才能理解算法的精髓，下面来具体讲一讲Dijkstra算法和Astar算法代码；因为 A * 算法的h(n)=0时,Astar算法就是Dijkstra算法，那我就仔细讲一讲Astar算法的代码，Dijkstra算法只需要让启发函数h(n)=0即可，就不再赘述。

4.A*算法代码

这里只对核心部分的代码做讲解，具体可运行的工程项目代码可以去Github战即可，这里讲的不是可运行的完整的代码！！！

4.1 编写启发函数h(n)的代码

double AstarPathFinder::getHeu(GridNodePtr node1, GridNodePtr node2)
{
    /* 
    choose possible heuristic function you want
    Manhattan, Euclidean, Diagonal, or 0 (Dijkstra)
    */
    Eigen::Vector3d node1_coordinate = node1->coord;
    Eigen::Vector3d node2_coordinate = node2->coord;

    double dx = node1_coordinate[0] - node2_coordinate[0];
    double dy = node2_coordinate[1] - node2_coordinate[1];
    double dz = node1_coordinate[2] - node2_coordinate[2];

    double D1 = 1;
    double D2 = sqrt(2);
    double D3 = sqrt(3);

    double Diagonal_min = min(min(dx, dy), dz);
    double Diagonal_max = max(max(dx, dy), dz)
    double Diagonla_mid = dx + dy + dz - Diagonal_max - Diagonal_min;

    double heuristic_distance_ = (D3 - D2) * Diagonal_min + (D2 - D1) * Diagonla_mid + D1 * Diagonal_max;  // Diagonal heuristic function

    return heuristic_distance_;
}

这里写的代码就是计算启发函数的代码，代码比较好理解，首先得到了当前节点node1和终点node2的坐标，然后选择对角启发函数计算两点之间的距离即可，也可以用曼哈顿距离、欧几里得距离、或者L0以及L∞范数均可，自己选择即可。

4.2 准备工作

void AstarPathFinder::AstarGraphSearch(Vector3d start_pt, Vector3d end_pt)
{   
    ros::Time time_1 = ros::Time::now();    

    //index of start_point and end_point
    Vector3i start_idx = coord2gridIndex(start_pt);
    Vector3i end_idx   = coord2gridIndex(end_pt);
    goalIdx = end_idx;

    //position of start_point and end_point
    start_pt = gridIndex2coord(start_idx);
    end_pt   = gridIndex2coord(end_idx);

    //Initialize the pointers of struct GridNode which represent start node and goal node
    GridNodePtr startPtr = new GridNode(start_idx, start_pt);
    GridNodePtr endPtr   = new GridNode(end_idx,   end_pt);

    //openSet is the open_list implemented through multimap in STL library
    openSet.clear();
    // currentPtr represents the node with lowest f(n) in the open_list
    GridNodePtr currentPtr  = NULL;
    GridNodePtr neighborPtr = NULL;

    //put start node in open set
    startPtr -> gScore = 0;
    startPtr -> fScore = getHeu(startPtr,endPtr);   
    //STEP 1: finish the AstarPathFinder::getHeu , which is the heuristic function
    startPtr -> id = 1; 
    startPtr -> coord = start_pt;
    openSet.insert( make_pair(startPtr -> fScore, startPtr) );
  

    GrdiNodeMap[start_idx[0]][start_idx[1]][start_idx[2]]->id == 1;  // 将加入open list的节点做标记，方便后面回溯找路径
    vector<GridNodePtr> neighborPtrSets;
    vector<double> edgeCostSets;

讲一下上面的代码，首先传入的是两个点的坐标，找到这两个点的在GridNodeMap上的索引，并找到两个点的坐标，定义两个GridNodePtr类型的指针；
把起点放入优先级队列中，优先级队列用的是C++的multimap实现的，把startPtr的f(n)值初始化为距离终点的距离，g(n)值初始化为0；
同时把起点在GridNodeMap中的id标记为1，表示已经加入open list中；

4.3把具有最低f(n)值的节点移除open list，加入close list

 while ( !openSet.empty() ){
       
        currentPtr = openSet.begin()->second;
        openSet.erase(openSet.begin());
        Eigen::Vector3i current_idx = currentPtr->index;
        GridNodeMap[current_idx[0]][current_idx[1]][current_idx[2]]->id = -1; // 将已经访问过的节点标记，加入closed list

        // if the current node is the goal 
        if( currentPtr->index == goalIdx ){
            ros::Time time_2 = ros::Time::now();
            terminatePtr = currentPtr;
            ROS_WARN("[A*]{sucess}  Time in A*  is %f ms, path cost if %f m", (time_2 - time_1).toSec() * 1000.0, currentPtr->gScore * resolution );            
            return;
            //get the succetion
        AstarGetSucc(currentPtr, neighborPtrSets, edgeCostSets); 
        }

因为openList是有序的，所以begin位置的节点具有最低f(n)值，因此将该节点移除open list，加入close list，加入close list的操作和open list类似，只需把GridNodeMap中的id标记为-1即可。

4.4扩展节点加入open list

inline void AstarPathFinder::AstarGetSucc(GridNodePtr currentPtr, vector<GridNodePtr> & neighborPtrSets, vector<double> & edgeCostSets)
{   
    neighborPtrSets.clear();
    edgeCostSets.clear();

   Eigen::Vector3i current_index = currentPtr->index;
   double current_x = current_index[0];
   double current_y = current_index[1];
   double current_z = current_index[2];
   Eigen::Vector3d current_coordinate = currentPtr->coord;
   double neighbor_x;
   double neighbor_y;
   double neighbor_z;
   GrideNodePtr tmp_ptr = NULL;
   Eigen::Vector3d neighbor_coordinate = tmp_ptr->coord;
   double distance;

   for(int i = -1; i <= 1; i++){
        for(int j = -1; j <= 1; j++){
            for(int k = -1; k <= 1; k++){
                if(i == 0 && j == 0 && k == 0)
                {
                    continue;
                }
                
                neighbor_x = current_x + i;
                neighbor_y = current_y + j;
                neighbor_z = current_z + k;

                // 防止x和y以及z的索引越界
                if(neighbor_x < 0 || neighbor_x > (GLX_SIZE - 1) || neighbor_y < 0 || neighbor_y > (GLY_SIZE - 1) ||
                neighbor_z < 0 || neighbor_z < (GLZ_SIZE - 1))
                {
                    continue;
                }

                // 邻居节点为障碍物跳过它，不加入open list
                if(isOccupied(neighbor_x, neighbor_y, neighbor_x))
                {
                    continue;
                }

                tmp_ptr = GridNodeMap[neighbor_x[0]][neighbor_x[1]][neighbor_x[2]];

                // id = -1表示在closed list中
                if(tmp_ptr->id == -1)
                {
                    continue;
                }

                distance = std::sqrt((current_x - neighbor_x) * (current_x - neighbor_x) + 
                            (current_y - neighbor_y) * (current_y - neighbor_y) + 
                            (current_z - neighbor_z) * (current_z - neighbor_z));

                distance = 1.0001 * distance; // Tie breaker嘛

                neighborPtrSets.push(tmp_str);
                edgeCostSets.push(distance);

            }
        }
   }

}

将当前的节点的index在x和y、z方向上都做+1或-1操作，搜索周围的几何邻居，同时看邻居是否在GridNodeMap的边界以及邻居是否为障碍物，这些都不加入open list中，同时计算当前节点与终点的距离，最终将可访问的邻居加入open list中， 距离加入edgeCostSets中，方便后面更新。

4.5 循环里加入扩展节点，更新open list的节点f值

for(int i = 0; i < (int)neighborPtrSets.size(); i++){
           
            Judge if the neigbors have been expanded
            please write your code below
            
            IMPORTANT NOTE!!!
            neighborPtrSets[i]->id = -1 : unexpanded
            neighborPtrSets[i]->id = 1 : expanded, equal to this node is in close set
          
           neighborPtr = neighborPtrSets[i];
            if(neighborPtr -> id == 0){ //discover a new node, which is not in the closed set and open set
               
                neighborPtr -> gScore = currentPtr -> gScore + edgeCostSets[i];
                neighborPtr -> fScore = neighborPtr -> gScore + getHeu(startPtr, neighborPtr);   
                neighborPtr -> cameFrom = currentPtr;
                neighborPtr -> coord = gridIndex2coord(neighborPtr->index);
                openSet.insert( make_pair(neighborPtr -> fScore, neighborPtr) );
                neighborPtr -> id = 1; 
                continue;
            }
            else if(neighborPtr -> id == 1){ //this node is in open set and need to judge if it needs to update, the "0" should be deleted when you are coding
             
               // 不太理解这个openSet里移除iter，再加入neighborPtraw
                if(neighborPtr -> gScore > currentPtr -> gScore + edgeCostSets[i])
                {
                    auto ptr = openSet.equal_range(neighborPtr->fScore);
                    neighborPtr -> gScore = currentPtr -> gScore + edgeCostSets[i];
                    neighborPtr -> fScore = neighborPtr -> gScore + getHeu(startPtr, neighborPtr);
                    neighborPtr -> cameFrom = currentPtr;
                    if(ptr.first != end(openSet))
                    {
                        for(auto iter = ptr.first; iter != ptr.second; ++iter){
                            if(iter->second->index == neighborPtr->index)
                            {
                                openSet.erase(iter);
                                openSet.insert(make_pair(neighborPtr -> fScore, neighborPtr));
                            }
                        }
                    }
                }

                continue;
            }
            else{
                continue;
            }
        }      
    }
    //if search fails
    ros::Time time_2 = ros::Time::now();
    if((time_2 - time_1).toSec() > 0.1)
        ROS_WARN("Time consume in Astar path finding is %f", (time_2 - time_1).toSec() );
}

首先是在neighborPtr中拿出一个节点，该节点neighborPtr -> id如果为0的话，说明该节点还没有被访问过，那么就计算它的f值、g值以及把它的父节点记为当前节点，同时把它加入openSet中，id记为1；
那么id如果为1的话，说明该节点在open list中，那么我们需要更新该节点的f值，同时把open list的节点f值重新排序。

4.6 回溯找到最优路径的节点，打印出路径

vector<Vector3d> AstarPathFinder::getPath() 
{   
    vector<Vector3d> path;
    vector<GridNodePtr> gridPath;
   
   auto middlePtr = terminatePtr;
   while(middlePtr->cameForm != NULL)
   {
        gridPath.push_back(middlePtr);
        middlePtr = middlePtr->cameForm;
   }

    for (auto ptr: gridPath)
        path.push_back(ptr->coord);
        
    reverse(path.begin(),path.end());

    return path;
}

从当前节点开始循环去找父节点，直到没有父节点，也就是起点，把所有节点的坐标加入数组中，同时逆序输出这个数组，就是我们需要的起点到终点的路径。
本文介绍了Dijkstra算法、A*、JPS算法，以及Dijkstra算法、A*算法的代码实现，感谢观看。