蓝桥杯---第二讲---二分与前缀和

---

前言

本篇博客主要打卡记录博主学习蓝桥杯C++AB组辅导课的习题第一章节的题目。

---

Ⅰ. 数的范围

0x00 算法思路

详细可以看下这一篇博客，详细讲解了二分算法知识
【algorithm】算法基础课—二分查找算法（附笔记 | 建议收藏）

0x00 代码书写

#include 

using namespace std;

const int maxn = 100005;
int n, q, x, a[maxn];

int main() 
{
    scanf("%d%d", &n, &q);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);
    while (q--) 
    {
        scanf("%d", &x);
        int l = 0, r = n - 1;
        while (l < r) 
        {
            int mid = l + r >> 1;
            if (a[mid] < x)  l = mid + 1;
            else    r = mid;
        }
        if (a[l] != x) 
        {
            printf("-1 -1\n");
            continue;
        }
        int l1 = l, r1 = n;
        while (l1 + 1 < r1) 
        {
            int mid = l1 + r1 >> 1;
            if (a[mid] <= x)  l1 = mid;
            else    r1 = mid;
        }
        printf("%d %d\n", l, l1);
    }
    return 0;
}

Ⅱ. 数的三次方根

0x00 算法思路

1.迭代的思路，就是无脑迭代100次就可.
2.根据题目法写的方法，其实这个就是while(r-l>谁就行啦).

0x01代码书写

#include
#include

using namespace std;

int main()
{
    double n;
    scanf("%lf",&n);
    double l = -100000, r = 100000;
    while(r - l > 0.00000001)
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= n) r = mid;
        else l = mid;
    }
    printf("%.6lf",l);
    
    return 0;
}

Ⅲ. 前缀和

0x00 算法思路

详细知识看算法基础课笔记 前缀和与差分
【algorithm】认真讲解前缀和与差分 (图文搭配)

0x01 代码书写

#include

using namespace std;

int n,m;
int sum[100010];

int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
    {
        int tmp;
        cin>>tmp;
        sum[i]=sum[i-1]+tmp;
    }

    while(m--)
    {
        int l,r;
        cin>>l>>r;
        cout<<sum[r]-sum[l-1]<<endl;
    }
    return 0;
}

Ⅳ. 子矩阵的和

0x00 算法思路

详细知识看算法基础课笔记 前缀和与差分
【algorithm】认真讲解前缀和与差分 (图文搭配)

0x01 代码书写

#include

using namespace std;

int n,m,q;
int s[1010][1010];

int main()
{
    cin>>n>>m>>q;

    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        cin>>s[i][j];
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
        }
    }

    while(q--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;
    }

    return 0;
}

Ⅴ. 机器人跳跃问题

0x00 算法思路

这一道题主要考查了二分答案的算法，通过物理计算得到不论是从低到高，还是从高到低都是：e = 2 * e - h[i] 所以我们假设有一个临界点 E0 满足 0 ~ E0 能量是不满足的，E0 ~ 0x3f3f3f3f 是满足的，就可以使用y总的二分模板了。

0x01 代码书写

#include

using namespace std;

const int N = 100010;

int n;
int h[N];

bool check(int e)
{
    for(int i = 1 ; i <= n ; ++ i)
    {
        e = e * 2 - h[i];
        if(e >= 1e5) return true;//防止爆int
        else if(e < 0) return false;    
    }
    return true;
}

int main()
{
    cin >> n;
    for(int i = 1 ; i <= n ; ++ i) cin >> h[i];

    int l = 0 , r = 1e5;
    while(l < r)
    {
        int mid = l + r >> 1;

        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << r << endl;

    return 0;
}

Ⅵ. 四平方和

0x00 算法思路

这一道题我没学具体的算法思路，感觉不如暴力来的实在，确信哈哈哈

0x01 代码书写

#include
#include

using namespace std;

int n;
int a,b,c,d;

int main()
{
    scanf("%d",&n);

    for(int a=0;a*a<=n;a++)
    {
        for(int b=a;a*a+b*b<=n;b++)
        {
            for(int c=b;a*a+b*b+c*c<=n;c++)
            {
                int t=n-a*a-b*b-c*c;
                int d=sqrt(t);
                if(d*d==t)
                {
                    printf("%d %d %d %d\n",a,b,c,d);
                    return 0;
                }
            }
        }
    }

    return 0;
}

Ⅶ. 分巧克力

0x00 算法思路

这道题主要考查了二分算法，主要是对于一块大巧克力进行分割，思考的到，当分割的块数越多，边长就越短，块数越少，边长就越大，所以肯定可以有一个临界点 mid 可以使得刚好的块数 满足要求 刚好 >= k 块 如果边长 在 Left ~ mid 之间的话 就是边长很大 所以check函数可以判断这个， 如果在 mid ~ Right 之间的话 肯定是都满足要求的。 最后套用y总的算法模板即可

0x01 代码书写

#include

using namespace std;

const int N = 100010;

int n,k;
int h[N],w[N];

bool check(int mid)
{
	int res = 0;
	for(int i = 0 ; i < n ; ++ i)
	{
		res += (long long)h[i] / mid * (w[i] / mid);
		if(res >= k) return true;
	}
	return false;
}

int main()
{
	cin >> n >> k;
	
	for(int i = 0 ; i < n ; ++ i) cin >> h[i] >> w[i];
	
	int l = 1 , r = 1e5;
	
	while(l < r)
	{
		int mid = l + r + 1 >> 1;
		if(check(mid)) l = mid;
		else r = mid - 1;
	}
	cout << r << endl;
	
	return 0;
}

Ⅷ. 激光炸弹

0x00 算法思路

贴一个acwing的图片 ： 链接 ： AcWing 99. 激光炸弹第一题解

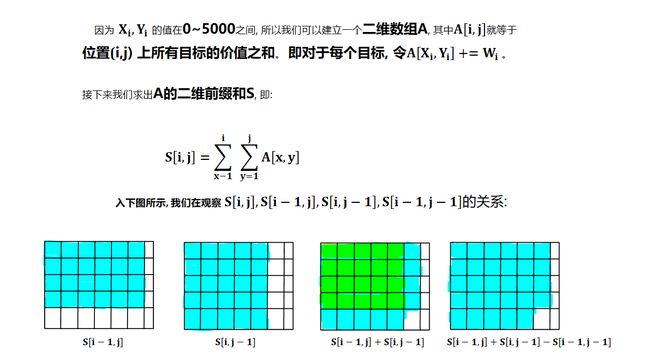
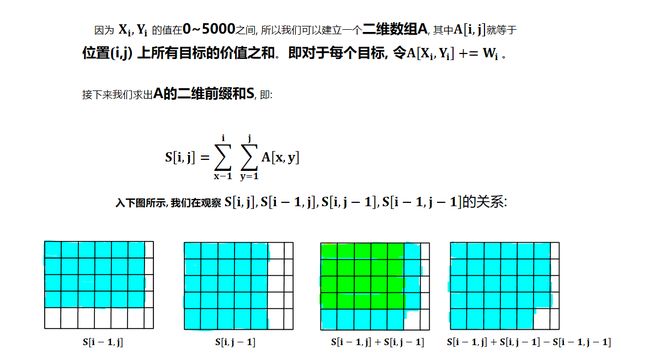
0x01 代码书写

#include

using namespace std;

const int N = 5010;
int cnt,r;
int s[N][N];
int n,m;

int main()
{
    cin >> cnt >> r;
    r=min(r,5001);
    n = m = r;
    
    while(cnt --)
    {
        int x,y,w;
        cin >> x >> y >> w;
        x ++;
        y ++;
        n = max(x,n);
        m = max(y,m);
        
        s[x][y] += w;
    }
    
    for(int i = 1; i <= n; ++ i)
        for(int j = 1; j <= m ;++ j)// 构造二维前缀和
            s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];
            
    int res = 0;      
    
    for(int i = r; i <= n ;++ i)
    {
        for(int j = r; j <= m ;++ j)//根据二维前缀和进行答案计算
        {
            res = max(res, s[i][j]-s[i-r][j]-s[i][j-r]+s[i-r][j-r]);
        }
    }
    cout << res << '\n';
    return 0;
}

Ⅸ. K倍区间

0x00 算法思路

这一道题我只是用了 前缀和做优化，感觉我考试的时候也想不到y总的算法思路，呜呜呜呜呜…

0x01 代码书写

#include

using namespace std;

int n,k;
int a[100010];
int sum[100010];

int main()
{
    cin>>n>>k;

    for(int i=1;i<=n;i++) cin>>a[i];

    int ans=0,i=0;
    for(i=1;i<=n;i++)
    {
        sum[i]=sum[i-1]+a[i];
    }

    for(int j=1;j<=i;j++)
    {
        for(int s=j+1;s<=i;s++)
        {
            if((sum[s]-sum[j])%k==0) // 前缀和优化
            {
                ans++;
            }
            else continue;
        }
    }
    cout<<ans;
    return 0;
}

---

总结

本篇博客主要讲解了前缀和 和 二分算法的知识，前面四道题都是算法基础课 的模板题，后面几道题才是真正考查这两个算法的真实难度，开始我也觉得很难很难，但是认真学习完发现其实还是可以学会的，所以请热爱 请认真学习，总会学好，总会获得不小的进步的，加油吧夏目浅石.