哈希应用之位图
文章目录
- 1.位图概念
- 2.面试题引入
- 3.代码解决[配注释]
- 4.位图应用
-
- 4.1找到100亿个整数里只出现一次的整数
- 4.2找两个分别有100亿个整数的文件的交集[只有1G内存]
-
- 1.法一[使用于数据量<=42亿]
- 2.法二[适用于数据量大>42亿]
- 3.在一个有100亿个int的文件中找到出现次数不超过2次的所有整数[1G内存]
- 5.优劣分析
-
- 优点
- 缺点
1.位图概念
位图,用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据是否存在于海量数据.
2.面试题引入
例如: 经典面试题[腾讯]
现在有40亿个不重复的无符号整数,没排过序。如何快速判断一个无符号整数是否在这40亿个数中。
思考:
1.暴力查找 40亿次
2.排序+二分 最优排序O(N*logN) 二分logN [且二分查找要支持下标访问 文件无法下标查找]
3.哈希表/红黑树 使用的前提是数据在它里面 而40亿整数大小为16G 无法使用
怎么办???面试要挂了吗???要与大厂失之交臂了吗???
不!我要进大厂!那就往下学一下位图!!!
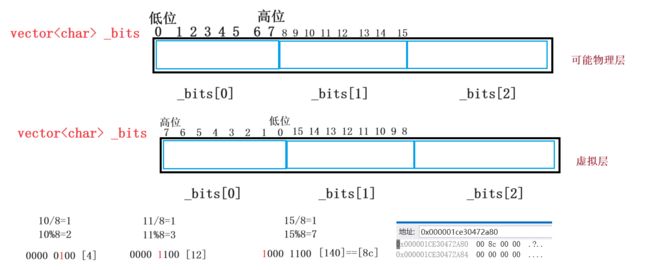
一个无符号整数X是否在给定的整形数据中,需要得到的结果是在或者不在,是两种状态,可以使用一个二进制比特位来代表数据是否存在,假定二进制比特位为1,代表存在,为0代表不存在。这样一个字节8个比特位可以存储8个整数 40亿个整数需要多大空间呢?容易得到的是1G=10亿字节=80亿比特位 一个比特位存储一个整数 40亿个整数需要40亿个比特位 即0.5G
3.代码解决[配注释]
//一个比特位变标识两种状态 0 1
template<size_t N>
class bitmap
{
public:
//构造函数
bitmap()
{
//开空间 初始化成0
_bits.resize(N / 8 + 1, 0);
}
//插入: 将数x映射的位 置成1
void insert_setone(size_t x)
{
//第i个字节 0 1 2 3 ...
size_t i = x / 8;
//第i个字节的第j个位
size_t j = x % 8;
//利用或等 第j位-置1 其余位-不变
_bits[i] |= (1 << j); //左移:并不是向左移而是向高位移
}
//删除: 将数x映射的位 置成0
void erase_setzero(size_t x)
{
//第i个字节 0 1 2 3 ...
size_t i = x / 8;
//第i个字节的第j个位
size_t j = x % 8;
//利用与等 第j位-置0 其余位-不变
_bits[i] &= ~(1 << j);
}
//判断: 判断数x是否存在
bool judge(size_t x)
{
//第i个字节 0 1 2 3 ...
size_t i = x / 8;
//第i个字节的第j个位
size_t j = x % 8;
//假定数x存在 那么第j位应为1
//_bits[i]访问到的是 数x所在第i个字节的整体数
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
测试函数 ///
void test_bitmap1()
{
bitmap<100> bm;
bm.insert_setone(10);
bm.insert_setone(11);
bm.insert_setone(15);
cout << bm.judge(10) << endl;
cout << bm.judge(15) << endl;
bm.erase_setzero(10);
cout << bm.judge(10) << endl;
cout << bm.judge(15) << endl;
bm.erase_setzero(10);
bm.erase_setzero(15);
cout << bm.judge(10) << endl;
cout << bm.judge(15) << endl;
}
void test_bitmap2()
{
//4294967295
//bitset<-1> bm;
bitmap<0xFFFFFFFF> bm;
}
4.位图应用
4.1找到100亿个整数里只出现一次的整数
/// 找到100亿个整数里只出现一次的整数
//两个比特位变标识三种状态 00-不存在 01-存在一个 10-存在多个
template<size_t N>
class double_bitmap
{
public:
//插入函数 -- 映射位置1
void insert_setone(size_t x)
{
//数x 第一次进来定走这个if
// 00 -> 01 原无此数 现有一次
if (_left.judge(x) == false
&& _right.judge(x) == false)
{
//_right映射位 置1
_right.insert_setone(x);
}
//第二次又来了一个相同数x 走这个else if
// 01 -> 10 原有一次 现有两次
else if (_left.judge(x) == false
&& _right.judge(x) == true)
{
//_left映射位 置1
//_right映射位 置0
_left.insert_setone(x);
_right.erase_setzero(x);
}
//10 :存在多个的数 不用处理 10是多个 再插入一个 还是多个 10
}
//输出只存在一次的数
void Print()
{
for (size_t i = 0; i < N; ++i)
{
if (_right.judge(i))
cout << i << endl;
}
}
public:
bitmap<N> _left;
bitmap<N> _right;
};
/// 测试函数
void test_doublebitmap()
{
int a[] = { 3, 45, 53, 32, 32, 43, 3, 2, 5, 2, 32, 55, 5, 53, 43, 9, 8, 7, 8 };
double_bitmap<100> double_bm;
for (auto e : a)
{
double_bm.insert_setone(e);
}
double_bm.Print();
}
4.2找两个分别有100亿个整数的文件的交集[只有1G内存]
1.法一[使用于数据量<=42亿]
N+N
时间复杂度与数据个数有关
Step1:将文件一的数据以位图一存储
Sterp2:将文件二的数据一一读取 调用judge函数 判断是否存在于文件一的位图中 若存在 则是交集 将位图一对应位 置成0[当前数已被认定是交集 为防止文件二有重复值 下个与当前数相同的数再来judge时 认定为不存在—去重]
2.法二[适用于数据量大>42亿]
2N+42亿
时间复杂度还与N有关[2^32-1]
计算机知识:计算机所能存储的最大整数:int 在32位机器下 int是4个字节 32个bit 2^32-1
Step1:将文件一的数据映射到位图一
Step2:将文件二的数据映射到位图二
Step3:遍历N[因为100亿个数可能存在计算机所能够存储的42亿个整数里的任意一个 所以要遍历42亿个bit
位] 若两个位图对应位均为1 则为交集
3.在一个有100亿个int的文件中找到出现次数不超过2次的所有整数[1G内存]
用两个bit来标识即可
00:出现0次
01:出现1次
10:出现2次
11:出现2次及以上
5.优劣分析
优点
时间复杂度 空间复杂度小
缺点
只能映射整型 浮点数\string不能用位图