一文搞懂时间序列ARIMA模型
文章目录
-
- 1 ARIMA的定义
- 2 差分(differencing)
-
- 2.1 Order:差分的阶数
- 2.2 Lag:差分的滞后
- 2.3 滞后运算/滞后算子/延迟算子
- 2.4 关于差分的两个误解
- 3 ARIMA的平稳性
- 4 ACF与PACF
- 5 时序模型的选择与评估
-
- 5.1 超参数p、q、d的确定
- 5.2 时间序列的评估指标
1 ARIMA的定义
AR模型相信“历史决定未来”,因此很大程度上忽略了现实情况的复杂性、也忽略了真正影响标签的因子带来的不可预料的影响。而相对的,MA模型相信“时间序列是相对稳定的,时间序列的波动是由偶然因素影响决定的”,但现实中的时间序列很难一直维持“稳定”这一假设。基于此,ARIMA模型对以上两个模型进行了“组合”,ARIMA模型的基本思想是:一个时间点上的标签值既受过去一段时间内的标签值影响,也受过去一段时间内的偶然事件的影响。即ARIMA模型假设为标签值是围绕着时间的大趋势而波动的,其中趋势是受历史标签影响构成的,波动是受一段时间内的偶然事件影响构成的,且大趋势本身不一定是稳定的。在这个中心思想的引导下,ARIMA模型的公式被表示为:
y t = β 0 + β 1 y t − 1 + β 2 y t − 2 + … + β p y t − p + ϵ t + θ 1 ϵ t − 1 + θ 2 ϵ t − 2 + … + θ q ϵ t − q y_{t}=\beta_{0}+\beta_{1}y_{t-1}+\beta_{2}y_{t-2}+…+\beta_{p}y_{t-p}+\epsilon_{t}+\theta_{1}\epsilon_{t-1}+\theta_{2}\epsilon_{t-2}+…+\theta_{q}\epsilon_{t-q} yt=β0+β1yt−1+β2yt−2+…+βpyt−p+ϵt+θ1ϵt−1+θ2ϵt−2+…+θqϵt−q
在这个简单粗暴的公式中,各个变量的含义与MA、AR模型中完全相同,且各个变量的求解方式与原始MA、AR模型基本相同。很明显,公式的前半段是AR模型,后半段是MA模型中关于“波动”的部分。值得注意的是,MA模型中代表长期趋势的均值并不存在于ARIMA模型的公式当中,因为ARIMA模型中“预测长期趋势”这部分功能由AR模型来执行,因此AR模型替代了原本的。在ARIMA模型中, β 0 \beta_{0} β0可以为0。
以上模型被称之为ARIMA(p,d,q)模型,其中p和q的含义与原始MA、AR模型中完全一致,且p和q可以被设置为不同的数值,而d是ARIMA模型需要的差分的阶数。
2 差分(differencing)
差分是一种用于序列的数学运算,对一个序列进行差分运算,即是计算该序列中的不同观测值之间的差异。举例说明,假设现在有序列X:
X = [ 5 , 4 , 6 , 7 , 9 , 12 ] X − = [ 5 , 4 , 6 , 7 , 9 , 12 ] X=[5,4,6,7,9,12]\\ X_{-}=[5,4,6,7,9,12] X=[5,4,6,7,9,12]X−=[5,4,6,7,9,12]
如果让该序列中执行4-5、6-4、7-6、9-7、12-9五组运算,即后一位数减前一位数,形成新的序列X’,则有:
X ′ = [ − 1 , 2 , 1 , 2 , 3 ] X'=[-1,2,1,2,3] X′=[−1,2,1,2,3]
则序列X’就是序列X的一阶差分结果(First-Order Differencing)。不难发现,一阶差分运算就是令序列中索引更大的值减去与其相邻的索引更小的值,且形成新序列的运算。当序列是时间序列时,一阶差分运算在计算的就是相邻时间点上的标签值的差异。和原始序列相比,差分后序列往往位数更少(序列更短),通常进行一次差分运算,原始的序列会变短1个单位。
在实际进行差分运算时,我们可以改变差分运算的两个相关因子来执行不同的差分:一个是差分的阶数(order),另一个是差分的滞后(lag)。
2.1 Order:差分的阶数
高阶差分意味着多次执行一阶差分。例如,当对X[5, 4, 6, 7, 9, 12]进行二阶差分时(Second-Order Differencing),实际上是需要对X进行两次一阶差分,即先求解出X’,再在X’的基础上进行一阶差分,求解出X’‘:
X ′ = [ − 1 , 2 , 1 , 2 , 3 ] X ′ ′ = [ 3 , − 1 , 1 , 1 ] X'=[-1,2,1,2,3]\\ X''=[3,-1,1,1] X′=[−1,2,1,2,3]X′′=[3,−1,1,1]
此时X’'的结果就是序列X的二阶差分。因此,n阶差分就是在原始数据基础上进行n次一阶差分。在现实中,我们使用的高阶差分一般阶数不会太高。在ARIMA模型中,超参数最常见的取值是0、1、2这些很小的数字。
2.2 Lag:差分的滞后
差分的滞后(lag)与差分的阶数完全不同。正常的一阶差分是滞后为1的差分(lag-1 Differences),这代表在差分运算中,让相邻的两个观测值相减,即让间隔为(lag-1)的两个观测值相减。因此,当滞后为2时,则代表需要让相隔1个值的两个观测值相减。举例说明:
X = [ 5 , 4 , 6 , 7 , 9 , 12 ] X=[5,4,6,7,9,12] X=[5,4,6,7,9,12]
假设现在我们对序列X执行滞后2差分(lag-2 Differences),求得X_lag_2,则是在该序列中执行6-5、7-4、9-6、12-7的运算,最终我们得到的序列是:
X l a g 2 = [ 1 , 3 , 3 , 5 ] X_{lag2}=[1,3,3,5] Xlag2=[1,3,3,5]
序列 X l a g 2 X_{lag2} Xlag2就是序列X的滞后2差分结果。因此,滞后的差分运算就是令序列中索引更大的值减去与其相隔(lag-1)个样本的索引更小的值,而形成新序列的运算。不难发现,滞后的差分得到的结果位数会等于len(X) - lag,因此之后的差分序列会比原始序列短lag个单位。
带滞后的差分也叫做多步差分,例如,滞后为2的差分就叫做2步差分。相比起平时不怎么使用的高阶差分,多步差分应用非常广泛。在时间序列中,标签往往具备一定的周期性:例如,标签可能随季节有规律地波动(比如在夏季标签值高、在冬季标签值较低等),也可能随一周的时间有规律地波动(比如在周末较高、在工作日较低等)。这种波动可以通过滞后差分来消除,例如下面的数据:
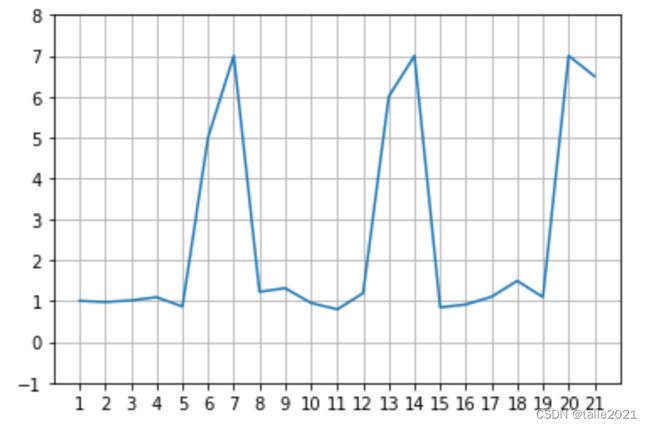
X = [1.01,0.98,1.02,1.1,0.87,5,7,1.23,1.32,0.96,0.80,1.2,6,7,0.85,0.92,1.11,1.5,1.1,7,6.5]
plt.plot([*range(1,len(X)+1)],X)
plt.xticks(ticks = [*range(1,len(X)+1)])
plt.ylim((-1,8))
plt.grid();
使用该数据绘制图像,则会看到明显的规律:这一数据是按照7天为周期波动的,每到7天的最后2天则会出现高峰,其他时间则均匀地维持在1左右。如果对该数据做滞后为7的差分,则会明显改变数据的分布情况。在Python中,可以使用DataFrame自带的Shift功能来完成差分运算:
lag_7_d = pd.DataFrame(X) - pd.DataFrame(X).shift(7)
plt.plot([*range(1,lag_7_d.notnull().sum()[0])],lag_7_d.iloc[8:,0])
plt.ylim((-1,8))
plt.grid();
很明显,差分运算可以消除数据中激烈的波动,因此可以消除时间序列中的季节性、周期性、节假日等影响。一般我们使用滞后为7的差分消除星期的影响,而使用滞后为12的差分来消除月份的影响(一般这种情况下每个样本所对应的时间单位是月),我们也常常使用滞后4来尝试消除季度所带来的影响。在统计学中,差分运算本质是一种信息提取方式,其最擅长提取的关键信息就是数据中的周期性,和其他信息提取方式一样,它会舍弃部分信息、提炼出剩下的信息供模型使用。也因此,差分最重要的意义之一就是能够让带有周期性的数据变得平稳,在任何的统计学教材中,我们都可以找到众多的证据来证明这一点: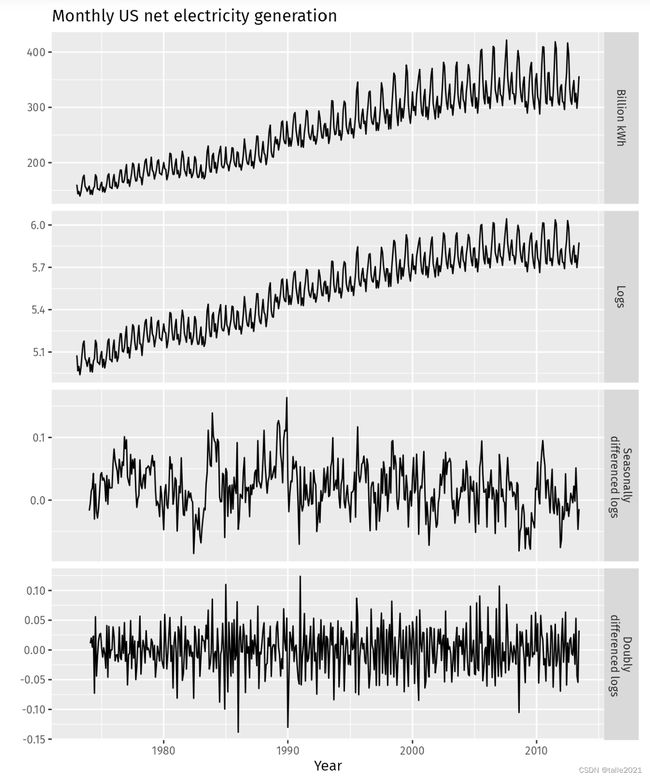
2.3 滞后运算/滞后算子/延迟算子
滞后(lag)这一概念是差分运算中的关键概念,但事实上,独立于差分运算之外,滞后也是统计学中重要的运算形式之一。在统计学中,滞后运算是“向后移动一个单位”的运算,当用于时间序列时,它特指“向过去移动一个时间单位”的运算。大部分时候,滞后运算被简写为字母B(Backshift)或者字母L(Lag),我们可以对单一的时序样本或整个时间序列做滞后运算。举例说明,对于一个时间点上的标签值,有:
B y t = y t − 1 By_{t}=y_{t-1} Byt=yt−1
并且:
B ( B y t ) = B 2 y t = y t − 2 B(By_{t})=B^2y_{t}=y_{t-2} B(Byt)=B2yt=yt−2
对整个时间序列有:
t s = [ y t − 2 , y t − 1 , y t , y t + 1 , y t + 2 ] B ( t s ) = [ y t − 3 , y t − 2 , y t − 1 , y t , y t + 1 ] ts=[y_{t-2},y_{t-1},y_{t},y_{t+1},y_{t+2}]\\ B(ts)=[y_{t-3},y_{t-2},y_{t-1},y_{t},y_{t+1}] ts=[yt−2,yt−1,yt,yt+1,yt+2]B(ts)=[yt−3,yt−2,yt−1,yt,yt+1]
因此滞后运算可以被用来表现差分。其中,多步差分的表现方式很简单,一步差分是相邻的标签值之间相减,因此有1-lag difference:
1 − l a g − y = y t − y t − 1 = y t − B y t = ( 1 − B ) y t 1_{-}lag_{-}y=y_{t}-y_{t-1}=y_{t}-By_{t}=(1-B)y_{t} 1−lag−y=yt−yt−1=yt−Byt=(1−B)yt
12步差分是相隔11个标签值进行相减,因此有12-lag difference:
1 2 − l a g − y = y t − y t − 12 = y t − B 12 y t = ( 1 − B 12 ) y t 12_{-}lag_{-}y=y_t-y_{t-12}=y_{t}-B^{12}y_{t}=(1-B^{12})y_{t} 12−lag−y=yt−yt−12=yt−B12yt=(1−B12)yt
因此n步差分就可以表示为:
n − l a g − y = ( 1 − B n ) y t n_{-}lag_{-}y=(1-B^{n})y_{t} n−lag−y=(1−Bn)yt
与之相对的,高阶差分也可以用滞后运算表示。假设现在有时序数据:
[ y t − 2 , y t − 1 , y t , y t + 1 , y t + 2 ] [y_{t-2},y_{t-1},y_{t},y_{t+1},y_{t+2}] [yt−2,yt−1,yt,yt+1,yt+2]
整个序列的一阶差分为:
[ ( y t − 1 − y t − 2 ) , ( y t − y t − 1 ) , ( y t + 1 − y t ) , ( y t + 2 − y t + 1 ) ] [(y_{t-1}-y_{t-2}),(y_{t}-y_{t-1}),(y_{t+1}-y_{t}),(y_{t+2}-y_{t+1})] [(yt−1−yt−2),(yt−yt−1),(yt+1−yt),(yt+2−yt+1)]
一阶差分就等同于一步差分,因此有first-order difference:
y ′ = y t − y t − 1 = y t − B y t = ( 1 − B ) y t y'=y_{t}-y_{t-1}=y_{t}-By_{t}=(1-B)y_{t} y′=yt−yt−1=yt−Byt=(1−B)yt
在此基础上,二阶差分可以被表示为second-order difference:
y " = ( y t − y t − 1 ) − ( y t − 1 − y t − 2 ) = y t − 2 y t − 1 + y t − 2 = y t − 2 B y t + B 2 y t = ( 1 − 2 B + B 2 ) y t = ( 1 − B ) 2 y t \begin{split} y"&=(y_{t}-y_{t-1})-(y_{t-1}-y_{t-2})\\ &=y_{t}-2y_{t-1}+y_{t-2}\\ &=y_{t}-2By_{t}+B^{2}y_{t}\\ &=(1-2B+B^{2})y_{t}\\ &=(1-B)^{2}y_{t} \end{split} y"=(yt−yt−1)−(yt−1−yt−2)=yt−2yt−1+yt−2=yt−2Byt+B2yt=(1−2B+B2)yt=(1−B)2yt
以此类推,d阶差分可以被表示为:
d − o r d e r − y = ( 1 − B ) d y t d_{-}order_{-}y=(1-B)^{d}y_{t} d−order−y=(1−B)dyt
在该公式中的也正是ARIMA模型中的超参数,因此滞后运算和差分运算是紧密相连的。当我们在ARIMA模型中输入参数d=任意数字时,实际上大部分算法库会按照上面的公式直接对时序数据进行滞后运算。滞后是能够实现差分运算的、更加简单和高效的运算方法。
在实际使用中,我们经常将多步差分和高阶差分混用,最典型的就是在ARIMA模型建模之前:一般我们会先使用多步差分令数据满足ARIMA模型的基础建模条件,再在ARIMA模型中使用低阶的差分帮助模型更好地建模。例如,先对数据进行12步差分、再在模型中进行1阶差分,这样可以令数据变得平稳的同时、又提取出数据中的周期性,极大地提升模型对数据的拟合精度。
2.4 关于差分的两个误解
-
差分的阶数越高、步数越多,提炼出的信息就越精华。
事实上,和众多信息提取的过程一样,差分在提取信息的过程中也会产生信息的损失、甚至提炼出“噪音”。阶数越高、步数越多,差分运算丢失的原始信息就会越多,信息的“形变”也就会越厉害,因此我们需要找到合适的阶数和步数,而不是坚持使用高阶或多步差分。
当阶数过高或步数过多导致数据的信息被无谓浪费时,称这样的情况为“过差分”(overdifferencing)。过差分有两个基本的信号:差分后数据的方差变得很高,或者样本之间的相关性明显被削弱。这种情况下则要选择阶数更低、步数更少的差分。
-
只要数据具有趋势性/周期性,就可以利用差分运算将其消除。
差分运算的确可以被应用到大部分有趋势性、周期性的时间序列数据上,但它不能解决所有时序数据的问题。首先,不是所有时序模型都要求数据是无趋势性、无周期性的状态,即便模型要求了,当差分运算不管用时,也可以使用其他方式消除数据的周期性和趋势性。
比如如果数据存在季节性,我们可以从每个观测值中减去当季所有观测点的均值,如果数据是月度数据,我们则可以让每月的观测值减去当月的均值,以此类推。如果数据随时间波动,形成类似于三角函数的波动,那我们可以让每个观测点除以周围的波动率,以消除峰值。总之,需要具体情况具体分析,同时积累时序数据处理的经验。
3 ARIMA的平稳性
为何ARIMA模型要内置差分运算、甚至将差分的阶数设置为ARIMA关键的超参数之一呢?因为差分运算带来的平稳性是ARIMA模型能够顺利运行的基本要求。具体地来说,ARIMA模型具有如下基本假设:输入ARIMA的时间序列数据必须是平稳的(stationary)数据。
在统计学上,平稳时间序列的定义如下:**在一段时间序列中,无论时间如何变化,该序列的标签值的统计特性,如均值、方差、协方差等属性都保持不变,那这段时间序列就是平稳的。**即是说,在一段稳定的时序数据上,即便随机地取出长度不同、起点不同、终点不同的时序数据,这些数据的统计特性都会表现得完全一致。根据这一定义,平稳数据的内在规律、统计特性等不会随时间改变,因此在平稳的数据上,过去的规律可以被推广到任意未来的时间段中去使用,这奠定了未来时间中的标签值可以被预测的基础。
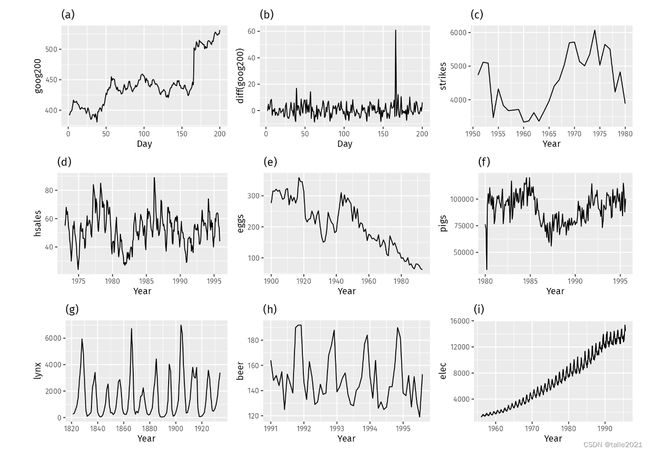
通过绘制图像,可以大致辨别数据是否满足统计学上要求的稳定性——
在统计学上,稳定的时序数据是指始终围绕着一个均值波动,且波动的幅度变化不是很大的数据(例如,上图中红色的序列就是一个比较接近平稳序列的序列)。因此,在时间变化的同时,序列标签均值明显变化,或不同阶段的波动幅度明显有差异、不均匀的数据都是不稳定的。具体来说,数据有明显的上升趋势,或下降趋势、数据呈现季节性、周期性、或波动幅度明显越来越大、越来越小的时候,数据都是不稳定的。
不过需要注意的是,有些图像可能展现出明显的周期性,但却是符合稳定性要求的——当图像有周期性,但周期性的表象却是由某些不可控的事件偶然导致、且我们无法预料下一个周期是否还会出现相同的周期性表现时,那数据可能是符合稳定性要求的。同时,数据中存在一些异常值,并不影响数据的稳定性。
很明显,图像a、c、e、f和i有明显的趋势性变化,i的方差也随着时间逐渐变大,因此可以先排除这五张图。剩下的g、h看起来有明显的周期性,因此需要调研一下这些周期性是否由巧合造成,如果这些周期性不是由巧合造成,则g和h也可以排除。图d看起来也有一定的周期性,但并不像序列g和h那样明显,因此存疑。b则基本可以被认为是平稳序列,虽然中间出现了一个异常的高峰,但排除异常值的影响,b很有可能是平稳序列。
在统计学中,我们当然不太可能靠着肉眼绘图对序列的平稳性进行判断。事实上,我们需要针对平稳与否完成假设检验。当且仅当我们可以保证数据是稳定的,我们才能将数据输入ARIMA模型进行预测。在统计学中,判断时间序列是否为平稳序列的方式有三种:
- 绘制折线图:绘制图像并直观地检查是否有任何明显的趋势或季节性,如果有则大概率序列是不平稳的。
- 对时序数据进行统计并绘制直方图:计算不同时间区间中的均值和方差、并观察这些均值和方差是否有明显差异。如果各个区间中的均值方差差异很大,则序列大概率是不平稳的。
- 做统计检验:比如,在时间序列上完成DF、ADF、PP等单位根检验。
通常会使用ADF单位根检验来完成平稳性的判断,如果数据不够平稳,则需要使用差分运算消除数据中的各类趋势(但差分运算不能解决所有的问题,因此也存在着经过差分后无法变得平稳的数据。如果出现这样的情况,则需要使用取对数、减均值等方法令数据变得平稳)。当需要使用差分让数据变得平稳时,可以使用带滞后的差分、高阶差分,直到数据通过平稳性检验后,我们才能够将数据输入ARIMA模型。
4 ACF与PACF
ARIMA模型中的三个参数:p和q分别控制ARIMA模型中自回归和移动平均的部分,而d则控制输入ARIMA模型的数据被执行的差分的阶数。
y t = β 0 + β 1 y t − 1 + β 2 y t − 2 + … + β p y t − p + ϵ t + θ 1 ϵ t − 1 + θ 2 ϵ t − 2 + … + θ q ϵ t − q y_{t}=\beta_{0}+\beta_{1}y_{t-1}+\beta_{2}y_{t-2}+…+\beta_{p}y_{t-p}+\epsilon_{t}+\theta_{1}\epsilon_{t-1}+\theta_{2}\epsilon_{t-2}+…+\theta_{q}\epsilon_{t-q} yt=β0+β1yt−1+β2yt−2+…+βpyt−p+ϵt+θ1ϵt−1+θ2ϵt−2+…+θqϵt−q
通过设置p、q、d的值,可以运行一些特殊的ARIMA模型,具体来说:
| 参数设置 | ARIMA模型的实际情况 |
|---|---|
| ARIMA(p,0,0) | ARIMA等同于自回归模型AR |
| ARIMA(0,0,q) | ARIMA等同于移动平均模型MA |
| ARIMA(0,0,0) | 不建模,输出等于白噪声 ϵ t \epsilon_{t} ϵt 或等于白噪声向上或向下平移 β 0 \beta_{0} β0个单位 |
| ARIMA(0,1,0) 且不设置常数项 β 0 \beta_{0} β0 | 在白噪声基础上进行了差分处理 输出的结果等同于“随机漫步”(Random Walk) |
除了这些参数组合之外,还可以对ARIMA模型添加参数lag,以控制差分运算的滞后数(多步差分的步数)。能够执行滞后的ARIMA被称为“季节性ARIMA”,这一类ARIMA可以同时执行多步差分和高阶差分,在令时间序列稳定的同时、利用差分运算消除时间序列数据中的周期性和季节性,以达到更好的预测效果。
通过调控ARIMA模型中的超参数,可以实现不同的模型,那具体如何确定p、q、d等参数的值就需要使用自相关系数ACF(Auto-correlation function)和偏自相关系数PACF(Partial Auto-Correlation Function)了。自相关系数ACF衡量当前时间点上的观测值与任意历史时间点的观测值之间的相关性大小,而偏自相关系数PACF衡量当前时间点上的观测值与任意历史时间点的观测值之间的直接相关性的大小。在该定义中,有几个关键的问题需要解释:
1.什么是直接相关性?PACF和ACF有什么不同?
来看下面的时间序列:
t s = [ y t − 2 , y t − 1 , y t ] ts=[y_{t-2},y_{t-1},y_{t}] ts=[yt−2,yt−1,yt]
时间序列的基本原则之一是“过去影响未来”,那 y t − 2 y_{t-2} yt−2的值是如何影响了 y t y_{t} yt的值的呢?有多种可能:例如, y t − 2 y_{t-2} yt−2的值直接影响了 y t y_{t} yt的值(比如,双11当天的销量直接冲击了双11两天后的销量),也有可能 y t − 2 y_{t-2} yt−2影响了 y t − 1 y_{t-1} yt−1,再由 y t − 1 y_{t-1} yt−1将这种影响传递给 y t y_{t} yt(比如,前天的降雨量影响了昨天的降雨量,昨天的降雨量又影响今天的降雨量),还有可能两种影响都发生了,又或许 y t − 2 y_{t-2} yt−2与 y t y_{t} yt之间根本没有互相影响。在这些多种的影响方式中, y t − 2 y_{t-2} yt−2直接对 y t y_{t} yt产生的影响越大, y t − 2 y_{t-2} yt−2和 y t y_{t} yt之间的直接相关性越强。
当我们在计算ACF时,我们计算的是多种影响方式带来的“综合效应”,即ACF并不关心两个观测点之间是以什么方式相关,只关心两个观测点之间的相关程度。但PACF只关心“直接相关”的相关程度,并不关心两个观测点之间多种的、其他类型的可能的链接。因此,在求解PACF的时候,我们需要将“不直接”的相关性从ACF的值中“剔除”。
2.如何定义两个时间点之间的时间差?
在ACF和PACF的定义中,两个时间点之间的时间差可以用滞后进行衡量。比如,计算当前时间点上的观测值 y t y_{t} yt与 y t − 1 y_{t-1} yt−1之间的ACF,这样的ACF是滞后为1的ACF。如果对一个时间序列执行滞后运算,并让滞后为1的1_lag_与原始序列中的元素一一对应计算ACF,就可以一次性得出整个时间序列的滞后为1的ACF。
在实际使用这两种相关性时,我们几乎总是计算时间序列与其滞后序列之间的相关性,所以ACF和PACF值一般都是针对某一序列、在某一程度的滞后lag下计算出来的,不同的滞后lag得出的ACF/PACF值不同。当与其滞后序列k_lag_的ACF相关时,这种相关的本质其实是序列上任意时间点的观测值与(−)处的观测值相关。
3.如何理解ACF和PACF值?
与皮尔逊相关系数高度类似,ACF和PACF的取值范围都是[-1,1],其中1代表两个序列完全正相关,-1代表两个序列完全负相关,0代表两个序列不相关。通常在实际使用时,我们会依赖于代码/统计工具直接计算出不同序列的ACF和PACF值并绘制图像,再通过图像本身的表现来进行模型的选择。如下是常见的ACF(图左)和PACF(图右)的图像:
ACF图和PACF图的横坐标相同,都是不同的滞后程度,而纵坐标是当前滞后程度下序列的ACF和PACF值。背景为蓝色的区域代表着95%或99%的置信区间,当ACF/PACF值在蓝色区域之外时,我们就认为当前滞后程度下的ACF/PACF是统计上显著的值,即这个滞后程度下的序列之间的相关性很大程度上是信任的、不是巧合。当滞后为0时,ACF和PACF值必然为1,因为一个序列与自己始终完全相关,因此ACF和PACF图上有意义的值是从滞后为1的值开始看。
通常来说,ACF和PACF图有三种常见的形态:拖尾、截尾、既不拖尾也不截尾。其中,拖尾意味着图像呈现按规律衰减、自相关性呈现逐渐减弱的状态(下图左)。而截尾特指在某一个滞后程度后ACF/PACF断崖式下跌的状态(下图中),例如,滞后0、滞后1对应的ACF都很高,滞后2对应的ACF却断崖式下跌,这种情况被我们称之为“1阶截尾”。特别注意,1阶截尾/n阶截尾中的“阶”是惯用说法,实际上指的是滞后1和滞后n,千万别与高阶差分中的阶混淆。既不拖尾也不截尾的状态就是下图右,这种状况下的ACF和PACF图往往看不出什么规律。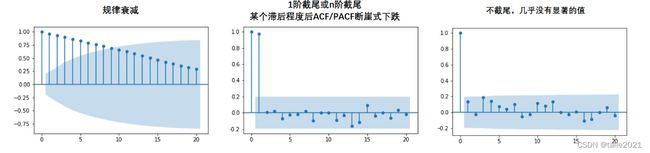
当图像呈现规律衰减的拖尾状态时,说明此时原始序列中的样本严格遵循着“久远的历史对未来的影响更弱,更近的历史对未来的影响更强”的基本常识,像这样的时间序列一定是可以用较为简单的模型进行建模的。需要注意的是,下面的情况也都属于“规律衰减的拖尾”:
当图像呈现截尾状况的时候,一般截尾的阶数都很低(一般最多不会超过3),这说明该序列中只有非常少的日子对未来有影响。当图像不截尾时,则说明原始数据中的规律较难提取,原始数据可能是平稳序列,可能是白噪音,需要更复杂的时间序列模型来进行规律的提取。
除此之外我们还可能看到其他状态的ACF和PACF图。当ACF或PACF图呈现较强的周期性时,原始序列中大概率也存在较强的周期性(比如下图,当ACF呈现三角函数一般的波动时,原始序列中大概率具有周期性)。当ACF或PACF图呈现较强的趋势性(例如上升或下降)时,原始序列中大概率也存在较强的趋势。当然,ACF和PACF图的分布并不总是忠实地反馈原始序列的状态,在实际建模时,我们需要对原始序列也进行绘图、还需要对原始数据完成各类统计检验,才能够确定原始序列的真实性质。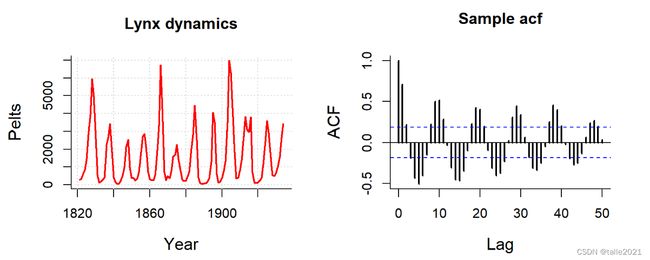
5 时序模型的选择与评估
5.1 超参数p、q、d的确定
对ARIMA模型来说,确定p和q的值有两层含义:
1)确定要使用的具体模型是AR,MA还是ARIMA?(即,p和q中任意一个值为0吗?)
2)如果是AR模型,p的值是多少?如果是MA模型,q的值是多少?如果是ARIMA模型,p和q分别是多少?
| 参数设置 | ARIMA模型的实际情况 |
|---|---|
| ARIMA(p,0,0) | ARIMA等同于自回归模型AR |
| ARIMA(0,0,q) | ARIMA等同于移动平均模型MA |
| ARIMA(p,0,q) | ARIMA模型 |
在统计学中,首先要绘制ACF和PACF图像来回答第一个问题。对任意时间序列,当ACF图像呈现拖尾、且PACF图像呈现截尾状态时,当前时间序列适用AR模型,且PACF截尾的滞后阶数就是超参数p的理想值(如下图所示,p=1)。
y t = β 0 + β 1 y t − 1 + β 2 y t − 2 + … + β p y t − p + ϵ t y_{t}=\beta_{0}+\beta_{1}y_{t-1}+\beta_{2}y_{t-2}+…+\beta_{p}y_{t-p}+\epsilon_{t} yt=β0+β1yt−1+β2yt−2+…+βpyt−p+ϵt
对AR模型,ACF的值对应了 y t − 1 y_{t-1} yt−1对 y t y_{t} yt的影响,PACF的显著性对应了的显著性
对任意时间序列,当PACF图像呈现拖尾、且ACF图像呈现截尾状态时,当前时间序列适用MA模型,且ACF截尾的滞后阶数就是超参数q的理想值(如下图所示,q=1)。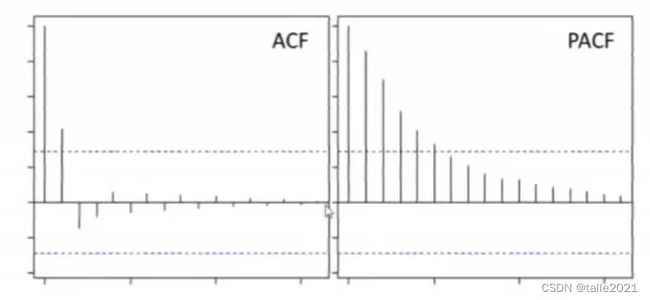
y t = β 0 + ϵ t + θ 1 ϵ t − 1 + θ 2 ϵ t − 2 + … + + θ q ϵ t − q y_{t}=\beta_{0}+\epsilon_{t}+\theta_{1}\epsilon_{t-1}+\theta_{2}\epsilon_{t-2}+…++\theta_{q}\epsilon_{t-q} yt=β0+ϵt+θ1ϵt−1+θ2ϵt−2+…++θqϵt−q
对MA模型,ACF的显著性对应了的显著性,PACF的值对应了 ϵ t − 1 \epsilon_{t-1} ϵt−1对 ϵ t \epsilon_{t} ϵt的影响
对任意时间序列,当ACF图像和PACF图像都呈现不呈现拖尾状态时,无论图像是否截尾,时间序列都适用于ARIMA模型,且此时ACF和PACF图像无法帮助我们确定p和q的具体值,但能确认p和q一定都不为0。
当确定使用AR模型时,用PACF决定p值。当确定使用MA模型时,用ACF决定q值。当确定使用ARIMA模型时,ACF和PACF是失效的,并无作用。那么当确定要使用ARIMA模型时,我们应当如何决定p和q的值呢?虽然现在统计学领域有许多理论来帮助p和q定阶,但目前实践中最好的方法依然是傻瓜式尝试。在ARIMA模型当中,p和q的值往往取值不高,一般是[1,5]以内的正整数,因此实践中更常用的方法是从最小值p=1、q=1的方式开始进行尝试,不断改变p和q的取值,直到模型通过检验或达到我们需要的精度要求。一旦确定模型是ARIMA之后,还需要确定参数d的取值。在统计学中并没有严谨的方法论告诉我们应该如何选择参数d,但在数据被输入ARIMA之前、该数据应该已经经过了多步差分、满足了平稳性条件。因此ARIMA模型中的d是锦上添花、可以帮助我们使用复合的差分运算来提升模型精度,但不是绝对的必须项。因此d可以为0,在不为0的时候,d也是1、2、3这样较小的阶数。
在选择参数d时,往往从1、2、3阶中选择方差最小、差分后数据噪音程度较低的阶数,尽量避免过差分。我们也可以对进行差分后的数据绘制ACF图像,如果滞后为1时ACF为负数(如下图),那大概率说明此时的高阶差分会导致过差分。
最后,再来看看实践中容易出现的几个问题:
-
是否会出现ACF和PACF都拖尾、不截尾的情况?
几乎不会出现,如果是这样的情况,可以尝试先保证时间序列平稳后再绘制ACF和PACF。
-
如果ACF或PACF拖尾,但另一个指标不截尾(比如,没有任何滞后对应的值显著),无法选择p或q的值怎么办?
同样的,尝试令序列平稳后再绘制ACF和PACF。如果依然出现相同的情况,考虑使用[1,3]之间的正整数进行尝试。如果尝试失败,则考虑直接升级为ARIMA模型。
-
如果ACF或PACF中出现多个显著的值,如何选择截断处?
5.2 时间序列的评估指标
大部分时候,我们可以使用回归模型的评估指标来评估时序模型(例如,MSE或MAE),但在对时序模型进行选择时,我们往往使用统计学中常见的模型质量评估指标赤池信息准则(Akaike Information Criterion,AIC)、贝叶斯信息准则(Bayesian Information Criterion,BIC)、汉南-奎因信息准则(Hannan–Quinn information criterion,HQIC)等。这些“信息准则”可以被用于衡量时间序列模型的优秀程度,其中最常用的AIC的计算公式如下:
A I C = − 2 l n ( L ) + 2 k AIC=-2ln(L)+2k AIC=−2ln(L)+2k
可以被认为是当前模型的积极性评估指标(即模型越好、该评估指标越高),大部分情况下我们使用的是统计学模型的极大似然估计结果(MLE,Maximum Likelihood Estimation),则代表该模型中需要被估计的参数量,而的底数为自然底数。
极大似然估计是不同于最小二乘的另一类参数估计方式,最小二乘法的目标是找出令损失函数最小的参数群,而极大似然估计的目标是找出最能描述当前数据的概率分布的参数群。在分类任务中,对极大似然估计的结果取负对数来做损失,从而得到著名的二分类损失函数logloss。在时间序列中,同样也对极大似然估计的结果取负对数,以此来得到越小越好的AIC。
不难发现,当越大时ln(L)越大,因此−2()就会越小。而对任意模型而言,参数量越少则代表模型越优越,因此当前模型质量越高、效率越高,AIC越小。在实际使用中,往往使用AIC判断多个模型中的哪一个最有可能成为给定数据的最佳模型,因此AIC要在有比较的情况下才能使用,当然这种比较可以是不同的模型、也可以是相同的模型、但不同超参数设置下的比较。对时间序列,AIC能够轻松地在测试集上测试模型性能。在统计学当中,对时序模型,几乎会100%地使用AIC作为模型选择时依赖的指标。
BIC与AIC非常相似,它对模型参数量的惩罚高于AIC,因此BIC也是越低越好,经常和AIC一起组合使用。HQIC平时使用不多,但同样作为越低越好的指标,当模型的AIC和BIC高度相似时,我们可能会对比HQIC的值来评估模型。
需要注意的是,时间序列模型的评估指标和机器学习模型的评估指标类似,它们只能反馈当前模型的精度,无法反馈模型的泛化能力。因此在许多统计学库、机器学习库中,我们可能追求最小的AIC,但同时也需要时序交叉验证的帮助来证明模型的泛化能力。如果数据量很小,无法完成交叉验证,那当前模型的整体泛化能力可能是值得怀疑的。但相反,如果一个模型在AIC很低的同时,还能够通过统计学中各种复杂的检验,那模型的泛化能力是可以被认可的。
HQIC平时使用不多,但同样作为越低越好的指标,当模型的AIC和BIC高度相似时,我们可能会对比HQIC的值来评估模型。
需要注意的是,时间序列模型的评估指标和机器学习模型的评估指标类似,它们只能反馈当前模型的精度,无法反馈模型的泛化能力。因此在许多统计学库、机器学习库中,我们可能追求最小的AIC,但同时也需要时序交叉验证的帮助来证明模型的泛化能力。如果数据量很小,无法完成交叉验证,那当前模型的整体泛化能力可能是值得怀疑的。但相反,如果一个模型在AIC很低的同时,还能够通过统计学中各种复杂的检验,那模型的泛化能力是可以被认可的。