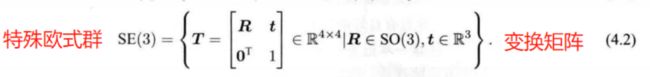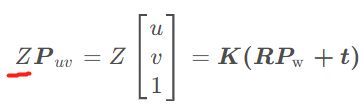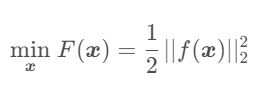《视觉 SLAM 十四讲》V2 第 6 讲 非线性优化 【高斯牛顿法、列文伯格-马夸尔特方法 、Ceres 库 和 g2o库 】
文章目录
-
-
- 6.1.2 最小二乘
- 寻找下降增量 Δ x k \Delta\bm{x}_k Δxk的 4 种方法
-
- 6.2.1 一阶和二阶梯度法(最速下降法、牛顿法)
- 6.2.2 高斯牛顿法
- 6.2.3 列文伯格-马夸尔特方法 【阻尼牛顿法】【信赖区域法】
- 6.3 实践
-
- 6.3.1 手写高斯牛顿法 【Code】
- 6.3.2 谷歌的优化库 Ceres 【最小二乘问题求解库】【Code】
- 6.3.3 g2o(General Graphic Optimization) 【Code】
- 习题
-
- √ 题1
- 题2
- 题3
- 题4
- LaTex
-
最小二乘法
下降策略: 高斯牛顿法、列文伯格-马夸尔特方法
Ceres库 和 g2o 库
如何在 有噪声的数据 中进行准确的 状态估计
——————
6.1 状态估计问题
假设在 x k \bm{x}_k xk 处 对 路标 y j \bm{y}_j yj 进行了一次观测, 对应到图像上的 像素坐标 为 z k , j \bm{z}_{k, j} zk,j,
则观测方程可表示为: s z k , j = K ( R k y j + t k ) s\bm{z}_{k, j} = \bm{K}(\bm{R}_k\bm{y}_j+\bm{t}_k) szk,j=K(Rkyj+tk)
其中 K \bm{K} K 为相机内参,s为像素点的距离(??),也是 ( R k y j + t k ) (\bm{R}_k\bm{y}_j+\bm{t}_k) (Rkyj+tk) 的第三个分量。
数据 受 噪声 影响后的变化
在运动和观测方程中,通常假设两个噪声项 w k , v k , j \bm{w}_k, \bm{v}_{k,j} wk,vk,j 满足零均值的高斯分布:
w k ∼ N ( 0 , R k ) , v k ∼ N ( 0 , Q k , j ) \bm{w}_k \sim \mathcal{N}(\bm{0}, \bm{R}_k),\bm{v}_k \sim \mathcal{N}(\bm{0}, \bm{Q}_{k,j}) wk∼N(0,Rk),vk∼N(0,Qk,j)
状态估计问题: 通过带噪声的数据 z \bm{z} z 和 u \bm{u} u 推断位姿 x \bm{x} x 和 地图 y \bm{y} y (以及它们的概率分布)。
处理这个状态估计问题的两种方法:
1、增量/渐进(incremental)【滤波器】
- 持有一个当前时刻的估计状态,然后用新的时刻来更新它。【仅关心当前时刻的状态估计 x k \bm{x}_k xk】
- 扩展卡尔曼滤波器
2、
批量(batch)方法
- 把数据 “攒” 起来 一并处理。
- 可以在更大的范围达到最优化, 非实时
————————
折中办法
滑动窗口估计法: 固定一些历史轨迹,仅对当前时刻附近的一些轨迹进行优化。
以非线性优化为主的批量优化方法
考虑从 1 到 N N N 的所有时刻,假设有 M M M 个路标点。
定义所有时刻的机器人位姿和路标点坐标为:
x = { x 1 , ⋅ ⋅ ⋅ , x N } , y = { y 1 , ⋅ ⋅ ⋅ , y M } \bm{x} = \{\bm{x}_1,···,\bm{x}_N\},\bm{y} = \{\bm{y}_1,···,\bm{y}_M\} x={x1,⋅⋅⋅,xN},y={y1,⋅⋅⋅,yM}
用不带下标的 u \bm{u} u 表示所有时刻的输入, z \bm{z} z 表示所有时刻的观测数据。
估计 机器人 状态 <==>已知输入数据 u \bm{u} u 和观测数据 z \bm{z} z 的条件下,求状态 x , y \bm{x, y} x,y 的条件概率分布 P ( x , y ∣ z , u ) P(\bm{x},\bm{y}|\bm{z}, \bm{u}) P(x,y∣z,u)
————————
不知道控制输入,只有一张张图像,即只考虑观测方程带来的数据时,相当于估计 P ( x , y ∣ z ) P(\bm{x},\bm{y}|\bm{z}) P(x,y∣z) 的条件概率分布
SfM(Structure from Motion)问题, 即如何从许多图像中重建三维空间结构。
估计 状态变量 的条件分布
根据 贝叶斯法则:
后验概率 P ( x , y ∣ z , u ) = P ( z , u ∣ x , y ) P ( x , y ) P ( z , u ) ∝ P ( z , u ∣ x , y ) P ( x , y ) \begin{align*}后验概率 P(\bm{x},\bm{y}|\bm{z},\bm{u}) &= \frac{P(\bm{z},\bm{u}|\bm{x},\bm{y})P(\bm{x},\bm{y})}{P(\bm{z},\bm{u})}\\ &\propto P(\bm{z},\bm{u}|\bm{x},\bm{y})P(\bm{x},\bm{y})\end{align*} 后验概率P(x,y∣z,u)=P(z,u)P(z,u∣x,y)P(x,y)∝P(z,u∣x,y)P(x,y)
似然(Likehood): P ( z , u ∣ x , y ) P(\bm{z},\bm{u}|\bm{x},\bm{y}) P(z,u∣x,y)
先验(Prior): P ( x , y ) P(\bm{x},\bm{y}) P(x,y)
求解 最大 后验概率 等价于 最大化 似然 P ( z , u ∣ x , y ) P(\bm{z},\bm{u}|\bm{x},\bm{y}) P(z,u∣x,y) 和 先验 P ( x , y ) P(\bm{x},\bm{y}) P(x,y) 的乘积。
( x , y ) M A P ∗ = arg max P ( x , y ∣ z , u ) = arg max P ( z , u ∣ x , y ) P ( x , y ) (\bm{x},\bm{y})_\mathrm{MAP}^*=\arg \max P(\bm{x},\bm{y}|\bm{z},\bm{u}) = \arg\max P(\bm{z},\bm{u}|\bm{x},\bm{y})P(\bm{x},\bm{y}) (x,y)MAP∗=argmaxP(x,y∣z,u)=argmaxP(z,u∣x,y)P(x,y)
不知道 机器人位姿 或 路标 大概在什么地方,没有了先验。 即 P ( x , y ) P(\bm{x},\bm{y}) P(x,y) 不知道。
此时求解最大似然估计(Maximize Likelihood Estimation, MLE):
( x , y ) M L E ∗ = arg max P ( z , u ∣ x , y ) (\bm{x},\bm{y})_\mathrm{MLE}^*=\arg \max P(\bm{z},\bm{u}|\bm{x},\bm{y}) (x,y)MLE∗=argmaxP(z,u∣x,y)
似然 P ( z , u ∣ x , y ) P(\bm{z},\bm{u}|\bm{x},\bm{y}) P(z,u∣x,y): 在现在的位姿下,可能产生怎样的观测数据。
最大似然估计 ( x , y ) M L E ∗ (\bm{x},\bm{y})_\mathrm{MLE}^* (x,y)MLE∗: 在什么样的状态下,最可能产生现在观测到的数据。
6.1.2 最小二乘
如何求最大似然估计?
对于某一次观测 z k , j = h ( y j , x k ) + v k . j \bm{z}_{k, j}=h(\bm{y}_j,\bm{x}_k)+\bm{v}_{k.j} zk,j=h(yj,xk)+vk.j
设噪声项 v k ∼ N ( 0 , Q k , j ) \bm{v}_k \sim \mathcal{N}(\bm{0}, \bm{Q}_{k,j}) vk∼N(0,Qk,j)
观测数据的条件概率为:
P ( z j , k ∣ x k , y j ) = N ( h ( y j , x k ) , Q k , j ) P(\bm{z}_{j,k}|\bm{x}_k,\bm{y}_j)=N(h(\bm{y}_j,\bm{x}_k),\bm{Q}_{k,j}) P(zj,k∣xk,yj)=N(h(yj,xk),Qk,j)



稀疏性:运动误差只与 x k − 1 , x k \bm{x}_{k-1}, \bm{x}_k xk−1,xk有关,观测误差只与 x k , y j \bm{x}_{k}, \bm{y}_j xk,yj 有关。【为啥呢?】
用李代数表示增量,是无约束的最小二乘问题
用旋转矩阵/变换矩阵描述位姿,需要引入旋转矩阵自身的约束【须满足 R R T = I \bm{R}\bm{R}^T=\bm{I} RRT=I 且 d e t ( R det(\bm{R} det(R) = 1】
如何求解这个最小二乘问题?
6.1.3 例子:批量状态估计
下面的 Q 和 R 似乎反了。
对于一辆沿 x x x 轴前进 或 后退的汽车
设 u k \bm{u}_k uk 为输入, w k \bm{w}_k wk 为噪声,取时间为 k = 1 , 2 , 3 k = 1, 2,3 k=1,2,3
运动方程为: x k = x k − 1 + u k + w k \bm{x}_k=\bm{x}_{k-1}+\bm{u}_k+\bm{w}_k xk=xk−1+uk+wk, w k ∼ N ( 0 , Q k ) \bm{w}_k\sim \mathcal{N}(0, \bm{Q}_k) wk∼N(0,Qk)
设 z k \bm{z}_k zk 为对汽车位置的测量
观测方程为: z k = x k + n k \bm{z}_k=\bm{x}_{k}+\bm{n}_k zk=xk+nk, n k ∼ N ( 0 , R k ) \bm{n}_k\sim \mathcal{N}(0, \bm{R}_k) nk∼N(0,Rk)
根据已有的 v \bm{v} v, y \bm{y} y 进行状态估计
设初始状态 x 0 \bm{x}_0 x0 已知
推导 批量状态 的最大似然估计
令批量状态变量为 x = [ x 0 , x 1 , x 2 , x 3 ] T \bm{x} = [\bm{x}_0,\bm{x}_1,\bm{x}_2,\bm{x}_3]^T x=[x0,x1,x2,x3]T
令批量观测为 z = [ z 1 , z 2 , z 3 ] T \bm{z} = [\bm{z}_1,\bm{z}_2,\bm{z}_3]^T z=[z1,z2,z3]T
令批量输入变量为 u = [ u 1 , u 2 , u 3 ] T \bm{u} = [\bm{u}_1,\bm{u}_2,\bm{u}_3]^T u=[u1,u2,u3]T
最大似然估计为:
x m a p ∗ = arg max P ( x ∣ u , z ) = arg max P ( u , z ∣ x ) = ∏ k = 1 3 P ( u k ∣ x k − 1 , x k ) ∏ k = 1 3 P ( z k ∣ x k ) \begin{align*}\bm{x}_\mathrm{map}^* &= \arg\max P(\bm{x}|\bm{u}, \bm{z})\\ &= \arg\max P(\bm{u}, \bm{z}|\bm{x})\\ &= \prod\limits_{k=1}^3P(\bm{u}_k|\bm{x}_{k-1},\bm{x}_k)\prod\limits_{k=1}^3P(\bm{z}_k|\bm{x}_k)\end{align*} xmap∗=argmaxP(x∣u,z)=argmaxP(u,z∣x)=k=1∏3P(uk∣xk−1,xk)k=1∏3P(zk∣xk)
其中
P ( u k ∣ x k − 1 , x k ) = N ( x k − x k − 1 , Q k ) P(\bm{u}_k|\bm{x}_{k-1},\bm{x}_k)=\mathcal{N}(\bm{x}_k-\bm{x}_{k-1},\bm{Q}_k) P(uk∣xk−1,xk)=N(xk−xk−1,Qk)
P ( z k ∣ x k ) = N ( x k , R k ) P(\bm{z}_k|\bm{x}_k)=\mathcal{N}(\bm{x}_k,\bm{R}_k) P(zk∣xk)=N(xk,Rk)
构建误差变量:
e u , k = x k − x k − 1 − u k e z , k = z k − x k \begin{align*}\bm{e}_{\bm{u},k} &= \bm{x}_k-\bm{x}_{k-1}-\bm{u}_k\\ \bm{e}_{\bm{z},k}&=\bm{z}_k-\bm{x}_k\end{align*} eu,kez,k=xk−xk−1−uk=zk−xk
最小二乘的目标函数为:
min ∑ k = 1 3 e u , k T Q k − 1 e u , k + ∑ k = 1 3 e z , k T R k − 1 e z , k \min\sum\limits_{k=1}^{3}\bm{e}_{\bm{u},k}^T\bm{Q}_k^{-1}\bm{e}_{\bm{u},k} + \sum\limits_{k=1}^{3}\bm{e}_{\bm{z},k}^T\bm{R}_k^{-1}\bm{e}_{\bm{z},k} mink=1∑3eu,kTQk−1eu,k+k=1∑3ez,kTRk−1ez,k
——————
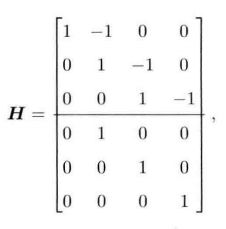
令 y = [ u , z ] T \bm{y}=[\bm{u}, \bm{z}]^T y=[u,z]T
y − H x = e ∼ N ( 0 , Σ ) \bm{y-Hx=e} \sim \mathcal{N}(\bm{0},\bm{\Sigma}) y−Hx=e∼N(0,Σ)
Σ = d i a g ( Q 1 , Q 2 , Q 3 , R 1 , R 2 , R 3 ) \Sigma=\mathrm{diag}(\bm{Q}_1,\bm{Q}_2,\bm{Q}_3,\bm{R}_1,\bm{R}_2,\bm{R}_3) Σ=diag(Q1,Q2,Q3,R1,R2,R3)
x m a p ∗ = arg max e T Σ − 1 e \bm{x}_\mathrm{map}^* = \arg\max \bm{e}^T\bm{\Sigma}^{-1}\bm{e} xmap∗=argmaxeTΣ−1e
有唯一解: x m a p ∗ = ( H T Σ − 1 H ) − 1 H T Σ − 1 y \bm{x}_\mathrm{map}^* = ({\bm{H}^{T}\bm{\Sigma}^{-1}}\bm{H})^{-1}\bm{H}^{T}\bm{\Sigma}^{-1}\bm{y} xmap∗=(HTΣ−1H)−1HTΣ−1y
寻找下降增量 Δ x k \Delta\bm{x}_k Δxk的 4 种方法
6.2 非线性最小二乘
求解一个简单的最小二乘问题:
min x F ( x ) = 1 2 ∣ ∣ f ( x ) ∣ ∣ 2 2 \min\limits_{\bm{x}}F(\bm{x})=\frac{1}{2}||f(\bm{x})||_2^2 xminF(x)=21∣∣f(x)∣∣22
d F d x = 0 \frac{dF}{d\bm{x}}=\bm{0} dxdF=0
得到 导数为0处的极值,可能为极大、极小或鞍点
不足: 需要知道目标函数的全局性质;求解不易
——> 迭代 【求解导数为0 ——> 不断寻找下降增量 Δ x k \Delta\bm{x}_k Δxk】
如何寻找这个增量 Δ x k \Delta\bm{x}_k Δxk?
方法:一阶梯度或二阶梯度法(最速下降法、牛顿法)、高斯牛顿法、列文伯格—马夸尔特方法
6.2.1 一阶和二阶梯度法(最速下降法、牛顿法)
将目标函数在 x k \bm{x}_k xk 附近进行泰勒展开
F ( x k + Δ x k ) ≈ F ( x k ) + J ( x k ) T Δ x k + 1 2 Δ x k T H ( x k ) Δ x k F(\bm{x}_k+\Delta\bm{x}_k) \approx F(\bm{x}_k) + \bm{J}(\bm{x}_k)^T\Delta\bm{x}_k+\frac{1}{2}\Delta\bm{x}_k^T\bm{H}(\bm{x}_k)\Delta\bm{x}_k F(xk+Δxk)≈F(xk)+J(xk)TΔxk+21ΔxkTH(xk)ΔxkJ ( x k ) \bm{J}(\bm{x}_k) J(xk): F ( x k ) F(\bm{x}_k) F(xk)关于\bm{x} 的一阶导数 【梯度、雅可比(Jacobian)矩阵)】
H \bm{H} H: 二阶导数 【海塞(Hessian)矩阵】
一阶梯度或二阶梯度法:仅保留 泰勒展开 的一阶或二阶项
最速下降法: 取增量为一阶梯度的反向【 Δ x ∗ = − J ( x k ) \Delta\bm{x}^*=-\bm{J}(\bm{x}_k) Δx∗=−J(xk)】,再指定一个步长 λ \lambda λ
——————
保留二阶梯度信息
Δ x ∗ = arg min ( F ( x ) + J ( x ) T Δ x + 1 2 Δ x T H Δ x ) \Delta\bm{x}^*=\arg\min(F(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x}+\frac{1}{2}\Delta\bm{x}^T\bm{H}\Delta\bm{x}) Δx∗=argmin(F(x)+J(x)TΔx+21ΔxTHΔx)
J + H Δ x = 0 \bm{J} + \bm{H}\Delta\bm{x}=\bm{0} J+HΔx=0
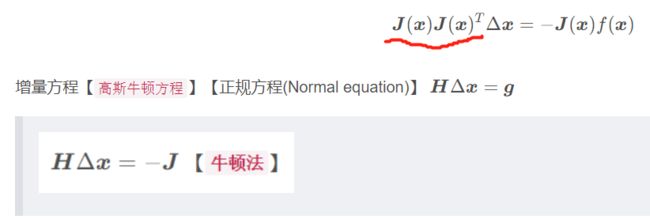
H Δ x = − J \bm{H}\Delta\bm{x}=-\bm{J} HΔx=−J 【牛顿法】
——————
一阶二阶梯度法
- 直观,把函数在迭代点附近进行泰勒展开,并针对更新量做最小化即可。
- 用一个一次或二次的函数近似原函数,用近似函数的最小值来猜测原函数的极小值。
最速下降法: 过于贪心,容易走出锯齿路线,增加迭代次数
牛顿法
- 需要计算目标函数的 H \bm{H} H 矩阵,规模大时计算困难
————————
对于最小二乘问题,更实用的方法: 高斯牛顿法 和 列文伯格—马夸尔特方法。
6.2.2 高斯牛顿法
思想:将 f ( x ) f(\bm{x}) f(x) 进行一阶的泰勒展开。
牛顿法 展开的是 F ( x ) F(\bm{x}) F(x)
F ( x + Δ x ) ≈ F ( x ) + J ( x ) T Δ x + 1 2 Δ x T H Δ x F(\bm{x}+\Delta\bm{x}) \approx F(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x}+\frac{1}{2}\Delta\bm{x}^T\bm{H}\Delta\bm{x} F(x+Δx)≈F(x)+J(x)TΔx+21ΔxTHΔx
f ( x + Δ x ) ≈ f ( x ) + J ( x ) T Δ x f(\bm{x}+\Delta\bm{x}) \approx f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x} f(x+Δx)≈f(x)+J(x)TΔx
其中 J ( x ) T \bm{J}(\bm{x})^T J(x)T 为 f ( x ) f(\bm{x}) f(x) 关于 x \bm{x} x 的导数,为 n × 1 n\times1 n×1 的列向量。
寻找增量 Δ x \Delta\bm{x} Δx ,使得 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 ||f(\bm{x}+\Delta\bm{x})||^2 ∣∣f(x+Δx)∣∣2 达到最小。
——> 解一个线性的最小二乘问题:
Δ x ∗ = arg min Δ x 1 2 ∣ ∣ f ( x ) + J ( x ) T Δ x ∣ ∣ 2 \Delta\bm{x}^* = \arg\min\limits_{\Delta\bm{x}}\frac{1}{2}||f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x}||^2 Δx∗=argΔxmin21∣∣f(x)+J(x)TΔx∣∣2
将上述目标函数对 Δ x \Delta\bm{x} Δx 求导,并令导数为零。
1 2 ∣ ∣ f ( x ) + J ( x ) T Δ x ∣ ∣ 2 = 1 2 ( f ( x ) + J ( x ) T Δ x ) T ( f ( x ) + J ( x ) T Δ x ) = 1 2 ( f ( x ) T + Δ x T J ( x ) ) ( f ( x ) + J ( x ) T Δ x ) = 1 2 ( ∣ ∣ f ( x ) ∣ ∣ 2 + f ( x ) T J ( x ) T Δ x + Δ x T J ( x ) f ( x ) + Δ x T J ( x ) J ( x ) T Δ x ) \begin{align*}\frac{1}{2}||f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x}||^2&=\frac{1}{2}(f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x})^T(f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x})\\ &=\frac{1}{2}(f(\bm{x})^T + \Delta\bm{x}^T\bm{J}(\bm{x}))(f(\bm{x}) + \bm{J}(\bm{x})^T\Delta\bm{x})\\ &= \frac{1}{2}(||f(\bm{x})||^2+f(\bm{x})^T\bm{J}(\bm{x})^T\Delta\bm{x}+ \Delta\bm{x}^T\bm{J}(\bm{x})f(\bm{x})+\Delta\bm{x}^T\bm{J}(\bm{x})\bm{J}(\bm{x})^T\Delta\bm{x} ) \\ \end{align*} 21∣∣f(x)+J(x)TΔx∣∣2=21(f(x)+J(x)TΔx)T(f(x)+J(x)TΔx)=21(f(x)T+ΔxTJ(x))(f(x)+J(x)TΔx)=21(∣∣f(x)∣∣2+f(x)TJ(x)TΔx+ΔxTJ(x)f(x)+ΔxTJ(x)J(x)TΔx)
求导
( f ( x ) T J ( x ) T ) T + J ( x ) f ( x ) + ( J ( x ) J ( x ) T ) T Δ x + J ( x ) J ( x ) T Δ x = 0 (f(\bm{x})^T\bm{J}(\bm{x})^T)^T+\bm{J}(\bm{x})f(\bm{x}) + (\bm{J}(\bm{x})\bm{J}(\bm{x})^T)^T\Delta\bm{x} + \bm{J}(\bm{x})\bm{J}(\bm{x})^T\Delta\bm{x} =0 (f(x)TJ(x)T)T+J(x)f(x)+(J(x)J(x)T)TΔx+J(x)J(x)TΔx=0
J ( x ) f ( x ) + J ( x ) J ( x ) T Δ x = 0 \bm{J}(\bm{x})f(\bm{x}) + \bm{J}(\bm{x})\bm{J}(\bm{x})^T\Delta\bm{x} =0 J(x)f(x)+J(x)J(x)TΔx=0
J ( x ) J ( x ) T Δ x = − J ( x ) f ( x ) \bm{J}(\bm{x})\bm{J}(\bm{x})^T\Delta\bm{x} =-\bm{J}(\bm{x})f(\bm{x}) J(x)J(x)TΔx=−J(x)f(x)
增量方程【高斯牛顿方程】【正规方程(Normal equation)】 H Δ x = g \bm{H}\Delta \bm{x}=\bm{g} HΔx=g
高斯牛顿法 用 J J T \bm{JJ}^T JJT 作为 牛顿法 中 二阶 Hessian 矩阵的近似。
不足:
1、为了求解 增量方程,需要求解 H − 1 \bm{H}^{-1} H−1 ,需要矩阵 H \bm{H} H 可逆,可能出现 J J T \bm{JJ}^T JJT 为奇异矩阵的情况,导致算法不收敛。
2、若是步长 Δ x \Delta\bm{x} Δx 太大,会导致局部近似式 (6.30) 不够准确。
- 即 高斯牛顿法 采用的近似二阶泰勒展开只能在 展开点附近 有较好的 近似效果。
6.2.3 列文伯格-马夸尔特方法 【阻尼牛顿法】【信赖区域法】
修正了 高斯牛顿法的上述不足,但收敛速度比高斯牛顿法慢,被称为阻尼牛顿法(Damped Newton Method)
高斯牛顿法 采用的近似二阶泰勒展开只能在 展开点附近 有较好的 近似效果。
——> 给 Δ x \Delta\bm{x} Δx 添加一个范围 信赖区域
如何确定这个信赖区域的范围?
比较 近似模型 和 实际函数 之间的差异



带 不等式约束 的优化问题,用拉格朗日乘子 把 约束项 放到目标函数中,构成拉格朗日函数:

当参数 λ \lambda λ 较小,接近高斯牛顿方法
当参数 λ \lambda λ 较大,更接近一阶梯度下降法(最速下降)
问题性质较好——> 高斯牛顿法
问题接近病态——> 列文伯格-马夸尔特方法
——————
非线性优化的通病:变量的初始值对于优化效果影响较大,容易陷入局部极小值。
视觉SLAM: 用ICP、PnP 之类的算法 提供优化初始值。
6.3 实践
6.3.1 手写高斯牛顿法 【Code】
cmake_minimum_required(VERSION 2.8)
project(ch6)
set(CMAKE_CXX_STANDARD 17) ## 新版 g2o库 需要
set(CMAKE_BUILD_TYPE Release)
set(CMAKE_CXX_FLAGS "-std=c++14 -O3")
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
# OpenCV
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})
# Ceres
find_package(Ceres REQUIRED)
include_directories(${CERES_INCLUDE_DIRS})
# g2o
find_package(G2O REQUIRED)
include_directories(${G2O_INCLUDE_DIRS})
# Eigen
include_directories("/usr/include/eigen3")
add_executable(gaussNewton gaussNewton.cpp)
target_link_libraries(gaussNewton ${OpenCV_LIBS})
add_executable(ceresCurveFitting ceresCurveFitting.cpp)
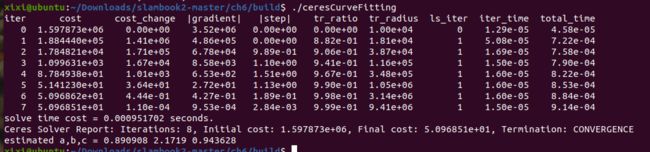
target_link_libraries(ceresCurveFitting ${OpenCV_LIBS} ${CERES_LIBRARIES})
add_executable(g2oCurveFitting g2oCurveFitting.cpp) # g2o部分 若是 新版g2o库 需要修改 源代码
target_link_libraries(g2oCurveFitting ${OpenCV_LIBS} ${G2O_CORE_LIBRARY} ${G2O_STUFF_LIBRARY})
gaussNewton.cpp
#include 6.3.2 谷歌的优化库 Ceres 【最小二乘问题求解库】【Code】
//
// Created by xiang on 18-11-19.
//
#include 6.3.3 g2o(General Graphic Optimization) 【Code】
g2o(General Graphic Optimization, G 2 O \mathrm{G^2O} G2O)
结点: 优化变量
边: 误差项
基于 图优化
// 构建图优化,先设定g2o
/*typedef g2o::BlockSolver> BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1
typedef g2o::LinearSolverDense LinearSolverType; // 线性求解器类型
*/
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver
(new g2o::LinearSolverDense<g2o::BlockSolverX::PoseMatrixType>());
// 梯度下降方法,可以从GN, LM, DogLeg 中选
/*auto solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique(g2o::make_unique()));*/
std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton(std::move(solver_ptr));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
/usr/local/include/g2o/stuff/tuple_tools.h:41:46: error: ‘tuple_size_v’ is not a member of ‘std’; did you mean ‘tuple_size’?
41 | f, t, i, std::make_index_sequence<std::tuple_size_v<std::decay_t<T>>>());
解决办法:
在 CMakeLists.txt 中添加 set(CMAKE_CXX_STANDARD 17)
——————————————
g2oCurveFitting.cpp
#include > BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1
typedef g2o::LinearSolverDense LinearSolverType; // 线性求解器类型
*/
std::unique_ptr<g2o::BlockSolverX::LinearSolverType> linearSolver
(new g2o::LinearSolverDense<g2o::BlockSolverX::PoseMatrixType>());
// 梯度下降方法,可以从GN, LM, DogLeg 中选
/*auto solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique(g2o::make_unique()));*/
std::unique_ptr<g2o::BlockSolverX> solver_ptr (new g2o::BlockSolverX(std::move(linearSolver)));
g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton(std::move(solver_ptr));
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 往图中增加顶点
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae, be, ce));
v->setId(0);
optimizer.addVertex(v);
// 往图中增加边
for (int i = 0; i < N; i++) {
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge(edge);
}
// 执行优化
cout << "start optimization" << endl;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(10);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
cout << "solve time cost = " << time_used.count() << " seconds. " << endl;
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
cout << "estimated model: " << abc_estimate.transpose() << endl;
return 0;
}

每次的运行时间都不太一样
直觉上:
![]()
——————
6.4 小结
SLAM中经常遇到的一种非线性优化问题:由许多个误差项平方和组成的最小二乘问题。
实践部分: 手写高斯牛顿法、Ceres 和 g2o 库 求解同一个曲线拟合问题。
g2o 提供了大量现成的顶点和边,非常便于相机位姿估计问题。
习题
√ 题1
1、 证明线性方程 A x = b \bm{Ax = b} Ax=b 当系数矩阵 A \bm{A} A 超定时,最小二乘解为 x = ( A T A ) − 1 A T b \bm{x}=(\bm{A}^T\bm{A})^{-1}\bm{A}^T\bm{b} x=(ATA)−1ATb。
当 方程数 多于 未知数个数时,也就是说对应系数矩阵的行数大于列数【系数矩阵 A \bm{A} A 超定】,这样的方程组称为超定方程组。
方程个数比未知数个数多,不同方程之间会发生"冲突",导致整个方程组没有精确解。但可以设定一个误差标准,找到一个让这个误差标准值最小的近似解。
所以本题可以理解为:针对无精确解的方程组 A x = b \bm{Ax = b} Ax=b ,利用最小二乘误差标准求解其近似值。
求解最小二乘问题:
x ∗ = arg min x 1 2 ∣ ∣ f ( x ) ∣ ∣ 2 \bm{x}^* = \arg\min\limits_{\bm{x}}\frac{1}{2}||f(\bm{x})||^2 x∗=argxmin21∣∣f(x)∣∣2
本题中
1 2 ∣ ∣ f ( x ) ∣ ∣ 2 = 1 2 ( A x − b ) T ( A x − b ) = 1 2 ( x T A T − b T ) ( A x − b ) = 1 2 ( x T A T A x − b T A x − x T A T b + b T b ) \begin{align*}\frac{1}{2}||f(\bm{x})||^2 &=\frac{1}{2}(\bm{Ax - b})^T(\bm{Ax - b})\\ &=\frac{1}{2}(\bm{x}^T\bm{A}^T - \bm{b}^T)(\bm{Ax - b})\\ &=\frac{1}{2}(\bm{x}^T\bm{A}^T\bm{Ax} - \bm{b}^T\bm{Ax}-\bm{x}^T\bm{A}^T \bm{b}+\bm{b}^T\bm{b})\end{align*} 21∣∣f(x)∣∣2=21(Ax−b)T(Ax−b)=21(xTAT−bT)(Ax−b)=21(xTATAx−bTAx−xTATb+bTb)
上式对 x \bm{x} x 求导并令其为0
( A T A ) T x + A T A x − ( b T A ) T − A T b = 0 (\bm{A}^T\bm{A})^T\bm{x}+\bm{A}^T\bm{Ax}-(\bm{b}^T\bm{A})^T-\bm{A}^T \bm{b} =0 (ATA)Tx+ATAx−(bTA)T−ATb=0
A T A x = A T b \bm{A}^T\bm{Ax}=\bm{A}^T \bm{b} ATAx=ATb
x = ( A T A ) − 1 A T b \bm{x}= (\bm{A}^T\bm{A})^{-1}\bm{A}^T\bm{b} x=(ATA)−1ATb
证毕。
其它解法链接
题2
2、调研最速下降法、牛顿法、高斯牛顿法 和 列文伯格-马夸尔特方法各有什么优缺点。除了我们举的Ceres 库和g2o 库,还有哪些常用的优化库?你可能会找到一些MATLAB 上的库。


优化库:
GTSAM(https://gtsam.org/) GTSAM是一个开源的因子图优化库,使用C++实现。它提供了一系列的因子和变量类型,包括了视觉、IMU、GNSS和路标等因子和位姿、速度、IMU偏差和路标等变量。GTSAM还提供了多种优化器,并支持基于纯图的优化和基于混合图的优化。GTSAM有很多应用案例和文档,使用起来相对较易。
题3
3、为什么高斯牛顿法的增量方程系数矩阵可能不正定?不正定有什么几何含义?为什么在这种情况下解就不稳定了?



题4
4、DogLeg 是什么?它与 高斯牛顿法 和 列文伯格-马夸尔特方法 有何异同?
- 整理PPT
参考链接-P18
Dogleg属于Trust Region优化方法,即用置信域的方法在最速下降法和高斯牛顿法之间进行切换(将二者的搜索步长及方向转化为向量,两个向量进行叠加得到新的方向和置信域内的步长),相当于是一种加权求解。

——————————————————————————————————
LaTex
$\sim$
∼ \sim ∼
$\mathcal{N}$
N \mathcal{N} N
$\iff$
⟺ \iff ⟺
$\propto$
∝ \propto ∝
$\Sigma$
Σ \Sigma Σ