阻抗控制与导纳控制

引言

无论是阻抗控制还是导纳控制，寻求的均是力与位置之间的对应关系，模拟二阶阻尼系统，如下式，本文主要以笛卡尔空间控制为例
$$M{\ddot{x}}_e+B{\dot{x}}_e+K{x}_e=F_e\text{\hspace{1em}(1)}$$
式中，$F_e$表示机器人受到外界作用力，对应的$x_e=x-x_d$表示，这里简单解释下该对应关系

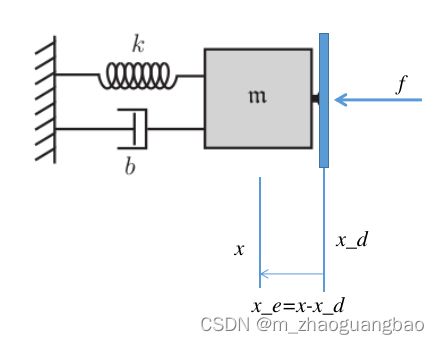
如图所示，假设f直接作用的蓝色板子为无质量物体，如图$x_e=x-x_d$，根据MBK各个部分对蓝色板子的作用力平衡可得到上式，这里的f为作用在系统上的作用力，故当$F_e$表示机器人受到外界作用力，对应的$x_e=x-x_d$表示。参考笛卡尔空间期望运动为：$x_d,\dot{x_d},\ddot{x_d}$。
机器人动力学模型
$$H(q)\ddot{q}+C(q,\dot{q})\dot{q}+g(q)=J^{T}f+\tau$$
式中，f表示机器人受到外界作用力（即$F_e$），等式右边为关节上作用扭矩，其中包括驱动器输出扭矩$\tau$和外力作用在关节上的作用力$J^{T}f$
由期望笛卡尔运动计算驱动器扭矩，由$\dot{x_d}=J\dot{q}$得：
$$\ddot{q}=J^{+}(\ddot{x_d}-\dot{J}\dot{q})$$
代入可得
$$\tau =H(q)J^{+}(\ddot{x_d}-\dot{J}\dot{q})+C(q,\dot{q})\dot{q}+g(q)-J^{T}f\text{\hspace{1em}(2)}$$

导纳控制

根据腕部力传感器测量外界对机械臂作用力，故f已知，获得期望的运动，根据(1)
$$\ddot{x}=M^{-1}（f-K{x}_e-B\dot{x_e}）+\ddot{x_d}$$
若要实现上述期望$\ddot{x}$，根据(2)则可获得对应的驱动力矩
$$\tau =H(q)J^{+}(M^{-1}（f-K{x}_e-B\dot{x_e}）+\ddot{x_d}-\dot{J}\dot{q})+C(q,\dot{q})\dot{q}+g(q)-J^{T}f$$
根据力和二阶系统参数计算实际笛卡尔空间执行加速度，进而获得关节驱动力矩

阻抗控制

作用在机械臂上的外部作用力f不可测量，根据机器人实际位置和期望位置计算末端应该反馈的作用力，注意这里和上面作用力定义的方向不同，这里是机械臂末端作用给环境的作用力，注意这里面$-J^{T}f$的符号，这里的$x_e$定义同上
$$\tau =J^T(M{\ddot{x}}_e+B{\dot{x}}_e+K{x}_e)+H(q)J^{+}(\ddot{x_d}-\dot{J}\dot{q})+C(q,\dot{q})\dot{q}+g(q)$$
由于${\ddot{x}}_e$测量误差会很大，所以一般取惯量矩阵M为0，则该形式等价于PD控制器加前馈补偿，和一般轨迹跟踪比较，精确控制的刚度参数K会设置的比较大，所以刚度很高，在所以机械臂在静止状态时，很难通过施加外力来拖动机械臂；相应的阻抗控制模式下的刚度参数K设置的比较小，因此均有一定的柔顺性。

参考及相关文档

阻抗控制在平面二连杆机械臂上的实现本链接中最后有惯量补偿和无惯量补偿的例子很好的验证了前馈通道的重要性
机器人关节空间阻抗控制律是基于什么样的思想得到的？ 为什么跟机器人关节PD控制的公式一样参见李淼的回答

代码实现分析

这里结合阻抗控制在平面二连杆机械臂上的实现的代码理一下导纳控制和阻抗控制的实现
前面关于导纳控制的部分和常见的“感知力转换为位置量控制”有点区别，之所以出现了力矩的控制量是由于涉及了底层控制，而一般的导纳控制只需要计算出加速度的信息，后面根据实际机器人的控制接口选择是速度控制或者位置控制即可（导纳控制不需要考虑底层的控制部分，因此不需要对机器人系统进行建模）

动力学建模

拉格朗日动力学建模在数学上的推导会比较直观，有助于得到理论结果，牛顿欧拉动力学建模实现起来比较方便，由于二连杆机器人所以这里的建模采用的是拉格朗日方法，这里先简单回顾一下
系统动能
$$T=\frac{1}{2}{\dot{q}}^{T}M\dot{q}$$
由系统动能获得质量矩阵
$$\frac{\partial T}{\partial \dot{q}}=M\dot{q},\frac{d}{dt}(\frac{\partial T}{\partial \dot{q}})=M\ddot{q}+\dot{M}\dot{q}$$
∂ T ∂ q = 1 2 [ q ˙ T ∂ M ∂ q 1 q ˙ ⋮ q ˙ T ∂ M ∂ q n q ˙ ] \frac{\partial T}{\partial q}=\frac{1}{2}\left[\begin{array}{c} \dot{\boldsymbol{q}}^{T} \frac{\partial M}{\partial q_{1}} \dot{\boldsymbol{q}} \\ \vdots \\ \dot{\boldsymbol{q}}^{T} \frac{\partial M}{\partial q_{n}} \dot{\boldsymbol{q}} \end{array}\right] ∂q∂T​=21​ ​q˙​T∂q1​∂M​q˙​⋮q˙​T∂qn​∂M​q˙​​ ​
易得
$$C(q,\dot{q})\dot{q}=\dot{M}\dot{q}-\frac{\partial T}{\partial q},g(q)=\frac{\partial U}{\partial q}$$
动力学建模代码实现

pEk_ptheta1dot = jacobian(Ek,theta1dot);
M11 = jacobian(pEk_ptheta1dot,theta1dot);
M12 = jacobian(pEk_ptheta1dot,theta2dot);

M111 = jacobian(M11,theta1); M112 = jacobian(M11,theta2); M121 = jacobian(M12,theta1); M122 = jacobian(M12,theta2);
c1 =  jacobian(pEk_ptheta1dot,theta1)*theta1dot + jacobian(pEk_ptheta1dot,theta2)*theta2dot - jacobian(Ek,theta1);
G1 =  jacobian(Ep,theta1);
B1 =  c1 + G1;

dEk_dtheta2dot = jacobian(Lagrange,theta2dot); % 势能只是关于位置的函数
M21 = M12; % symmetric matrix
M22 = jacobian(dEk_dtheta2dot,theta2dot);
M221 = jacobian(M22,theta1); M222 = jacobian(M22,theta2);
c2 =  jacobian(dEk_dtheta2dot,theta1)*theta1dot + jacobian(dEk_dtheta2dot,theta2)*theta2dot - jacobian(Ek,theta2);
G2 =  jacobian(Ep,theta2);
B2 =  c2 + G2;

C11 = 1/2*M111*theta1dot + 1/2*M112*theta2dot;
C12 = 1/2*M112*theta1dot + (M122 - 1/2*M221)*theta2dot;
C21 = (M121-1/2*M112)*theta1dot + 1/2*M221*theta2dot;
C22 = 1/2*M221*theta1dot + 1/2*M222*theta2dot;

M = [M11 M12;M21 M22];
M = simplify(M);
C = [C11,C12;C21,C22];
C = simplify(C);
c = [c1;c2];
c = simplify(c);
G = [G1;G2];
G = simplify(G);
B = [B1;B2];
B = simplify(B);

% velidate c = C*qdot
simplify(c - C*[theta1dot;theta2dot])
% validate M_dot = C + C^T
M_vec = [M11;M21;M12;M22];
M_dot  = jacobian(M_vec,theta1)*theta1dot + jacobian(M_vec,theta2)*theta2dot;
M_dot = reshape(M_dot,2,2);
simplify(M_dot - C - C.')

阻抗控制

% FUNC(Impedance_Controller), xd: 期望位置，xee: 当前位置
tau_impedance = J.'*([kpx,0;0,kpy]*([xd;yd]-[xee;yee]) + [kdx,0;0,kdy]*([xdotd;ydotd]-[xeedot;yeedot]));
% ----
J =Geometric_Jacobian(x0(1:2),[l1;l2]);
dJ_dt = Geometric_Jacobian_Derivative(x0,[l1;l2]);
qdotdotref = J\(eearef - dJ_dt*x0(3:4));
Mass = Mass_Matrix(x0(1:2),[I1 I2 l1 l2 m1 m2 a1 a2 g]');
u = Impedance_Controller(x0,[l1;l2],[kpx;kpy;kdx;kdy],eeposref,eevref)...
    + Mass*qdotdotref...
    + Coriolis_Centrifugal_Torque(x0,[l1;l2;m1;m2;a1;a2;g])...
    + Gravity_Torque(x0(1:2),[l1;l2;m1;m2;a1;a2;g]);

从实现上可以看出就是PD+动力学前馈

速度控制的导纳控制

% FUNC(Impedance_Controller), xd: 期望位置，xee: 当前位置
tau_admittance = J.'*([kpx,0;0,kpy]*([xd;yd]-[xee;yee]) + [kdx,0;0,kdy]*([xdotd;ydotd]-[xeedot;yeedot]) + [fx;fy]);
acc_admittance = M\tau_admittance;%[mx,0;0,my]
% ----
qdot_admittance = qdot_admittance + (qdotdot_admittance)*dt;
qdotref  = J\eevref + qdot_admittance;            

位置控制的导纳控制

% FUNC(Impedance_Controller), xd: 期望位置，xee: 当前位置
tau_admittance = J.'*([kpx,0;0,kpy]*([xd;yd]-[xee;yee]) + [kdx,0;0,kdy]*([xdotd;ydotd]-[xeedot;yeedot]) + [fx;fy]);
acc_admittance = M\tau_admittance;%[mx,0;0,my]
% ----
q_admittance = q_admittance + qdot_admittance*dt +  1/2*qdotdot_admittance*dt^2;           
qdot_admittance = qdot_admittance + qdotdot_admittance*dt;
qref = Inverse_Kinematics(x0(1:2),eeposref,[l1 l2]) + q_admittance;