MATLAB数学建模 回归与内插

以下内容为个人笔记，部分图片来源于郭老师课件或课程截图。
笔记汇总：MATLAB基础教程
课程视频：MATLAB基础教程-台大郭彦甫（14课全-高清-含课件）

---

多项式曲线拟合

polyfit()

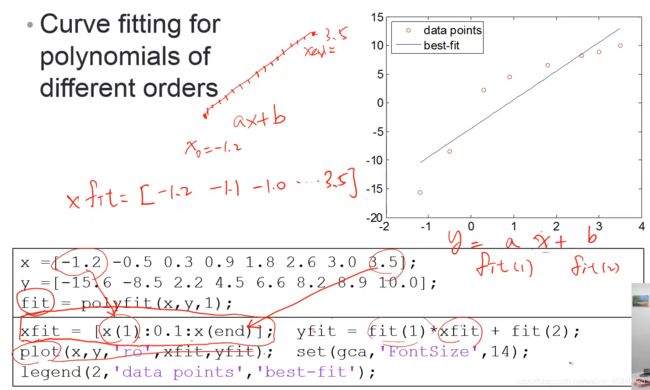
p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数，该阶数是 y 中数据的最佳拟合（在最小二乘方式中）。p 中的系数按降幂排列，p 的长度为 n+1。可以将p(1),p(2)代入拟合方程中计算x对应的拟合y值，如下图一阶多项式拟合；也可以直接使用 polyval(p,x) 来计算，如后图高阶多项式拟合。

[p,S] = polyfit(x,y,n) 还返回一个结构体 S，后者可用作 polyval() 的输入来获取误差估计值。

高阶多项式拟合：

如果你的matlab报错了，将图例换为legend('Data points','Fitted curve','Location','southeast')即可。

相关系数corrcoef()

R = corrcoef(A) 返回 A 的相关系数的矩阵，其中 A 的列表示随机变量，行表示观测值。

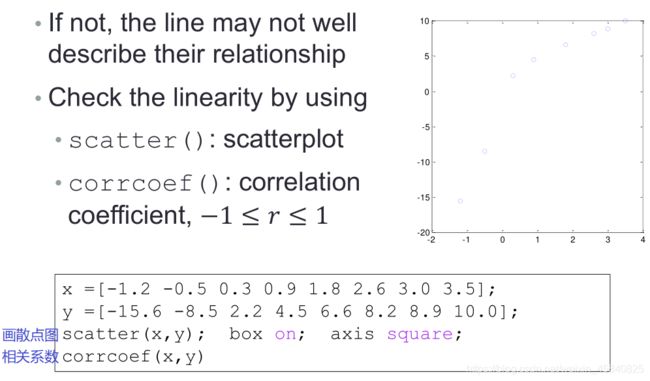
R = corrcoef(A,B) 返回两个随机变量 A 和 B 之间的系数。
[R,P] = corrcoef(___) 返回相关系数的矩阵和 p 值矩阵，用于测试观测到的现象之间没有关系的假设（原假设）。此语法可与上述语法中的任何参数结合使用。如果 P 的非对角线元素小于显著性水平（默认值为 0.05），则 R 中的相应相关性被视为显著。如果 R 包含复数元素，则此语法无效。

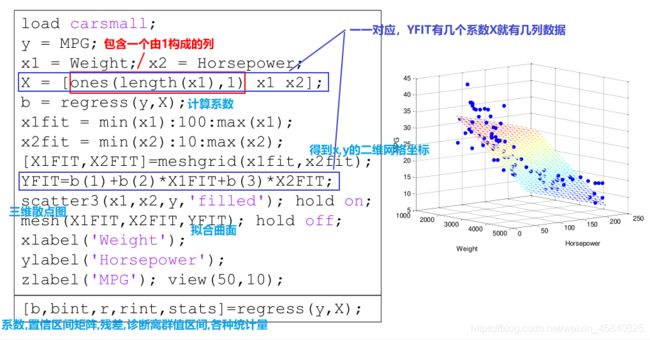
多元线性拟合regress()

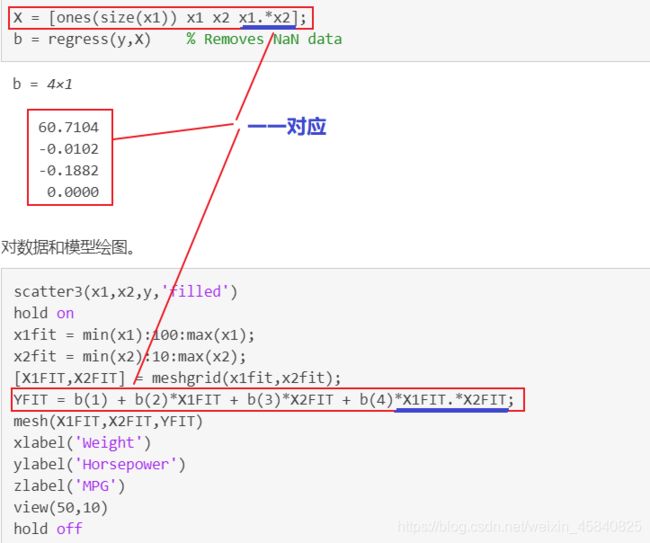
b = regress(y,X) 返回向量 b，其中包含向量 y 中的响应对矩阵 X 中的预测变量的多元线性回归的系数估计值。要计算具有常数项（截距）的模型的系数估计值，请在矩阵 X 中包含一个由 1 构成的列；
[b,bint] = regress(y,X) 还返回系数估计值的 95% 置信区间的矩阵 bint；
[b,bint,r] = regress(y,X) 还返回由残差组成的向量 r。

[b,bint,r,rint] = regress(y,X) 还返回矩阵 rint，其中包含可用于诊断离群值的区间；
[b,bint,r,rint,stats] = regress(y,X) 还返回向量 stats，用以确定线性回归关系的显著性,其中包含 R² 统计量、F 统计量及其 p 值，以及误差方差的估计值。矩阵 X 必须包含一个由 1 组成的列，以便软件正确计算模型统计量。

注意 b=regress(y,X) 中 参数X的每一列数、返回的系数向量b及拟合曲线方程一一对应。上图中的例子表示拟合曲线为 y=b₁+b₂x₁+b₃x₂ ，而下图中的例子则表示拟合曲线为 y=b₁+b₂x₁+b₃x₂+b₄x₂x₃ 。

曲线拟合工具箱cftool

将需要拟合的数据载入到工作区后，使用 cftool 命令调用工具箱，再选择相应数据和拟合选项进行拟合。

工具条：
第一个“main plot”，拟合曲线
第二个“Residuals plot”，残差图
第三个“Contour plot”，轮廓图
第七个“Data cursor”，进行数据提示
第八个“Exclude outliers”，剔除异常值

拟合选项：

• Custom Equations：用户自定义的函数类型；
• Exponential：指数逼近，有2种类型， a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x)；
• Fourier：傅立叶逼近，有8种类型，基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)；
• Gaussian：高斯逼近，有8种类型，基础型是 a1*exp(-((x-b1)/c1)^2)；
• Interpolant：插值逼近，有4种类型，linear、nearest neighbor、cubic spline、shape-preserving；
• Polynomial：多形式逼近，有9种类型；
• Power：幂逼近，有2种类型，a*x^b 、a*x^b + c；
• Rational：有理数逼近，分子、分母各有五种类型；
• Smoothing Spline：平滑样条；
• Sum of Sin Functions：正弦曲线逼近，有8种类型，基础型是 a1*sin(b1*x + c1)
• Weibull：威布尔逼近，只有一种类型a*b*x^(b-1)*exp(-a*x^b)

选用 Custom Equations 来自定义函数逼近时，设置好待拟合函数的系数的StartPoint，Lower和Upper三者的值可以使拟合更加准确。

对同一问题的拟合情况，每次可能都不一样，这取决对于系数的StartPoint的选取.解决方法是在拟合过程中，将系数也作为约束拟合的条件。点击[Fit Options]按钮，调整系数的StartPoint,Lower,Upper三个选项来是拟合更加准确，例如，已知a,b,d都大于0，则将a,b,d的Lower选项设为0，c小于0，则将c的Upper选项设为0。

插值

插值 VS 回归

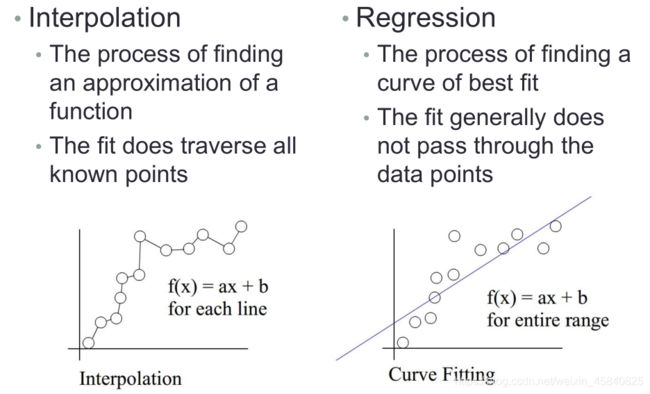
• 插值
  寻找函数近似值的过程；
  拟合会经过所有点
• 回归（拟合）
  寻找最合适的曲线的过程；
  拟合通常不会通过数据点
  
  

线性插值interp1()

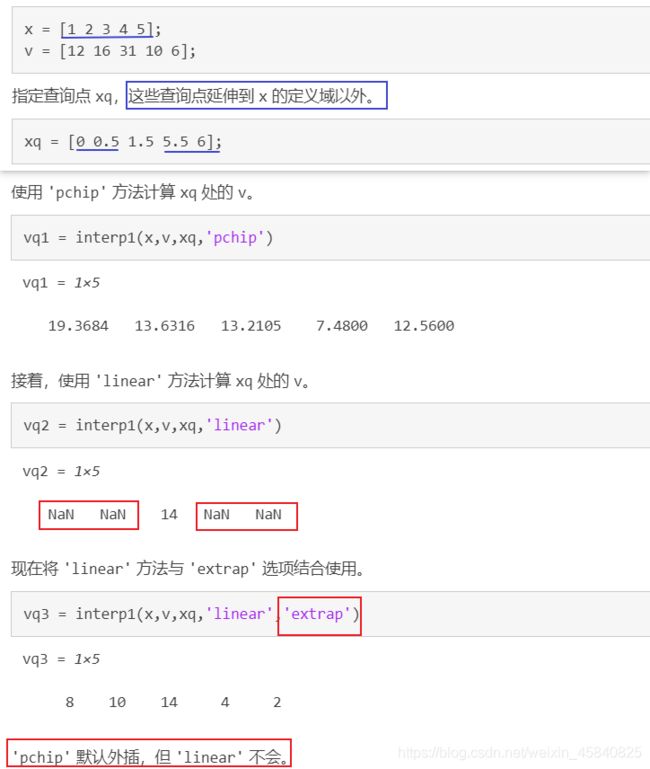
vq = interp1(x,v,xq) 使用线性插值返回一维函数在特定查询点的插入值。向量 x 包含样本点，v 包含对应值 v(x)。向量 xq 包含查询点的坐标。
如果有多个在同一点坐标采样的数据集，则可以将 v 以数组的形式进行传递。数组 v 的每一列都包含一组不同的一维样本值。

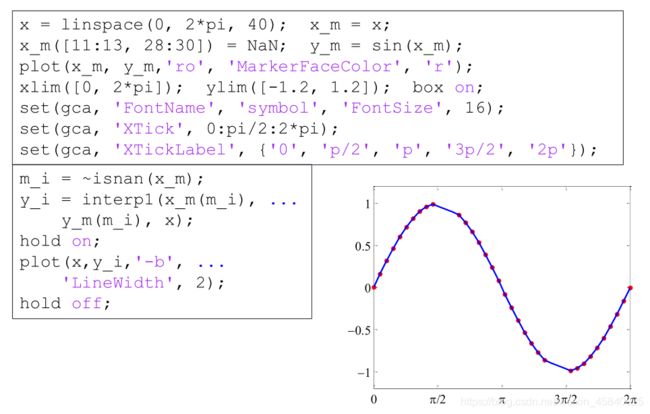
如果 A 的某些元素是 NaN，isnan(A) 返回大小与 A 相同，相应位置包含逻辑值 1 (true) 而其他位置为逻辑值 0 (false) 的数组，~ 则将逻辑值反置。

interp1()的多种插值方法 和 外插

vq = interp1(x,v,xq,method)：method 指定备选插值方法：'linear', 'nearest', 'next', 'previous', 'pchip', 'cubic', 'v5cubic', 'makima' 或 'spline'。默认方法为 'linear'；

vq = interp1(x,v,xq,method,extrapolation)：extrapolation 用于指定外插策略，来计算落在 x 域范围外的点。如果希望使用 method 参数指定的算法进行外插，可将 extrapolation 设置为 ‘extrap’。也可以指定一个标量值，这种情况下，interp1 将为所有落在 x 域范围外的点返回该标量值。

二维网格数据的插值interp2()

Vq = interp2(X,Y,V,Xq,Yq) 使用线性插值返回双变量函数在特定查询点的插入值。结果始终穿过函数的原始采样。X 和 Y 包含样本点的坐标。V 包含各样本点处的对应函数值。Xq 和 Yq 包含查询点的坐标

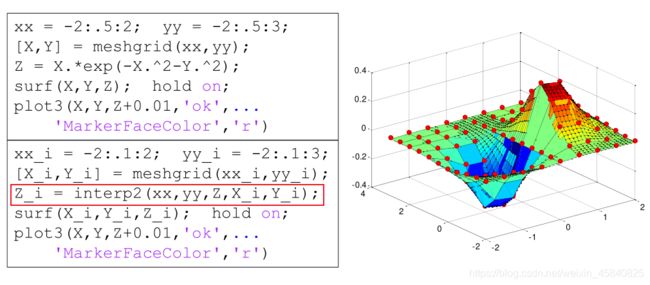
Vq = interp2(___,method)：method 指定备选插值方法：'linear', 'nearest', 'cubic', 'makima' 或 'spline'。默认方法为 'linear'

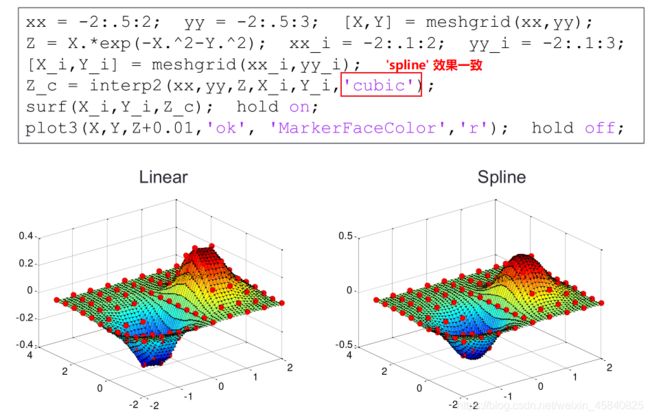
Vq = interp2(___,method,extrapval) 还指定标量值 extrapval，此参数会为处于样本点域范围外的所有查询点赋予该标量值。
如果为样本点域范围外的查询省略 extrapval 参数，则基于 method 参数，interp2 返回下列值之一：对于 ‘spline’ 和 ‘makima’ 方法，返回外插值；对于其他内插方法，返回 NaN 值

三次方样条插值spline()

s = spline(x,y,xq) 返回与 xq 中的查询点对应插值的向量 s。s 的值由 x 和 y 的三次样条插值确定;
pp = spline(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。

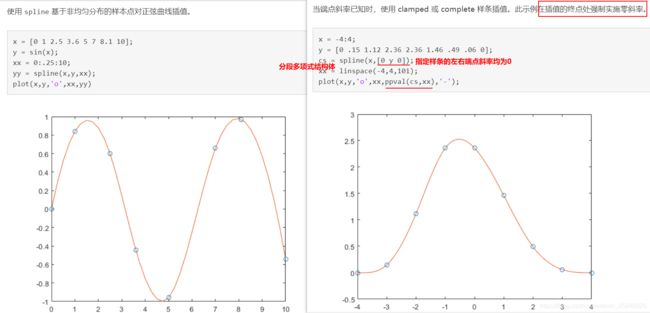
v = ppval(pp,xq) 在 查询点xq 处 计算分段多项式 pp 对应的值；
pp = mkpp(breaks,coefs) 根据其间断数和系数生成分段多项式 pp。使用 ppval 计算特定点处的分段多项式，或使用 unmkpp 提取有关分段多项式的详细信息。

分段三次多项式插值

p = pchip(x,y,xq) 返回与 xq 中的查询点对应的插值 p 的向量。p 的值由 x 和 y 的保形分段三次插值确定；
pp = pchip(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。
相比 spline()，pchip() 可以避免过冲，并且可以准确地连接平台区。这种情况下，它不会在样本点之间自由振动：

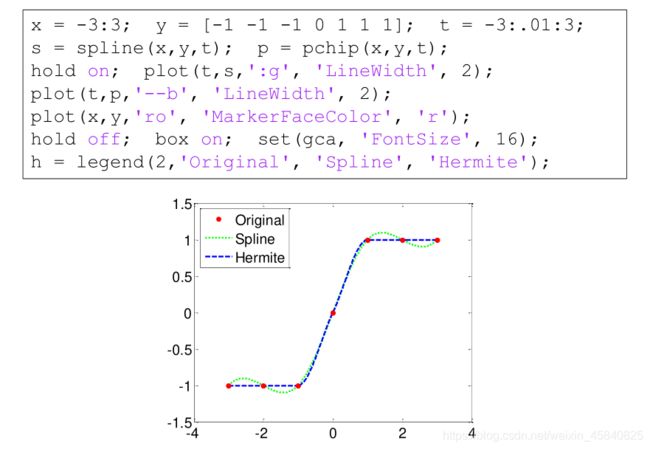
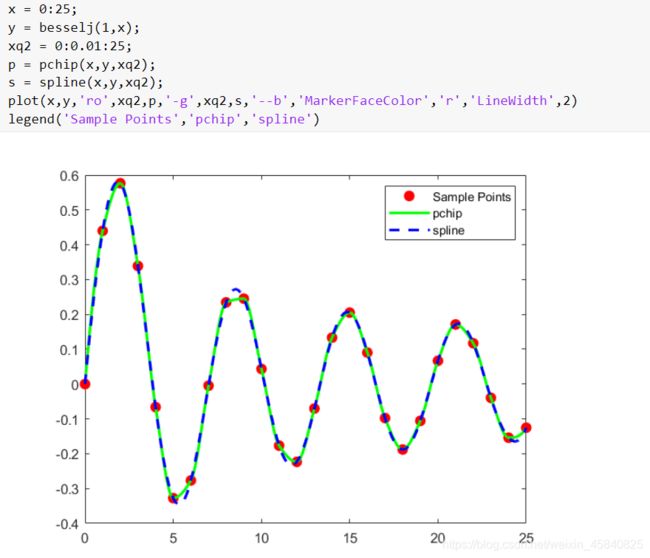
当基础函数振荡时，spline 能够比 pchip 更好地捕获点之间的移动，后者会在局部极值附近急剧扁平化：

练习

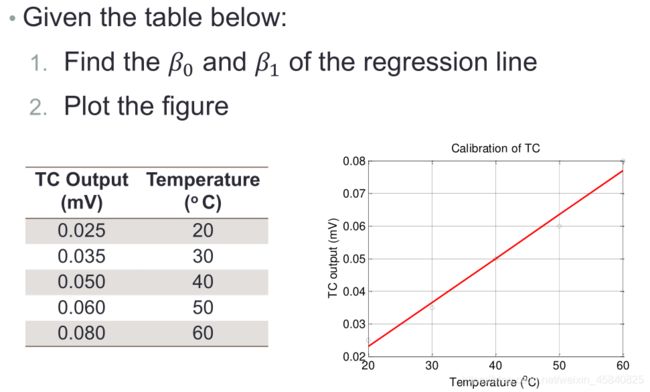
close all;clear all;
y=[0.025 0.035 0.050 0.060 0.080];
x=20:10:60;
fit=polyfit(x,y,1);
xfit=x(1):0.1:x(end);
yfit=polyval(fit,xfit);
plot(x,y,'ro',xfit,yfit,'LineWidth',2);
g=gca;g.FontSize=14;
xlabel('Temperature(℃)');
ylabel('TC output(mV)');
title('Calibration of TC');

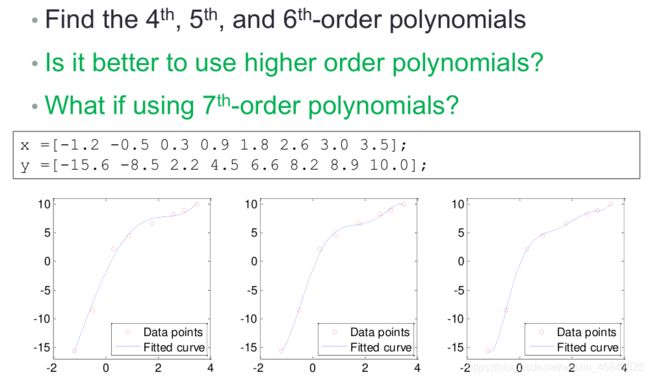
close all; clear all;
x =[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y =[-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
figure('Position', [50 50 1500 400]);
for i=4:6
subplot(1,3,i-3); p = polyfit(x,y,i);
xfit = x(1):0.1:x(end); yfit = polyval(p,xfit);
plot(x,y,'ro',xfit,yfit); set(gca,'FontSize',14);
ylim([-17, 11]); legend('Data points','Fitted curve','Location','southeast');
end

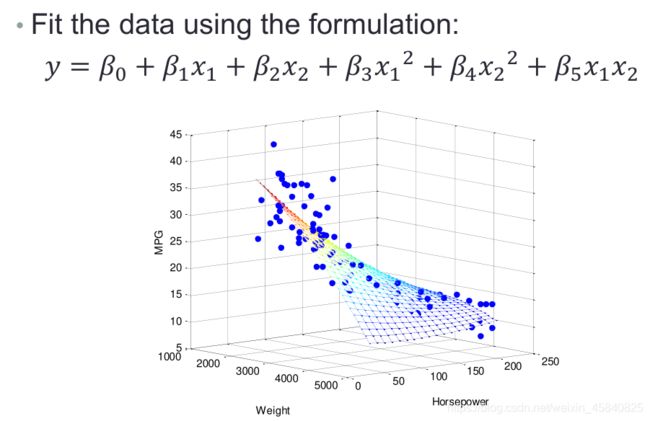
close all; clear all;
load carsmall;
y = MPG;
x1 = Weight; x2 = Horsepower;
X = [ones(length(x1),1) x1 x2 x1.^2 x2.^2 x1.*x2];
b = regress(y,X);
x1fit = min(x1):100:max(x1);
x2fit = min(x2):10:max(x2);
[X1FIT,X2FIT]=meshgrid(x1fit,x2fit);
YFIT=b(1)+b(2)*X1FIT+b(3)*X2FIT+b(4)*X1FIT.^2+b(5)*X2FIT.^2+b(6)*X1FIT.*X2FIT;
scatter3(x1,x2,y,'filled'); hold on;
mesh(X1FIT,X2FIT,YFIT); hold off;
xlabel('Weight');
ylabel('Horsepower');
zlabel('MPG'); view(50,10);

clear all; close all;
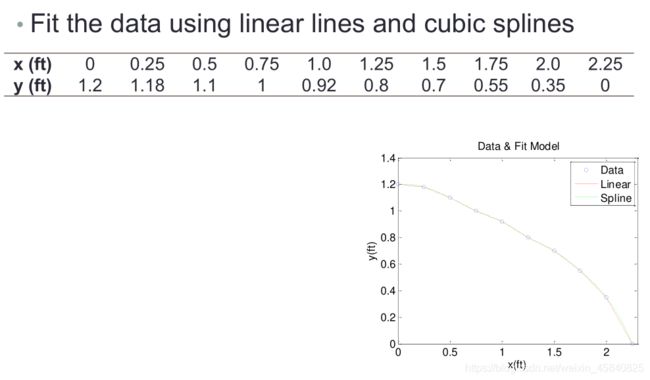
x=[0 0.25 0.5 0.75 1 1.25 1.5 1.75 2.0 2.25];
y=[1.2 1.18 1.1 1 0.92 0.8 0.7 0.55 0.35 0];
X=linspace(0,2.25);
Y1=interp1(x,y,X);
Y2=interp1(x,y,X,'spline');
plot(x,y,'o',X,Y1,'g',X,Y2,'-r','LineWidth',0.8);
legend('Data','Linear','Spline');
xlabel('x(ft)');ylabel('y(ft)');
title('Data & Fit Model');