【数据结构--八大排序】之快速排序
![]()
个人主页 :阿然成长日记 点击可跳转
个人专栏: 数据结构与算法C语言进阶
不能则学,不知则问,耻于问人,决无长进
文章目录
- 一、快速排序的单趟排序
-
- 方法一:霍尔法
-
- 1.基本思路:
- 2.原理图:
- 3.动图:
- 4.代码实现:
- 方法二:挖坑法
-
- 1.基本思路:
- 2.原理图:
- 3.动图:
- 4.代码实现:
- 方法三:前后指针法
-
- 1.基本思路:
- 2.动图
- 3.代码实现:
- 二、快速排序
-
- 1.原理
- 2.递归法:
- 三、快速排序的优化
-
- 1.优化方式:
- 2.优化的使用方法:
- 四、快速排序的完整实现(霍尔法):
- 五、 时间复杂度
前言:
前面,我花费了大量时间学习排序算法,八大排序基本结束,本篇将开始快速排序的讲解。本篇文章适合刚开始学习快速排序的同学,总结的很全面,整理的很清楚,希望能帮到你,加油!
一、快速排序的单趟排序
快速排序的单趟排序:是以一个数作为基准值,实现将数组中比基准数小的数放在基准值的左侧,比基准值大的数放在基准值的右侧。
方法一:霍尔法
霍尔法的由来:霍尔是一个人的名字,他是最初发现快速排序的人,所以,它使用的单趟排序算法被称为霍尔法。
1.基本思路:
用key标记基准值的下标(数组下标0的元素),使用两个指针left和right分别指向待排数组的最左侧和最右侧,right指针找比key基准值小的数,left指针找比key基准值大的数,找到后将两个数交换位置,同时实现大数右移和小数左移,直到left与right相遇则排序完成,最后将key基准值的下标返回,就完成了单趟排序。
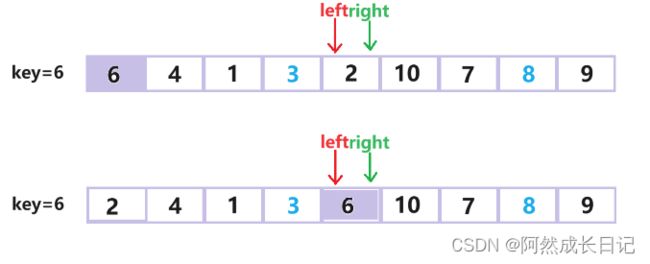
2.原理图:
第二步:right从右边开始先找小于key的值,找到并停下来。

第三步:left从左边开始找大于key的值,找到并停下来。

第四步:交换两个值。Swap(&a[left], &a[right]);
第五步:重复第二步,找小于key的值,找到并停下来。

第六步:第三步:left从左边开始找大于key的值,找到并停下来。
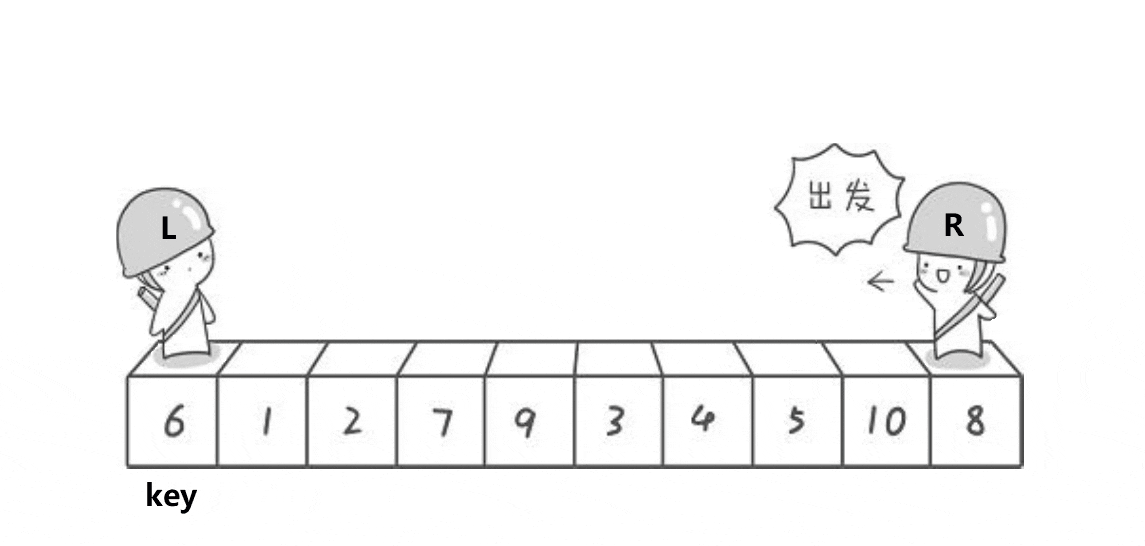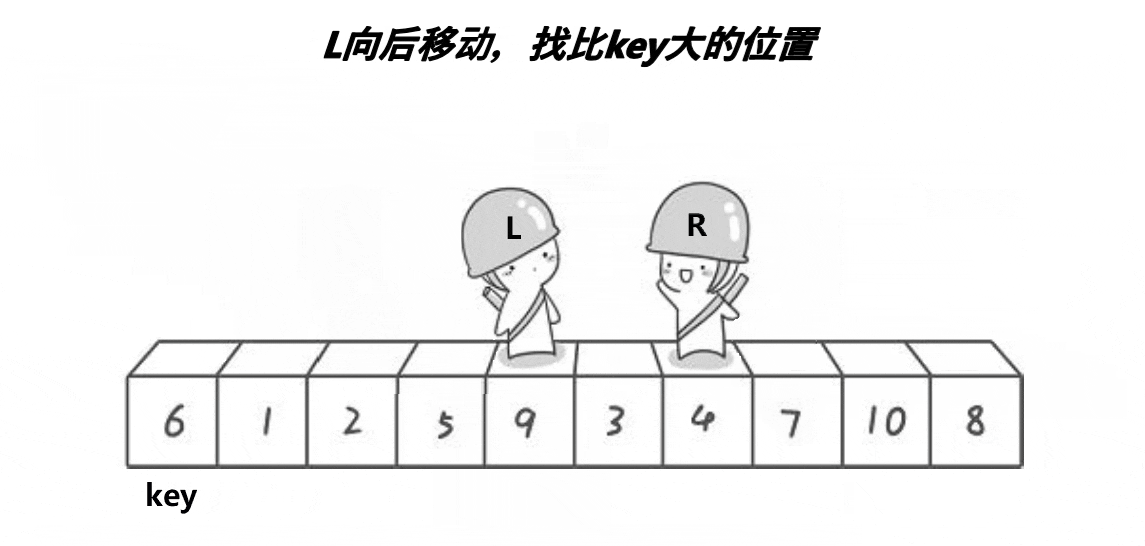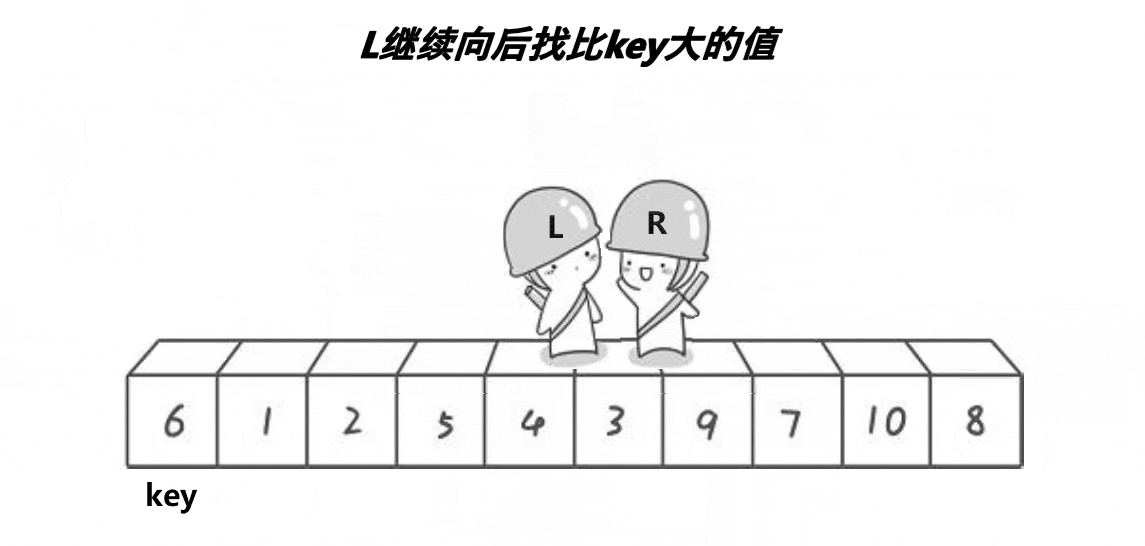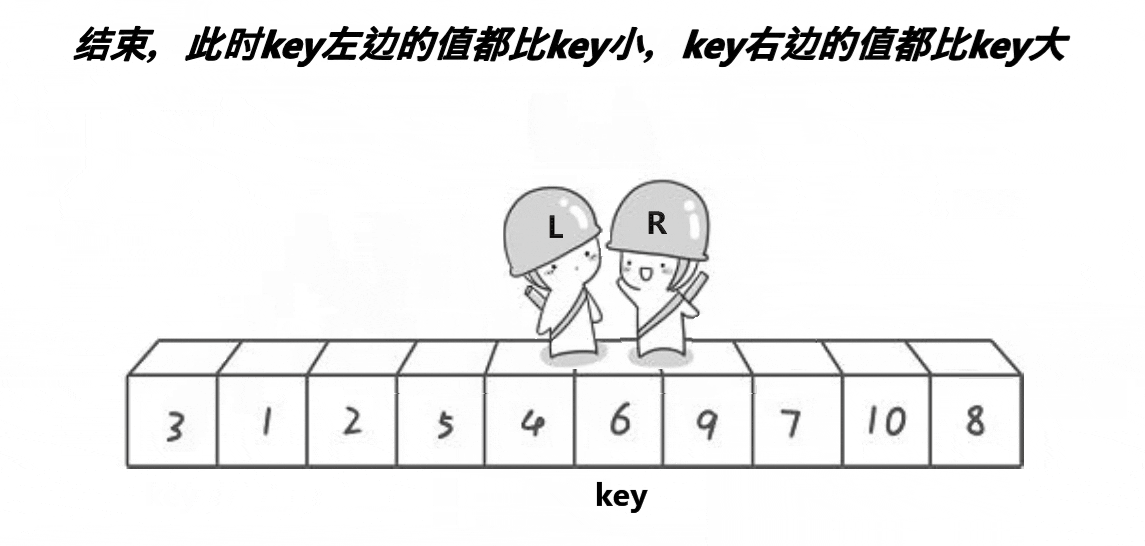
此时left,right相遇,则退出循环,并交换key和left的值。
以上就是一次完整的快速排序的单趟排序。
3.动图:
4.代码实现:
//霍尔法
int Pritition1(int* a, int left, int right)
{
//使用key保存基准值的下标
int key = left;
while (left < right)
{
//先从右边开始向左找小于a[key]的值下标。
while (left < right && a[key] < a[right])
right--;//没找到就一直向左寻找
//再从左边开始向右找大于a[key]的值下标。
while (left<right && a[key]>a[left])
left++;//没找到就一直向右寻找
//交换两个值
Swap(&a[left], &a[right]);
}
//当left和right相遇时,将a[left]赋值给a[key]
//该操作是为了下一轮的排序
Swap(&a[left], &a[key]);
//left相当于分界点坐标
return left;
}
方法二:挖坑法
1.基本思路:
挖坑法是将key基准值用变量单独保存,然后将key的位置空出来形成一个坑,left和right指针分别从左右两端向中心遍历,此时left先指向这个坑,从右边先开始,right找比key小的数,找到后将该数直接放进坑里,并将自己空出来的位置设置为坑,left找比key大的数,找到后将该数放进坑里,并将现在空出来的位置设置为坑,一直遍历,直到left与right相遇,相遇位置一定为坑(left和right必定有一个指向坑),此时将key基准值放进坑内,并返回基准值下标完成单趟排序。
2.原理图:
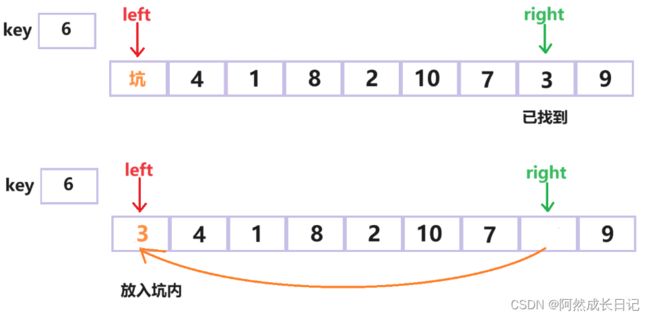
第一步:使用变量key保存基准值。

第二步:right从右边开始先找小于key的值,找到就停下来,将该位置的值放入坑内。
第三步:left从左边开始找大于key的值,找到并停下来,将该位置的值放入坑内。
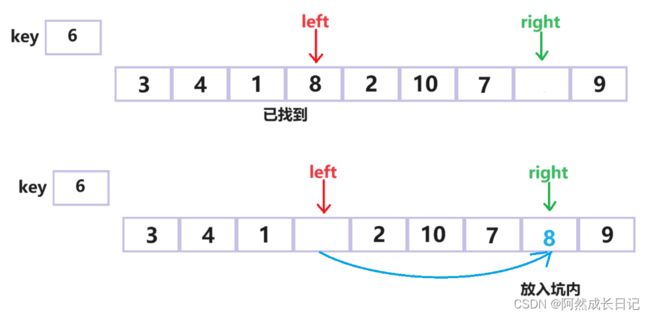
第四步:重复第二步,找小于key的值,找到并停下来。将该位置的值放入坑内。

第五步:left从左边开始找大于key的值,找到并停下来,将该位置的值放入坑内。

注意:此时没有找到就left和right相遇,此时left,right相遇,则退出循环,并交换key放入left。

3.动图:
4.代码实现:
//挖坑法
int Pritition2(int* a, int left,int right)
{
//使用key保存基准值
int key = a[left];
//定义hole是坑;初始坑的位置下标是left
int hole = left;
while (left < right)
{
//从右向左找小于a[key]的值
while (left < right && a[right] >= key)
right--;//没找到就一直向左寻找
a[left] = a[right];//将找到的值放入坑中
hole = right;//并且将找到的位置置为新的坑
while (left < right && a[left] <= key)
left++;//没找到就一直向右寻找
a[right] = a[left];//将找到的值放入坑中
hole = left;//并且将找到的位置置为新的坑
}
a[hole] = key;//将基准值交换到hole位置
//此时hole的位置就是分界点
return hole;
}
方法三:前后指针法
1.基本思路:
(1) 用key保存数组第一个元素作为基准值,定义前指针prev指向第一个数,后指针cur指向前指针的后一个位置。
(2) 由cur挨个遍历数组中的数据,如果cur寻找比key基准值小的数,则prev后移一个位置,并且交换cur和prev所对应的元素值,cur和prev位置不变。
(3) 依次类推直到cur完全遍历完数组,停止。
prev之前的值一定小于key基准值,而prev与cur之间的一定大于基准值
最后将prev处与key位置的元素交换,将基准值下标返回(此时基准值下标已经交换到prev位置)。则完成单趟排序
2.动图
3.代码实现:
//前后指针法
int PartSort3(int* arr, int left, int right)
{
int key = left;
int prev = left;
int cur = left + 1;
while (cur <= right)
{
//arr[cur]小于基准值就交换
//这里做了优化,使用前置++prev
//如果prev+1等于cur则不用交换
if (arr[cur] <= arr[key] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
//交换prev处元素到key位置
Swap(&arr[key], &arr[prev]);
//返回prev,相当于分界点
return prev;
}
二、快速排序
1.原理
快速排序从整体上来看,是以一个选定的数为基准,将数组分为两个子序列,左子序列放比基准数小的,右子序列放比基准数大的数,然后再将子序列以以上方式同样分割,直到数组有序。
快速排序使用递归的方式调用单趟排序,每次调用后都以基准值为界,将数组分为2个子序列,继续排序。一直分到只有一个元素停止。
2.递归法:
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int privot = Pritition1(a, left,right );
QuickSort(a, left, privot - 1);
QuickSort(a, privot + 1, right);
}
三、快速排序的优化
1.优化方式:
采取三数取中法: 在left、right、和中间下标的值中选取一个折中值,基准值不可能为最大值或最小值,可以避免出现最差情况,从而提高快排的时间复杂度。
int GetMidIndex(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[left] < arr[right])
{
if (arr[mid] < arr[left])
{
return left;
}
else if (arr[mid] <arr[right])
{
return mid;
}
else
{
return right;
}
}
else
{
if (arr[mid] < arr[right])
{
return right;
}
else if (arr[mid] < arr[left])
{
return mid;
}
else
{
return left;
}
}
}
2.优化的使用方法:
在我们选择好基准值后,为了保证原来的单趟排序保持原有状态,我们将选好的基准数与数组中第一个数交换位置,然后使用第一个数作为基准值排序
使用方法:
int PartSort(int* arr, int left, int right)
{
//获取基准值,并与left交换位置
int key = GetMidIndex(arr, left, right);
//交换key和left对应的值,但是key指向不变
Swap(&arr[key], &arr[left]);
//将key指向数组开始位置
key = left;
//单趟排序算法
...
}
四、快速排序的完整实现(霍尔法):
//三数取中
int GetMidIndex(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[left] < arr[right])
{
if (arr[mid] < arr[left])
{
return left;
}
else if (arr[mid] < arr[right])
{
return mid;
}
else
{
return right;
}
}
else
{
if (arr[mid] < arr[right])
{
return right;
}
else if (arr[mid] < arr[left])
{
return mid;
}
else
{
return left;
}
}
}
//单趟排序
int Pritition1(int* a, int left, int right)
{
//使用三数取中
int key = GetMidIndex(arr, left, right);
Swap(&arr[key], &arr[left]);
key = left;
while (left < right)
{
//先从右边开始向左找小于a[key]的值下标。
while (left < right && a[key] < a[right])
right--;//没找到就一直向左寻找
//再从左边开始向右找大于a[key]的值下标。
while (left<right && a[key]>a[left])
left++;//没找到就一直向右寻找
//交换两个值
Swap(&a[left], &a[right]);
}
//当left和right相遇时,将a[left]赋值给a[key]
//该操作是为了下一轮的排序
Swap(&a[left], &a[key]);
//left相当于分界点坐标
return left;
}
//采用递归法
void QuickSort(int* a, int left,int right)
{
if (left >= right)
{
return;
}
int privot = Pritition1(a, left,right );
QuickSort(a, left, privot - 1);
QuickSort(a, privot + 1, right);
}
五、 时间复杂度
![]()