A.Almost Correct
待补
B.Anticomplementary Triangle
待补
C.Carrot Trees
题意:给定一个长度为n的数组初始值均为0,给定一个常量k。定义以下两个区间操作
1 l r x 区间[l,r]加x/k
2 l r 区间[l,r]之间大于1的位置-1
求所有操作后 减的操作执行次数。
思路:一眼线段树,但是不知道怎么处理实数和记录等于0的位置。看了题解,借位的思路很妙,
首先如何去处理实数?因为k在所有操作中是一样的 所以我们可以将操作转化为区间加 x ,和区间内大于等于k的值 -k,这样就可以在整数里面操作了。
那么如何去记录所有位置减的次数?记录区间内小于k的数量,如果都是0则不作操作,如果都大于等于k则记录,这些显然会爆时间。题解使用了借位的思想(美丽的数学)
设 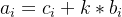 ,ai 为位置i真正的值,ci为解除0的限制的条件下线段树进行各个操作后的值,bi为将ci转变为ai所需要的倍数,也就是重新加上0这个限制条件。
,ai 为位置i真正的值,ci为解除0的限制的条件下线段树进行各个操作后的值,bi为将ci转变为ai所需要的倍数,也就是重新加上0这个限制条件。
考虑这样一个过程,对于操作1 ,我们之间加上x值就可以了,也就是 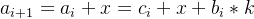
那么对于操作2 则要分情况
情况1
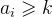 也就是
也就是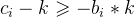 这种情况下我们之间
这种情况下我们之间 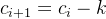 ,
,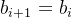
 本身的值已经足够去进行一次 -k 的操作,直接减去就好了,
本身的值已经足够去进行一次 -k 的操作,直接减去就好了,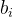 则是继承上一回的值。
则是继承上一回的值。
情况2
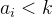 也就是
也就是 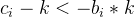
 本身的值不足以支持-k的操作,如果直接减去那么在0的限制下
本身的值不足以支持-k的操作,如果直接减去那么在0的限制下 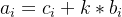 这个等式就不成立了,所以我们要先向bi借一位来保证等式成立。所以
这个等式就不成立了,所以我们要先向bi借一位来保证等式成立。所以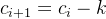 ,
, 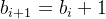
可以看出 b是一个递增的变量,且这两者之间又某种神奇的关系。看了过程可以猜到
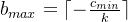
题解的证明十分清晰
所以我们只需要维护每个位置c的历史最小值即可。
//区间修改 单点查询历史最小值
#include
#include
#include
#include
#include
#include
D.Chocolate
题意:有一块n*m的巧克力,每次玩家可以吃(1,1)到(i,j)这个矩形之间的巧克力,每个玩家在各自回合必须吃至少一个单位的巧克力,吃掉最后一块巧克力的人输掉比赛。
(从皇家翻译获得题意后反手喂给队里的博弈选手,就秒了?)
思路:先手直接将巧克力吃成一个L形,可以根据后手的操作去调整自己的操作(对称博弈?)所以只有巧克力为1*1的尺寸的时候先手没有办法去进行对称所以 后手赢
#include
#include
#include
#include
#include
#include
H.Matches
题意:给定两个数组 a b 长度为n 可以在任意数组内进行至多一次交换 定义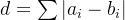
求最小的d
思路:一股浓浓的CF的味道,队友写了分类讨论有道理但是很麻烦。对于每一对  和
和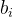 我们可以看做一条线段 d就可以看作所有线段的长度和。然后去最小化d,如果不进行任何操作,d就是初始线段所有的长度。如果线段与线段之间由相交的区域,那么我们就可以减去这个区域*2的长度。
我们可以看做一条线段 d就可以看作所有线段的长度和。然后去最小化d,如果不进行任何操作,d就是初始线段所有的长度。如果线段与线段之间由相交的区域,那么我们就可以减去这个区域*2的长度。
所以我们找到在合法交换下可以消除的最大相交区域。
根据 和
和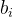 的关系进行分类
的关系进行分类
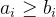 标记为a为右端点 b为左端点
标记为a为右端点 b为左端点
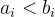 标记为b为右端点 a为左端点
标记为b为右端点 a为左端点
所有线段按照右端点进行由大到小排序,对于每个类维护后缀最小值(最远的左端点)
然后就可以枚举a b,进行快乐的二分了
#include
#include
#include
#include
#include
#include
J.Roulette
题意:有一整数n,每次赌博可以支付  的代价 有
的代价 有 的概率赢获得
的概率赢获得 ,
, 的概率输损失
的概率输损失 。
。
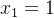
如果第 i-1回合是获胜的那么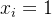 否则
否则 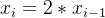
求多赚m元的概率
思路:手玩一下就可以发现每个n到n+1的概率是独立的,内部的概率计算是一个等比数列的和。
#include
#include
#include
#include
#include
#include
K.Subdivision
题意:给定带有n个顶点和m条边的图,可以进行多次一下操作
选择一条边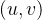 ,由
,由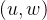 和
和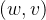 去替换它,w为新加的点
去替换它,w为新加的点
找出与顶点1距离不超过k的最大顶点数
思路:与顶点1的最小距离,可以通过bfs从图重构出各个点与顶点最小的树。那么只要去填满深度小于等于k的位置就可以,每个点可以延申出多少条链去填充通过维护每个点的deg来判断。
注意1和叶子节点的特判.
#include
#include
#include
#include
#include
#include
L.Three Permutations
中国剩余定理 待补
M.Water
题意:有A容量的杯子,B容量的杯子,确定能否通过以下操作确切的喝到x单位的水,如果能输出最小的操作数,否则输出-1
操作1:将两个瓶子中的一个装满水
操作2:将两个瓶子中的一个倒空
操作3:喝掉其中一个瓶子中的所有水
操作4:在不溢出的情况下,尽可能多地将水从一个瓶子转移到另一个瓶子。具体来说,如果两个瓶子分别含有a和b单位的水,他只能从A瓶向B瓶转移min(a,B−b)的水量,或者从B瓶向A瓶转移min(b,A−a)的水量。
题解:exgcd (赛时不会只能看着队友debug, 恼羞成怒,隔天去了解)
题解的证明,,,看不明白。
但是可以从题意里抽象出一个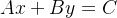 的一个式子,我们的目的之一是求出这个式子。这个很简单,套一个exgcd的板子就可以。接下来就是去将得到的x y 转化成操作数量。
的一个式子,我们的目的之一是求出这个式子。这个很简单,套一个exgcd的板子就可以。接下来就是去将得到的x y 转化成操作数量。
如果x为正数 (我觉得)可以看作 往杯子里到入新的水或者喝掉某个杯子里面的水。
如果x为负数 (我觉得)可以看作 倒空某个杯子里的水或 转移水
y同上
那么当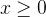 且
且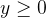 时
时 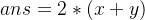 ,倒入新的水与喝水是两部操作故而 *2 下一种情况类似。
,倒入新的水与喝水是两部操作故而 *2 下一种情况类似。
当 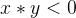 时
时 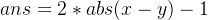 ,因为最后有容器的水我可以不倒掉,所以节约了一次操作 故而 -1。
,因为最后有容器的水我可以不倒掉,所以节约了一次操作 故而 -1。
#include
#include
#include
#include
#include
#include
![]() ,ai 为位置i真正的值,ci为解除0的限制的条件下线段树进行各个操作后的值,bi为将ci转变为ai所需要的倍数,也就是重新加上0这个限制条件。
,ai 为位置i真正的值,ci为解除0的限制的条件下线段树进行各个操作后的值,bi为将ci转变为ai所需要的倍数,也就是重新加上0这个限制条件。![]()
![]() 也就是
也就是![]() 这种情况下我们之间
这种情况下我们之间 ![]() ,
,![]()
![]() 本身的值已经足够去进行一次 -k 的操作,直接减去就好了,
本身的值已经足够去进行一次 -k 的操作,直接减去就好了,![]() 则是继承上一回的值。
则是继承上一回的值。![]() 也就是
也就是 ![]()
![]() 本身的值不足以支持-k的操作,如果直接减去那么在0的限制下
本身的值不足以支持-k的操作,如果直接减去那么在0的限制下 ![]() 这个等式就不成立了,所以我们要先向bi借一位来保证等式成立。所以
这个等式就不成立了,所以我们要先向bi借一位来保证等式成立。所以![]() ,
, ![]()
![]()
![]()
![]() 和
和![]() 我们可以看做一条线段 d就可以看作所有线段的长度和。然后去最小化d,如果不进行任何操作,d就是初始线段所有的长度。如果线段与线段之间由相交的区域,那么我们就可以减去这个区域*2的长度。
我们可以看做一条线段 d就可以看作所有线段的长度和。然后去最小化d,如果不进行任何操作,d就是初始线段所有的长度。如果线段与线段之间由相交的区域,那么我们就可以减去这个区域*2的长度。![]() 和
和![]() 的关系进行分类
的关系进行分类![]() 标记为a为右端点 b为左端点
标记为a为右端点 b为左端点![]() 标记为b为右端点 a为左端点
标记为b为右端点 a为左端点![]() 的代价 有
的代价 有![]() 的概率赢获得
的概率赢获得![]() ,
,![]() 的概率输损失
的概率输损失![]() 。
。![]()
![]() 否则
否则 ![]()
![]() ,由
,由![]() 和
和![]() 去替换它,w为新加的点
去替换它,w为新加的点![]() 的一个式子,我们的目的之一是求出这个式子。这个很简单,套一个exgcd的板子就可以。接下来就是去将得到的x y 转化成操作数量。
的一个式子,我们的目的之一是求出这个式子。这个很简单,套一个exgcd的板子就可以。接下来就是去将得到的x y 转化成操作数量。![]() 且
且![]() 时
时 ![]() ,倒入新的水与喝水是两部操作故而 *2 下一种情况类似。
,倒入新的水与喝水是两部操作故而 *2 下一种情况类似。![]() 时
时 ![]() ,因为最后有容器的水我可以不倒掉,所以节约了一次操作 故而 -1。
,因为最后有容器的水我可以不倒掉,所以节约了一次操作 故而 -1。