6-4 二叉树的非递归遍历 (25分)_学习数据结构--第四章：树与二叉树（二叉排序树）

第四章：树与二叉树(树与二叉树的应用：二叉排序树)

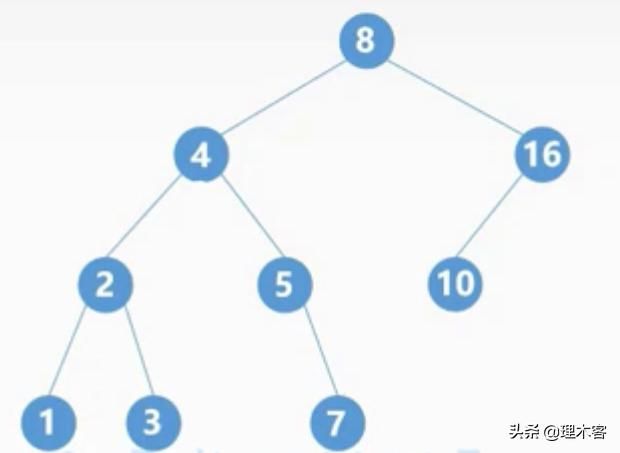
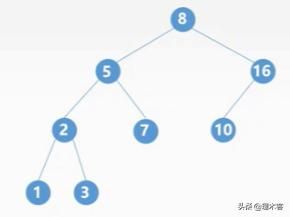
1.二叉排序树

二叉排序树：BST，也称二叉查找树

二叉排序树或者为空树，或为非空树，当为非空树时有如下特点：

· 若左子树非空,则左子树上所有结点关键字值均小于根结点的关键字

· 若右子树非空,则右子树上所有结点关键字值均大于根结点的关键字

· 左、右子树本身也分别是一棵二叉排序树。

注意这里是小于和大于而没有等于，就是说二叉排序树中不存在值相同的结点。

二叉排序树中序遍历：1 2 3 4 5 6 8 10 16

这里可以发现，二叉排序树的中序遍历结果的时递增的，这符合所有的二叉排序树。

二叉排序树的中序遍历序列时一个递增的有序序列

1.1二叉排序树的查找

· 二叉树非空时,查找根结点,若相等则查找成功;

· 若不等,则当小于根结点值时,查找左子树;当大于根结点的值时,查找右子树。

· 当查找到叶节点仍没查找到相应的值,则查找失败。

练习：

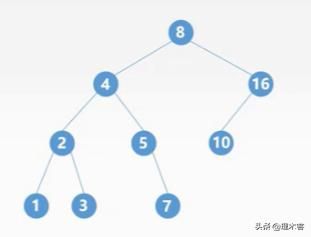
查找5：首先8>5查找左子树，5>4查找右子树，5=5查找成功查找6：首先8>6查找左子树，6>4查找右子树，6>5查找右子树，6<7查找左子树为空，查找失败。

我们根据这个过程其实很容易发现整个查找过程可以使用递归进行完成，可以自行尝试，这里使用非递归查询，代码编写：

参1 二叉树，参2 关键字 参3 保存查找到的结点的双亲结点，是一个指针引用型的变量，这里函数体内对该指针进行修改时，不仅仅会对形参进行修改，而且会对我们传入的变量指针进行修改。

BSTNode *BST_Search(BiTree T,ElemType key,BSTNode *&p){    p = NULL; //双亲结点置为空(根结点没有双亲结点)    while(T != NULL && key != T->data){//树非空且关键字不匹配       p = T; //p指向改结点       if(key < T->data){           T = T->lchild; //循环查找左子树       }else{           T = T->rchild; //循环查找右子树       }    }    return T;}

时间复杂度：O(h) (h为二叉排序树的高度)

1.2二叉排序树的插入

· 若二叉排序树为空,则直接插入结点;

· 若二叉排序树非空,当值小于根结点时,插入左子树;当值大于根结点时,插入右子树;当值等于根结点时不进行插入

练习：

插入6：6<8插入左子树，6>4插入右子树，6>5插入左子树。

代码编写：

//参1 二叉树(注意是引用)，参2 插入值int BST_Insert(BiTree &T,KeyType k){if(T==NULL){ //树为空T = (BiTree)malloc(sizeof(BSTNode));T->key = k;T->lchild = T->rchild = NULL;return 1;}else if(k == T->key){ //相同不插入return 0;}else if(k < T->key){//小于插入左子树中，递归调用return BST_Insert(T->lchild,k);}else{//大于插入右子树中，递归调用return BST_Insert(T->rchild,k);}}

1.3构造二叉排序树

读入一个元素并建立结点,若二叉树为空将其作为根结点;若二叉排序树非空,当值小于根结点时,插入左子树;当值大于根结点时,插入右子树;当值等于根结点时不进行插入。

//参3 插入结点的数量void Create_BST(BiTree &T,KeyType str[],int n){T = NULL;int i=0;while(i

二叉排序树的构造过程就算两个数组的值完全相同，但是构造顺序不同，所生成的二叉排序树就是不同的。

1.4二叉排序树的删除

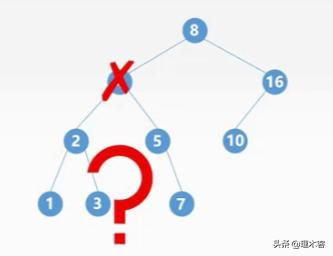
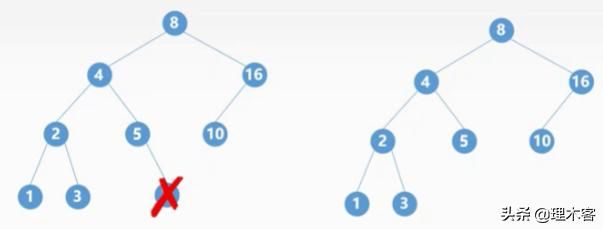
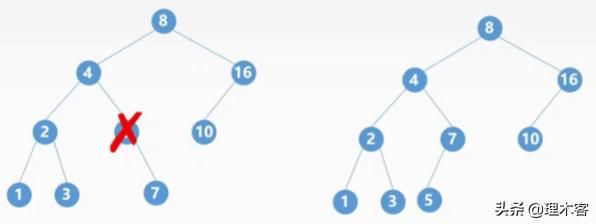
假设我们删除4结点，则剩下的4结点的左子树和右子树该怎么形成结点8的左子树呢？

为了维护二叉树的基本性质，其实删除操作比较复杂的，我们需要分三种情况：

· 1.若被删除的结点z是叶子结点则可以直接删除，不影响

· 2.如果被删除的结点z只有一个子树，则让z的子树成为z父结点的子树，代替z结点。

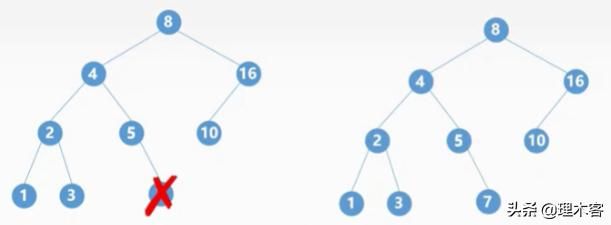
例如我们删除结点5

· 3.若被删除的结点z有两颗子树，则让z的中序序列直接后继代替z，并删去直接后继结点。

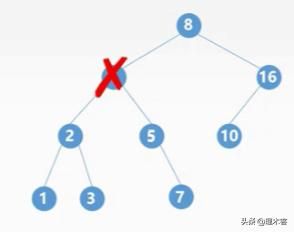
例如我们删除结点4，我们知道结点4的直接后继结点为4的右子树的最左边的那一个结点，这里是5，我们直接将结点4换成结点5，然后直接删除结点5即可，这里为什么能够直接删除？因为这个结点一定是最左侧那个结点，要么没有子树(叶子结点)，要么就是只有右子树(如果有左子树他就不是最左侧的那个结点)，所以删除的时候直接参考上面的两种情况就可以。

思考：在二叉排序树中删除并插入某节点,得到的二叉排序树是否与原来相同？

首先我们删除一个结点7：

接着插入结点7

此时发现删除并插入后二叉排序树相同，这是删除叶子结点的情况，出现了删除并插入后二叉排序树相同，有没有不同的情况？

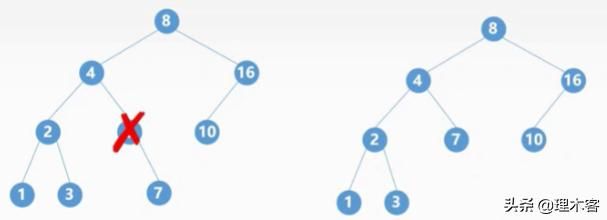
如果我们删除的是一个双亲结点的5

然后插入结点5

此时我们发现删除并插入后二叉排序树不相同了。

故： 在二叉排序树中删除并插入某节点，根据删除并插入的结点类型不同，得到的二叉排序树可能相同，也可能不同。

1.5查找效率

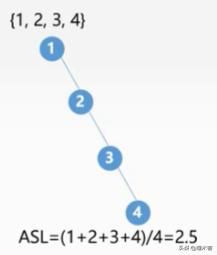
查找长度：查找该节点时所经历的结点的数量。

平均查找长度(ASL)：所有结点查找长度求和取平均值，它取决于树的高度。

例如：

查找效率：O(log2n)

查找效率：O(n)

关于数据结构的知识同名公众号 理木客 同步更新中，下次将会讲解：树与二叉树的应用之平衡二叉树，欢迎大家的关注。

往期文章：

学习数据结构--第一章：绪论

学习数据结构--第二章：线性表(顺序存储、插入、删除)

数据结构第二章：线性表(链式存储、单链表、双链表、循环链表)

学习数据结构--第二章：线性表(顺序表VS链表)

学习数据结构--第三章：栈和队列(栈的基本操作)

数据结构-第三章：栈和队列(队列的基本操作、循环、双端队列)

数据结构-第三章：栈和队列(栈的应用、括号匹配、表达式转换)

学习数据结构--第三章：栈和队列(特殊矩阵的压缩存储)

数据结构第四章：树与二叉树(树的基本概念、基本术语、性质)

数据结构第四章：树与二叉树(二叉树的概念、性质、特殊二叉树)

数据结构第四章：树与二叉树(二叉树的顺序存储和链式存储)

学习数据结构—第四章：树与二叉树(二叉树的遍历和线索二叉树)

学习数据结构 第四章：树与二叉树(树和森林的相关知识)