力扣刷题-动态规划算法6:子序列问题
1. 问题汇总(十三题)

2 子序列(不连续)
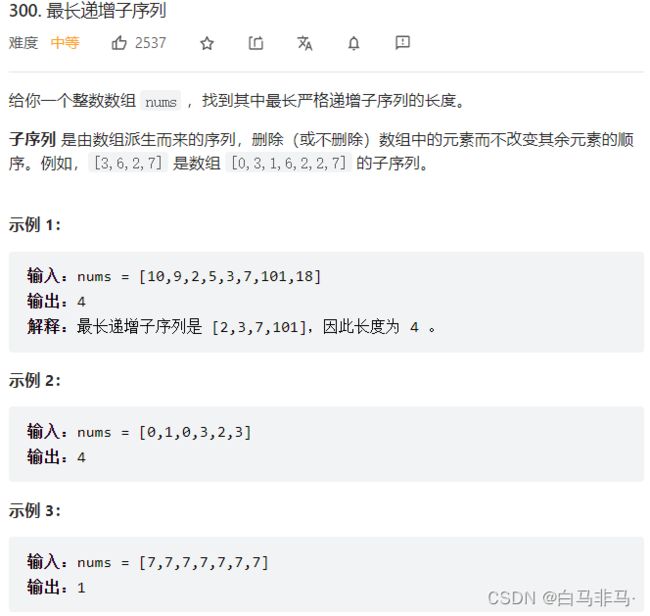
2.1 问题一:300.最长递增子序列(1)
- 问题描述
- 解题思路
1)dp[i] :索引0-i,最大的递增子序列长度
2)思路展示
(1):首先是初始化,每一个位置,长度至少是1
(2):从0-size进行遍历,每遍历一次,都对前面进行比较,如果之前索引位置元素大,则在索引i处长度加一
(3):取dp中的最大值(可以嵌套在之前for循环里面的)
(4):输出最大值 - 代码展示
public int lengthOfLIS(int[] nums) {
//1)dp数组的定义和初始化
int size=nums.length;
int[] dp=new int[size];
Arrays.fill(dp,1); //快速填写默认值
//2)遍历迭代
//dp[i]:取这个值,需要和之前的0-(i-1)的值进行比较,进行加一操作,取最大的。
//dp[i]:如果没有比之前大的,那么就取默认值一
for(int i=0;i<size;i++){
for(int j=0;j<i;j++){
if(nums[i]>nums[j]) dp[i]=Math.max(dp[i],dp[j]+1); //要么保持,要么加一
}
}
//3)取出dp中的最大值
int result=0;
for(int i=0;i<size;i++){
if(dp[i]>result) result=dp[i];
}
//4)输出
return result;
}
2.2 问题二:1143.最长公共子序列(4)
- 题目描述

- 解题思路
1)和题目718. 最长重复子数组非常像,只是一个是连续,一个是不连续,故在它的基础上增加一行代码
2)当c1!=c2的过程中,有dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])。 - 代码书写
public int longestCommonSubsequence(String text1, String text2) {
//这一题与最长相同子序列区别在于,不需要连续,故可以取最大值
//1)dp数组的定义和初始化(初始化也都为零)
//dp[i][j]:截止到字符串一的i位置和字符串二的j位置,最长子序列的值
int size1=text1.length();
int size2=text2.length();
int[][] dp=new int[size1+1][size2+1]; //多拿出一个位置来,方便进行遍历比较
//2)遍历和迭代
for(int i=1;i<=size1;i++){
char c1=text1.charAt(i-1);
for(int j=1;j<=size2;j++){
char c2=text2.charAt(j-1);
if(c1==c2){
dp[i][j]=dp[i-1][j-1]+1;
}else{
//易错点:与最长相同子序列相比,多了一行,保留之前的最大值
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
//3)结果
//System.out.println(Arrays.deepToString(dp));
return dp[size1][size2];
}
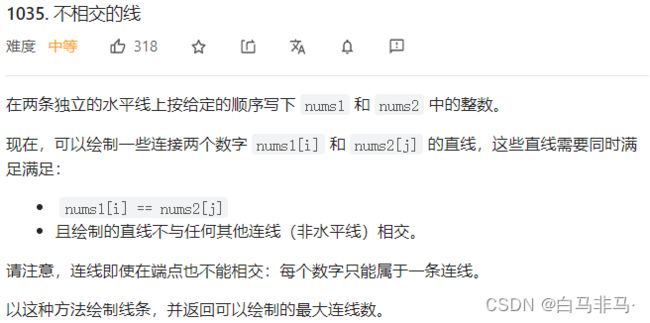
2.3 问题三:1035.不相交的线(5)
- 题目描述

-
解题思路
1)其实这就是一道最长重复子序列的问题,只是换了一种说法,把字符串改为了数字。 -
代码详解
public int maxUncrossedLines(int[] nums1, int[] nums2) {
//其实这道题目就是最长子序列,只是把字符串改为了数组
//1)dp的定义和初始化
int size1=nums1.length;
int size2=nums2.length;
int[][] dp=new int[size1+1][size2+1];
//2)遍历迭代
for(int i=1;i<=size1;i++){
for(int j=1;j<=size2;j++){
//两种情况
if(nums1[i-1]==nums2[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
//3)结果
//System.out.println(Arrays.deepToString(dp));
return dp[size1][size2];
}
3 子序列(连续)
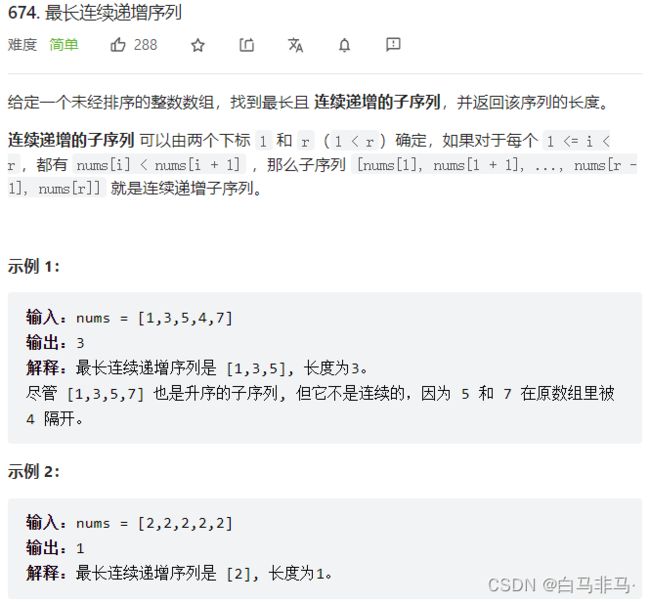
3.1 问题一:674. 最长连续递增序列(2)
- 题目描述
- 思路展示
1)dp[i] :索引0-i,最长连续递增序列长度
2)相比于300.最长递增子序列,这道题目需要的是连续递增,即在上一题基础上简化。
3)不需要遍历i节点之前所有的元素,只需要比较前一个元素
(1):首先是初始化,每一个位置,长度至少是1
(2):遍历位置 i:然后和前面一个的值进行比较,比他大,即为dp[i-1]+1,不然的话,从一开始
(3):找到最大的dp值
(4):输出结果 - 代码解析
public int findLengthOfLCIS(int[] nums) {
//1)定义与初始化
int size=nums.length;
int[] dp=new int[size];
Arrays.fill(dp,1); //自动填充数字初始化
//2)遍历与迭代(只要和前面的比较就好了)
int result=1;
for(int i=1;i<size;i++){
//1)获得dp[i]
if(nums[i]>nums[i-1]) dp[i]=dp[i-1]+1; //否则为1
//1)获得最大的dp[i]
if(dp[i]>result) result=dp[i];
}
//3)输出
return result;
}
3.2 问题二:718. 最长重复子数组(3)
- 题目描述

- 解题思路:
1):暴力方法
(1):进行双层for循环,如果nums1 [i] =nums [j],那么就赋予新的变量,然后直接循环下去
(2):记录最大的相等的个数;当不相等的时候,再返回主循环。
2):动态规划法
(1):dp[i][j]:在nums1索引0-i和nums2索引0-j过程中最大的连续重复子数组大小
(2):赋初值:dp[i] [0]=0;dp[0] [j]=0;默认的。
(3):双循环,都从1开始;
(4):如果nums1 [i] =nums [j],那么dp[i][j]=dp[i-1][j-1]+1;
(5):在双循环遍历的时候记录最大的dp值。

- 代码展示
//暴力方法
public int findLength(int[] nums1, int[] nums2) {
//不用动态规划也能写吧
int Reuslt=0;
int size1=nums1.length;
int size2=nums2.length;
//1)双层for循环
for(int i=0;i<size1;i++){
for(int j=0;j<size2;j++){
//2)循环遍历值,找到最大的连续数组
int i1=i;
int j1=j;
int reuslt=0;
while(i1< size1 && j1<size2 && nums1[i1]==nums2[j1]){
reuslt++;
i1++;
j1++;
}
Reuslt=Math.max(Reuslt,reuslt);
}
}
return Reuslt;
}
//动态规划法
public int findLength(int[] nums1, int[] nums2) {
//动态规划
//1)dp数组的定义与初始化(初始化dp[i][0]=0,dp[0][j]=0)
int size1=nums1.length;
int size2=nums2.length;
int[][] dp=new int[size1+1][size2+1]; //取大一号的值,方便找到i-1
//2)dp数组的遍历和迭代
//d[i][j]:在遍历到数组一的i和数组二的j中,包含的最大子数组长度
//if(nums1[i-1]==numd2[j-1]) dp[i][j]=Math.max(dp[i-1][j-1]+1,1);
int max=0;
for(int i=1;i<=size1;i++){
for(int j=1;j<=size2;j++){
if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
if(dp[i][j]>max) max=dp[i][j];
}
}
//3)结果
//System.out.println(Arrays.deepToString(dp));
return max;
}
//时间复杂度:$O(n × m)$,n 为A长度,m为B长度
//空间复杂度:$O(n × m)$
- 注意事项
1):在动态规划的时候,一定要记录最大的dp[i][j]
2):dp数组的大小为legnth+1。
3.3 问题三:53.最大子序和(6)
- 题目描述

- 解题思路
1)贪心算法
(1):首先一个for循环,遍历数字,然后进行累加
(2):如果和为负数,从最新索引开始,那么就重新计算和,但是保留最大值。
(3):最后的最大值就是答案了。
2)动态规划法
(1):dp[i]:数组从索引0-i之间,最大子序和。
(2):对dp[0]进行赋初值=nums[0];
(3):dp[i]的值等于Math.max(dp[i-1]+nums[i] ,nums[i] )
(4):在遍历的过程中,记录最大的子序和;注意因为连续的关系,最后的最大子序和不一定为最后一个元素。 - 代码详解
//贪心算法
public int maxSubArray(int[] nums) {
//方法一:动态规划思想
//易错点:如果是连续的数,一定需要取最大值,多一个步骤
//1)dp数组的定义和初始化
int[] dp=new int[nums.length];
dp[0]=nums[0]; //这个是能够确定的
//2)遍历迭代
int result=nums[0];
for(int i=1;i<nums.length;i++){
//如果要当前的,那么就要加上之前节点的,如果不要则为现在的
dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
result=Math.max(dp[i],result);
}
//3)输出
//System.out.println(Arrays.toString(dp));
return result;
}
//贪心思想
public int maxSubArray(int[] nums) {
//1)贪心算法(因为有连续,所以一定有遍历选择最大值)
int sum=nums[0];
int result=sum;
for(int i=1;i<nums.length;i++){
sum+=nums[i];
if(sum<nums[i]) sum=nums[i];
result=Math.max(result,sum);
//System.out.print(result+",");
}
return result;
}
4 编辑距离(不连续)
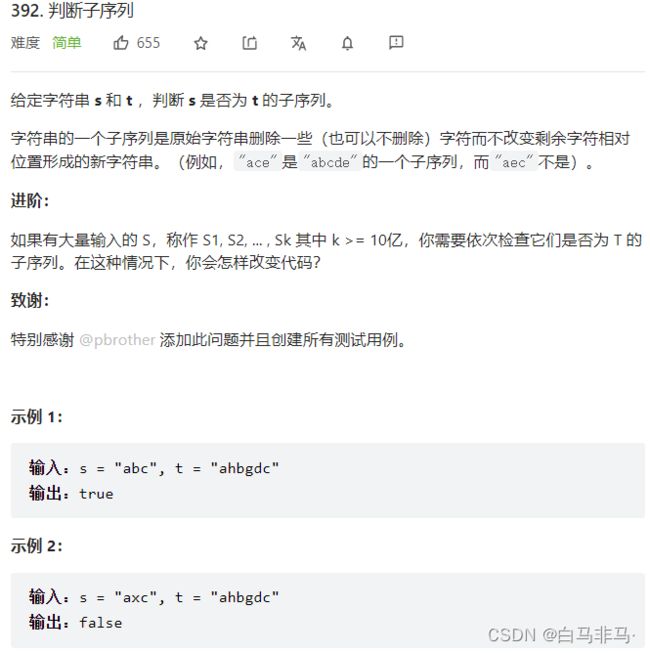
4.1 问题一:392.判断子序列
- 题目描述
- 思路
1)动态规划方法
(1):这题和最长公共子序列很像,只是这道题需要判断最后的子序列一定要是目标串的长度,负责就不是子序列
(2):在进行初始判断的时候,需要考虑一下特殊的情况。
2)双指针算法
(1):进行双层的遍历
(2):如果c1==c2,则循环结束,进入下一个循环,其中目标串的索引是全局变量,只能不断向前的。 - 代码详解
public boolean isSubsequence(String s, String t) {
//方法一:动态规划,看看最长公共子序列的长度是否为最小的子串长度
//和题目最长公共子序列一样的题目,只是这边说明了s是小值。
int size1=s.length();
int size2=t.length();
if(size1==0) return true;
if(size2==0) return false;
int[][] dp=new int[size1+1][size2+1];
//遍历递归(序标从1开始,但是值比较是从0开始的)
for(int i=1;i<=size1;i++){
char c1=s.charAt(i-1);
for(int j=1;j<=size2;j++){
char c2=t.charAt(j-1);
if(c1==c2){
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
//System.out.println(Arrays.deepToString(dp));
if(dp[size1][size2]==size1) return true;
return false;
}
//双指针法
public boolean isSubsequence(String s, String t) {
//双指针法
//特殊情况
if(s.length()==0) return true;
if(t.length()==0) return false;
int j=0; //需要从上一个节点开始,故需要进行全局变量;目标串设为全局变量
for(int i=0;i<s.length();i++){
char c1=s.charAt(i);
boolean flag=false;
for(;j<t.length();j++){
char c2=t.charAt(j);
if(c1==c2) {
flag=true;
j++;
break;
}
}
if(flag==false) return false;
}
return true;
}
4.2 问题二:115.不同的子序列(未做)
4.3 问题三:583. 两个字符串的删除操作(未做)
4.4 问题四:72. 编辑距离(未做)
5 回文(不连续)
5.1 问题一:647. 回文子串
- 题目描述

- 解题思路
1)暴力解法
(1):进行双层遍历,找到起始和总结的索引,然后书写判断回文的函数进行判断
2)动态规划
(0):dp[i][j]:在索引i到索引j的字符是否为回文串
(1):双层遍历,但是是有顺序的
(2):第一层终点 j=0-length; 第二层起点:i=0-i;使用的是索引值
(3):判断方法1:如果在c1=c2的情况下,长度=0,1,2,则dp[i][j]==true;
(4):判断方法2:如果在c1=c2的情况下,长度!=0,1,2,则dp[i][j]==dp[i-1][j-1]
(5):判断方法3:如果在c1!=c2的情况下,dp[i][j]==false,默认选项,无需书写。
(6):统计存在true的个数,其中这一步的工作可以在遍历的时候一起做。 - 代码详解
//暴力解法
public int countSubstrings(String s) {
//通过双层遍历,书写回文串判别式
int reuslt=0;
for(int i=0;i<s.length();i++){
for(int j=0;j<=i;j++){
if(method(s,j,i)==true) reuslt++;
}
}
return reuslt;
}
//回文判别
public static boolean method(String s, int a,int b){
if(b-a==0) return true;
while(a<b){
if(s.charAt(a)==s.charAt(b)){
a++;
b--;
}else{
return false;
}
}
return true;
}
//动态规划写法
public int countSubstrings(String s) {
//1)dp数组的定义和初始化
boolean[][] dp=new boolean[s.length()][s.length()];
//意义:dp[i][j]:从索引为i到索引为j是否为回文串
//2)初始化
for(int i=0;i<s.length();i++) dp[i][i]=true;
//2)遍历迭代
int result=0;
for(int j=0;j<s.length();j++){
for(int i=0;i<=j;i++){
//1)两头相等,进行判断(两种情况)
if(s.charAt(i)==s.charAt(j)){
if(j-i<=2 ){
dp[i][j]=true;
}else{
dp[i][j]=dp[i+1][j-1];
}
}
//2)统计个数
if(dp[i][j]==true) result++;
}
}
//System.out.println(Arrays.deepToString(dp));
return result;
}
5.2 问题二:5.最长回文子串
- 题目描述
- 解题思路
1)在上面一题判断回文串个数的情况下,统计一下是回文串的最大长度值
2)注意点:针对遍历的顺序,一定要好好把握 - 代码详解
public String longestPalindrome(String s) {
//在前面一题判断有多少个回文串的基础上,统计一个长度
//1)dp的定义与初始化
boolean[][] dp=new boolean[s.length()][s.length()];
//2)递归遍历(顺序非常重要,先定好尾巴,然后把尾巴之前的一个个进行判断)
int max=0;
int head=0;
int end=0;
for(int j=0; j<s.length();j++){
for(int i=0;i<=j;i++){
//1)dp数组的赋值
if(s.charAt(i)==s.charAt(j)){ //只考虑相等情况,不等直接默认为false
if(j-i<=2){
dp[i][j]=true;
}else{
dp[i][j]=dp[i+1][j-1];
}
}
//2)dp数组的位置
if(dp[i][j]==true &&j-i>max){
head=i;
end=j;
max=j-i;
}
}
}
return s.substring(head,end+1);
}