堆排序详解

一.前言

堆排序在生活中主要有两大应用场景：一是大数据排序，二是优先队列。其中典型的实例就是解决Topk问题。

二.堆排序思路

现在假设我们已经建好了一个有11个元素的大堆（该堆各个元素的编号从上到下从左到右依次为0,1,2,3……10），那么堆顶元素（编号为0）一定比剩下的10个元素（1到10）都大，首先我们把堆顶元素0号与最后一个元素10号交换，那么我们就将最大的元素放到末尾了，接着我们只需要再将0-9号再调整为大堆，再进行一次首尾交换（注意此时的尾是9号元素），那么9,10号元素分别变为次大和最大的了，依此不断进行直至堆没有元素，就成功得到一个升序序列（即升序建大堆，降序建小堆）。
所以堆排序核心在于堆的创建和调整。

三.堆的创建

这里提前说明一下堆是通过堆的调整创建起来的，所以在创建堆之前我们得先知道堆的调整。

1.堆的向上调整

所谓向上调整，其前提是该元素编号前面的元素都是堆（都是大堆或小堆，这里以小堆为例），现在我们要把该元素及其前面的元素都调整为小堆。

如上图所示，7号之前的元素都是小堆，但这8个元素却不是小堆，这时我们只需要找到该元素的父亲，如果该元素小于其父亲，就进行交换，直至该元素大于等于其父亲节点或该元素已经调整为堆顶。这样就一定可以保证这8个元素都是小堆。

void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;//寻找该元素的父亲，注意堆顶元素编号是0
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

2.堆的向下调整

所谓向下调整，其前提是该元素的左子堆和右子堆都是堆（都是大堆或小堆，这里以大堆为例），但以该元素为堆顶的堆却不是大堆，只需要把该元素向下面进行调整就可以创建创建出一个大堆来。

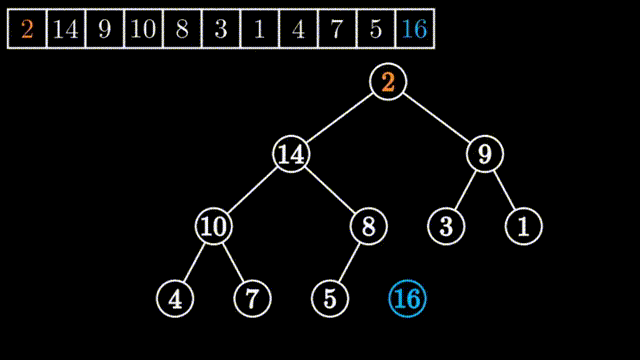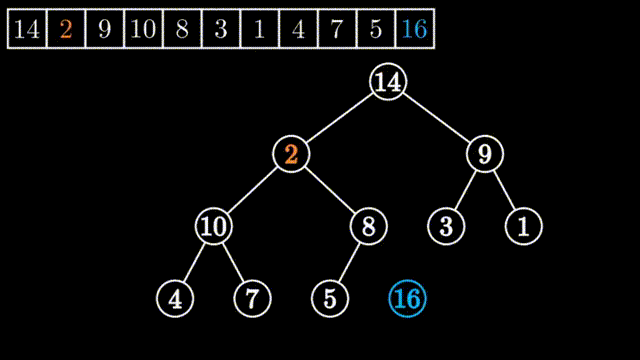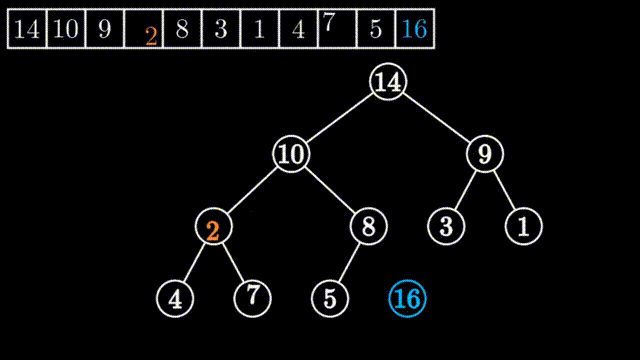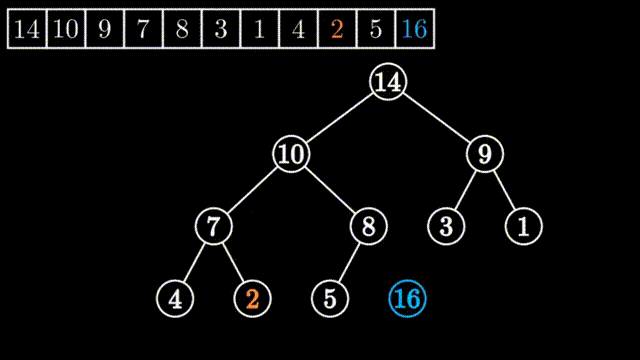
如上图所示，刚开始堆顶的左子堆和右子堆都是大堆，但整个堆不是大堆，要把0到9号元素进行堆的调整为大堆，只需要从其左右两个孩子中挑选出大数的与其进行一次交换，依此不断进行下去，直到要调整的数均大于其左右孩子或要调整的数已经是叶子节点为止。

void HeapAdjustDown(int* a, int size, int parent)
{
	assert(a);

	int leftChild = parent * 2 + 1;
	int rightChild = leftChild + 1;

	while (leftChild < size)
	{
	//找较大的孩子
		int maxChild = leftChild;
		if (rightChild<size && a[leftChild] < a[rightChild])
		{
			maxChild = rightChild;
		}

		if (a[parent] < a[maxChild])
		{
			Swap(&a[parent], &a[maxChild]);//交换两数
		}
		else
		{
			break;
		}
		parent = maxChild;
		leftChild = parent * 2 + 1;
		rightChild = leftChild + 1;
	}
}

3.向上建堆

现在任意给我们一个整型数组，在我们看来这就是一个乱堆，但我们想要将其建成一个大堆，我们可以把第一个元素（编号为0）看成一个堆，该堆只有一个元素，那么1号元素之前的元素都是大堆，现在我们只需要对1号元素进行一次向上调整那么0号和1号元素就构成一个新的大堆了，接着又可以对2号元素进行向上调整，依此进行下去，直到最后一个元素也进行向上调整，至此，一个大堆就建立好了。

void HeapCreate(int* hp, int size)
{
	assert(hp);
	for (int i = 1; i < size; ++i)
	{
		HeapAdjustUp(hp, i);
	}
}

4.向下建堆

现在还是任意给我们一个整型数组，在我们看来他还是一个乱堆，但我们也希望将其建成一个大堆，那么我们可以把每一个叶子节点都看做是大堆，从最后一个非叶子节点开始，向下建堆，直至到根节点，至此，一个大堆就建成了。

如上图：先将4号建成大堆，再将3号建成大堆，依此类推，直至0号。

void HeapCreate(int*hp,int size)
{
	assert(hp);

	for (int i = (size - 1) / 2; i >= 0; i--)
	{
		HeapAdjustDown(hp, size, i);
	}
}

5.两种建堆方式比较

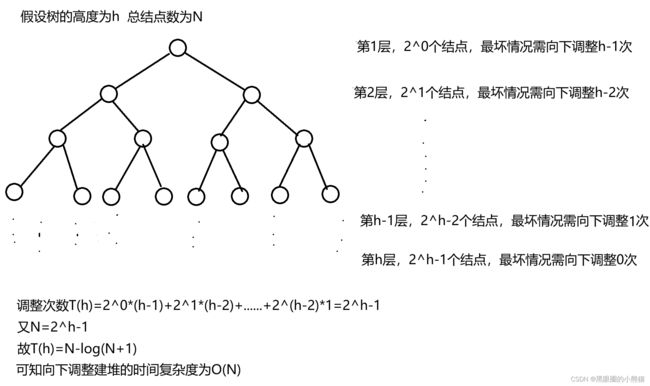
两种建堆方式空间复杂度度均为O(1),下面我们以满二叉树来看时间复杂度：
向上调整：

向下调整：

因此我们优先采用向下调整的方式建堆

四.堆排序

现在我们已经建好了一个11个元素的大堆，接下来要考虑如何排序了。
我们可以将堆的首尾互换，即先把堆顶元素0号与最后一个元素10号交换，那么我们就将最大的元素放到末尾了，接着我们只需要用向下调整的方法再把0-9号元素调整为大堆，再进行一次首尾交换（注意此时的尾是9号元素），同样再把0到8号进行向下调整，那么9,10号元素分别变为次大和最大的了，依此不断进行直至需要进行向下调整的元素个数为0，就成功得到一个升序序列。

void HeapSort(int* hp, int size)
{
	HeapCreate(hp, size);//创建堆
	while (size--)
	{
		Swap(&hp[0], &hp[size]);//首尾交换
		HeapAdjustDown(hp, size, 0);
	}
}

至此，堆排序就算完成了。

下面给出以上完整代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include

//交换两个数
void Swap(int* num1, int* num2)
{
	int temp = *num1;
	*num1 = *num2;
	*num2 = temp;
}

void HeapAdjustUp(int * a, int child)
{
	int parent = (child - 1) / 2;//寻找该元素的父亲，注意堆顶元素编号是0
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapAdjustDown(int* a, int size, int parent)
{
	assert(a);

	int leftChild = parent * 2 + 1;
	int rightChild = leftChild + 1;

	while (leftChild < size)
	{
		int maxChild = leftChild;
		if (rightChild<size && a[leftChild] < a[rightChild])
		{
			maxChild = rightChild;
		}

		if (a[parent] < a[maxChild])
		{
			Swap(&a[parent], &a[maxChild]);
		}
		else
		{
			break;
		}
		parent = maxChild;
		leftChild = parent * 2 + 1;
		rightChild = leftChild + 1;
	}
}

//向下调整建堆
void HeapCreate(int*hp,int size)
{
	assert(hp);

	for (int i = (size - 1) / 2; i >= 0; i--)
	{
		HeapAdjustDown(hp, size, i);
	}
}

//向上调整建堆
//void HeapCreate(int* hp, int size)
//{
//	assert(hp);
//	for (int i = 1; i < size; ++i)
//	{
//		HeapAdjustUp(hp, i);
//	}
//}

void HeapSort(int* hp, int size)
{
	HeapCreate(hp, size);
	while (size--)
	{
		Swap(&hp[0], &hp[size]);
		HeapAdjustDown(hp, size, 0);
	}
}

void Print(int* hp, int size)
{
	int i = 0;
	for (i = 0; i < size; ++i)
	{
		printf("%d ", hp[i]);
	}
}

int main()
{
	int hp[10] = { 9,5,4,1,3,2,8,7,6,10 };
	HeapSort(hp, 10);
	Print(hp, 10);

	return 0;
}

五.复杂度分析

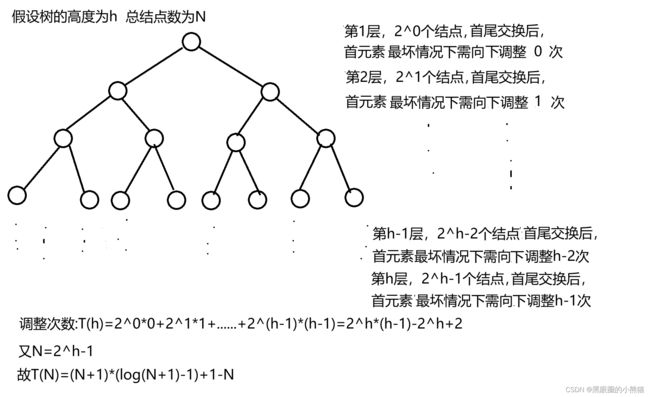
故堆排序
时间复杂度为为O(NlogN)
空间复杂度为O(1)

六.Topk问题

假设现在我有几亿条数据，他们存放在磁盘中，我需要找出他们前K个数据（这K条数据可以放在内存中排序），由于内存大小有限，无法在内存中直接对这几亿条数据进行排序，这个问题就会变得非常棘手，但堆排序却很好的解决了这个问题。
假设我现在想要从存放在磁盘里的三亿个整数中找出最大的前100个数，我可以在内存中先建立一个100个元素的小堆，然后依此从磁盘里面读取数据，如果读取的整数比堆顶元素大，就将堆顶元素替换成读取的数据，再进行一次向下调整，以此类推，直至数据读取完毕，那留在堆里面的元素就是最大的前100个数。

一个数据最坏情况下要进行logK次调整，最坏情况下N个数据都要进行调整，故:
时间复杂度：O(NlogK)
空间复杂度：O(K)

下面是代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include
#include

void CreateData()
{
	// 造数据
	int n = 10000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void Swap(int* num1, int* num2)
{
	int temp = *num1;
	*num1 = *num2;
	*num2 = temp;
}

void HeapAdjustDown(int* a, int size, int parent)
{
	assert(a);

	int leftChild = parent * 2 + 1;
	int rightChild = leftChild + 1;

	while (leftChild < size)
	{
		int minChild = leftChild;
		if (rightChild<size && a[leftChild] > a[rightChild])
		{
			minChild = rightChild;
		}

		if (a[parent] > a[minChild])
		{
			Swap(&a[parent], &a[minChild]);
		}
		else
		{
			break;
		}
		parent = minChild;
		leftChild = parent * 2 + 1;
		rightChild = leftChild + 1;
	}
}

int* HeapCreate(FILE*fout,int k)
{
	assert(fout);

	int* hp = (int*)malloc(sizeof(int) * k);
	if (NULL == hp)
	{
		perror("HeapCreat");
		exit(-1);
	}

	int i = 0;
	for (i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &hp[i]);
	}
	for (i = (k - 1) / 2; i >= 0; i--)
	{
		HeapAdjustDown(hp, k, i);
	}
	
	return hp;
}

void PrintTopK(int k)
{
	FILE* fout = fopen("data.txt", "r");
	if (NULL == fout)
	{
		perror("fopen");
		exit(-1);
	}

	int* hp = HeapCreate(fout, k);
	int x = 0;
	while (EOF!=fscanf(fout, "%d", &x))
	{
		if (x > hp[0])
		{
			hp[0] = x;
			HeapAdjustDown(hp, k, 0);
		}
	}
	while (k--)
	{
		printf("%d ", hp[k]);
	}

	free(hp);
	fclose(fout);
}

int main()
{
	//CreateData();
	PrintTopK(5);

	return 0;
}

七.结语

堆的创建优先选用向下调整建堆，无论是从空间复杂度还是时间复杂度来说，堆排序的性能都是非常不错的。以上就是本文的全部内容了，如果本文有什么不对的地方，恳请指正，当然了，如果你觉得本文对你有所帮助，记得点赞哟！