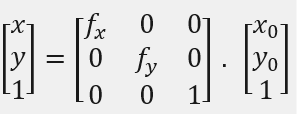opencv图像处理-几何变换

图像的几何变换是图像处理的基础之一，通过几何变换不仅可以产生一些特殊的效果，而且可以简化图像处理过程和分析程序。图像的几何变换最重要的特征是仅改变像素的位置，而不改变图像的像素值。图像的几何变换按性质可以分为图像的位置变换(平移、镜像、旋转)、图像的形状变换(放大、缩小、错切)等基本变换,以及图像的复合变换等。

缩放

原理:

设原图像中的点 $p_0$($x_0$,$y_0$) 按一定比例缩放后，在新图像中的对应点为 P(x,y),则两者之间有如下对应关系

注意: 如果图像在 x 轴和 y 轴方向缩放的比例不相同，则图像会产生几何畸变。

---

代码:

cv.resize(src,dsize,dst,fx,fy,interpolation)

• src: 原图像

• dsize: 目标图像尺寸，必须为整型

• dst: 目标图像

• fx: 水平轴缩放比例

• fy: 竖直轴缩放比例

• interpolation: 插值方法

  • INTER_NEAREST 最邻近插值法
  • INTER_LINEAR 双线性插值法(默认)
  • INTER_AREA 基于局部像素的重采样
  • INTER_CUBIC 基于 4×4 像素邻域的 3 次插值法
  • INTER_LANCZOS4 基于 8×8 像素邻域的 Lanczos 插值

import cv2 as cv
img=cv.imread('lena.jpg')
# 这里将图像放大2倍
res=cv.resize(img, None, fx=2, fy=2)
# 还可以通过另一种方式
# height,width=img.shape[:2]
# res=cv.resize(img,(width*2,height*2),cv.INTER_LINEAR)
cv.imshow('original',img)
cv.imshow('resize',res)
cv.waitKey(0)
cv.destroyAllWindows()

---

处理结果:

---

平移

原理:

设原图像中的点 $p_0$($x_0$,$y_0$) 经过平移变换后，在新图像中的对应点为 P(x,y),则两者之间有如下对应关系

---

代码:

cv.wrapAffine(src,M,dsize,dst,flags,borderMode,borderValue)

• M: 变换矩阵

• flags: 插值方法，同上述缩放变换中的表示

• borderMode: 边界像素模式，默认为BORDER_CONSTANT,边界按常数填充

  • cv.BORDER_CONSTANT: 添加有颜色的常数值边界，通过 borderValue 设置
  • cv.BORDER_REFLECT: 边界元素的镜像
  • cv.BORDER_REFLECT_101 或 cv.BORDER_DEFAULT 同上，只是处理方式稍有不同
  • cv.BORDER_REPLICATE: 重复最后一个元素
  • cv.BORDER_WRAP

• borderValue: 边界填充值，默认为 0，即填充黑色

import cv2 as cv
import numpy as np
img=cv.imread('lena.jpg')
cv.imshow('original',img)
# 图像的高度和宽度
height,width=img.shape[:2]
# 使用numpy数组构造平移矩阵(数据类型为float32),设置x和y方向上平移量均为50
M=np.float32([[1,0,50],[0,1,50]])
res=cv.warpAffine(img,M,(width,height))
cv.imshow('move',res)
cv.waitKey(0)
cv.destroyAllWindows()

---

处理结果:

通过处理结果，我们发现由于没有扩大图像，平移后图像的部分数据会丢失。

---

镜像变换

图像的镜像变换分为水平镜像和垂直镜像。

代码:

cv.flip(src,dst,flip_mod)

• flip_mode: 图像镜像变换的方式
  • flip_mode=0,表示沿 x 轴进行翻转
  • flip_mode>0,表示沿 Y 轴进行翻转
  • flip_mode<0,表示沿 x 和 y 轴进行翻转

import cv2 as cv
img=cv.imread('lena.jpg')
cv.imshow('original',img)
# 沿x轴进行翻转
dstx=cv.flip(img,0)
# 沿y轴进行翻转
dsty=cv.flip(img,1)
# 沿xy轴进行翻转
dstxy=cv.flip(img,-1)
cv.imshow('dstx',dstx)
cv.imshow('dsty',dsty)
cv.imshow('dstxy',dstxy)
cv.waitKey(0)
cv.destroyAllWindows()

---

处理结果:

---

旋转

原理:

设原图像中的点 $p_0$($x_0$,$y_0$)旋转$\theta$角后，在新图像中的对应点为 P(x,y),则两者之间有如下对应关系

---

代码:

cv.getRotationMatrix2D(center,angle,scale)

• center: 原图像的旋转中心
• angle: 图像旋转角度，角度为正则表示逆时针旋转
• scale: 缩放系数

import cv2 as cv
img=cv.imread('lena.jpg')
# 获取图像高度和宽度
height,width=img.shape[:2]
# 设置旋转矩阵,30为旋转度数
M=cv.getRotationMatrix2D((width/2,height/2),30,1)
rotate=cv.warpAffine(img,M,(width,height),cv.INTER_LINEAR)
cv.imshow('rotate',rotate)
cv.waitKey(0)
cv.destroyAllWindows()

---

处理结果:

注意:

1.为避免丢失图像信息，可以通过设置旋转中心、缩放因子、调整窗口大小等方法

2.图像旋转后，因为坐标取值的不同，图像会出现空洞点，因此需要对空洞点进行填充处理，否则边缘将会出现锯齿影响图像质量。处理的方法可以通过插值处理。

---

仿射变换

上面提到的平移和旋转都是仿射变换的特例。

原理:

在仿射变换中，原始图像中的所有平行线在输出图像中仍将平行。
为了找到变换矩阵 M，我们需要输入图像中的三个点及其在输出图像中的对应位置。
然后通过cv.getAffineTransform()找到一个2x3 变换矩阵 M，再将该矩阵将传递给**cv.warpAffine()**进行处理

---

代码:

cv.getAffineTransform(src,dst)

• src: 原图中三个点所组成的矩阵,数据类型为np.float32
• dst: 目标图像中对应的 3 个点所组成的矩阵，数据类型为np.float32

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
img=cv.imread('change.jpg')
# 获取图像的宽、高
height,width=img.shape[:2]
# 原图像三个点和目标图像三个点的位置，数据类型为np.float32
pts1 = np.float32([[50,50],[200,50],[50,200]])
pts2 = np.float32([[10,100],[200,50],[100,250]])
# 通过getAffineTransform()找到2×3的转换矩阵M
M = cv.getAffineTransform(pts1,pts2)
# 将转换矩阵M传递给warpAffine()函数
dst = cv.warpAffine(img,M,(width,height))
# 使用python绘图库绘制图像
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

---

处理结果:

---

透视变换

空间坐标系中的三维物体或对象转变为二维图像的过程称为投影变换，根据投影中心(视点)与投影平面之间距离的不同，投影可以分为平行投影和透视投影。
透视投影即透视变换，透视投影的中心到投影平面之间的距离是有限的，具有透视缩小效应的特点，即三维物体或对象透视投影的大小与形体到投影中心的距离成反比。

原理:

对于透视变换，需要 3x3 变换矩阵。即使在转换后，直线也将保持直线。要找到此变换矩阵，需要在输入图像上有 4 个点，
在输出图像上需要相应的点。在这四个点中，其中三个不应共线。
然后可以通过函数 cv.getPerspectiveTransform() 找到变换矩阵。
再调用 cv.warpPerspective() 应用 3x3 转换矩阵

关键:找到对应的转换矩阵 M

---

代码:

cv.warpPerspective(src,M,dsize,dst,flags,borderMode,borderValue)

• M: 转换矩阵
• flags: 插值方法，同上
• borderMode: 边界像素模式,同上

转换矩阵的获取:

cv.getPerspectiveTransform(src,dst)

• src: 原图像中 4 个点组成的矩阵，数据类型为np.float32
• dst: 目标图像中对应 4 个点组成的矩阵，数据类型为np.float32

import cv2 as cv
from matplotlib import pyplot as plt
import numpy as np
img=cv.imread('change.png')
pts1 = np.float32([[56,65],[368,52],[28,387],[389,390]])
pts2 = np.float32([[0,0],[300,0],[0,300],[300,300]])
M = cv.getPerspectiveTransform(pts1,pts2)
dst = cv.warpPerspective(img,M,(300,300))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()

---

处理结果: