机器学习代码实现篇——SVM

  吴恩达老师课程中的SVM介绍比较简单直观化，但是理论推导不够，这篇博客本着手写代码实现SVM的目标，对SVM进行更深入的讲解。主体推导是根据李航老师《统计学习方法》的相关内容。文末有根据本篇博文思路顺序的SVM实现代码，强烈建议想学习的读者在看完理论推导后自己先手写一遍再看我的代码，一是可以提高自己的编码能力，检验自己对SVM的理解是否到位；二是不同的人编码风格不同，或许能有更好的实现方式。 另外，源码虽开放，但是转载代码的同学请注明出处，谢谢。

1. SVM原理推导

1.1 超平面、函数间隔和几何间隔

  1).超平面
  简单用数学语言描述超平面就是：
$$w\cdot x+b=0\Rightarrow \sum _i^n{w}_i\cdot x_i+b=0$$

  其中，$x=(x_1,x_2,...,x_n{)}^{\prime }$是具有n个特征的数据样本；$w=(w_1,w_2,...,w_n)$是每一项对应的系数。所谓超平面，其实就是因为数据维数超出了直观理解的二维或三维范畴，所以它只是理论上定义的平面，不具有几何意义。
  比如说，当数据只有3维时，超平面就变成$w_1\cdot x_1+w_2\cdot x_2+b=0$，是不是和高中学的一般直线方程$Ax+By+C=0$一样？这时候，超平面其实就是一条能划分二维平面的直线。

  2).函数间隔
  同样以高中几何为例，如何求点$(x_1^{(0)},x_2^{(0)})$到直线$w_1\cdot x_1+w_2\cdot x_2+b=0$的距离呢？有个求解距离的公式：
$$distance=\frac{|w_1\cdot x_1^{(0)}+w_2\cdot x_2^{(0)}+b|}{\sqrt{w_1^2+w_2^2}}$$

  那么，其实$|w_1\cdot x_1^{(0)}+w_2\cdot x_2^{(0)}+b|$就可以一定程度代表点到直线的距离，因为分母其实是个常数。而这个绝对值内数值的正负有什么含义呢？绝对值内的数值为正或负就代表处于超平面的某一侧。对于三维的超平面是如此，对于更高维的超平面也是一样的。
  考虑机器学习中，假设样本是$(x_1^{(i)},x_2^{(i)})$，其对应的分类(这里假设是二分类问题，两个类别分别用+1,-1表示)为$y^{(i)}$，那么其函数间隔就是：
$${\hat{\gamma }}_i=y^{(i)}(w\cdot x^{(i)}+b)$$

  从上述分析可知，函数间隔能一定程度代表样本点到超平面的距离，另外，该距离为正则说明样本在超平面正确的一侧，为负则说明在错误的一侧。

  3).几何间隔
  函数间隔只能一定程度代表样本距离超平面的距离，因为从距离公式可以发现，真实的距离还多除了一个$\sqrt{w_1^2+w_2^2}$，转换为n维的情况其实就是多除一个$||w||=\sqrt{w_1^2+w_2^2+...+w_n^2}$。可以发现，这相当于将超平面的系数标准化为二范数值为1的系数向量。所以几何间隔的数学表达式为：
$${\gamma }_i=y^{(i)}(\frac{w}{||w||}\cdot x^{(i)}+\frac{b}{||w||})=\frac{\hat{\gamma }}{||w||}$$

  这么做有什么意义呢？从函数间隔可以发现，其实所有系数$w,b$同时扩大同样倍数，对于超平面来说是没有区别的，但是尽管超平面和样本不变，此时函数间隔却扩大了同样倍数，这并不是一个理想的情况。而该为几何间隔后，因为对系数进行了标准化，所以无论系数如何扩大缩小，只要超平面和样本不变，其几何间隔就不变。

1.2 间隔最大化原则

  SVM的优化思想是：在所有样本中找到一个超平面对样本空间进行分割(此处假设样本是线性可分的，也就是一定存在超平面能把正样本和负样本完全分开)，使得所有正确分类的样本中，距离超平面最近的样本，其与超平面的距离最大化。因为样本与超平面离的越远，说明这个分类结果越可靠。
  假设每个样本i离超平面的距离为${\gamma }^{(i)}$，用$\gamma$表示离超平面最近的样本与超平面的距离，即
$$\gamma =\underset{i}{\min }{\gamma }^{(i)}\Rightarrow y^{(i)}(\frac{w}{||w||}\cdot x^{(i)}+\frac{b}{||w||})\ge \gamma ,i=1,2,...,m$$

  那么，SVM求取具有最大间隔的超平面的问题，就可以用如下带约束的最优化问题来表示(m表示样本总数)：
$$\underset{w,b}{\max }\gamma ,s.t.y^{(i)}(\frac{w}{||w||}\cdot x^{(i)}+\frac{b}{||w||})\ge \gamma ,i=1,2,...,m$$

  由于上式中，我们可以以任意倍数同时扩大系数$w,b$，所以也就是说，$||w||$是可以任意调整为任何非负值的，因此将约束条件转换为：$y^{(i)}(w\cdot x^{(i)}+b)\ge ||w||\gamma$，将$||w||$调整为$||w||=1/\gamma$，再根据几何间隔和函数间隔的关系，那么原优化问题就可以转换为：
$$\underset{w,b}{\max }\frac{\hat{\gamma }}{||w||},s.t.y^{(i)}(w\cdot x^{(i)}+b)-1\ge 0,i=1,2,...,m$$

  又由于，优化项中$\hat{\gamma }$是函数间隔，其数值的放大与缩小并不影响优化问题的结果(因为$||w||$也会随着$\hat{\gamma }$等比例放大缩小），所以可以忽略不考虑。另外，最大化$1/||w||$相当于最小化$||w||$，为了计算方便，再让其平方后乘以0.5，原优化问题最终转换为：
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2,s.t.y^{(i)}(w\cdot x^{(i)}+b)-1\ge 0,i=1,2,...,m$$

  线性可分样本集的最大间隔的分离超平面是存在且唯一的，具体证明可以参考李航老师的《统计学习方法》。

  上述结果有个硬性前提，就是样本数据是线性可分的，这在大多数情况都是不成立的。因此，上述最优化问题也称为“硬间隔最大化”。
  有硬就有软，如果放宽限定条件，让算法也能处理线性不可分的样本集，则此时的最优化问题就叫做“软间隔最大化”。具体来说，就是把优化问题的约束条件放宽一些，引进一个松弛因子${\xi }_i\ge 0$，使得约束条件变为$y^{(i)}(w\cdot x^{(i)}+b)\ge 1-{\xi }_i$，并将松弛因子作为惩罚项加入原来的目标函数，此时原优化问题就转换为：
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i,s.t.\{\begin{array}{l}{y}^{(i)}(w\cdot x^{(i)}+b)-1+{\xi }_i\ge 0,\\ {\xi }_i\ge 0\end{array},i=1,2,...,m$$

  注意，相比于硬间隔最大化问题，软间隔最大化的最优解中，$w^{\ast }$是唯一的，但是$b^{\ast }$不是唯一的(硬间隔最大化的$b^{\ast }$是唯一的)，而是存在于一个区间内。

1.3 为什么SVM叫支持向量机？

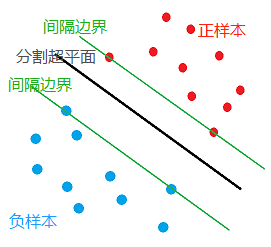
  从最优化问题可以看出，当样本点$x^{(i)}$满足条件$y^{(i)}(w\cdot x^{(i)}+b)-1=0$时，该样本点就是距离超平面最近的样本点，与超平面距离为最小距离的所有空间点可以组成一个间隔边界(如上图绿色边界)，其实其他样本点只要不跨过该边界，那么其他样本点随意移动都对最优分割超平面的求解没有影响，所以相当于是满足上述条件的样本点支持着最优分割超平面。所以满足条件
$$y^{(i)}(w\cdot x^{(i)}+b)-1=0$$

的样本点，也称为“支持向量”(如上图中间隔边界上的几个样本点)。也因此，该算法称为支持向量机。

1.4 带约束的最优化问题求解

  如前所述，SVM算法的核心的解决如下带约束条件的最优问题：
$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i,s.t.\{\begin{array}{l}{y}^{(i)}(w\cdot x^{(i)}+b)-1+{\xi }_i\ge 0,\\ {\xi }_i\ge 0\end{array},i=1,2,...,m$$

  1). 拉格朗日函数构造
  带约束的最优化问题求解，第一反应就是构造拉格朗日函数(关于拉格朗日函数的详细说明，可自行查阅其他资料)。简单来说，要求最优化问题：
$$\min f(x),s.t.\{\begin{array}{l}{c}_i(x)\le 0,i=1,2,...,k\\ ...还可以有更多\le 0的约束条件\\ h_j(x)=0,j=1,2,...,l\\ ...还可以有更多=0的约束条件\end{array}$$

  那么构造的拉格朗日函数就是：
$$L(x,\alpha ,\beta )=f(x)+\sum _{i=1}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)，其中{\alpha }_i\ge 0$$

  考虑最大化拉格朗日函数的问题：$\underset{\alpha ,\beta |\alpha \ge 0}{\max }L(x,\alpha ,\beta )$
  可以发现，如果x不满足约束条件$c_i(x)\le 0$，即存在x使$c_i(x)>0$，那么只要让$\alpha =+\infty$，就可以得到最大化的最优值；同理，如果存在x使$h_j(x)\ne 0$，那么只需要使$\beta h_j(x)=+\infty$，就可以得到最大化的最优值。所以有：
$$\underset{\alpha ,\beta |\alpha \ge 0}{\max }L(x,\alpha ,\beta )=\{\begin{array}{l}f(x),x满足原问题约束条件\\ +\infty ,其他\end{array}$$

  因此，只要对最大化拉格朗日函数的最优问题再取最小化，就可以转换为原始带约束条件的最优化问题：
$$\underset{x}{\min }\underset{\alpha ,\beta |\alpha \ge 0}{\max }L(x,\alpha ,\beta )\Rightarrow 原始带约束条件的最优化问题$$

  花费如此大心思将原始问题转换为拉格朗日函数的最优化问题的原因就在于，拉格朗日函数的最优化问题是不带约束条件的，因为原始问题的约束条件已经包含在拉格朗日函数的公式内部。这样求解起来更方便。

  综上，软间隔最大化问题所构造的拉格朗日函数为(注意约束条件的不等号方向)：
$$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i[y^{(i)}(w\cdot x^{(i)}+b)-1+{\xi }_i]-\sum _{i=1}^m{\mu }_i{\xi }_i$$

  所以软间隔最大化问题就转换为了：$\underset{w,b,\xi }{\min }\underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }L(w,b,\xi ,\alpha ,\mu )$

  2).原始问题的对偶问题
  简单来说，原始问题的对偶问题就是将原来的极小极大值问题转化为极大极小值问题，即：
$$\underset{w,b,\xi }{\min }\underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }L(w,b,\xi ,\alpha ,\mu )互为对偶\iff \underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )$$

  原问题转换为对偶问题求解有几个好处：

• 对偶问题将原始问题中的约束转为了对偶问题中的等式约束
• 原始的$\underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }L(w,b,\xi ,\alpha ,\mu )$问题并不好求，因为它是关于$\alpha ,\mu$系数的函数，这两个系数是构造拉格朗日函数时设定的，其实与原问题并无直接联系。这样求出的最优解${\alpha }^{\ast },{\mu }^{\ast }$应该是和$w,b,\xi$有关系的，后续再求$\underset{w,b,\xi }{\min }$问题就会更加复杂。而转换为先求$\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )$问题后，可以先求出$L(w,b,\xi ,\alpha ,\mu )$对$w,b,\xi$的导数，令其为0，再代入原方程求$\underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }$的问题，则更简单。
• 改变了问题的复杂度。由求特征向量w转化为求比例系数a，在原始问题下，求解的复杂度与样本的维度有关，即w的维度。在对偶问题下，只与样本数量有关；
• 后续引入核函数更加方便；

  当然，通常情况下原始问题的最优解和对偶问题的最优解只是有一定不等式关系，并不是相等的。要让原始问题的最优解和对偶问题相同，则必须满足以下定理：
  函数$f(x)$和$c_i(x)$是凸函数，$h_j(x)$是仿射函数(当前情况下不存在$h_j(x)$），并且不等式约束$c_i(x)$是严格可行的，则$x^{\ast }$、${\alpha }^{\ast }$和${\beta }^{\ast }$同时是原始问题和对偶问题的最优解的充要条件是，必须满足以下KKT条件：
$$\{\begin{array}{l}{▽}_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0\\ {\alpha }_i^{\ast }{c}_i(x^{\ast })=0,i=1,2,...,k\\ c_i(x^{\ast })\le 0,i=1,2,...,k\\ {\alpha }_i^{\ast }\ge 0,i=1,2,...k\\ h_j(x^{\ast })=0,j=1,2,...,l\end{array}$$

转换为当前目标问题即为：
$$\{\begin{array}{l}{▽}_{w,b,\xi }L(w^{\ast },b^{\ast },{\xi }^{\ast },{\alpha }^{\ast },{\mu }^{\ast })=0\\ {\alpha }_i^{\ast }[y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1+{\xi }_i^{\ast }]=0,i=1,2,...,k\\ y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1+{\xi }_i^{\ast }\ge 0,i=1,2,...,k\\ {\alpha }_i^{\ast }\ge 0,i=1,2,...k\end{array}\iff \{\begin{array}{l}{w}^{\ast }={\sum }_{i=1}^m{\alpha }_i^{\ast }{y}^{(i)}{x}^{(i)}\\ {\sum }_{i=1}^m{\alpha }_i^{\ast }{y}^{(i)}=0\\ C-{\alpha }_i^{\ast }-{\mu }_i^{\ast }=0\\ {\alpha }_i^{\ast }[y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1+{\xi }_i^{\ast }]=0,i=1,2,...,k\\ {\mu }_i^{\ast }{\xi }_i^{\ast }=0\\ y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1+{\xi }_i^{\ast }\ge 0,i=1,2,...,k\\ {\alpha }_i^{\ast }\ge 0{\xi }_i^{\ast }\ge 0{\mu }_i^{\ast }\ge 0,i=1,2,...k\end{array}$$

  3).对偶问题的求解
  先求解问题：$\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )$
$${▽}_{w}L(w,b,\xi ,\alpha ,\mu )=w-\sum _{i=1}^m{\alpha }_i{y}^{(i)}{x}^{(i)}=0$$

$${▽}_{b}L(w,b,\xi ,\alpha ,\mu )=-\sum _{i=1}^m{\alpha }_i{y}^{(i)}=0$$

$${▽}_{{\xi }_i}L(w,b,\xi ,\alpha ,\mu )=C-{\alpha }_i-{\mu }_i=0$$

  注意，上式中的$w$和$x^{(i)}$都是多维向量，而不是标量。
  将求导后的三个等式代入拉格朗日方程中，即可得到：
$$\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )=-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}\cdot x^{(j)})+\sum _{i=1}^m{\alpha }_i$$
  $\because {\mu }_i=C-{\alpha }_i$，所以$\underset{\alpha ,\mu |\alpha ,\mu \ge 0}{\max }\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )$可以转换为：
$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}\cdot x^{(j)})+\sum _{i=1}^m{\alpha }_i,s.t.\{\begin{array}{l}{\sum }_{i=1}^m{\alpha }_i{y}^{(i)}=0\\ 0\le {\alpha }_i\le C\end{array}$$

  取负号，将上述问题转换为最小化问题：
$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}(x^{(i)}\cdot x^{(j)})-\sum _{i=1}^m{\alpha }_i,s.t.\{\begin{array}{l}{\sum }_{i=1}^m{\alpha }_i{y}^{(i)}=0\\ 0\le {\alpha }_i\le C\end{array}$$

  只要求得上述最优化问题的解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_m^{\ast })$，那么就可以根据下式求：
$$w^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}^{(i)}{x}^{(i)}$$

  由于要满足KKT条件，所以有：
$$\{\begin{array}{l}{\mu }_i^{\ast }=C-{\alpha }_i^{\ast }\\ {\mu }_i^{\ast }{\xi }_i^{\ast }=0\\ {\alpha }_i^{\ast }[y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1+{\xi }_i^{\ast }]=0,i=1,2,...,k\end{array}$$

  当$0<{\alpha }_i^{\ast }<C$时，${\mu }_i^{\ast }\ne 0\Rightarrow {\xi }_i^{\ast }=0\Rightarrow y^{(i)}(w^{\ast }\cdot x^{(i)}+b^{\ast })-1=0$，所以有：
$$b^{\ast }=y^{(j)}-\sum _{i=1}^m{y}^{(i)}{\alpha }_i^{\ast }(x^{(i)}\cdot x^{(j)})$$

1.5 核函数(kernel)

  上述情况中，都涉及到样本互相之间的内积$(x^{(i)}\cdot x^{(j)})$。这都是线性支持向量机，最终计算出来的超平面都是线性的。
  假设存在非线性映射函数$\varphi (x^{(i)})$将样本$x^{(i)}$从输入空间映射到新的特征空间，再将上述过程中的$(x^{(i)}\cdot x^{(j)})$替换为$K(x^{(i)},x^{(j)})=(\varphi (x^{(i)})\cdot \varphi (x^{(j)}))$。那么，上述过程就相当于先将样本映射到非线性特征空间，再对新的特征空间进行线性SVM求解。这样，就相当于求解非线性问题了，引入核函数的SVM就称为非线性支持向量机。下面的SMO算法介绍就是采用引入核函数后的SVM推导结果。
  这个过程相当于线性回归$y=wx+b$中，先将特征进行非线性映射$\varphi (x)$（比如$\varphi (x)=x^2$），然后再求其线性回归的解$y=w\varphi (x)+b$是一个道理。因为核函数的概念其实是可以扩展到其他所有机器学习算法中的，只是其在SVM中显得尤为重要。
  核函数的具体数学含义以及什么函数可以作为核函数，都不属于本篇内容的讨论范畴，感兴趣的读者可以自行查阅相关书籍加深对核函数的理解。以下列出常见的两种核函数：
  1).多项式核函数
$$K(x,z)=(x\cdot z+1{)}^p,其中p是超参数，是多项式次数$$

  2).高斯核函数
$$K(x,z)=exp(-\frac{||x-z|{|}^2}{2{\sigma }^2})$$

  那么，现在最关键的问题只剩下一个，即如何求最优化问题的解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_m^{\ast })$，求解方法就是使用启发式算法——序列最小最优化算法(SMO,sequential minimal optimization)

1.6 SMO算法

  该算法用来求解最优化问题：$\underset{\alpha }{\min }\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}^{(i)}{y}^{(j)}K(x^{(i)}\cdot x^{(j)})-{\sum }_{i=1}^m{\alpha }_i,s.t.\{\begin{array}{l}{\sum }_{i=1}^m{\alpha }_i{y}^{(i)}=0\\ 0\le {\alpha }_i\le C\end{array}$
  算法核心思想是：

• 如果所有变量$\alpha$都能使优化问题所有样本都满足KKT条件，那么这时的$\alpha$就是最优解。
• 否则，从中选择两个变量${\alpha }_i,{\alpha }_j$，其他$\alpha$固定不变，将问题转换为一个二次规划的子问题。
• 求解只关于${\alpha }_i,{\alpha }_j$的双变量最优化问题的解，更新${\alpha }_i,{\alpha }_j$，然后再回到步骤1判断此时的变量$\alpha$是否让所有样本满足KKT条件，如果不满足，则继续进行步骤2。直到满足KKT条件为止。

  根据算法的核心思想，可以知道SMO最关键的问题有两个：
  1).不失一般性，假设选择了变量${\alpha }_1,{\alpha }_2$，如何求解双变量的最优化问题，得到子问题的最优解？
  在固定其他变量后，原问题转换为：
$$\underset{{\alpha }_1,{\alpha }_2}{\min }\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y^{(1)}{y}^{(2)}{K}_{12}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y^{(1)}{\alpha }_1\sum _{i=3}^m{y}^{(i)}{\alpha }_i{K}_{i1}+y^{(2)}{\alpha }_2\sum _{i=3}^m{y}^{(i)}{\alpha }_i{K}_{i2}$$

$$s.t.\{\begin{array}{l}{\alpha }_1{y}^{(1)}+{\alpha }_2{y}^{(2)}=-{\sum }_{i=3}^m{\alpha }_i{y}^{(i)}=常数A\\ 0\le {\alpha }_i\le C,i=1,2\end{array}$$

  其中$K_{ij}=K(x^{(i)},x^{(j)})$是核函数的缩写。式中省略了不含${\alpha }_1,{\alpha }_2$的常数项。
  令优化函数对${\alpha }_2$求导可得(具体推导过程可以参见《统计学习方法》，在此不赘述了)：
$${\alpha }_2^{new,unc}={\alpha }_2^{old}+\frac{y^{(2)}(E_1-E_2)}{\eta }$$

  其中$E_i=g(x^{(i)})-y^{(i)}={\sum }_{j=1}^m{y}^{(i)}{\alpha }_i{K}_{ji}-y^{(i)},i=1,2$，表示对输入$x^{(i)}$的预测值与真实值的差值。
  再根据约束条件对最优解进行裁剪后，可得最终的结果：
$${\alpha }_2^{new}=\{\begin{array}{l}H,{\alpha }_2^{new,unc}>H\\ {\alpha }_2^{new,unc},L\le {\alpha }_2^{new,unc}\le H\\ L,{\alpha }_2^{new,unc}<L\end{array}$$

$$其中,若y^{(1)}\ne y^{(2)}\{\begin{array}{l}L=\max (0,{\alpha }_2^{old}-{\alpha }_1^{old})\\ H=min(C,C+{\alpha }_2^{old}-{\alpha }_1^{old})\end{array},若y^{(1)}=y^{(2)}\{\begin{array}{l}L=\max (0,{\alpha }_2^{old}+{\alpha }_1^{old}-C)\\ H=min(C,{\alpha }_2^{old}+{\alpha }_1^{old})\end{array}$$

  求得${\alpha }_2^{new}$后，再根据约束条件即可得到：
$${\alpha }_1^{new}=(常数A-{\alpha }_2^{new}{y}^{(2)})/y^{(1)}$$

  2).如何从$\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_n)$中选择两个变量作为子问题的研究对象？
  第一个变量的选择：
  选择不满足KKT条件中，程度最严重的样本点(假设该样本点下标为i)，其下标对应的${\alpha }_i$。
  此处选用的KKT条件是：
$$\{\begin{array}{l}{\alpha }_i=0\iff y^{(i)}g(x^{(i)})\ge 1\\ 0<{\alpha }_i<C\iff y^{(i)}g(x^{(i)})=1\\ {\alpha }_i=C\iff y^{(i)}g(x^{(i)})\le 1\end{array}$$

  那么，最不符合的样本点就是先计算$Z(i)=y^{(i)}g(x^{(i)})-1$，然后根据以下情况求取最大值：
$$最不满足KKT的样本下标=\underset{i}{\arg }\max \{\begin{array}{l}\max (-Z(i))，{\alpha }_i=0\\ \max (|Z(i)|)，0<{\alpha }_i<C\\ \max (Z(i))，{\alpha }_i=C\end{array}$$

  第二个变量的选择：
  因为${\alpha }_1$已经确定了，所以$E_1$也确定了。那么选择第二个参数的方式如下(推导略)：
$$第二个变量的下标=\{\begin{array}{l}{\arg }_i\min E_i,i\ne 1,且E_1>0\\ {\arg }_i\max E_i,i\ne 1,且E_1<0\end{array}$$

  所以在代码实现的时候，通常需要提前计算好每一轮的$g(x^{(i)}),E_i$以及核函数的数值$K_{ij}$。

2. SVM代码详解

2.1 源码分析

class SVM(object):
    """二分类SVM"""
    def __init__(self,features,labels,kernel='linear',C=1,eps=10e-4,maxIter=1000):
        self.m, self.n = features.shape  # 样本数量m和样本特征数量n
        self.features = features
        self.labels = labels
        self.kernel = kernel
        self.C = C  # 正则项的系数，超参数
        self.eps = eps  # 迭代结束的允许精度
        self.alpha = np.zeros((self.m,1))
        self.b = 0
        self.maxIter = maxIter  # 最大迭代次数限制
        self.g = np.zeros((self.m,1))  # 记录g(x_i)
        self.k = np.zeros((self.m,self.m))  # 记录K(x_i,x_j)，是对称阵
        self.E = np.zeros((self.m, 1))  # 记录E[i] = g[i] - labels[i]

    def __check_KKT(self,i):
        """
        判断当前的样本x_i是否满足KKT条件
        :param i:需要判断的样本下标
        :return: True:满足KKT条件；False：不满足KKT条件
        """
        flag = True
        if (self.alpha[i] == 0 and self.labels[i] * self.g[i] < 1-self.eps) \
                or (self.alpha[i] == self.C and self.labels[i] * self.g[i] > 1+self.eps)\
                or (0 < self.alpha[i] < self.C and 1-self.eps < self.labels[i] * self.g[i] < 1+self.eps):
            flag = False
        return flag

    def __check_all_satisfied_KKT(self):
        """判断是否所有样本均满足KKT条件，如果有不满足的，则返回False"""
        flag = True
        s = np.dot(self.alpha.T, self.labels)
        for i in range(self.m):
            if not self.__check_KKT(i):
                flag = False
                break
        return flag

    def __cal_k(self,xi,xj):
        """
        计算核函数
        :param xi:用于计算核函数的样本，xi,i=1,2...,m
        :param xj: 待计算的样本集，在predict中是测试集，在SMO中就是原训练集
        :return: 计算后的核函数结果矩阵，第i列是第i个带计算样本映射后的新特征
        """
        k = np.zeros((xi.shape[0],xj.shape[0]))
        if self.kernel=='linear':
            p = 1  # 线性核函数的超参数
            k = (np.dot(xi,xj.T) + 1) ** p  # 注意，在SMO中，x,xi.T改成xi,x.T没关系，但是在predict中就会出现尺寸问题
        elif self.kernel=='rbf':
            sigma = 0.4  # 高斯核函数的超参数
            for i in range(xi.shape[0]):
                k[i,:] = np.exp(-np.sum((xi[i,:]-xj)**2,axis=1).T/(2*sigma))
        else:
            raise ValueError("kernel must be one of ['lineal','rbf']")
        return k

    def __cal_g(self):
        self.g = np.dot(self.k,self.alpha*self.labels) + self.b

    def __cal_E(self):
        self.E = self.g - self.labels

    def __select_1st_param(self):
        """SMO算法外层循环，选择第一个变量
        如果样本i不满足KKT条件，则dis[i]代表样本i偏离KKT条件的程度；
        如果样本i是满足KKT条件的，则dis[i]是无效值
        :return: 返回选好的第一个参数下标
        """
        dis = self.labels * self.g - 1
        mdis = 0  # mdis表示最偏离KKT条件的程度
        i1 = -1  # i1表示最偏离KKT条件的样本序号
        for i in range(self.m):
            if self.alpha[i] == 0 and dis[i] < -self.eps and -dis[i] > mdis:
                mdis = -dis[i]
                i1 = i
            elif self.alpha[i] == self.C and dis[i] > self.eps and dis[i] > mdis:
                mdis = dis[i]
                i1 = i
            elif 0 < self.alpha[i] < self.C and -self.eps < dis[i] < self.eps and abs(dis[i]) > mdis:
                mdis = abs(dis[i])
                i1 = i
            else:
                continue  # 表示样本满足KKT条件，则直接跳过
        return i1

    def __select_2nd_param(self,i1):
        """SMO算法的内层循环，简单选择对应i1变量的|E[i1]-E[i2]|最大的i2"""
        i2 = -1  # 选择第二个样本的序号
        if self.E[i1]>0:
            i2 = np.argmin(self.E)
        else:
            i2 = np.argmax(self.E)
        return i2

    def __update_new_a1a2(self, i1, i2):
        """更新计算后(截取后)的alpha[i2],再更新alpha[i1]
        :param i1: 选择的第一个参数下标
        :param i2: 选择的第二个参数下标
        eta:计算过程量，eta=K11+K22-2*K12
        newunc_a2:未截取前得到的新alpha[i2]
        tao:约束条件中alpha[i1]*labels[i1]+alpha[i2]*labels[i2] = -sum_{i=3}^m alpha[i]*labels[i] 右侧的常数，
            即tao = -sum_{i=3}^m alpha[i]*labels[i]
        :returns:更新后的参数直接保存在self.alpha[i1],self.alpha[i2]里了
        """
        # 确定alpha的空间范围[L,H]
        eta = self.k[i1,i1] + self.k[i2,i2] - 2 * self.k[i1,i2]
        newunc_a2 = self.alpha[i2] + self.labels[i2] * (self.E[i1] - self.E[i2]) / eta

        if self.labels[i1]!=self.labels[i2]:
            L = max(0,self.alpha[i2]-self.alpha[i1])
            H = min(self.C,self.C+self.alpha[i2]-self.alpha[i1])
        else:
            L = max(0,self.alpha[i2]+self.alpha[i1]-self.C)
            H = min(self.C,self.alpha[i2]+self.alpha[i1])
        if newunc_a2 > H:
            self.alpha[i2] = H
        elif newunc_a2 < L:
            self.alpha[i2] = L
        else:
            self.alpha[i2] = newunc_a2
        tao = -(np.sum(self.labels * self.alpha) - self.labels[i1] * self.alpha[i1] - self.labels[i2] * self.alpha[i2])
        self.alpha[i1] = (tao - self.labels[i2] * self.alpha[i2]) / self.labels[i1]

    def __update_b(self,i1,i2,old_a1,old_a2):
        """更新参数b，更新后的b就是当前迭代的最优参数b
        :params i1,i2: 当前优化的两个参数序号
        :params old_a1,old_a2: alpha[i1],alpha[i2]更新前的数值
        """
        if 0 < self.alpha[i1] < self.C and 0 < self.alpha[i2] < self.C:
            self.b = -self.E[i1] - self.labels[i1] * self.k[i1, i1] * (self.alpha[i1] - old_a1)\
                     - self.labels[i2] * self.k[i2, i1] * (self.alpha[i2] - old_a2) + self.b
        else:
            b1 = -self.E[i1] - self.labels[i1] * self.k[i1, i1] * (self.alpha[i1] - old_a1)\
                 - self.labels[i2] * self.k[i2, i1] * (self.alpha[i2] - old_a2) + self.b
            b2 = -self.E[i2] - self.labels[i1] * self.k[i1, i2] * (self.alpha[i1] - old_a1)\
                 - self.labels[i2] * self.k[i2, i2] * (self.alpha[i2] - old_a2) + self.b
            self.b = (b1 + b2) / 2.

    def __SMO(self):
        """SMO算法主体部分，主要流程是：
        1.初始化(虽然init函数中已完成，但是还是要初始化一遍
            防止用户多次调用SMO，而第二次调用的时候各参数就已经不是初始化的值了；
        2.根据最偏离原则选择第一个参数alpha[i1]
        3.根据max|E[i1]-E[i2]|原则选择第二个参数alpha[i2]
        4.固定其他参数，求解只关于i1,i2两变量的最优化问题，更新alpha[i1]，alpha[i2]
        5.判断是否满足停止条件:1).所有样本都满足KKT条件；2).迭代次数到限制值
            若满足，则当前的self.alpha就是最优解
            否则，重复步骤2~5
        """
        self.alpha = np.zeros((self.m,1))
        self.b = 0
        num_iter = 0
        self.k = self.__cal_k(self.features,self.features)
        self.__cal_g()
        while not self.__check_all_satisfied_KKT() and num_iter < self.maxIter:
            num_iter += 1
            self.__cal_E()
            i1 = self.__select_1st_param()
            i2 = self.__select_2nd_param(i1)
            old_a1 = self.alpha[i1]
            old_a2 = self.alpha[i2]
            self.__update_new_a1a2(i1, i2)
            self.__update_b(i1,i2,old_a1,old_a1)
            self.__cal_g()  # 更新参数后，需要重新计算g值，下次循环中，E值也会随之更新

    def train(self):
    	"""SVM的训练只需要使用SMO算法求出最优参数alpha的序列，
    	即可根据g(x)=K × (alpha · y) + b
    	以及最终分类pred=sign(g(x))得到分类结果"""
        self.__SMO()

    def predict(self,test_x):
        """更新后的参数进行预测，其实只要计算测试集关于训练集的核函数就好了。
        :param test_x: 输入预测样本测试集
        :return: 输出预测结果
        """
        pred = np.dot(self.__cal_k(test_x,self.features), self.alpha * self.labels) + self.b
        pred[pred>=0] = 1
        pred[pred<0] = -1
        pred = pred.astype(np.int8)
        return pred

2.2 实践检验

  实践部分使用经典的鸢尾花数据集，取其中前两种鸢尾花类别进行检验。
  下面贴上导入数据和使用上述自己编写的SVM类进行训练、预测和绘图的代码，仅供大家参考。大家可以自行使用别的数据检测，如有错误欢迎指出。

#######################数据导入部分################################
def data_load(show_data=False):
    name = {'setosa':1, 'versicolor':-1, 'virginica':2}
    data = pd.read_csv("../Data/Iris/iris.csv")
    data = data.drop(["id","Petal.Length","Petal.Width"],axis=1)
    train_X = data.iloc[0:100,0:2].to_numpy()
    train_Y = list(data.iloc[0:100,2])
    train_Y = list(map(lambda x:name[x],train_Y))
    train_Y = np.resize(np.array(train_Y),(len(train_Y),1))

    # 改变训练数据顺序，会产生不一样的结果！！！！
    # random_index = list(range(train_X.shape[0]))
    # random.shuffle(random_index)
    # train_X = train_X[random_index]
    # train_Y = train_Y[random_index]

    if show_data:
        color = {1: 'r', -1: 'g', 'virginica': 'b'}
        plt.figure()
        for i in range(train_Y.shape[0]):
            plt.scatter(train_X[i,0],train_X[i,1],c=color[train_Y[i,0]])
        plt.show()

    return train_X,train_Y  #,test_X,test_Y

#############################训练、预测和绘图的代码#############################
def main():
    # 读取数据
    train_X,train_Y = data_load(False)

    # 训练数据
    svm = SVM(train_X,train_Y,'rbf') 
    svm.train()

    # 用sklearn的svm函数
    # svm = s.SVC()
    # svm.fit(train_X,train_Y)

    # 预测数据并绘制SVM分类图
    x = np.linspace(4,7,50)
    y = np.linspace(1.5,4.5,50)
    xx,yy = np.meshgrid(x,y)
    test_X = np.array([i for i in zip(xx.flat,yy.flat)])
    pred = svm.predict(test_X)

    pred = pred.reshape(xx.shape)
    # 绘制SVM分类后的区域
    color1 = mpl.colors.ListedColormap(['#A0FFA0','#FFA0A0'])
    color2 = {1: 'w', -1: 'k', 'virginica': 'b'}
    plt.figure(figsize=(12,8))
    plt.pcolormesh(xx,yy,pred,cmap=color1)
    # 绘制训练集样本点
    for i in range(train_Y.shape[0]):
        plt.scatter(train_X[i, 0], train_X[i, 1], c=color2[train_Y[i, 0]])
    plt.show()

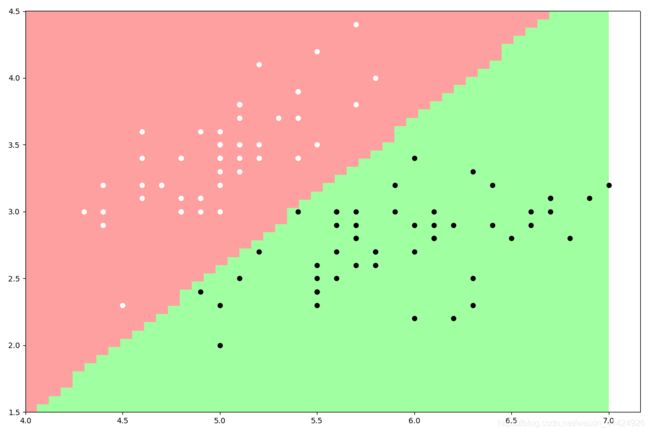
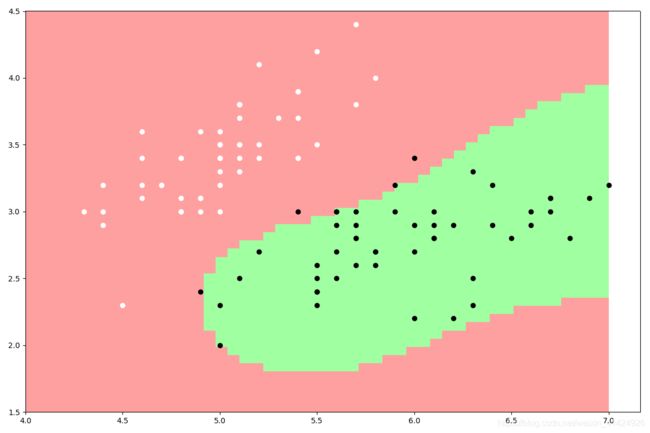
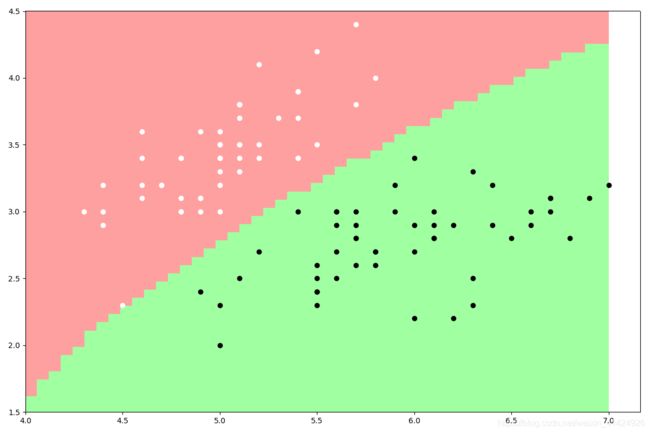
  最终，使用多项式核函数(p=1)、高斯核函数($\sigma =0.4$)以及作为对比使用sklearn的SVM算法，分别得到以下三张分类结果图。读者也可以自行调整超参数试试其他效果。可以看到，sklearn的SVM算法效果明显比自己写的好(这好像是废话，嘿嘿，向大佬低头)，有时间可以看看sklearn中SVM算法的源码，向专业团队学习学习。