王道数据结构代码练习
一、线性表
1. 顺序表上基本操作实现(考试时一定要花时间画出表来分析,就不会错!!)
牢记一点:一定要仔细审题,看清问的是表的位序还是数组下标!
L.data [ ]里面一定是数组下标(人家本身都是个数组了…)
线性表中元素的位序从1开始
而数组中元素的下标从0开始
(1) 顺序表的结构体定义
#define maxSize 100 //定义一个整型常量
typedef struct
{
ElemType data[maxSize]; //存放顺序表中元素
int length; //顺序表长度
}Sqlist; //顺序表结点类型定义
注:考试中常用:
// 定义一个长度为n,表内元素为整数的线性表
int A[maxSize];
int n;
(2)顺序表按位查找
用e返回L中第i (1<= i <= L.length) 个元素的值
int getElem(SqList L, int i, ElemType e)
{
if(i<1 || i>L.length) //i值越界错误,返回0——线性表位序
return 0;
e=L.data[i-1]; //线性表中 ai 对应的元素是L.data[i-1]——数组下标
return 1;
}
(3)顺序表按值查找(顺序查找)
查找第一个元素值等于e的元素,并返回其位序(注意:不是数组下标)
int LocateElem(SqList L, ElemType e)
{
int i;
for(i=0;i<L.length;i++)
if(L.data[i]==e) //L.data[]里放数组下标
return i+1; //位序要 +1
return 0;
}
(4)顺序表插入
列举模拟是最好的理解方式:不懂看王道 P15,脑子里过一遍流程
在顺序表的第 i(1 <= i <= length+1)个位置插入新元素e( 注意审题:i 是表中位序!!)
int insertElem(Sqlist &L, ElemType e, int i)
{
int j;
if(i<1||i>L.length+1) //判断i的范围是否有效
return 0;
if(L.length >= MaxSize) //当前存储空间已满,不能插入
return 0;
for(j=L.length;j>=i;j--) //将第i个元素及之后元素右移 (若i是数组下标,这里就是j>i)
L.data[j]=L.data[j-1];
L.data[i-1]=e; //因为i是表中位序,而 L.data[] 里填的都是数组,对应到数组中要减1 (同样,若题目中i表示数组,这里就直接 L.data[i])
L.length++; //顺序表长增1
return 1;
}
为什么判断一遍 L.length 后还要再判断一遍 MaxSize ?有什么区别?
注意:MaxSize是这段连续空间的大小,而 L.length 是表中实际元素的大小(也就是表的最大下标),这也是为什么插入最后要 L.length++ ,插入前判断两遍是有必要的,第一遍看要插的位置有没有效;第二遍看后面有没有空格让你挪,不够那得用sizeof申请存储空间。
时间复杂度:O(n)
(5)顺序表删除
删除顺序表中第 i(1 <= i <= length)个位置的元素
int ListDelete(SqList &L, int i ,ElemType &e)
{
int j;
if(i<1||i>L.length) //判断i的范围是否有效
return 0;
e=L.data[i-1]; //将被删除的元素赋值给e
for(j=i;j<L.length;j++) //将第i个位置后的元素前移
L.data[j-1]=L.data[j];
L.length--; //顺序表长度减1
return 1;
}
时间复杂度:O(n)
(6)顺序表就地逆置
分析:对称元素交换。线性表(0,1,2…n-1),设表长n,将线性表中第 i 个元素与第 n-i-1 个元素交换。
void Reverse(SqList L){
n=L.length;
for(int i=0;i<n/2;i++){
L.data[i]=L.data[i]+L.data[n-i-1]; //套路:不用另设变量的交换方法
L.data[n-i-1]=L.data[i]-L.data[n-i-1];
L.data[i]=L.data[i]-L.data[n-i-1];
}
}
(7)将x插入到递增有序顺序表中并保持递增有序
采用顺序查找(循环),找到后将右边元素全部右移,再插入
void Insert_Ordered(SqList L,int x){
int i;
if(L.length>=Maxsize)
{
printf("OverFlow");
return;
}
while(i<L.length && L.data[i]<x) i++; //找到插入位置:L.data[i]的值比x大
for(int j=L.length;j>=i;j--) //后面元素全部后移(包括i)
L.data[j+1]=L.data[j];
L.data[i]=x; //将x放入空位
L.length++; //表长加一
}
(8)用顺序表表示集合,实现集合求交集运算
分析:C中元素即是A,B中的公共元素。扫描A中的元素,若A.data[i]与B中某个元素相等,则表示是交集中的元素,放入C中
void Interest(SeqList A, SeqList B, SeqList C)
{
int k=0;
for(int i=0;i<A.length;i++)
{
for(int j=0;j<B.length;j++)
if(A.data[i]==B.data[j])
break;
if(j<B.length)
{
C.data[k]=A.data[i];
k++;
}
}
C.length=k;
}
(9)用顺序表表示集合,实现集合求并集运算
分析:先将A全部复制进C中,扫描B,若B中元素与A中所有元素都不同,则放入C中
void Union(SqList A,SqList B,SqList C){
int k = A.length;
for(int i=0;i<A.length;i++) //将A中元素全部复制进C中
C.data[i]=A.data[i];
for(int i=0;i<B.length;i++){ //用B的元素与A的一一比较,两层循环,B套A
for(int j=0;j<A.length;j++) //遍历找到B中与A中所有元素均不相同的那个元素
if(B.data[i]==A.data[i])
break;
if(j>=A.length){ //若B中某元素与A中所有元素均不相同,则将其放入C中
C.data[k]=B.data[i];
k++;
}
}
C.length=k;
}
(10)约瑟夫环问题
//结构体定义
typedef struct Jonse
{
int data;
struct Jonse *next; //编号(轮到谁)
}Jonse;
//创建约瑟夫环
Jonse * Create(int n) //建立n个结点的单向循环链表函数
{
Jonse *p,*h,*q;
int i;
h=(Jonse *)malloc(sizeof(Jonse)); //为头结点分配空间
p=h;
for(i=1;i<=n;i++)
{
p->data=i; //编号
if(i<n)
{
q=(Jonse *)malloc(sizeof(Jonse)); //创建新的结点
p->next=q;
p=q;
}
}
p->next=h;
return h; //最后返回头结点
}
//打印约瑟夫环上的结点
void ShowList(Jonse *h)
{
Jonse *p;
p=h;
do
{
printf("%d\t",p->data);
p=p->next;
}while(p!=h);
}
//杀人游戏
Jonse* JonseOut(Jonse *h,int n, int m) //n为起点,m为分界点
{
Jonse *p,*q; //q一直指向p的前一个结点
while(p!=p->next) //只要环中还有人
{
for(int k=1;k<m;k++)
{
q=p; //同时往后查找
p=p->next;
}
printf("%d\t",p->data);
//重新构造循环链表
q->next=p->next;
free(p); //释放p结点
p=NULL;
p=q->next; //从下一结点重新开始
}
printf("\nThe winner is %d\n",p->data);
return p;
}
2. 单链表上基本操作实现
(1) 单链表的结构体定义
地址运算符 &:&nurse表示变量nurse的地址。
间接运算符 *:当后跟一个指针名或地址时, * 给出存储在被指向地址中的数值。
例如: val = *ptr; // 将ptr指向的值赋给val (ptr是一个地址)
typedef struct LNode //typedef通俗来说就是给紧跟其后的类型起个别名
{
ElemType data; //数据域(ElemType 的具体类型视题目而定,叫写int写int,叫写char写char
struct LNode *next; //指针域
}LNode, *LinkList; //单链表结点类型定义:*LinkList的意思是LinkList是指向链表结点LNode的指针,LinkList L则表示L是单链表的头
但其实
// 定义一个结点n,下面语法等价
struct LNode n <———————> LNode n
// 定义一个指针p,下面语法等价(第三种最好)
struct LNode *p <———————> LNode *p <———————> LinkList p
注意:指针变量p定义后,并没有存放任何结点的地址,要用malloc动态分配LNode结点大小的存储空间
p = (LinkList)malloc(sizeof(LNode));
p->data = 100; // 表示数据元素
p->next = null; // 表示直接后继的地址
带头结点的链表有什么好处?
(2) 头插法建立单链表
// 从表尾到表头逆向建立单链表L,每次均在头结点之后插入元素
void List_HeadInsert(LinkList &L, ElemType a[],int n)
{
LNode *s, int i;
L=(LinkList)malloc(sizeof(LNode)); //创建头结点
L->next=NULL; //初始为空链表
for(i=0;i<n;i++) //创建a1.a2....an n个结点
{
s=((LNode*)malloc(sizeof(LNode)); //创建新结点
s->data=a[i]; //数据域
s->next=L->next; //将新结点插入表中,L为头指针
L->next=s;
}
}
(3) 尾插法建立单链表
必须新增一个尾节点指针r,始终指向链表的尾节点(更新操作)
// 从表头到表尾正向建立单链表L,每次均在尾结点之后插入元素
void List_TailInsert(LinkList &L, ElemType a[],int n)
{
LNode *s, *r; int i;
L=(LinkList)malloc(sizeof(LNode)); //创建头结点
r=L; //r始终指向尾节点,开始时指向头结点
L->next=NULL;
for(i=0;i<n;i++) //创建a1.a2....an n个结点
{
s=((LNode *)malloc(sizeof(LNode)); //创建新结点
s->data=a[i]; //数据域
r->next=s; //将 *s 插入到 *r 之后
r=s; //更新r
}
r->next=NULL; //最后将尾节点next域置为NULL
}
(4) 单链表按位查找
LNode *GetElem(LinkList &L, int i)
//取出单链表L(带头结点)中第i个位置的结点指针
{
int j=1; //计数,初始值为1
LNode *p=L->next; //头结点指针赋值给p
if(i==0) //i=0,返回头结点
return L;
if(i<1) //无效地址,返回NULL
return NULL;
while(p&&j<i){ //从第1个节点开始找,查找第i个节点
p=p->next;
j++;
}
return p;
}
(5) 单链表按值查找
LNode *LocateElem(LinkList &L, ElemType e)
//查找单链表L(带头结点)中值为e的结点
{
LNode *p=L->next; //头结点指针赋值给p
while(p!NULL&&p->data!=e) //从第1个节点开始找data为e的结点,找不到就一直循环
p=p->next;
return p;
}
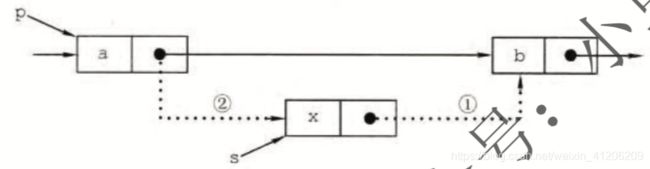
(6)插入结点
p=GetElem(L,i-1); //查找插入位置的前驱结点
s->next=p->next; //右边的是箭头,捏着箭头往回找
p->next=s;
如果要进行前插操作,可以仍然照上面把s后插到p后面,然后将p->data与s->data交换(temp),时间复杂度仍为O(1)
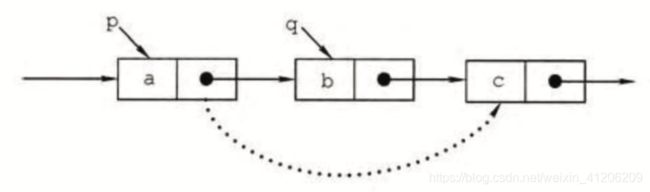
(7)删除结点
p=GetElem(L,i-1); //查找被删除结点的前驱结点p
q=p->next; //令q指向被删除的结点
p->next=q->next; //断开链接
free(q); //释放结点存储空间
如果给定了p,让删除p(没给前驱),可以将p->next->data赋值给p->data,在把p的后继删除,时间复杂度O(1)。
3. 双链表上基本操作实现
(1) 双链表的结构体定义
typedef struct DNode
{
ElemType data; //存放结点数据域
struct DNode *prior,*next; //指向前驱和后继结点的指针
}DNode, *DLinkList; //双链表结点类型定义
4. 栈和队列的应用
(1)括号匹配
思路:遇到左括号入栈,遇到右括号则与栈顶括号比较,匹配则出栈。若栈中无括号匹配或还有未匹配括号,则匹配出错。
bool MatchBrackets()
{
int MAXSIZE=1024; //定义栈最大容量
char s[MAXSIZE];
int top; //栈顶
top=0; //栈初始化
ch=getchar(); //检查括号是否匹配
while(ch!=EOF){
switch(ch){
case'(','[','{':
s[top++]=ch; //所有左括号入栈
break;
case')':
if(top==0 or s[--top]!='(') return false; //栈空或右括号不与栈顶左括号匹配
case']':
if(top==0 or s[--top]!='[') return false;
case'}':
if(top==0 or s[--top]!='{') return false;
}
ch=getchar(); //取下一个字符
}
if (top==0) return true; //正好匹配
else return false; //栈中还有未匹配的左括号
}
5. 链表上基本操作实现
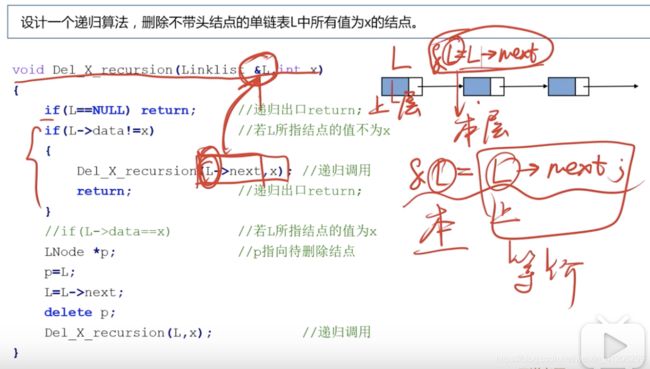
(1) 递归实现单链表L中删除值为x的结点
//草稿
int LocateDelete(LinkList &L, ElemType x)
{
LNode *p=L;
if(p->data==x){ //if会死循环,应该在if里递归,递归里设置出口
q=p;
p=L->next;
free(q);
}
else LocateDelete(p->next)
}
//答案
void Del_X_recursion(LinkList &L, int x){
//递归实现单链表L中删除值为x的结点
if(L==NULL) return; //递归出口return;
if(L->data!=x){ //若L所指结点的值不为x——出口2
Del_X_recursion(L->next,x); //递归调用
return; //递归出口return; 这里的return从最里层开始
}
//if(L->data==x) //若所指结点的值为x,肯定满足,可以注释掉
LNode *p; //p指向待删除结点
p=L;
L=L->next;
delete p; //此处是c++写法,c是free(p);
Del_X_recursion(L,x); //递归调用
}
总结:
-
递归常用套路:把递归出口写在最前面
-
为什么不需要前驱结点?不会断链吗?
不用,因为用了引用,引用就是取别名,即:&p=q是同一个指针,只是名字不同而已;但是若一般的传值:p=q,p和q是两个指针,他们只是指向了同一个元素,但地址不同。
想到与L->next=L->next->next;
把引用看做是结点“亲自走过去”,不会断链。
(2)L为带头结点的单链表,删除L中所有值为x的结点
//解法一:从头到尾遍历
//该算法为无序单链表中删除满足某种条件的所有结点的模板,只要修改if条件,就可以任意指定
void Del_X_1(LinkList &L, ElemType x){
//L为带头结点的单链表,本算法删除L中所有值为x的结点
LNode *p=L->next,*pre=L,*q; //置p和pre的初始值
while(p!=NULL){
if(p->data==x){
q=p; //q用来删除
p=p->next; //p和pre都往后移
pre->next=p;
free(q);
}
else
pre=p; //即:pre=pre->next;
p=p->next;
}
}
//解法二:用尾插法重新建立
void Del_X_1(LinkList &L, ElemType x){
LNode *p=L->next,*r=L,*q; //r指向尾节点,其初始值为头结点
while(p!=NULL){
if(p->data!=x){ //*p结点不为x时将其链接到L尾部
r-next=p;
r=p;
p=p->next;
}
else //*p结点为x时将其释放
q=p;
p=p->next;
free(q);
}
r-next=NULL; //插入结束后置尾节点指针为NULL
}
void Op_Ouput(LinkList &L, ElemType x){
LNode *p=L->next,
}
(3)反向输出单链表
//法一:递归(不改变链表结构)
void R_Print(LinkList &L){
if(L-next!=NULL){
R_Print(L->next);
}
print(L->data);
}
(4)翻转单链表
链表翻转操作的顺序对于迭代来说是从链头往链尾,而对于递归是从链尾往链头。
对于迭代的理解
//法一:迭代:头插法
//将头结点摘下,从第一个节点开始,依次插入到头结点之后,直至最后一个结点为止
void Reverse(LNode *L) //LinkList Reverse(LinkList L)
{
LNode *p,*r;
p=L->next;
L->next=NULL; //把头结点摘下来(作为一个新表)
while(p!=NULL){
r=p->next; //r用来暂存p的后继结点,防止断链
p->next=L->next; //把p插到新表L的头结点和首节点之间
L->next=p; //使L的首节点一路跟着p完后走
p=r; //p返回原链表中暂存,即p的后继
}
}
//法二:递归:指针反指
//位置不动,改指向。也就是将后一结点指向前一结点,注意每次反转后要将原链表中前一个结点的指针域置空,表示将原链表中前一个结点指向后一个结点的指向关系断开,不断开会形成环。
ListNode *Reverse(LNode *L){
//递归出口
if(L==NULL||L->next==NULL)
return L;
else
{
ListNode *newL=Reverse(L->next); //递归:从后往前翻转
L->next->next=head; //将后一结点指向前一结点
L->next=NULL; //原链表中前一节点和后一节点的指向关系断开
return newL; //新链表头永远指向的是原链表的链尾
}
}
//法三:迭代:指针反指
ListList Reverse(LinkList &L){ //返回头结点
LNode *pre,*p=L->next,*r=p->next; //定义前驱,当前及后继结点
p->next=NULL; //设置初始值
while(r!=NULL){ //循环知道r为空,p为最后一个结点
pre=p; //3个指针依次后移
p=r;
r=r->next;
p->next=pre; //指针反指,让p指向其前驱
}
L->next=p; //处理最后一个结点,经过上面循环,此时最后一个节点是p,让头结点直接指向p
return L;
(5)合并两个单链表并保持递增有序
void Merge_L(LinkList &La,LinkList &Lb){
LNode *pa,*pb,*r; //套路:链表初始化包括两步:定义指针——该指针指向首元结点(赋值)
pa=La->next; //pa指向La的首元结点
pb=Lb->next; //q指向Lb的首元结点
Lc=r=La; //用La的头结点作为Lc的头结点
while(pa&&pb){
if(pa->data < pb->data){ //La的元素小
r->next=pa; //r指向La的元素
r=pa; //r,pa都右移
pa=pa->next;
}
else{ //Lb的元素小
r->next=pb; //r指向Lb的元素
r=pb; //r,pb都右移
pb=pb->next;
}
}
if(pa) //插入剩余段,也可以用条件判断来写:r->next = pa?pa:pb
r->next=pa;
else
r->next=pb;
return La;
}
(6)合并两个递增有序单链表(带头结点),并改为递增有序,并要求用原两个单链表的结点存放归并后的单链表
与前一题比较,采用头插法,不用新创建一个链表。
分析:均从第一个节点起两两比较,将小节点头插法插入链表。因为比较结束,可能有一个链表非空,此时用头插法将剩下节点一次插入链表即可。
void Merge_L_R(LinkList &La, &Lb){
LNode *pa,*pb,*r;
pa=La->next; //pa指向La的首元结点
pb=Lb->next; //pb指向Lb的首元结点
La->next=NULL; //用La作为结果链表
while(pa&&pb){
if(pa->data < pb->data){ //La的元素小
r=pa->next; //r暂存pa后继结点,以防断链
pa->next=La->next; //这两步是头插法操作,背熟!
La->next=pa;
pa=r; //用r恢复pa为当前待比较结点
}
else{ //Lb的元素小
r=pb->next;
pb->next=Lb->next;
Lb->next=pb;
pb=r;
}
}
if(pa) //插入剩余段,注:不改变顺序的话直接插入尾部就行,但是逆序还要再用一次头插法(挨个处理)
pb=pa; //简化if/else操作
while(pb){ //头插法
r=pb->next;
pb->next=Lb->next;
Lb->next=pb;
pb=r;
}
}
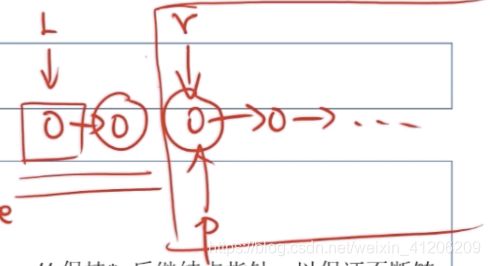
(7)在带头结点的单链表L中删除一整个最小值结点的高效算法(假设最小值唯一)
分析:采用两组指针,p从头至尾扫描单链表,用minp保留保存值最小的结点(初始为p),扫描过程中若出现p->data小于minp,则把p赋值给minp。
Delete_Min_L(LinkList &L){
LNode *pre=L,*p=pre->next; //p为工作指针,pre指向其前驱
LNode *minpre=pre,*minp=p; //保存最小值结点及其前驱
while(p!=NULL){
if(p->data < minp->data){
minp=p;
minpre=pre;
}
pre=p; //继续扫描下一节点
p=p->next;
}
minpre->next=minp->next; //删除最小值结点
free(minp);
return L; //返回头结点
}
(8)实现单链表元素递增有序
分析:直插法的思想(前有序,后无序的一个一个往前找位置插)
void Sort(LinkList &L){
LNode *p=L->next,*pre; //定义前驱,当前,后继结点(保证不断链)
LNode *r=p->next;
p->next=NULL; //构造只含一个数据节点的有序表
p=r; //从后面开始找
while(p!=NULL){
r=p->next //保存p的后继结点指针
pre=L;
while(pre->next=NULL&&pre->next->data < p->data) //在有序表中查找插入*p的前驱结点*pre
pre=pre->next;
p->next=pre->next; //插入操作
pre->next=p;
p=r; //扫描原单链表中剩下节点
}
}
(9)删除无序表中介于给定的两个值之间的所有元素
void RangeDelete(LinkList &L,int min,int max){
LNode *pre=L,p=L->next; //p是检测指针,pre是其前驱
while(p!=NULL){
if(p->data>min && p->data<max){ //寻找到被删除结点,删除
pre->next=p->next;
free(p);
p=pre->next;
}
else{ //否则寻找被删除结点
pre=p;
p=p->next;
}
}
}
(10)找出两个单链表的公共结点
分析:分别遍历两个链表得到长度,并求出长度之差。先在长链表上遍历长度之差个节点之后,再同步遍历两个链表,直到相同结点,或一直到链表结束。
空间复杂度O(1)
时间复杂度O(len1+len2)
注意:由于每个单链表只有一个next域,因此从第一个公共结点开始,之后结点都是重合的,Y型

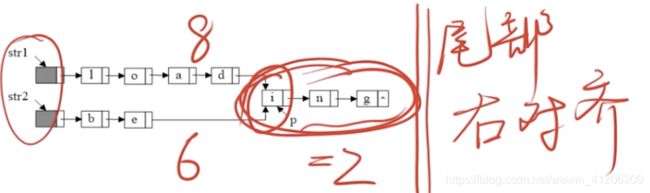
关键要找到第一个公共结点:

LinkList ComNode(LinkList &L1, LinkList &L2){ //返回指向第一个公共结点的指针
int len1=Length(L1),len2=Length(L2),dist; //计算两个链表表长,定义dist用来记录长度差
LinkList longList,shortlist; //两个指向长链表和短链表的指针
if(len1>len2){ //L1更长
longlist=L1->next;
shortlist=L2->next;
dist=len1-len2;
}
else{
longlist=L2->next;
shortlist=L1->next;
dist=len2-len1;
}
while(dist--) //遍历知道两个链表的结点处于同一起跑线上
longlist=longlist->next;
while(longlist!=NULL){
if(longlist==shortlist) //找到第一个公共结点
return longlist;
else{
longlist=longlist->next;
shortlist=shortlist->next;
}
}
return NULL; //无公共节点
}
(11)按递增顺序输出单链表中的数据元素
分析:不给使用数组作为辅存空间的话,只能从头遍历了,每趟遍历找出整个链表中最小的元素,输出并释放结点空间,直至链表为空,最后释放头结点,时间复杂度O(n^2)
void Min_Delete(LinkList &head){
while(head->next!=NULL){ //循环到仅剩头结点
LNode *minpre=head; //minpre为元素最小值结点的前驱结点的指针
LNode *p=head->next; //p为工作指针
//找出现在单链表中最小值
while(p->next!=NULL){ //至少剩余两个数据结点:否则比较无意义
if(p->next->data < minpre->next->data)
minpre=p; //更新最小值前驱
p=p->next;
}
print(minpre->next->data); //输出元素最小值结点的数据
u=minpre->next; //删除元素值最小的结点,释放结点空间
minpre->next=u->next;
free(u);
}
free(head); //释放头结点
}
(12)将表中结点按奇偶性分解到表A,B中

分析:设置一个变量保存访问序号(初始值为0),每访问一个结点序号自动加1,然后由奇偶性再插入。
时间复杂度:O(n)
LinkList DisCreat_1(LinkList &A){ //返回B表头(A已知)
int i=0; //原表中访问序号
LinkList B=(LinkList)malloc(sizeof(LNode)); //创建B表表头 (用原表作为A表)
B->next=NULL; //B表初始化
LNode *ra=A,*rb=B; //ra,rb分别指向将创建的A,B表的表尾(尾插法:正序)
LNode *p=A->next; //工作指针,用来遍历原表
A->next=NULL; //置空新的A表(此处数据会不会全部消失?不会,因为只是A的头结点和下一个结点之间断开链接,但是提前用p指向了A->next,所以只是相当于扯下了头结点)
while(p!=NULL){
i++; //序号加1
if(i%2==0){ //偶序
rb->next=p; //在B表尾插入新结点
rb=p; //rb指向新的尾节点
}
else{
ra->next=p; //在A表尾插入新结点
ra=p; //ra指向新的尾节点
}
p=p->next; //p继续处理下一结点
}
ra->next=NULL;
rb->next=NULL;
return B;
}
(13)用就地算法实现将线性表拆分为两个表
就地算法:指的是直接修改输入数据而不是将输入数据复制一份处理之后再覆盖回去。
此处共需要保存3个链表指针,p工作指针 , ra, q是为了恢复时不断链

LinkList DisCreat_2(LinkList &A){
LinkList B=(LinkList)malloc(sizeof(LNode));
B->next=NULL; //B表初始化
LNode *p=A->next, *q; //p为工作指针
LNode *ra=A; //ra始终指向A的尾结点
while(p!=NULL){
ra->next=p; //ra,p一开始都指向真正工作结点的前一结点
ra=p; //开始工作,开始后移
p=p->next;
q=p->next; //q暂存p的后继
p->next=B->next; //头插法
B->next=p;
p=q; //恢复到原表链接
}
ra->next=NULL; //因为到an时,此时q还保存了一个空指针
return B;
}
(14)删除一个有序表中数值相同的元素
分析:若节点值域等于后继的值域,则删除后继,否则继续右移。
void Del_Same(LinkList &L)
{
LNode *p=L->next,*q; //定义工作结点和后继结点
if(p==NULL)
return;
while(p->next!=NULL) //因为头结点不存数据,从首节点开始循环
{
q=p->next; //先保存p的后继结点
if(p->data==q->data) //找到重复结点的值
{
p->next=q->next;
free(q);
}
else
p=p->next;
}
}
(15)产生有序单链表A,B公共元素的单链表C
分析:从A,B首元素依次比较,
若元素值不相等,则值小的指针往后移,
若元素值相等,则创建一个值等于这个值的新节点,再用尾插法插到新链表中,A,B两个表指针都往后移,
直到其中一个链表遍历到表尾。
时间复杂度:O(n),n为较短链表 空间:O(n)
void Get_Common(LinkList A,LinkList B)
{
LNode *p=A->next,*q=B->next,*r,*s; //p,q指向A,B首结点,r指向C的表尾,s用来复制结点(创建新节点)
LinkList C=(LNode *)malloc(sizeof(LNode)); //创建表C
r=C; //r始终指向C的表尾
while(p!=NULL&&q!=NULL)
{
if(p->data<q->data) //A表元素较小(谁小移谁,大的等小的)
p=p->next;
else if(p->data>q->data)
q=q->next;
else{ //找到公共元素结点
s=(LNode *)malloc(sizeof(LNode));
s->data=p->data; //复制产生结点*s
r->next=s; //尾插法把s链接到C的尾部
r=s;
p=p->next; //两表都往后移一位
q=q->next;
}
}
r->next=NULL; //置C尾节点的指针为空
}
(16)求两个单链表的交集
分析:采用归并的思想,设置两个工作指针pa,pb,对两个链表进行扫描,当出现元素值相等时,将A中节点链接到结果表,其余释放,直至一个链表全部遍历完,释放另一个表中剩余节点。
LinkList Union(LinkList &La,LinkList &Lb)
{
pa=la->next;pb=lb->next;
pc=la; //始终指向新链表的尾部
while(pa&&pb)
{
if(pa->data==pb->data)
{
pc->next=pa; //下面3步:把pa摘下来放到pc上
pc=pa;
pa=pa->next;
u=pb; //B中节点释放
pb=pb->next;
free(u);
}
else if(pa->data<pb->data) //A小,A后移
{
u=pa;
pa=pa->next;
free(u);
}
else //B小,B后移
{
u=pb;
pb=pb->next;
free(u);
}
}
//剩余一个表则全部释放
while(pa)
{
u=pa;
pa=pa->next;
free(u);
}
while(pb)
{
u=pb;
pb=pb->next;
free(u);
}
pc->next=NULL; //注意:千万别漏!pc此时还指向A/B表剩余节点,所以必须置空
free(lb)
return la;
}
(17)判断序列B是否为A的连续子序列(无头结点)
分析:从两链表的首节点开始比较,相等则后移,不等则A从上次开始比较的后继开始,B仍从首节点开始。直到B到表尾表示匹配成功,A到尾而B未到则失败。
设置一个记录每次A开始的结点。
时间复杂度:O(n*m)
int Pattern(LinkList &A,LinkList &B) //0失败,1成功
{
LNode *p=A;
LNode *pre=p; //pre记住每趟比较中A链表的开始节点
LNode *q=B;
while(p&&q)
{
if(p->data==q->data) //结点值相同
{
p=p->next;
q=q->next;
}
else //失败
{
pre=pre->next;
p=pre; //A新的开始比较结点
q=B; //q还是从B的首节点开始
}
}
if(q==NULL) //B空,匹配成功
return 1;
else
return 0;
}
(18)判断带头结点的循环双链表是否对称
分析:
思路一——两个指针,一个从头到尾扫描,一个从尾到头扫描,终止条件:发现二者不对称或者比较到中点代表即对称。
如何确认比较到中点?1:同一结点 or 相邻结点 2:提前遍历一遍进行记数
思路二——遍历一遍,数组记忆所有顶点然后再进行判断
int Sym(DLinkList &L)
{
DNode *p=L->next,*q=L->prior //两头工作指针(头、尾)
while(p!=q&&q->next!=p) //是否指向同一结点(奇),或者相邻(偶)
if(p->data==q->data) //所指结点值相同则继续比较
{
p=p->next;
q=q->next;
}
else
return 0;
return 1; //对称
}
(19)将循环链表h2链接到h1之后,且仍保持循环链表
分析:先循环遍历找到两个单链表的尾指针,再进行缝合
LinkList Link(LinkList &h1,LinkList &h2)
{
LNode *p,*q; //分别指向两个链表的尾指针
p=h1; //循环单链表找尾指针的操作
while(p->next!=h1)
p=p->next;
q=h2;
while(q->next!=h2)
q=q->next;
p->next=h2; //h2的头结点指向h1的尾节点
q->next=h1; //h2的尾节点指向h1的头结点
return h1;
}
(20)每次删除循环单链表中的最小元素,直到链表空为止
思想:每循环一次查找一个最小值点并删除它,最后删除头结点。两层循环
void Delete_All(Linklist &L)
{
LNode *p,*pre,*minp,*minpre; //定义结点
while(L->next!=L) //循环单链表非空
{
p=L->next;pre=L;
minp=p;minpre=pre;
while(p!=L) //循环一趟
{
if(p->data<minp->data)
{
minp=p;
minpre=p;
}
//为保证每次判断完最小后,都能再判断一次表长,右移操作要放在外面
pre=p;
p=p->next;
}
printf("%d",minp->data); //输出最小结点元素
minpre-next=minp->next; //删除最小值点
free(minp);
}
free(L); //释放头结点
}
(21)在双链表中进行按值查找,查找成功则该节点的访问频度域值加一,最后将该节点按频度递减插入链表中适当位置(同频度最近访问的在前)。
思想:现在双链表中进行按值查找,查到后将该节点从链表上摘下来,然后以频度作为条件,向前查找一个频度比它大的结点,插在该节点之后。
DLinkList Locate(DLinkList &L,ElemType x)
{
DNode *p=L->next,*q; //定义双向链表头结点即工作结点p,q为p的前驱,用于查找插入位置
while(p&&p->data!=x) //链表非空且值不等,则完后移
p=p->next;
if(!p)
{
printf("不存在值为x的结点\n");
exit(0);
}
else
{
p->freq++; //令元素值为x的结点的频度域加一
p->pred->next=p->next; //将p从双向链表上摘下来(删除结点p)
p->next->pred=p->pred;
q=p->pred; //找到p的插入位置
while(q!=L&&p->freq>=q->freq)
q=q->pred;
p->next=q->next; //插入p节点
q->next->pred=p;
p->pred=q;
q->next=p;
}
return p; //返回值为x的结点的指针
}
(22)查找链表的倒数第k个结点,并输出该结点的值。
思想:定义两个指针变量p,q,初试值指向首节点,p指针随链表移动;但p指针移动到第k个节点时,q指针开始与p指针同步移动,直到p指针移动到表尾,此时q指针所指结点即为倒数第k个节点。此过程仅对链表扫描一次。
int Search_k(LinkList L,int k)
{
LNode *p=L->next, *q=L->next; //定义p,q指向首节点
int count=0;
while(p!=NULL) //链表非空
{
if(count<k) count++; //count
else q=q->next; //否则,p,q同时移动
p=p->next;
}
if(count<k) //k超过链表长度,查找失败
return 0;
else
{
printf("%d",q->data);
return 1;
}
}
(23)找共同后缀的起始地址

注:题目的含义是该结构已经存在,让你去判断起始位置在哪,而不是给你两个单词序列,让你去判断起始位置。
同一个结点:并不是字母相同,而是地址相同,即上一个结点指向这个结点的指针相同(指针就是地址)
时间复杂度:O(len1+len2) 或者 O(max(len1,len2)
LNode *Find_1st_Common(LinkList str1,LinkList str2)
{
int len1=Length(str1),len2=Length(str2); //获取两个单词的长度 O(n)
LNode *p,*q; //定义p,q两个指针用于对齐
for(p=str1;len1>len2;len1--) //使p所指向的链表与q所指向的链表等长
p=p->next;
for(q=str2;len1<len2;len2--) //使p所指向的链表与q所指向的链表等长
q=q->next;
while(p->next!=NULL&&p->next!=q->next) //查找共同后缀的起始结点 O(len1+len2)
{
p=p->next; //两指针同步移动
q=q->next;
}
return p->next; //注意:不是p
}
(24)
算法的核心在于:使用辅助数组记录链表中已出现的值,从而只用对链表进行一次扫描。由于|data| 空间复杂度:O(n) 分析:出队在链头进行,相当于删除开始节点,入队在链尾进行,相当于在终端结点后面再插入一个结点。不带头结点,所以要考虑空表的特殊情况 分析:马鞍点即矩阵 A[N][M] 中第i行元素的最小值,又是第j列元素的最大值 时间复杂度:O(MN+N^2)=O(N方) 分析:首先将根节点入队,然后从队头取一个元素,每取一个元素,执行:
时间复杂度:O(m)void func (LNode h,int n)
{
LNode p=h,r;
int *q,m; //q用于存放数组
q=(int *)malloc(izeof(int)*(n+1)); //申请n+1个位置的辅助空间
for(int i=0;i<n+1;i++) //数组元素初始值置0
q[i]=0;
while(p->next!=NULL)
{
m=p->next->data>0? p->next->data:-p->next->data //取绝对值
if(q[m]==0) //判断该节点的data是否已经出现过
{
q[m]=1; //首次出现
p=p->next; //继续处理下一结点
}
else //重复出现
{
r=p->next;
p->next=r->next; //删除
free(r);
}
}
}
二、栈和队列
(1)两栈共享存储空间的存储结构上的入栈算法和出栈算法
//结构体定义
#define STACKSIZE 100
typedef struct BothStack
{
int data[STACKSIZE];
int top1;
int top2;
}BothStack;
//初始化
void InitBothStack(BothStack S)
{
S.top1=-1;
S.top2=STACKSIZE;
}
//入栈
void PushBothStack(BothStack S, int i, int x)
{
if(i!=1||i!2) //即不入1号,也不入2号
printf("Input error");
if(S.top1==S.top2-1)
printf("Stack Overflow");
else
{
if(i==1)
S.data[++S.top1]=x;
if(i==2)
S.data[++S.top2]=x;
}
}
//出栈
int PopBothStack(BothStack S, int i)
{
if(i==1)
if(S.top1==-1)
{
printf("Stack is empty");
return -1;
}
else
return S.data[S.top1--];
if(i==2)
if(S.top2==STACKSIZE)
{
printf("Stack is empty");
return -1;
}
else
return S.data[S.top2++];
else
{
printf("Input error");
return -1
}
}
(2)不带头结点,只有尾指针的循环链表表示的队列的入队和出队操作
void Enqueue(QNode *rear ,ElemType x)
{
s=(QNode)malloc(sizeof(QNode)); //建立新结点
s->data=x;
if(rear==NULL) //空表
{
rear=s;
rear->next=s;
}
else //链表不为空
{
s->next=rear->next; //尾插法
rear->next=s;
rear=s;
}
}
void Dequeue(QNode *rear)
{
QNode * s;
if(rear==NULL)
printf("already empty");
else
{
s=rear->next;
if(s==rear) //若原队列只有一个结点,则删除后为空
rear==NULL;
else
rear->next=s->next;
free(s);
}
}
(3)把十进制转换为二至九进制质安监的任意进制数输出——栈
void Decimaltor(int num, int r)
{
int top,k;
int S[100];
top=-1;
while(num!=0)
{
k=num%r;
S[++top]=k;
num=num/r;
}
while(top!=-1)
printf(S[top--]);
}
(4)马鞍点算法——矩阵
void Andian(int A[][],int M,int N)
{
int i,j,d;
for(i=0;i<N;i++)
{
d=A[i][0]; //d为第i行的第一个值
k=0;
for(j=1;i<M;j++)
if(A[i][j]<d)
{
d=A[i][j];
k=j; //A[i][k]即为第i行中的最小值
}
for(j=0;i<N;j++)
if(A[j][k]>d)
break;
if(j==N)
printf("Andian point is %d\n",A[j][k]);
}
}
三、树
(1)二叉链表存储二叉树的先序、中序、后序遍历算法——递归实现
typedef struct BiNode
{
ElemType data;
BiNode * lchild, *rchild;
}BiNode;
//二叉树先序遍历递归算法
void PreOrder(BiNode * root)
{
if(root==NULL) return;
visit(root);
PreOrder(root->lchild);
PreOrder(root->rchild);
}
//二叉树中序遍历递归算法
void InOrder(BiNode * root)
{
if(root==NULL) return;
InOrder(root->lchild);
visit(root);
InOrder(root->rchild);
}
//二叉树后序遍历递归算法
void PostOrder(BiNode * root)
{
if(root==NULL) return;
PostOrder(root->lchild);
PostOrder(root->rchild);
visit(root);
}
(2)非递归实现二叉树的遍历(先、中、后)——借助栈
/*
中序非递归遍历
指针从p开始,沿左子树深入,每深入一个结点就入栈该结点,
直至左分支为空时,返回,即出栈,出栈同时访问该节点,同时从此结点的右子树继续深入,
直至最后从根节点的右子树返回则结束。
*/
//完整版
void InOrder(BiTree bt)
{
BiTree S[MAXSIZE],p=bt; //定义栈
int top==-1; //初始化
if(bt==NULL) return; //空二叉树,遍历结束
while(p||top==0) //指针存在,栈非空
{
if(p)
{
/*
先序遍历就现在这里访问p:
visit(p->data);
*/
if(top<MAXSIZE-1) //栈未满则将当前指针p入栈
S[++top]=p;
else
{
printf("栈溢出\n");
return;
}
p=p->lchild; //指针指向p的左孩子结点
}
else
{
p=S[--top]; //弹出栈顶元素
visit(p->data); //访问p结点
p=p->rchild; //指向p的右孩子结点
}
}
}
//简洁版
void InOrder(BiTree bt)
{
InitStack(S);
p=bt;
while(p||!StackEmpty(S))
{
if(p)
{
//先序:visit(p);
Push(S,p);
p=p->lchild;
}
else
{
Pop(S,p);
visit(p);
p=p->rchild;
}
}
}
/*
后序非递归遍历
顺序还是按中序的顺序,只是分别从左子树和右子树共两次返回根节点,只有从右子树返回时才访问根节点,所以需要增加一个栈标记到达结点的次序。
注:后序非递归遍历时,栈中保留的是当前结点的所有祖先,在和祖先有关的算法中十分有用。
*/
//简洁版
void PostOrder(BiTree bt)
{
InitStack(S);
InitStack(tag);
p=bt;
while(p||!StackEmpty(S))
{
if(p)
{
Push(S,p); //第一次入栈
Push(tag,1);
p=p->lchild;
}
else
{
Pop(S,p)
Pop(tag,f);
if(f==1)
{
Push(S,p); //第二次入栈
Push(tag,2);
p=p->rchild;
}
else //第二次出栈
{
visit(p);
p=NULL; //为使下一步能继续退栈
}
}
}
//完整版
void PostOrder(BiTree bt)
{
BiTree S[MAXSIZE]; //初始化栈S
S.top==-1;
BiTree tag[1]; //始化栈tag
tag.top==-1;
p=bt;
if(bt==NULL) return; //空二叉树,遍历结束
while(p||S.top==0) //指针存在,栈非空
{
if(p)
{
if(S.top<MAXSIZE-1) //栈未满则将当前指针p入栈
S[++S.top]=p;
else
{
printf("栈溢出\n");
return;
}
if(tag.top==0) //标记第一次入栈
tag[++tag.top]=1;
p=p->lchild; //指针指向p的左孩子结点
}
else
{
p=S[--S.top]; //先出栈最左结点
f=tag[--tag.top];
if(f==1) //代表从左子树返回,此时不能访问根节点,需二次入栈,找右子树
{
if(S.top<MAXSIZE-1)
S[++S.top]=p;
else
{
printf("栈溢出\n");
return;
}
if(tag.top==0) //标记第二次入栈
tag[++tag.top]=2;
p=p->rchild; //指针指向p的左孩子结点
}
else //从右子树返回(二次出栈),访问根节点,p转上层
{
visit(p->data);
p=NULL;
}
}
}
}
(3)二叉树按层次遍历算法
执行至队列为空。//采用顺序队列(非循环),假定不上溢
void LeverOrder(BiNode * root)
{
BiNode * Q[MAXSIZE]; //定义队列
BiNode * binode;
int front=0,rear=0;
if(root==NULL) return; //空二叉树,遍历结束
Q[++rear]=root; //根节点入队
/*
若为循环队列,此处改为:
Q[rear]=root; //根节点入队
rear=(rear+1)%MAXSIZE;
*/
while(rear!=front) //队列不空,继续遍历,否则遍历结束
{
binode=Q[++front]; //出队
/*
同样,若为循环队列,应改为:
binode=Q[front];
front=(front+1)%MAXSIZE;
*/
visit(binode); //访问出队元素
if(binode->lchild!=NULL) //左子树结点非空,入队
Q[++rear]=binode->lchild;
if(binode->rchild!=NULL) //右子树结点非空,入队
Q[++rear]=binode->rchild;
}
}
(4)二叉树链表存储二叉树,要求不使用全局变量,求叶子总数的递归算法、结点总数的递归算法、整个二叉树深度的递归算法。
//叶子总数的递归算法
int LeafCount(BiNode * root)
{
if(root==0)
return 0;
else
{
if(root->lchild==0 && root->rchild==0)
return 1;
else
return LeafCount(root->lchild)+LeafCount(root->rchild);
}
}
//结点个数
int NodeCount(BiNode * root)
{
if(root==0)
return 0;
else
return(1+NodeCount(root->lchild)+NodeCount(root->rchild));
}
//二叉树深度
int Depth(BiNode * root)
{
if(root==0)
return 0;
else
return(1+max(Depth(root->lchild)+Depth(root->rchild)));
}
(5)二叉排序树常采用二叉链表存储,写出交换左右子树的算法
void Exchange(BiNode * root)
{
BiNode temp;
if(root)
{
Exchange(root->lchild);
Exchange(root->rchild);
temp=root->lchild;
root->lchild=root->rchild;
root->rchild=tempt;
}
}
(6)二叉排序树的插入和构造算法
//二叉排序树的插入算法
void InsertBST(BiNode * root ,BiNode *s)
{
if(root==NULL) //二叉树为空,则直接将插入节点作为根节点
root=s;
else
if(s->data<root->data)
InsertBST(root->lchild,s);
else
InsertBST(root->rchild,s);
}
//二叉排序树的构造算法
void BiSortTree(BiNode * root ,int r[] ,int n)
{
for(int i=0;i<n;i++)
{
s=(BiNode *)malloc(sizeof(BiNode)); //创建节点
s->data=r[i];
s->lchild=s->rchild=NULL;
InsertBST(root,s); //调用二叉排序树插入函数
}
}
(7)二叉排序树搜索的递归和非递归算法
//递归
BiNode SearchBST(BiNode * root ,ElemType x)
{
if(root==NULL) //二叉树为空
return 0;
else if(root->data==x)
return root;
else if(x<root->data)
return SearchBST(root->lchild,x);
else
return SearchBST(root->rchild,x);
}
//非递归——用循环
BiNode SearchBST(BiNode * root ,ElemType x)
{
p=root;
while(p)
{
if(p->data==x)
return p;
else if(x<p->data)
p=p->lchild;
else
p=p->rchild;
}
return 0; //查找失败
}
五、图
六、查找
七、排序