考研数据结构考点之排序

8.1 排序的基本概念

1. 排序算法的评价指标
   1. 时间复杂度
   2. 空间复杂度
   3. 稳定性；是指两个值相等的关键字经过排序后相对位置是否发生变化，没有变化是稳定的，否则不稳定；
2. 排序算法的分类

8.2 插入排序

8.2.1 直接插入排序

空间复杂度 O(1)
最好时间复杂度(全部有序) O(n)
最坏时间复杂度(全部逆序) O(n²)
平均时间复杂度 O(n²)
算法稳定性：稳定
适用性：顺序存储或链式存储都可以
在元素序列基本有序的前提下，效率还是很高的

8.2.2 折半插入排序

空间复杂度 O(1)
平均时间复杂度 O(n²)
算法稳定性：稳定
适用性：顺序存储结构
对于数据量不很大的排序表，折半插入排序往往能表现出很好的性能

8.2.3 希尔排序

希尔排序也被称为“缩小增量排序”
设置一个增量d，即相隔d个位置的元素为一个子表，先让每个子表的元素相对有序，然后让d逐渐减小为1；
希尔排序每趟并不产生有序区
空间复杂度 O(1)
最坏时间复杂度 O(n²) -----让增量d最初便等于1，相当于直接插入排序的最坏
平均时间复杂度 O(n1.3)------当n在某个范围内时，大约是…
算法稳定性：不稳定
适用性：仅适用于顺序存储结构的线性表

8.3 交换排序

8.3.1 冒泡排序

从后往前（或从前往后）两两比较相邻元素的值，若为逆序(A[j-1]>A[j])，则交换；最多只需n-1趟；
空间复杂度 O(1)
最好时间复杂度(全部有序) O(n)
最坏时间复杂度(全部逆序) O(n²)

• 元素全部逆序时，移动次数是比较次数的3倍；
• 因为每比较1次都会交换1次；每交换一次就会移动元素3次（ temp=A[j]; A[j]=A[j-1]; A[j-1]=temp; ）
• 即比较次数=n(n-1)/2；移动次数=3n(n-1)/2；

平均时间复杂度O(n²)
算法稳定性：稳定
适用性：顺序表、链表都可以
冒泡排序每一趟排序结束后产生的有序子序列一定是全局有序的

8.3.2 快速排序

代码实现：

int Partition(ElemType A[],int low,int high){
    //pivot(支点、枢轴)
    ElemType pivot=A[low];
    while(low<high){
        while(A[high]>=pivot&&low<high)
            high--;
        A[low]=A[high];
        while(A[low]<=pivot&&low<high)
            low++;
        A[high]=A[low];
    }
    A[low]=pivot;
    return low;
}

//初始low=0;high=n-1;
void QuickSort(ElemType A[],int low,int high){
    if(low<high){
        int pivotpos=Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
    }
}

在快速排序过程中，并不产生有序子序列，但每次划分后会将枢轴(基准)元素放到其最终的位置上。

效率分析

时间复杂度 = O(n*递归层数)
空间复杂度 = O(递归层数)
递归层数相当于快速排序过程中形成的分析树(二叉排序树)的高度
即 最好情况下的递归层数 = 二叉排序树的最小高度 = log2(n+1) (向上取整)
最好情况下的递归层数 = 二叉排序树的最大高度 = n ；
故

	时间复杂度	空间复杂度
最好情况	O(nlog2n)	O(log2n)
最坏情况	O(n²)	O(n)

快速排序平均情况下的运行时间与其最好情况下的运行时间很接近，而不是接近其最坏情况下的运行时间；
故 平均时间复杂度=O(nlog2n) 平均空间复杂度O(log2n)
算法稳定性：不稳定
快速排序是所有内部排序算法中平均性能最优的排序算法
注：“一趟"排序 == ? 一次"划分” 要看报考大学历年真题中是如何处理的？

8.4 选择排序

8.4.1 简单选择排序

每次循环找出无序序列中最小的元素，与无序序列的第一个位置元素进行交换，然后无序序列的起始位置向后移，有序序列长度加一；
空间复杂度 O(1)
元素移动的次数很少，不会超过3(n-1)，最好的情况是移动0次
元素间比较的次数与序列的初始状态无关，始终是n(n-1)/2，因此时间复杂度始终是O(n²)
最好时间复杂度 O(n²)
最坏时间复杂度 O(n²)
平均时间复杂度 O(n²)
算法稳定性：不稳定
适用性：顺序表、链表都可以

8.4.2 堆排序

代码实现：

typedef int ElemType;
void Swap(int &a,int &b){
    int temp=a;
    a=b;
    b=temp;
}

//将以k为根的子树调整为大根堆
void HeadAdjust(ElemType A[],int k,int len){
    A[0]=A[k];
    for(int i=2*k;i<=len;i=i*2){
        if(i<len&&A[i]<A[i+1])
            i++;
        if(A[i]<=A[0])
            break;
        else{
            A[k]=A[i];
            k=i;
        }
    }
    A[k]=A[0];
}

//建立大根堆，最后排序完成,序列元素升序排列
void BuildMaxHeap(ElemType A[],int len){
    for(int i=len/2;i>0;i--){
        HeadAdjust(A,i,len);    //从以最后一个非叶结点为根的子树开始调整
    }
}
void HeapSort(ElemType A[],int len){
    BuildMaxHeap(A,len);    
    for(int i=len;i>1;i--){
        Swap(A[1],A[i]);
        HeadAdjust(A,1,i-1);    
        //只需调整以第一个非叶结点为根的树即可，
        //因为上面交换的那一步只是把根节点和最后一个结点交换了
        //处最上层之外其他的子堆都还是满足大根堆的要求的
        //所以只需把最上层出现的小元素不断"下坠"即可
    }
    
}

效率分析

1. 建堆的时间复杂度T1(n) = O(n)
2. 每趟排序的时间复杂度=O(log2n) ; 一共需要排序(n-1)趟，故排序的时间复杂度T2(n) = O(nlog2n)
3. 所以，堆排序总的时间复杂度= T1(n) + T2(n) = O(n) + O(nlog2n) = O(nlog2n) ;
4. 空间复杂度 S(n) = O(1)
5. 算法稳定性：不稳定
6. 基于"大根堆"的堆排序得到递增序列，基于"小根堆"的堆排序得到递减序列
   

拓展

堆是用来排序的数据结构，排序时效率很高，但如果用来查找则是一种效率很低的数据结构，因为查找时堆是无序的，或者说不是严格有序，堆中只是保证了父节点的值一定大于或小于它的两个孩子而已。

8.5 归并排序和基数排序

8.5.1 归并排序(2路归并)

核心操作：把数组内的两个有序序列归并为一个
常用于外部排序

代码实现：

int *B=(int *)malloc(sizeof(int)*n);	//辅助数组B

//A[low…mid]和A[mid+1…high]各自有序，将两个部分合并
void Merge(int A[],int low,int mid,int high){
	int i,j,k;
    for(i=low;i<=high;i++){
        B[i]=A[i];			//将A中所有元素复制到B中
    }
    for(i=low,j=mid+1,k=low;i<=mid&&j<=high;k++){
        if(B[i]<=B[j])
            A[k]=B[i++];		//将较小值复制到A中
        else
            A[k]=B[j++];
    }
    while(i<=mid)
        A[k++]=B[i++];
    while(j<=high)
        A[k++]=B[j++];
}

void MergeSort(int A[],int low,int high){
    if(low<high){
        int mid=(low+high)/2;		//从中间划分
        MergeSort(A,low,mid);		//对左半部分排序
        MergeSort(A,mid+1,high);	//对右半部分排序
        Merge(A,low,mid,high);		//归并左右两个有序序列
    }
} 

效率分析

1. 时间复杂度分析：
   n个元素进行2路归并排序，归并趟数=log2n(向上取整)
   每趟归并时间复杂度为O(n),则算法总的时间复杂度为O(nlog2n)

2. 空间复杂度：O(n) 来自辅助数组B

3. 算法稳定性：稳定
   

8.5.2 基数排序

1. 能手动模拟算法运行过程即可，不考察代码
2. 不需要基于比较的排序
3. 大多基于链式存储结构实现（建立链式队列）
4. 为实现多关键字排序，通常有两种方法：
   1. 最高位优先（MSD） ----按关键字权重递减依次进行分配、收集
   2. 最低位优先（LSD） ----按关键字权重递增依次进行分配、收集
      

擅长解决的问题

①数据元素的关键字可以方便地拆分为d组，且d较小
②每组关键字的取值范围不大，即r很小
③数据元素个数n较大

效率分析

1. 空间复杂度 = O® r是基数，代表每位关键字可以取值的个数，比如十进制数的r=10
2. 一趟分配的时间复杂度=O(n),一趟收集O®,总共d趟分配、收集，总的时间复杂度=O(d(n+r))
3. 算法稳定性：稳定
   

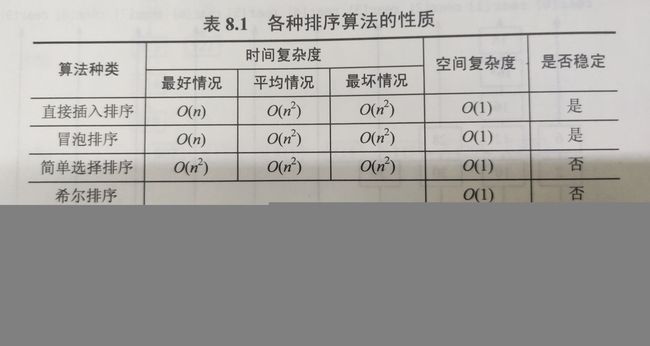
各种排序算法的性质

• 在最好的情况下，时间复杂度可以达到线性时间的有：冒泡排序、直接插入排序。