乘法器
一、乘累加乘法器
对于n比特数，其二进制数转换为有符号十进制数的公式如下：
当B>=0，B的第n-1比特为0，则B可用下式表示：
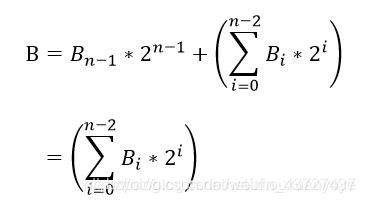
设n=4，“5”的二进制为0101，则5=1 * 4 + 1 * 1
当B<0时，B的第n-1bit为1，B已为补码表示。
所以-|B|表示如下：
综上所述，有符号数与无符号数与十进制的转换表示可统一为如下格式：
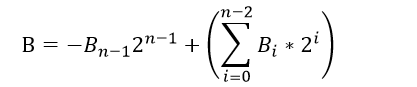
对于正数或0，Bn-1=0；
对于负数，Bn-1=1
对于n比特无符号数：
最小数是： 0
最大数是2^n - 1
对于n比特有符号数：
最小数：-2^(n-1)
最大数：2^(n-1) - 1
从上式可以看出，n比特乘法，输出位宽2n比特，无论有符号数相乘还是无符号数相乘，均不会产生溢出。
乘法竖式计算
A=5，B=12，求A*B的结果：
5的二进制位为（0101），12的二进制位为（1100）
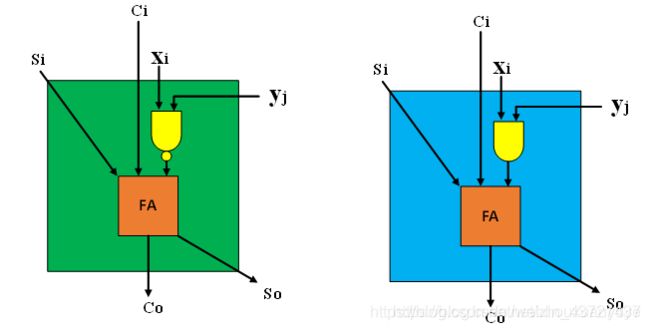
乘累加乘法器
乘法器的本质为加法器的累加和。乘累加乘法器，通过乘–移位–累加的方式，通过多次加法求和的方式计算结果。上述竖式可以看出，B的每一位bit与A相乘后进行移位，最后按列相加，结果表示如下，其中i为比特序号，n为位宽：
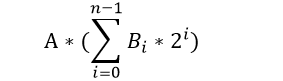
其展开的结构如下：
以上结构使用了n-1个n比特加法器，将耗费大量资源，所以使用如下串行结构的乘法器。
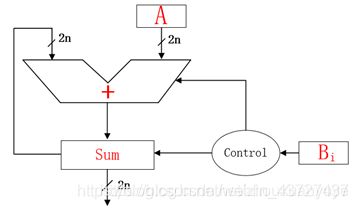
该串行结构乘法器使用一个加法器，由控制逻辑和输入数寄存器A、B组成，此种结构多种多样，基本原理均在于移位加。一个16位乘法器，n=16，乘累加次数为16，由sum作为中间数暂存，Bi作为控制A是否被加入到sum中，且每次A向左移1bit，A *B输出bit位宽32.
串行乘法器时间延迟大，但是面积消耗小。在verilog设计中，直接使用“*”就可以了。
二、阵列乘法器
4bit的AB两数相乘的竖式计算表示成如下，为了区分，方便在阵列格式中看出差异，图中标记了不同的颜色，每组颜色表示一组部分和。
其中aibi表示A和B的某个比特，aibi表示ai与bi相与，使用与门电路生成，aibi的值只有0和1,。S表示AB相乘的结果。
每一列将使用半加器或者全加器两两相加，其结果表示为Si，如S0=a0b0，S1=（a1b0+a0b1）mod2,每一列每两个数产生的进位将传递至相邻高的一列参与计算。
所以，将其结构表示为如下结构，即阵列乘法器（Array Multiplier）。
其中HA表示半加器，FA表示全加器，虚线箭头表示进位传播的路线。使用行波进位加法器RCA搭建如上的阵列乘法器即RCA阵列乘法器。
对于m * n的RCA阵列乘法器，将消耗资源如下：
（1）m * n个与门
（2）n个半加器
（3）mn-m-n个加法器
根据进位传播链，可以看出RCA阵列乘法器的关键路径如下：
上图中红线和紫线是该阵列乘法器中由于累加造成的进位链的最长路径。
通过使用不同结构的加法器可缩短该进位链的传播延时，如使用进位保留加法器（Carry Save Adder，CSA）。
将RCA阵列乘法器的进位链连接至斜下角的加法器，变成上图结构级CSA阵列乘法器，CSA结构的阵列乘法器进位与和分贝金酸，不必计算该层的进位，省去了行波进位加法器进位链的依赖，只在最后一级通过RCA结构（上与绿色框）传递进位合并最后的结果。
将两个结构的阵列乘法器面积与关键路径对比如下：
RCA结构乘法器使用了8个FA、4个·HA，关键路径经过5个FA、2个HA。
CSA结构乘法器使用了8个FA、4个HA，关键路径经过3个FA、3个HA。
CSA结构使用相同的资源却有更优的性能。
根据上例子设计4*4无符号RCA阵列乘法器，主要要点如下：
（1）与门结构，将输入Ai和Bi相与
（2）半加器和全加器，用与求解阵列乘法器的部分和，对于4 * 4阵列乘法器，该部分和个数3个。如果扩展成任意位宽的乘法器，可以使用generate…endgenerate生成每个层级的信号
（3）阵列结构拓扑结构，因为每一部分是行波进位加法器结构，所以，将每个部分和看成N比特的行波进位加法器器，即RCA。
module full_adder(
input a,
input b,
input cin,
output cout,
output s
);
assign s = a^b^sin;
assign cout = a&b | (cin&(a^b));
endmodule
module rca #(width=16)(
input [width-1:0] op1,
input [width-1:0] op2,
outpur [width-1:0] sum,
output cout
);
wire [width:0] temp;
assign temp[0] = 0;
genvar i;
for (i=0;i<width;i=i+1) begin
full_addr full_addr_inst(
.a(op1[i]),
.b(op2[i]),
.cin(temp[i]),
.cout(temp[i+1]),
.s(sum[i])
);
end
assign cout = temp[width];
endmodule
module rca_array_mul#(width=4)(
input [width-1:0] A,
input [width-1:0] B,
output [2*width-1:0] S
);
//for AB and
wire [width-1:0] [width-1:0] ab;
//rca inputs
wire [width-1:0] leve10_op1;
wire [width-1:0] leve10_op2;
wire [width-1:0] leve11_op1;
wire [width-1:0] leve11_op2;
wire [width-1:0] leve12_op1;
wire [width-1:0] leve12_op2;
//rca outputs
wire [width-1:0] leve10_sum;
wire leve10_cout;
wire [width-1:0] leve11_sum;
wire leve11_cout;
wire [width-1:0] leve12_sum;
wire leve12_cout;
//A and B "and gates"
genvar i,j;
generate
for(i=0;i<width;i=i+1) begin
for(j=0;j<width;j=j+1) begin
assign ab[i][j] = B[i] & A[j]
end
end
endgenerate
//leve10 rca
assign leve10_op1 = (1'b0,ab[0][width-1:1]);
assign leve10_op2 = ab[1][width-1:0];
rca #(4) rca_inst(
.op1(leve10_op1),
.op2(leve10_op2),
.sum(leve10_sum),
.cout(leve10_cout)
);
//leve11 rca
assign leve11_op1 = (leve10_cout,leve10_sum[width-1:1]);
assign leve11_op2 = ab[2][width-1:0];
rca #(4) rca_inst(
.op1(leve11_op1),
.op2(leve11_op2),
.sum(leve11_sum),
.cout(leve11_cout)
);
//leve12 rca
assign leve12_op1 = (leve11_cout,leve11_sum[width-1:1]);
assign leve12_op2 = ab[3][width-1:0];
rca #(4) rca_inst(
.op1(leve12_op1),
.op2(leve12_op2),
.sum(leve12_sum),
.cout(leve12_cout)
);
//result output
assign S[0] = ab[0][0];
assign S[1] = leve10_sum[0];
assign S[2] = leve11_sum[0];
assign S[2*width-1:3] = {leve12_cout,leve12_sum};
endmodule
三、Baugh-Wooley乘法器
该算法是二进制补码并行阵列相乘算法。该算法转换为等效并行阵列相加，其中每个部分和为乘数和被乘数比特相与，并且所有的部分和符号位为“+”。将n比特X,Y，乘法结构2n比特的P表示如下：
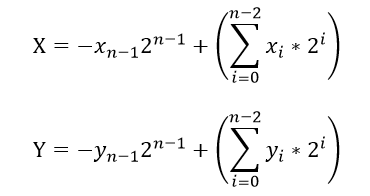
从上式可以看出，XY相乘，结果P=XY相当于前两项减去后两项正数，设为A和B.
按顺序用字母表示以上项，即P=C+D-(A+B)
将最后两项A和B，补0扩展表示成2n位，以便在阵列中相加：
其中ai=y(n-1)*xi。
A的二进制表示如下：
-A，即A的二进制补码，对A取反加1，表示如下：
取反：
加一：
B的补码和A同理。
所以，-（A+B）的结果如下，即-A-B：
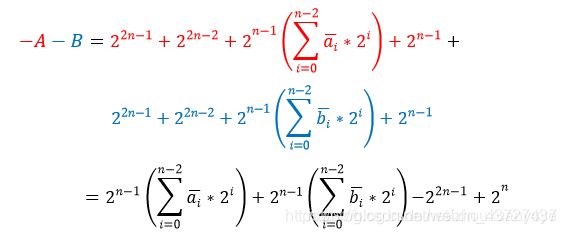
将-A-B带入P的表达式，所以P的结果如下：
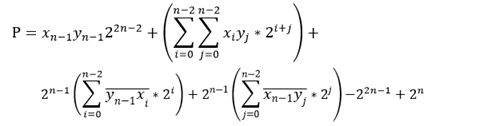
以n=4bit为X、Y相乘为例，P=XY为8bit：
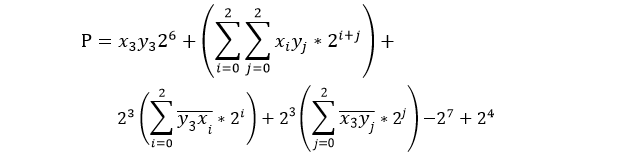该4*4乘法器结构如下：
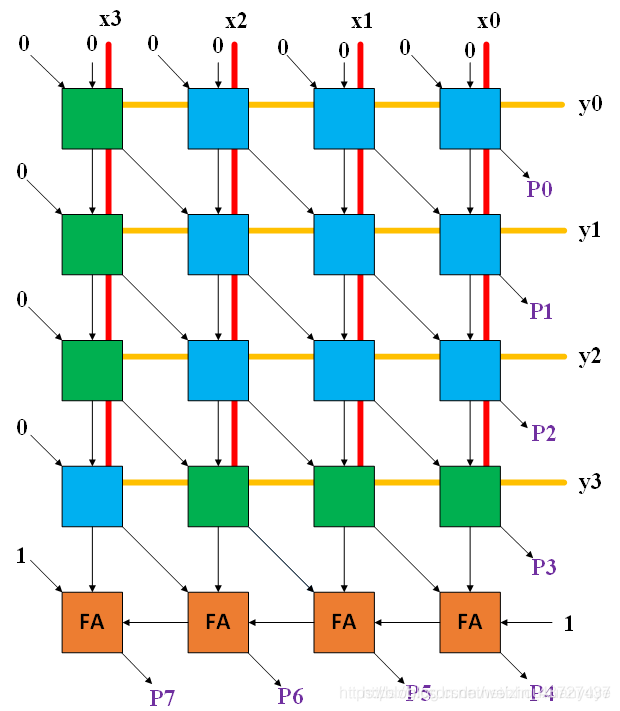以上结果中每个框均为全加器，有微小差距。
蓝色框，其中某个输入xiyi相与；
绿色框，其中某个输入为xiyi相与后取反。
右下斜对角为P的传播路径，上下为进位传播路径，最长的进位链传播为P0的进位至P7的进位传播。
四、图解Wallace树乘法器
Assuming that all summands are generated simultaneously the best possible first step is to group the summands into threes, and introduce each group into its own pseudoadder, thus reducing the count of numbers by a factor of 1.5 ( or a little less, if the number of summands is not multiple of three). The best possible second step is to group the numbers resulting from the first step into threes and again add each group in its own pseudoadder. By continuing such steps until only two numbers remain, the addition is completed in a time proportional to the logarithm of the number of summands.
————————————————
简单讲就是许多个数求和，每3个数分为一组，压缩至2个加数，循环往复。
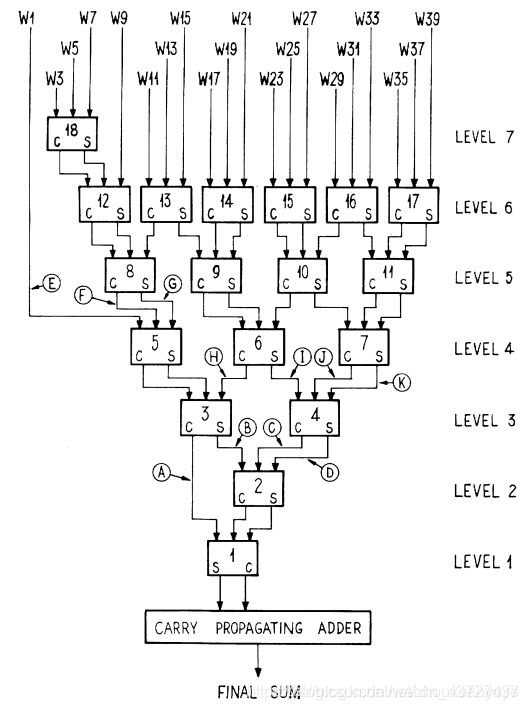
在乘法器中，乘法的积为许多个部分和之和。Wallace结构可以加快乘法器的计算速度。
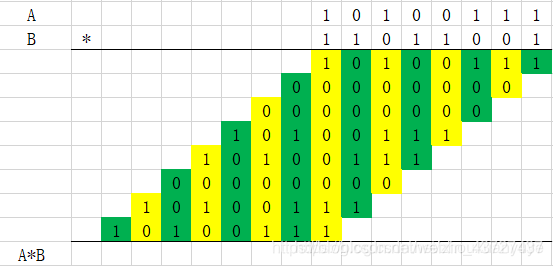
AB两数相乘，按照一般的阵列乘法器，上图中黄色和绿色每一列的加法进位输入依赖前一列的进位输出，而Wallace结构将部分和分组，并同时计算，在最后一级使用加法器传播进位。
以下是8*8bit的阵列乘法器Wallace树结构例子。
（1）、每三个加数一组，分组，不足3个保持。
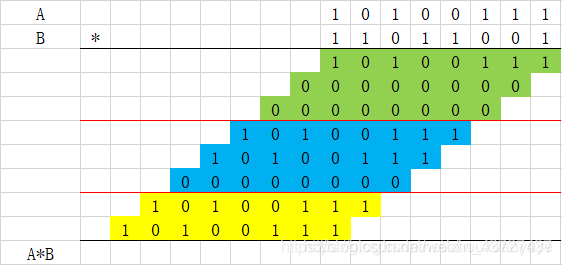
（2）求出以上3个数的和与进位，参考进位保存加法器。
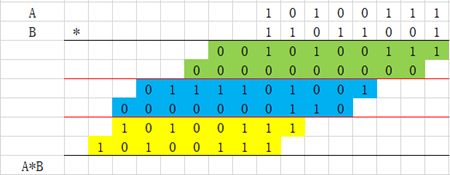
（3）继续每3个加数分组。
（4）求出以上3个数的和与进位。
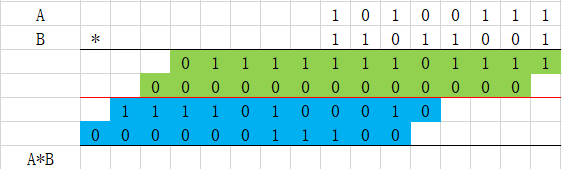
（5）分组
（6）求和与进位
（7）分组
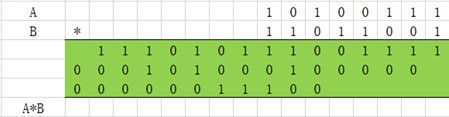
（8）求和与进位
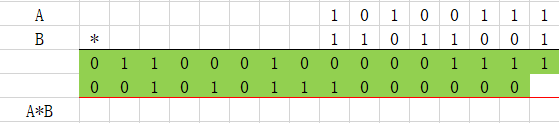
（9）最终结果求和，进位传播加法器
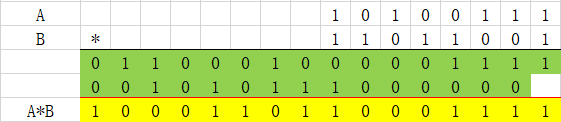
验证：
8’b10100111=167
8’b11011001=217
16’b1000110110001111=36239
module full_adder(
input a,
input b,
input cin,
output cout,
output s
);
assign s = a^b^cin;
assign cout = a&b|(cin&(a^b));
endmodule
module cas#(width=16)(
input [width-1:0] op1,
input [width-1:0] op2,
input [width-1:0] op3,
output [width-1:0] s,
output [width-1:0] c
);
genvar i;
generate
for(i=0;i<width;i=i+1) begin
full_addr full_addr_inst(
.a(op1[i]),
.b(op2[i]),
.cin(op3[i]),
.cout(c[i]),
.s(s[i])
);
end
endgenerate
endmodule
module rca #(width=16)(
input [width-1:0] op1,
input [width-1:0] op2,
input cin,
output cout,
output [width-1:0] sum
);
wire [width:0] temp;
assign temp[0] = cin;
assign cout = temp[width];
genvar i;
for(i=0;i<width;i=i+1) begin
full_adder u1(
.a(op1[i]),
.b(op2[i]),
.cin(temp[i])，
.cout(temp[i+1]),
.s(sum[i])
);
end
endmodule
module wallace_mul #(width=8)(
input [width-1:0] x,
input [width-1:0] y,
output [2*width-1:0] p
);
wire [width-1:0][2*width-1:0] xy;
wire [width*2-1:0] s_lev01;
wire [width*2-1:0] c_lev01;
wire [width*2-1:0] s_lev02;
wire [width*2-1:0] c_lev02;
wire [width*2-1:0] s_lev11;
wire [width*2-1:0] c_lev11;
wire [width*2-1:0] s_lev12;
wire [width*2-1:0] c_lev12;
wire [width*2-1:0] s_lev21;
wire [width*2-1:0] c_lev21;
wire [width*2-1:0] s_lev31;
wire [width*2-1:0] c_lev31;
genvar i;
genvar j;
generate
for(i=0;i<width;i=i+1) begin
for(j=0;j<width;j=j+1) begin
assign xy[i][j] = y[i]&x[i];
end
assign xy[i][2*width-1:width] = 8'd0;
end
endgenerate
//level 0
csa #(width*2) csa_lev01(
.op1(xy[0]),
.op2(xy[1]<<1),
.op3(xy[2]<<2),
.s(s_lev01),
.c(c_lev01)
);
csa #(width*2) csa_lev02(
.op1(xy[3]<<3),
.op2(xy[4]<<4),
.op3(xy[5]<<5),
.s(s_lev02),
.c(c_lev02)
);
//level 1
csa #(width*2) csa_lev11(
.op1(s_lev01),
.op2(c_lev01<<1),
.op3(s_lev02),
.s(s_lev11),
.c(c_lev11)
);
csa #(width*2) csa_lev12(
.op1(s_lev01<<1),
.op2(c_lev01<<6),
.op3(s_lev02<<7),
.s(s_lev12),
.c(c_lev12)
);
//level 2
csa #(width*2) csa_lev21(
.op1(s_lev11),
.op2(c_lev11<<1),
.op3(s_lev12),
.s(s_lev21),
.c(c_lev21)
);
//leve1 3
csa #(width*2) csa_lev31(
.op1(s_lev21),
.op2(c_lev21<<1),
.op3(c_lev12<<1),
.s(s_lev31),
.c(c_lev31)
);
//adder
rca #(2*width) u_rca(
.op1(s_lev31),
.op2(c_lev31<<1),
.cin(1'b0),
.sum(p),
.cout()
);
endmodule
五、Radix-2 Booth乘法器
布斯乘法算法（Booth‘s multiplication algorithm)是计算机中一种利用二进制的补码形式来计算乘法的算法。相对于传统的乘法器速度更快，面积更小。
Booth算法描述
布斯算法的实现可以通过重复地在P上加两个预设值A和S其中的一个，然后对P实施算术右移。设m和r分别为被乘数和乘数，再令x和y分别为m和r中的数字位数。
第一步： 确定A和S的值，以及P的初始值。这个三个数字的长度都应等于（x+y+1）：
对于A：以m的值填充到前x位（最靠左的位），用零填满剩下的（y+1）位；
对于S：以（-m）的值填充到前x位，用零填满剩下的（y+1）位；
对于P：用0填满最左的x位，将r的值附加在尾部；最右一位用零占位（辅助位，当i=0时，i-1=-1指的就是这个辅助位）；
第二步： 观察P的最右两位：
如果等于01，求出P+A的值，忽略上溢；
如果等于10，求出P+S的值，忽略上溢；
如果等于00，不做任何运算，在下一步中直接采用P的值；
如果等于11，不做任何运算，在下一步中直接采用P的值；
第三步： 对第二步中得到的值进行算术右移一位，并将结果赋给P；
第四步： 重复第二步和第三步，一共做y次；
第五步： 舍掉P的最后一位，得到的即为m和r的积。
Booth的原理
考虑一个由若干个0包围着若干个1的正的二进制乘数，比如00111110，积可以表达为：
M x 00111110 = M x (2 ^ 5 + 2 ^ 4 + 2 ^ 3 + 2 ^ 2 + 2 ^ 1) = M x 62
其中，M代表被乘数。变形为以下可以使运算次数可以减少为两次：
M x 010000(-1)0 = M x (2 ^ 6 - 2 ^ 1)= M x 62
事实上，任何二进制数中连续的1可以被分解为两个二进制数之差：
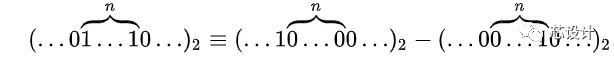
因此，我们可以用更简单的运算来替原数中连续为1的数字的乘法，通过加上乘数，对部分积进行移位运算，最后再将之从乘数中减去。利用了我们在针对为零的位做乘法时，不需要做其他运算，只需要移位这一特点，这就像我们在做和99的乘法时，利用99=100-1这一性质，这种模式可以扩展应用于任何一串数字中连续为1的部分（包括只有一个1的情况），那么：
M x 00111010 = M x (2 ^ 5 + 2 ^ 4 + 2 ^ 3 + 2 ^ 1) = M x 58
M x 0100(-1)010 = M x (2 ^ 6 - 2 ^ 3 + 2 ^ 1) = M x 58
布斯算法遵从这种模式，在遇到一串数字中的第一组从0到1的变化时（即遇到01）时，执行加法，在一连串连续1的尾部时（即遇到10时）执行减法，这在乘数为负时同样有效。当乘数中的连续1比较多时，布斯算法较一般的乘法算法执行的加减法运算更少。
下图是4*4的booth乘法器，被乘数和乘数分别为：7和-3.结果-21.
Booth算法的流程图如下，其中M为被乘数，Q为乘数，N为M和Q的bM的it位数，A为与M位宽相等的寄存器：
这里的算法流程和上述的扩位宽的其实是一样的。
module booth #(parameter WIDTH=4)(
input clk,
input enable,
input [WIDTH-1:0] multiplier,
input [WIDTH-1:0] multiplicand,
output reg done,
output reg [2*WIDTH-1:0] product
);
parameter IDLE = 2'b00, ADD = 2'b01, SHIFT = 2'b10, OUTPUT = 2'b11;
reg [1:0]c_state,n_state;
reg [2*WIDTH+1:0] a_reg,s_reg,p_reg,sum_reg;
reg [WIDTH-1:0] iter_cnt;
reg [WIDTH:0] multiplier_neg;
always @ (posedge clk) begin
if(!enable) begin
c_state <= IDLE;
end
else begin
c_state <= n_state;
end
end
always @ (*) begin
case(c_state)
IDLE : if(enable) n_state = ADD;
else n_state = IDLE;
ADD : n_state = SHIFT;
SHIFT : if(iter_cnt==WIDTH) n_state = OUTPUT;
else n_state = ADD;
OUTPUT : n_state = IDLE;
default : n_state = IDLE;
endcase
end
assign multiplier_neg = -{multiplier[WIDTH-1],multiplier};
always @ (posedge clk) begin
case(c_state)
IDLE : begin
a_reg <= {multiplier[WIDTH-1],multiplier,{(WIDTH+1){1'b0}}};
s_reg <= {multiplier_neg,{(WIDTH+1){1'b0}}};
p_reg <= {{(WIDTH+1){1'b0}},multiplicand,1'b0};
iter_cnt <= 0;
done <= 1'b0;
end
ADD : begin
case(p_pre[1:0])
2'b01 : sum_reg <= p_reg + a_reg;
2'b10 : sum_reg <= p_reg + s_reg;
2'b00,2'b11 : sum_reg <= p_reg;
endcase
iter_cnt <= iter_cnt + 1'b1;
end
SHIFT : begin
p_pre <= {sum_reg[2*WIDTH+1],sum_reg[2*WIDTH+1]:1};
end
OUTPUT : begin
product <= p_pre[2*WIDTH:1];
done <= 1'b1;
end
endcase
end
endmodule
因为在实际中基2 Booth算法使用较少。
六、 Radix-4 Booth乘法器原理
对于N比特数B来说：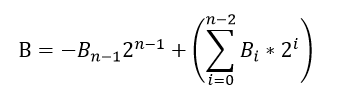
N比特数B，将其展开，其中B-1=0：
基2 Booth表示为：
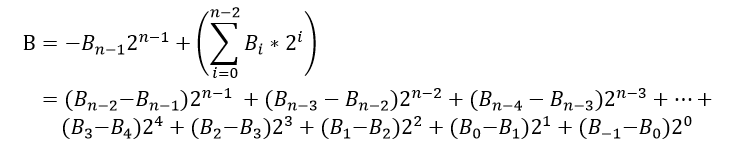其基系数为：
基4 Booth乘法器的基系数为：
所以上式B可以重写为如下式（位宽为偶数）：
将A与B相乘，则：
以下是基4 Booth编码表，其中A为被乘数，B为乘数
以下是6比特数9的Radix-2 Booth和Radix-4 Booth编码例子：
从基2看9：
9 = 0 * 2 ^ 5 + 1 * 2 ^ 4 + (-1) * 2 ^ 3 + 0 * 2 ^ 2 + 1 * 2 ^ 1 + (-1) * 2 ^ 0
从基4看9：
9 = 1 * 4 ^ 2 + (-2) * 4 ^ 1 + 1 * 4 ^ 0
其阵列表达式如下：
可以看出，6比特乘数的基2 Booth算法部分累积和个数为6，而基4的部分累积和数为3.
相比于基2 Booth编码，基4 Booth编码将使得乘法累积部分和数减少一半，其基系数只涉及到移位和补码计算。对于二进制补码为1010…1010的乘数（1和0交替），如果采用基2 Booth编码，则部分和累积的输入有几乎一半为被乘数的补码没，所以相当于普通的阵列乘法器，基2 Booth编码乘法器性能不升反降，基4 Booth编码可以避免以上问题。