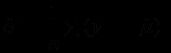Box-Cox变换
1 Box-Cox变换
在回归模型号中,Box-Cox变换是对因变量Y作如下变换:
这里![]() 是一个待定变换参数。对不同的
是一个待定变换参数。对不同的![]() ,所做的变换自然就不同,所以是一个变换族。它包括了对数变换(
,所做的变换自然就不同,所以是一个变换族。它包括了对数变换(![]() =0),平方根变换(
=0),平方根变换(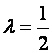 )和倒数变换(
)和倒数变换(![]() =-1)等常用变换。
=-1)等常用变换。
图1. 变换前变量的分布
图2.变换后变量分布
也就是说,通过对因变量的变换,使得变换过的向量![]() 与回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。
与回归自变量具有线性相依关系,误差也服从正态分布,误差各分量是等方差且相互独立。
当![]() 固定时,
固定时,![]() 是不依赖于参数
是不依赖于参数![]() 和
和![]() 的常数因子。
的常数因子。![]() 的其余部分关于
的其余部分关于![]() 和
和![]() 求导数,令其等于0,可以求得
求导数,令其等于0,可以求得![]() 和
和![]() 的极大似然估计
的极大似然估计
为了求![]() 的最大值,考虑到lnx是x的单调函数,对
的最大值,考虑到lnx是x的单调函数,对![]() 求对数。略去与
求对数。略去与![]() 无关的常数项,得到
无关的常数项,得到
其中
(1.9)式对Box-Cox变换带来很大方便,因为为了求![]() 的最大值,只需求残差平方和的
的最大值,只需求残差平方和的![]() 最小值。
最小值。
2 单变量的Box-Cox变换
对极大似然函数作对数变换
化简得
其中
(2.9)亦即为几何平均值。
为了简单起见,重新将Box-Cox变换定义为
3 黄金分割搜索法
黄金分割法(Golden Section Method),是用于在单峰函数区间上求极小值的一种方法。其基本思想是通过取试探点和函数值比较,使包含极小点的搜索区间不断减少,当区间长度缩短到一定程度时,就得到函数极小点的近似值。
对于函数![]() ,先在搜索区间[a,b]上确定两个试探点,其中左试探点为
,先在搜索区间[a,b]上确定两个试探点,其中左试探点为
右试探点为
再分别计算这两个试探点的函数值![]() ,
,![]() 。由单峰函数的性质,若
。由单峰函数的性质,若![]() ,则区间
,则区间![]() 内不可能有极小点,因此去掉区间
内不可能有极小点,因此去掉区间![]() ,令a’=a,b’=
,令a’=a,b’=![]() ,得到一个新的搜索区间。若
,得到一个新的搜索区间。若![]() ,则区间
,则区间![]() 内不可能有极小点,去掉区间
内不可能有极小点,去掉区间![]() ,令a’=
,令a’=![]() ,b’=b,得到一个新的搜索区间。
,b’=b,得到一个新的搜索区间。
类似上面的步骤,在区间[a’,b’]内再计算两个新的试探点
比较函数值,得到新的区间。
在上述方中,事实上每次迭代并不需要计算两个试探点及函数值。下面对新的试探点进行分析。
即原区间的左试探点。
即原区间的右试探点。
因此在上述计算过程中,只需要计算一个新试探点和一个点的函数值。
算法:
(1) 置初始搜索区间[a,b],并置精度要求![]() ,并计算左右试探点
,并计算左右试探点
并计算
否则
并计算
(3) 若|b-a|![]() ,如果
,如果![]() ,则置问题的解
,则置问题的解![]() ;否则置
;否则置![]() ,停止计算。否解转到(2)继续计算。
,停止计算。否解转到(2)继续计算。
4 正态分布检验
I. W检验
W检验是S.S.Shapiro和M.B.Wilk1965年提出来的,这种方法在样本容量3![]() n
n![]() 50时适用。
50时适用。
W检验即检验假设
(1) 把n个样本观测值按由小到大的次序排列成
(2) W检验的统计量为
(3) 根据给定的检验水平![]() 和样本容量n查表得统计量W的
和样本容量n查表得统计量W的![]() 的分位数
的分位数![]() 。
。
(4) 作出间判断:若W<![]() ,则拒绝
,则拒绝![]() ,认为总体不服从正态分布;若W
,认为总体不服从正态分布;若W![]()
![]() ,则不拒绝
,则不拒绝![]() 。
。
II. D检验
W检验是一种有效的正态性检验方法,可惜它只适用于容量为3至50的样本。1971年D’Agostino提出了D’Agostino检验(简称D检验)。这种检验不需要附系数表,它所适用的样本容量n的范围为50![]() n
n![]() 1000。
1000。
进行D检验的步骤如下:
(1) 把n个样本观测值按由小到大的次序排列成
(2) D检验的统计量为
其中
按(4.2)和(4.3)式计算统计量Y的值。
(3) 根据给定的检验水平![]() 和样本容量n查表,得统计量Y的
和样本容量n查表,得统计量Y的![]() 分位数
分位数![]() 和1-
和1-![]() 分位数
分位数![]() ;
;
附:Box-Cox变换的R代码
BoxCox_Trans<-function(x,interval,loop=1000,epsilon= .Machine$double.eps){
Likelihood_Log<-function(x,lambda){
y_lambda<-function(x,lambda){
gm<-exp(mean(log(x)))
if (lambda == 0)
log(x) * gm
else (gm^(1 - lambda)) * ((x^lambda) - 1)/lambda
}
y <- y_lambda(x, lambda)
(length(y)/2) * log(((length(y) - 1)/length(y)) * var(y))
}
GoldenSecSearch<-function(f,x,interval,loop, epsilon)
{
t<-(sqrt(5) - 1)/2
a<-min(interval)
b<-max(interval)
a_l<-a+(1-t)*(b-a)
a_r<-a+t*(b-a)
f_l<-f(x,a_l)
f_r<-f(x,a_r)
i<-1
while(abs(b-a)>epsilon){
i<-i+1
if(f_l<f_r){
b<-a_r
a_r<-a_l
f_r<-f_l
a_l<-a+(1-t)*(b-a)
f_l<-f(x,a_l)
}
else {
a<-a_l
a_l<-a_r
f_l<-f_r
a_r<-a+t*(b-a)
f_r<-f(x,a_r)
}
if(i>loop) break
}
Result<-list()
if(f_l<f_r) {
Result$minimum<-a_l
Result$Objective<-f_l
}
else {
Result$minimum<-a_r
Result$Objective<-f_r
}
Result
}
Output<-list()
Output<- GoldenSecSearch(Likelihood_Log,x,interval,loop,epsilon)
Output
}
进行变换的R代码
> attach(Prestige) //car package
> hist(income)
> BoxCox_Trans(income,seq(-3,3))
$minimum
[1] 0.1792894
$Objective
[1] 827.9459
> hist(income^0.1792894)