【数据结构-二叉树】递归框架&数据结构搜索基础入门
【数据结构-二叉树】框架以及数据结构搜索基础入门
结合1.框架 + 2.第三章数据机构基础的搜索。
1. 引言
前文的回溯、动规、分治算法,其实都是树的问题,而树的问题就永远逃不开树的递归遍历框架这几行代码:
/* 二叉树遍历框架 */
void traverse(TreeNode root) {
// 前序遍历
traverse(root.left)
// 中序遍历
traverse(root.right)
// 后序遍历
}
**【注意】**上述代码看起来“破” “简单”;但是 —— 实际如何写递归/递归的运用、二叉树的本质 – 在树节点处学要做什么 、即:需要递归返回什么 & 形参需要传递什么… 等都是需要通过多刷题和总结的学问。
举个例子,比如说我们的经典算法「快速排序」和「归并排序」,对于这两个算法,你有什么理解?如果你告诉我, 快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后续遍历,那么我就知道你是个算法高手了。
为什么快速排序和归并排序能和二叉树扯上关系?我们来简单分析一下他们的算法思想和代码框架:
快速排序的逻辑是,若要对nums[lo…hi]进行排序,我们先找一个分界点p,通过交换元素使得nums[lo…p-1]都小于等于nums[p],且nums[p+1…hi]都大于nums[p],然后递归地去nums[lo…p-1]和nums[p+1…hi]中寻找新的分界点,最后整个数组就被排序了。
快速排序的代码框架如下:
void sort(int[] nums, int lo, int hi) {
/****** 前序遍历位置 ******/
// 通过交换元素构建分界点 p
int p = partition(nums, lo, hi);
/************************/
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}
先构造分界点,然后去左右子数组构造分界点,你看这不就是一个二叉树的前序遍历吗?
再说说归并排序的逻辑,若要对nums[lo…hi]进行排序,我们先对nums[lo…mid]排序,再对nums[mid+1…hi]排序,最后把这两个有序的子数组合并,整个数组就排好序了。
归并排序的代码框架如下:
void sort(int[] nums, int lo, int hi) {
int mid = (lo + hi) / 2;
sort(nums, lo, mid);
sort(nums, mid + 1, hi);
/****** 后序遍历位置 ******/
// 合并两个排好序的子数组
merge(nums, lo, mid, hi);
/************************/
}
先对左右子数组排序,然后合并(类似合并有序链表的逻辑),你看这是不是二叉树的后序遍历框架?另外,这不就是传说中的分治算法嘛,不过如此呀。
如果你一眼就识破这些排序算法的底细,还需要背这些算法代码吗?这不是手到擒来,从框架慢慢扩展就能写出算法了。
2. 写递归算法的秘诀
【重点:】写递归算法的关键是要明确函数的「定义」是什么,然后相信这个定义,利用这个定义推导最终结果,绝不要试图跳入递归。
怎么理解呢,我们用一个具体的例子来说,比如说让你计算一棵二叉树共有几个节点:
// 定义:count(root) 返回以 root 为根的树有多少节点
int count(TreeNode root) {
// base case
if (root == null) return 0;
// 自己加上子树的节点数就是整棵树的节点数
return 1 + count(root.left) + count(root.right);
}
这个问题非常简单,大家应该都会写这段代码,root本身就是一个节点,加上左右子树的节点数就是以root为根的树的节点总数。
左右子树的节点数怎么算?其实就是计算根为root.left和root.right两棵树的节点数呗,按照定义,递归调用count函数即可算出来。
写树相关的算法,简单说就是,先搞清楚当前root节点该做什么,然后根据函数定义递归调用子节点,递归调用会让孩子节点做相同的事情。
【注意以下重点:】
①说了这么多,旨在说明,二叉树的算法思想的运用广泛,甚至可以说,只要涉及递归,都可以抽象成二叉树的问题。【注意:不要僵固的认为——递归的结点代表数组一个数!不一定 —— 比如之前的回溯搜索树对应的是多个数组 —— 所以二叉树递归的节点 表明的是一种状态[即:当前位置的 所态所做]。】
②写递归算法的关键是要明确函数的「定义」是什么,然后相信这个定义,利用这个定义推导最终结果,绝不要试图跳入递归。
所以接下来,我们直接上几道比较有意思,且能体现出递归算法精妙的二叉树题目,手把手教你怎么用算法框架搞定它们。
二叉树题目的一个难点就是,如何把题目的要求细化成每个节点需要做的事情。
③ 做二叉树的问题,关键是把题目的要求细化,搞清楚根节点应该做什么,然后剩下的事情抛给前/中/后序的遍历框架就行了。
3. 二叉树题目
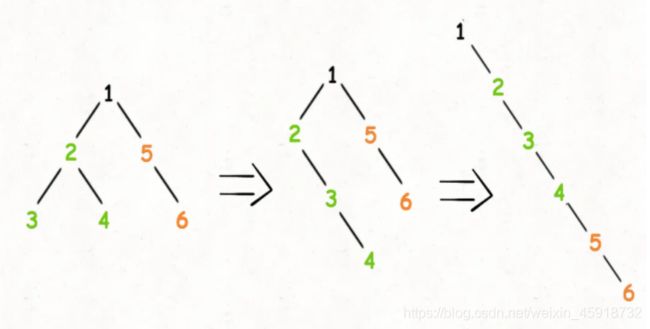
3.1 二叉树展开为链表
给flatten函数输入一个节点root,那么以root为根的二叉树就会被拉平为一条链表。
我们再梳理一下,如何按题目要求把一棵树拉平成一条链表?很简单,以下流程:
1、将root的左子树和右子树拉平。
2、将root的右子树接到左子树下方,然后将整个左子树作为右子树。
上面三步看起来最难的应该是第一步对吧,如何把root的左右子树拉平?其实很简单,按照flatten函数的定义,对root的左右子树递归调用flatten函数即可:
我的题解:
/**
* @Description: 递归 且 重想不干扰原先结构。
* @param {TreeNode} *root
* @return {*}
* @notes: 【可以后序遍历】
*/
void flatten(TreeNode *root)
{
if(root == nullptr) return ;
flatten(root->left);
flatten(root->right);
// 开始展开成一侧 并 重置为nullptr
if(root->left == nullptr) return;
// 两侧都有值,开始 flatten
TreeNode* tmp = root->right;
root->right = root->left;
// 寻找最后一个 尾节点链接到tmp
TreeNode* cur=root->right;
while(cur->right != nullptr) cur = cur->right;
cur->right = tmp;
root->left = nullptr;
}
你看,这就是递归的魅力,你说flatten函数是怎么把左右子树拉平的?不容易说清楚,但是只要知道flatten的定义如此,相信这个定义,让root做它该做的事情,然后flatten函数就会按照定义工作。
另外注意递归框架是后序遍历,因为我们要先拉平左右子树才能进行后续操作。
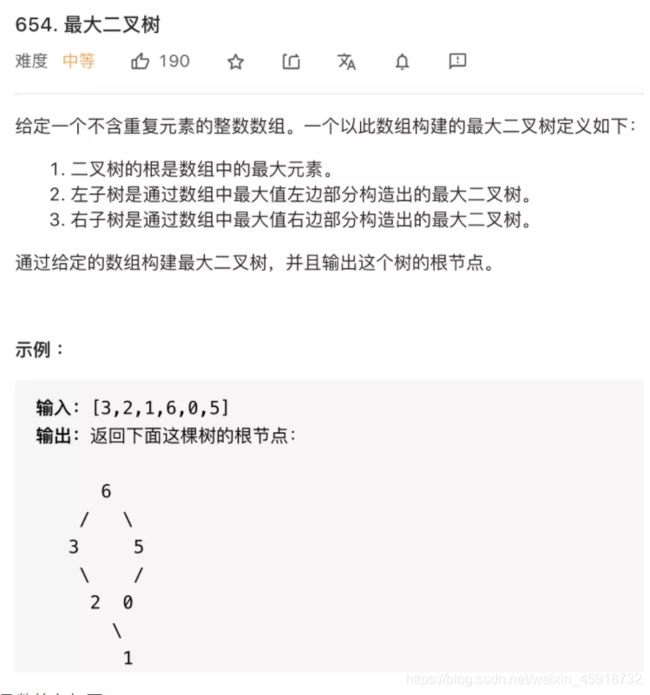
3.2 最大二叉树-简单TreeNode*初始化递归
题解思路:
按照我们刚才说的,**先明确根节点做什么?**对于构造二叉树的问题,根节点要做的就是把想办法把自己构造出来。
我们肯定要遍历数组把找到最大值maxVal,把根节点root做出来,然后对maxVal左边的数组和右边的数组进行递归调用,作为root的左右子树。
对于每个根节点,只需要找到当前nums中的最大值和对应的索引,然后递归调用左右数组构造左右子树即可。
我的解法:
class Solution
{
public:
TreeNode *constructMaximumBinaryTree(vector<int> &nums)
{
if (nums.empty())
return nullptr;
// 寻找最大节点
// unordered_set list(nums.begin(), nums.end());
int point = max_element(nums.begin(), nums.end()) - nums.begin(); // 对应的下标,因为返回的是it 迭代器
cout << "Now point is : " << point;
cout << ";Now pointnum is : " << nums[point] << endl;
TreeNode* root = new TreeNode(nums[point]); // 默认为 null了
// 边界
if (point > 0)
{
vector<int> nums1(nums.begin(), nums.begin() + point);
root->left = constructMaximumBinaryTree(nums1); // 左边部分的递归
}
if (point < nums.size() - 1)
{
vector<int> nums2(nums.begin() + point + 1, nums.end());
root->right = constructMaximumBinaryTree(nums2); // 左边部分的递归
}
return root;
}
};
注意:类和结构体(指针对象)的初始化:【 TreeNode* root = new TreeNode(nums[point]); // 默认为 null了】
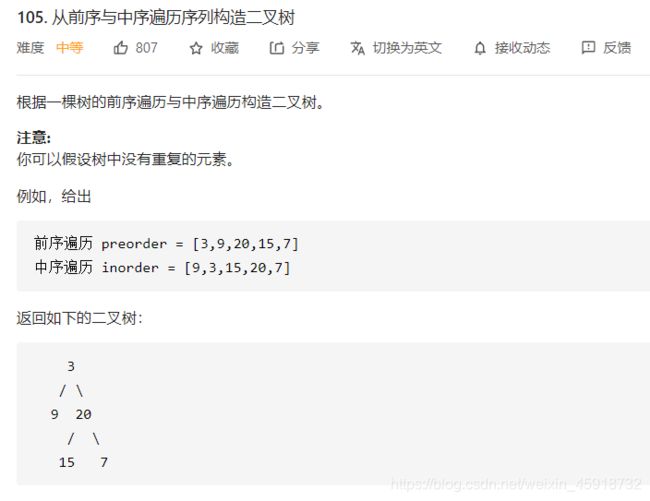
3.3 105.通过前序和中序遍历结果构造二叉树
详见:本节
4.4 部分。
3.4 106.通过后序和中序遍历结果构造二叉树
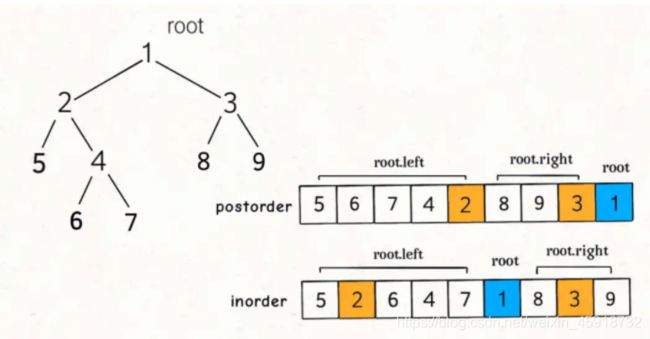
这样的遍历顺序差异,导致了preorder和inorder数组中的元素分布有如下特点:
这道题和上一题的关键区别是,后序遍历和前序遍历相反,根节点对应的值为postorder的最后一个元素。
整体的算法框架和上一题非常类似,我们依然写一个辅助函数build:
TreeNode buildTree(int[] inorder, int[] postorder) {
return build(inorder, 0, inorder.length - 1,
postorder, 0, postorder.length - 1);
}
TreeNode build(int[] inorder, int inStart, int inEnd,
int[] postorder, int postStart, int postEnd) {
// root 节点对应的值就是后序遍历数组的最后一个元素
int rootVal = postorder[postEnd];
// rootVal 在中序遍历数组中的索引
int index = 0;
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == rootVal) {
index = i;
break;
}
}
TreeNode root = new TreeNode(rootVal);
// 递归构造左右子树
root.left = build(preorder, ?, ?,
inorder, ?, ?);
root.right = build(preorder, ?, ?,
inorder, ?, ?);
return root;
}
现在postoder和inorder对应的状态如下:
我们可以按照上图将问号处的索引正确填入:
int leftSize = index - inStart;
root.left = build(inorder, inStart, index - 1,
postorder, postStart, postStart + leftSize - 1);
root.right = build(inorder, index + 1, inEnd,
postorder, postStart + leftSize, postEnd - 1);
// or 我的解法对应部分:// 两者一样的!
root->left = helper( postorder, inorderMap, postLeft, postLeft+(pivot-inLeft)-1, inLeft, pivot-1);
root->right = helper( postorder, inorderMap, postLeft+(pivot - inLeft), postLeft+inRight-inLeft-1, pivot+1, inRight); // 【在 倒数第三个 忘了-1】或者 postRight-1 也可以。
有了前一题的铺垫,这道题很快就解决了,无非就是rootVal变成了最后一个元素,再改改递归函数的参数而已,只要明白二叉树的特性,也不难写出来。
我的解法:
class Solution {
public:
/**
* @Description: 使用后序和中序 遍历构建一棵二叉树 —— 类似于前序和中序的反过程
* @param {*}
* @return {*}
* @notes:
*/
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
unordered_map<int,int> inorderMap;
for(int i = 0; i<inorder.size() ;i++){
inorderMap.insert({inorder[i], i});
}
return helper(postorder, inorderMap, 0, postorder.size()-1, 0, inorder.size()-1);
}
// 辅助函数构建二叉树
// 左闭右闭
TreeNode* helper(vector<int> &postorder, unordered_map<int,int> &inorderMap, int postLeft, int postRight, int inLeft, int inRight){
if(postLeft > postRight) return nullptr;
// 相信并想象如何递归构建
TreeNode* root = new TreeNode(postorder[postRight]);
int pivot = inorderMap[postorder[postRight]]; // 寻找 中序的分治点。
// int num_left = pivot - inLeft, num_right = inRight - pivot;
root->left = helper( postorder, inorderMap, postLeft, postLeft+(pivot-inLeft)-1, inLeft, pivot-1);
root->right = helper( postorder, inorderMap, postLeft+(pivot - inLeft), postLeft+inRight-inLeft-1, pivot+1, inRight); // 【在 倒数第三个 忘了-1】或者 postRight-1 也可以。
return root;
}
};
3.5 [拆解题解]递归输出重复子树
还是那句话,根据题意,思考一个二叉树当前节点需要做什么,到底用什么遍历顺序就清楚了。
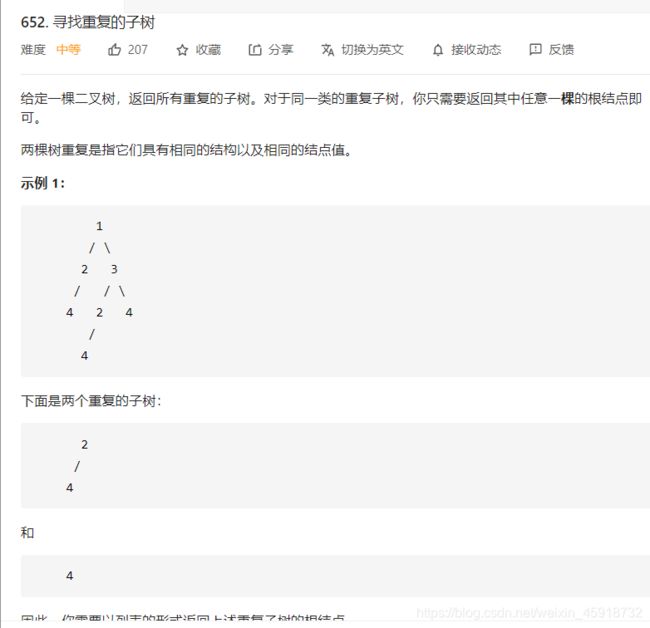
这题咋做呢?还是老套路,先思考,对于某一个节点,它应该做什么。
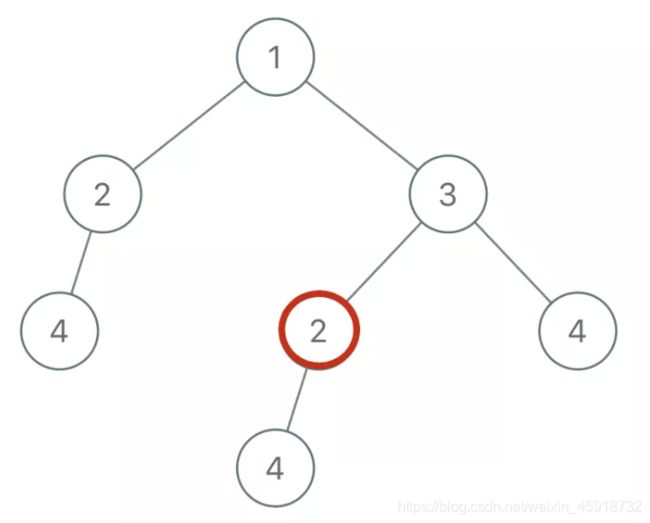
比如说,你站在图中这个节点 2 上:
如果你想知道以自己为根的子树是不是重复的,是否应该被加入结果列表中,你需要知道什么信息?
你需要知道以下两点:
1、以我为根的这棵二叉树(子树)长啥样? [使用 序列化的后序遍历]
2、以其他节点为根的子树都长啥样?[保存 一旦重复则可以输出]
3、要防止重复,因为只是第一次重复的时候输出?[使用hashmap 一旦重复则++]
这就叫知己知彼嘛,我得知道自己长啥样,还得知道别人长啥样,然后才能知道有没有人跟我重复,对不对?
好,那我们一个一个来解决,先来思考,我如何才能知道以自己为根的二叉树长啥样?
其实看到这个问题,就可以判断本题要使用 「后序遍历」 框架来解决:
现在,明确了要用后序遍历,那应该怎么描述一棵二叉树的模样呢?我们前文 序列化和反序列化二叉树 其实写过了,二叉树的前序/中序/后序遍历结果可以描述二叉树的结构。
所以,我们可以通过拼接字符串的方式把二叉树序列化[后序遍历一次性解决 重复子树,在节点处输出 重复子树即可],看下代码:
String traverse(TreeNode root) {
// 对于空节点,可以用一个特殊字符表示
if (root == null) {
return "#";
}
// 将左右子树序列化成字符串
String left = traverse(root.left);
String right = traverse(root.right);
/* 后序遍历代码位置 */
// 左右子树加上自己,就是以自己为根的二叉树序列化结果
String subTree = left + "," + right + "," + root.val;
return subTree;
}
我们用非数字的特殊符#表示空指针,并且用字符,分隔每个二叉树节点值,这属于序列化二叉树的套路了,不多说。
注意我们subTree是按照左子树、右子树、根节点这样的顺序拼接字符串,也就是后序遍历顺序。你完全可以按照前序或者中序的顺序拼接字符串,因为这里只是为了描述一棵二叉树的样子,什么顺序不重要。
这样,我们第一个问题就解决了,对于每个节点,递归函数中的subTree变量就可以描述以该节点为根的二叉树。
现在我们解决第二个问题,我知道了自己长啥样,怎么知道别人长啥样?这样我才能知道有没有其他子树跟我重复对吧。
这很简单呀,我们借助一个外部数据结构,让每个节点把自己子树的序列化结果存进去,这样,对于每个节点,不就可以知道有没有其他节点的子树和自己重复了么?
如果出现多棵重复的子树,结果集res中必然出现重复,而题目要求不希望出现重复。
可以使用Map记录子树,我的题解代码如下:
class Solution {
public:
/**
* @Description: 首先:想到看到自身全貌——使用后序遍历递归返回string子树序列化一次性发现自身subTree;然后,全局重复使用 HashMap进行计数,重复则加入ans。
* @param {*}
* @return {*}
* @notes: 【注意:外加一个记录节点的数据结构; 注意 解题时的递归不一定是本身——而是要考虑效率和实用性基础上 ;创造性的开创 helper() 序列化——相信递归定义、知晓根节点做什么;】最后,利用数据结构重复性在根节点处 解题。
*/
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
unordered_map<string, int> subTree;
vector<TreeNode *> ans; // 如果重复则记录当前子树的根节点。
if(root == nullptr) return ans;
helper(root, subTree, ans);
return ans;
}
// 辅助函数 —— 后序遍历序列化所有子树;并判断是否重复 加入节点。
// 【注意:】这里有一个知识点 —— 序列化和反序列化二叉树
string helper(TreeNode* root, unordered_map<string, int>& subTree, vector<TreeNode *>& ans){
if(root == nullptr) return "#";
string left = helper(root->left, subTree, ans);
string right = helper(root->right, subTree, ans);
// 序列化根节点
stringstream ssr;
string a;
ssr << root->val;
ssr >> a;
// 序列化
string curTree = left + ',' + right + ',' + a;
int count = subTree[curTree]++; // 【关键之处】 注意map这里是后++;所以首先count=0; //但是 subTree[curTree] =1 会首先为1。
cout << "now subTree["<< curTree<<"] is:" << subTree[curTree] << endl;
// 防止重复出现
if(count == 1){
// 第二次出现 即重复了 // 题解
ans.push_back(root);
}
return curTree;
}
};
4. c++ 101拓展题目
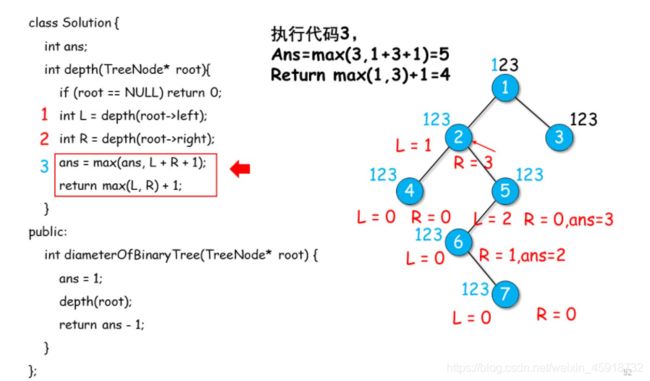
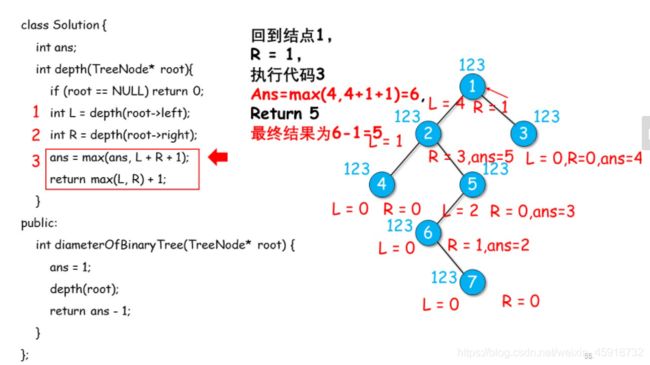
4.1 递归+后序visit–找直径
我的解法:
/**
* @Description: 我看出了递归树的用法【每次都需要维持一个左右最大深度,但是 最终合并为一个路径】,
* 但是没有看出框架方便的实质 —— ①我想从上往下走,但是每次都要O(n^2)复杂度。
* ②但是递归是深搜——最好 从下往上走,【visit是每次比较下,使用max()即可】。
* @Param: D.S. 维持一个深度递归返回深度, 维持当前路径为形参。
* @Return:
* @Notes: 本题最简单的方法:①使用 递归<本质的回传至是树的一侧。>;②在形参处添加 直径进行solution。
* ③注意后序遍历中,因为后序判断完了才 使得当前深度+1;所以到最后 由于左右都是那个高度,没有+1,
* 所以最终结果直接返回即可。
*/
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
// 树的最大路径,变得最长边的距离
int diameter = 0;
findMaxDiaFromDownToFront(root, diameter);
return diameter;
}
// 辅助函数—— 仍然是递归树进行递归和使用。
int findMaxDiaFromDownToFront(TreeNode* root, int& diameter){
// 结束位置
if(root == nullptr){ return 0; }
// 递归和 visit
int l = findMaxDiaFromDownToFront(root->left, diameter), r = findMaxDiaFromDownToFront(root->right, diameter);
// visit 进入递归的最下方——进行处理
// 相当于后续
diameter = max(l+r, diameter); //【注意这里没有 +1 +1 ;所以直接 等于图的直径。当前状态没有加1,返回的时候当前状态的高度才进行加1!】。
return 1 + max(l,r); // 相当于 寻找最大的高度
}
};
4.1.1 注意:上述题目 可以基于下面“寻找二叉树最大深度”的递归来做:
以下三种解法:①深搜,②广搜,③递归<大佬>
// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
/**
* @Description: 深度搜索 找对大深度
* @Param:
* @Return:
* @Notes:
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
//深搜/遍历 找高度
if(root == nullptr) return 0;
int cur = 1, height = 1;
dfs(root->left, cur+1, height);
dfs(root->right, cur+1, height);
return height;
}
void dfs(TreeNode* root, int cur, int& height){
// 边界
if(root == nullptr) {return ;}
// do比较设置
height = cur>height? cur : height;
// 继续深搜
dfs(root->left, cur+1, height);
dfs(root->right, cur+1, height);
}
/**
* @Description: BFS广搜/层次 找高度
* @Param: queue,
* @Return:
* @Notes: 【注意:】在这一题中,广搜和深搜的时间和空间复杂度是一样的。
*/
int maxDepth1(TreeNode* root) {
//visited 不用了
if(root == nullptr) {return 0;}
queue<TreeNode*> q;
int height = 0;
q.push(root);
while(!q.empty()){
// 开始bfs
int sz = q.size();
while(sz--){
TreeNode* a = q.front();
q.pop();
// height
// xunzhao1
// visit
if(a->left != nullptr){
q.push(a->left);
}
if(a->right!=nullptr){
q.push(a->right);
}
}
height++;
}
return height;
}
/**
* @Description: 大佬递归方法。
* @Param:
* @Return:
* @Notes:
*/
int maxDepth2(TreeNode* root) {
// 最大深度
return root? 1 + max(maxDepth(root->left), maxDepth(root->right)): 0 ;
}
};
4.2 路径总和<从上至下>III
首先朴素的想——《画出一个例子》
- 画出例子,在树的框架下用递归:1.找到最简单的子问题求解,2.其他问题不考虑内在细节,只考虑整体逻辑),那我们现在来设计递归关系:
首先,最简单的子问题是什么呢?由于这道题是在树的框架下,我们最容易想到的就是遍历的终止条件:
if(root == null){
return 0;
}
- 接下来,我们来考虑再上升的一个层次,题目要求 路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点) 。这就要求我们只需要去求三部分即可:
以当前节点作为头结点的路径数量
以当前节点的左孩子作为头结点的路径数量
以当前节点的右孩子作为头结点啊路径数量
将这三部分之和作为最后结果即可。
- 最后的问题是:我们应该如何去求以当前节点作为头结点的路径的数量?这里依旧是按照树的遍历方式模板,每到一个节点让sum-root.val,并判断sum是否为0,如果为零的话,则找到满足条件的一条路径。
总体来看:即
- 先序递归遍历每个节点
- 以每个节点作为起始节点DFS寻找满足条件的路径
我的解法一:双重递归:
// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
/**
* @Description:
* @param {int} sum
* @return {*}
* @notes: 【注意】这里的路径说的是,从上往下的路径, 不包括回去绕个 节点的路径!
*/
int pathSum(TreeNode* root, int sum) {
// 前序遍历/深搜 + 自动回溯。
// 全部从上到下 遍历一遍。
if( root == nullptr) return 0;
// visit
int count = dfsAndTrack(root, sum);
// dfs
count += pathSum(root->left, sum);
count += pathSum(root->right, sum);
return count;
}
// 上述辅助函数,对应深搜和track
int dfsAndTrack(TreeNode* root, int sum){
if(root == nullptr) return 0;
// visit
bool flag = false;
if(root->val == sum ) flag = true;
return flag ? 1+dfsAndTrack(root->left, sum-root->val)+dfsAndTrack(root->right, sum-root->val)
: dfsAndTrack(root->left, sum-root->val)+dfsAndTrack(root->right, sum-root->val) ; // 这里注意两边是分别独立的。
}
};
解法二:使用sumlist[] 记录从上往下的路径和
只需一次递归五行代码,用列表记录下当前结果即可,为什么要双重递归呢?
sumlist[]记录当前路径上的和,在如下样例中:
10
/ \
5 -3
/ \
3 2 11
/ \
3 -2 1
当DFS刚走到2时,此时sumlist[]从根节点10到2的变化过程为:
10
15 5
17 7 2
当DFS继续走到1时,此时sumlist[]从节点2到1的变化为:
18 8 3 1
因此,只需计算每一步中,sum在数组sumlist中出现的次数,然后与每一轮递归的结果相加即可
count = sumlist.count(sum)等价于:
count = 0
for num in sumlist:
if num == sum:
count += 1
count计算本轮sum在数组sumlist中出现的次数
class Solution {
public:
int dfs(vector<int>& v,int sum,TreeNode* root)
{
if(root==NULL) return 0;
vector<int> tmp;
int res=0;
for(int i=0;i<v.size();i++)
{
tmp.push_back(v[i]+root->val);
if(tmp.back()==sum) res++;
}
tmp.push_back(root->val);
if(tmp.back()==sum) res++;
return res+dfs(tmp,sum,root->left)+dfs(tmp,sum,root->right);
}
int pathSum(TreeNode* root, int sum) {
vector<int> tmp;
return dfs(tmp,sum,root);
}
};
4.3 删点成林—删除相关【递归提升】
1、后续遍历所有节点,使用Hash表查找是否是需要删除的节点。
2、如果是删除节点,分别把左孩子或右孩子加入到结果中,把父节点的左孩子或右孩子指针置空。
3、如果是根且不需要删除,把根树加入到结果中。
这道题最主要需要注意的细节是如果通过递归处理原树,以及需要在什么时候断开指针。【即递归删除方法?! 递归返回值?!】
形参同时&也需要注意。【根据本质需要 设置。】
同时,为了便于寻找待删除节点,可以建立一个哈希表方便查找。
我的解法:
// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
/**
* @Description: 算法思维:树的框架进行递归 —— 后序遍历方便一次性 加入到ans中。
* @param {*} 设置成unordered_set 方便进行搜索。 vector ans
* @return {*}
* @notes: 注意:【是要根据实际实用的 要求在递归的1、形参2、返回值中使用】 在这里进行删除的关键点是如何给父节点分发nullptr?!所以 返回root指针方便操作。
*/
vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {
//删点成林
vector<TreeNode*> ans;
unordered_set<int> delete_list(to_delete.begin(), to_delete.end());
root = helper(root, delete_list, ans);
if(root){ // 存在
ans.push_back(root);
}
return ans;
}
// helper辅助函数——寻找删除点 并 返回构建树的结果?删除<其中要 注意是中间节点即要加入进去>or原始不变?
TreeNode* helper(TreeNode* root, unordered_set<int> delete_list, vector<TreeNode*> &ans){
// 边界,返回root
if(!root) return root;
// 后序遍历 开始
root->left = helper(root->left, delete_list, ans);
root->right = helper(root->right, delete_list, ans);
// visit
if(delete_list.count(root->val)>0) { //存在
// 中间节点
if(root->left){ ans.push_back(root->left); }
if(root->right){ ans.push_back(root->right); }
return nullptr;
}
// 遍历结束
return root;
}
};
4.4 前序和中序数组来构建二叉树
思路:首先通过分析题目、举出多个例子 —— <通过人工手动构建 知晓>一些前序和中序构建的人脑本质的性质;
接下来,通过这种性质 想一下如何code;给出基本算法思想、数据结构和实现细节。
性质 —— 人工手动构建 知晓
即:前序找根节点;然后中序找分割的左右节点。

基本算法思路
思路
- 构建一个二叉树需要构建三部分:root、左子树、右子树
- 左子树、右子树的构建,又包括:root、左子树、右子树
- 解题关键在于定位出根节点,划分出左右子树,然后 递归 构建左右子树
具体做法 - preorder 数组的第一项肯定是根节点 —— 因为前序遍历的顺序是 根∣左∣右根| 左|右根∣左∣右。
- 根据根节点,在 inorder [左∣根∣右][左 | 根 | 右][左∣根∣右] 中划分出分别属于左、右子树的 inorder 序列。
- 并求出左右子树的节点个数,在 preorder 中划分出分别属于左、右子树的 preorder 序列。
- 于是就有了左、右子树的 preorder 和 inorder 序列,递归构建左、右子树就好。
数据结构和细节—见解法1
解法1:
前序visit处理。后序return。 综合起来 —— 形成递归 —— 综合提升!【重点看!】
查找根节点位置 -> 哈希表
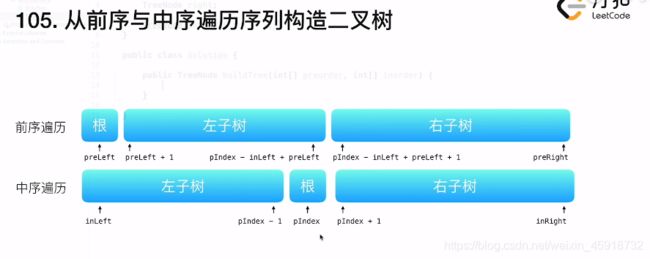
重点就在这几个区间的index怎么算上
首先,中序遍历中确定根节点的index为k, 那么两个子区间分别为[il, k - 1] 和[k + 1, ir]
这样也确定了左子树子区间的长度为k - 1 - il + 1 = k - il, 右子树子区间的长度为ir - (k + 1) + 1 = ir - k
根据这个长度我们可以得到在前序遍历里面两个区间的位置,根节点为 pl
左子树子区间r - (pl + 1) + 1 = k - il -> r = k + pl - il
右子树子区间pr - l + 1 = ir - k -> l = k + pr - ir + 1
我的解法
class Solution {
public:
/**
* @Description: 题目已知前序和中序,如何求 当前的树结构?
* @param {*}
* @return {*}
* @notes:
*/
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
unordered_map<int, int> inorderMap;
for(int i = 0; i<inorder.size() ;i++){
inorderMap[inorder[i]] = i;
}
return helper(preorder, inorderMap, 0, preorder.size()-1, 0, inorder.size()-1);
}
// 辅助函数 —— 递归构建
// 每次都构建根节点,然后 找中间点。 递归构建左右子树。 再回溯后序返回,——最终能返回到root
TreeNode* helper(vector<int>& preorder, unordered_map<int, int> &inorderMap, int preLeft, int preRight, int inLeft, int inRight){
if( preLeft > preRight ) return nullptr;
TreeNode* root = new TreeNode(preorder[preLeft]);
int pivot = inorderMap[preorder[preLeft]];
int num_left = pivot - inLeft, num_right = inRight - pivot;
root->left = helper(preorder, inorderMap, preLeft+1, preLeft+num_left, inLeft, pivot-1);
root->right = helper(preorder, inorderMap, preLeft+num_left+1, preRight, pivot+1, inRight);
return root;
}
};