成成你好呀笔记整理(知识点合集二)
第二十三讲 栈和队列
栈是一种重要的线性结构,可以这样讲,栈是前面讲过的线性表的一种具体形式。
就像我们刚才的例子,栈这种后进先出的数据结构应用是非常广泛的。
在生活中,例如我们的浏览器,每点击一次“后退”都是退回到最近的一次浏览网页。例如我们Word,Photoshop等的“撤销”功能也是如此。
再例如我们C语言的函数,也是利用栈的基本原理实现的。
官方定义:
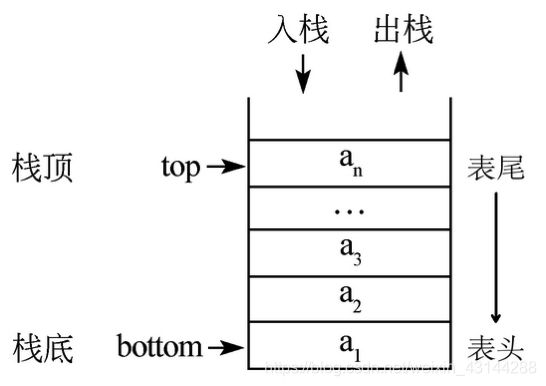
栈(Stack)是一个后进先出(Last in first out,LIFO)的线性表,它要求只在表尾进行删除和插入操作。
小甲鱼定义:
所谓的栈,其实也就是一个特殊的线性表(顺序表、链表)。
但是它在操作上有一些特殊的要求和限制:
栈的元素必须“后进先出”。
栈的操作只能在这个线性表的表尾进行。
对于栈来说,这个表尾称为栈的栈顶(top),相应的表头称为栈底(bottom),现在回看那把手枪,就恍然大悟了吧!
栈的插入操作(Push),叫做进栈,也称为压栈,入栈,类似子弹放入弹夹的动作。
栈的删除操作(Pop),叫做出栈,也称为弹栈。如同弹夹中的子弹出夹。
动画实现:
2.栈的顺序存储结构
因为栈的本质是一个线性表。
线性表有两种存储形式,那么栈也有分为栈的顺序存储结构和栈的链式存储结构。
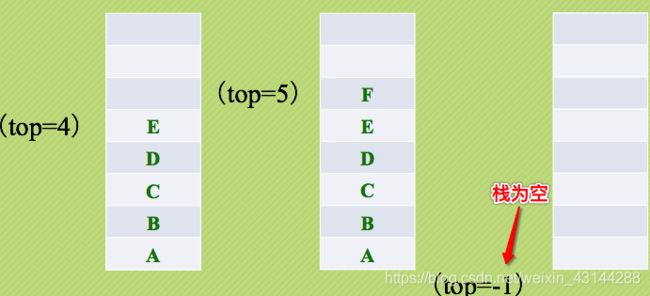
最开始栈中不含有任何数据,叫做空栈,此时栈顶就是栈底。
然后数据从栈顶进入,栈顶栈底分离,整个栈的当前容量变大。
数据出栈时从栈顶弹出,栈顶下移,整个栈的当前容量变小。
妈呀,说啥呢?
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
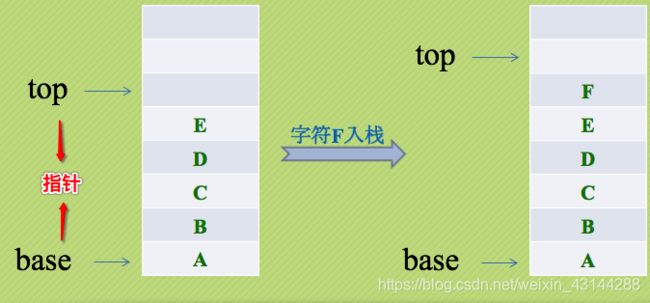
这里定义了一个顺序存储的栈,它包含了三个元素:base、top、stackSize。
◊base是指向栈底的指针变量
◊top是指向栈顶的指针变量
◊stackSize指示栈的当前可使用的最大容量
3.创建一个栈
代码实现:
#define STACK_INIT_SIZE 100
initStack(sqStack *s)
{
s->base = (ElemType *)malloc( STACK_INIT_SIZE * sizeof(ElemType) );
if( !s->base )
exit(0);
s->top = s->base; // 最开始,栈顶就是栈底
s->stackSize = STACK_INIT_SIZE;
}
4.入栈操作
入栈操作又叫压栈操作,就是向栈中存放数据。
入栈操作要在栈顶进行,每次向栈中压入一个数据。
top指针就要+1,知道栈满为止。
代码实现:
#define SATCKINCREMENT 10
Push(sqStack *s, ElemType e)
{
// 如果栈满,追加空间
if( s->top – s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize; // 设置栈顶
s->stackSize = s->stackSize + STACKINCREMENT; // 设置栈的最大容量
}
*(s->top) = e;
s->top++;
}
5.出栈操作
出栈操作就是在栈顶取出数据,栈顶指针随之下移的操作。
每当从栈内弹出一个数据,栈的当前容量就-1。
代码实现
Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base ) // 栈已空空是也
return;
*e = *--(s->top);
}
第二十四讲 栈和队列2 | 【疑问解释】
1.疑问解释
★ 第二十三讲 栈和队列 ★中介绍“栈”的结构,我们是这样声明的:
typedef int ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
热爱学习的鱼油提出了疑问:
怎么没有data元素存放数据?
怎么会有两个ElemType元素?
这是小甲鱼老师的一个套路!
其实如果小甲鱼按照套路出牌,我们完全可以这样子声明:
typedef int ElemType;
typedef struct
{
ElemType data[MAXSIZE];
int top; // 用于标注栈顶的位置
int stackSize;
}
但是呢,小甲鱼要考虑到大家希望学习到的是“不变应万变”的能力!
比较高级的写法,会让人一头雾水,一旦理解却又屡试不爽!
传统套路 Vs 鱼C套路
除了入栈和出栈,还有其他的操作:
例如清空一个栈,销毁一个栈,计算栈的当前容量等。
①清空栈
所谓清空一个栈:
就是将栈中的元素全部作废,但栈本身物理空间并不发生改变(不是销毁)。
因此我们只要将s->top的内容赋值为s->base即可。
这样s->base等于s->top,也就表明这个栈是空的了。
友情提醒:
这个原理跟高级格式化只是但单纯地清空文件列表而没有覆盖硬盘的原理是一样的。
代码清单:
ClearStack(sqStack *s){
s->top = s->base;
}
②销毁一个栈与清空一个栈不同!
销毁一个栈是要释放掉该栈所占据的物理内存空间。
因此不要把销毁一个栈与清空一个栈这两种操作混淆。
代码清单:
DestroyStack(sqStack *s){
int i, len;
len = s->stackSize;
for( i=0; i < len; i++ ){
free( s->base );
s->base++;
}
s->base = s->top = NULL;
s->stackSize = 0;
}
计算栈的当前容量
计算栈的当前容量也就是计算栈中元素的个数,因此只要返回s.top-s.base即可。
注意:
栈的最大容量是指该栈占据内存空间的大小,其值是s.stackSize,它与栈的当前容量不是一个概念哦。
代码清单:
int StackLen(sqStack s)
{
return(s.top – s.base); // 初学者需要重点讲解
}
3.实例分析
题目:
利用栈的数据结构特点,将二进制转换为十进制数。
分析:
地球人都知道,二进制数是计算机数据的存储形式。
它是由一串0和1组成的,每个二进制数转换成相应的十进制数方法如下:
(XnXn-1……X3X2X1)2 = X1*2^0+X2*2^1+…+Xn*2^(n-1)
复制代码
一个二进制数要转换为相应的十进制数,就是从最低位起用每一位去乘以对应位的积。
也就是说用第n位去乘以2^(n-1),然后全部加起来
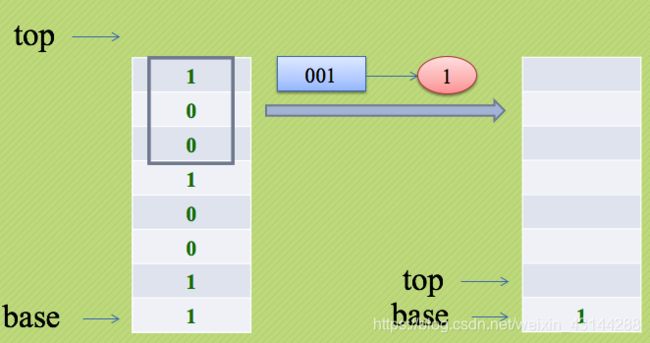
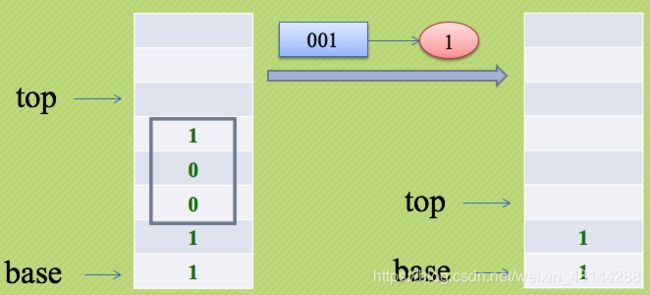
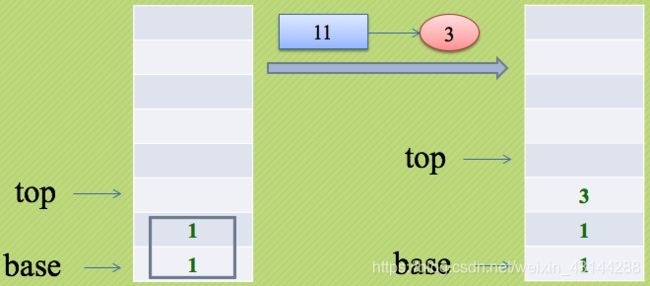
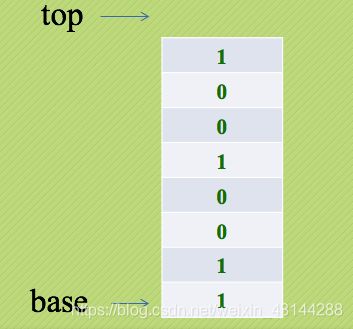
由于栈具有后进先出的特性,例如我们输入11001001这样的二进制数,如图:
第二十五讲 进制转换
1.实例分析
题目:
利用栈的数据结构特点,将二进制(B)转换为十进制(D)数。
分析:
地球人都知道,二进制数是计算机数据的存储形式,它是由一串0和1组成的,每个二进制数转换成相应的十进制数方法如下:
(XnXn-1……X3X2X1)2 = X1*2^0+X2*2^1+…+Xn*2^(n-1)
一个二进制数要转换为相应的十进制数,就是从最低位起用每一位去乘以对应位的积,也就是说用第n位去乘以2^(n-1),然后全部加起来。
由于栈具有后进先出的特性,例如我们输入11001001这样的二进制数,如图:
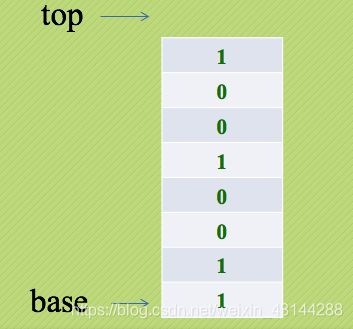
我们学习编程常常会接触到不同进制的数,而最多的就是二进制、八进制、十进制、十六进制。
鱼C人还知道:
二进制是计算机唯一认识的,十进制是人们通常使用的。
那么,有没有谁知道八进制和十六进制呢?
为什么没有三进制、四进制、五六七进制呢?
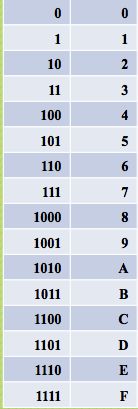
(⊙v⊙)嗯,我们仔细观察二进制跟十六进制的对应关系:
因为早期的计算机系统都是三的倍数,所以用八进制比较方便。
我们发现了,在进行二进制到八进制的转换时,要将二进制数的每三位抓换成一个八进制数来表示,然后按顺序输出即可。
#include
#include
#include
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
typedef char ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
void Push(sqStack *s, ElemType e)
{
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
}
*(s->top) = e;
s->top++;
}
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
{
return;
}
*e = *--(s->top);
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
ElemType c;
sqStack s;
int len, i, sum = 0;
InitStack(&s);
printf("请输入二进制数,输入#符号表示结束!\n");
scanf("%c", &c);
while( c != '#' )
{
Push(&s, c);
scanf("%c", &c);
}
getchar(); // 把'\n'从缓冲区去掉
len = StackLen(s);
printf("栈的当前容量是: %d\n", len);
for( i=0; i < len; i++ )
{
Pop(&s, &c);
sum = sum + (c-48) * pow(2, i);
}
printf("转化为十进制数是: %d\n", sum);
return 0;
}
2.课后训练
①二进制转换成十六进制:
/*****************************/
/** 二进制/十六进制转换器 **/
/** By www.fishc.com 小甲鱼 **/
/*****************************/
#include
#include
#include
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
typedef char ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
// 函数功能:初始化栈
// 参数*s:栈的地址
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
// 函数功能:入栈操作
// 参数*s:栈的地址
// 参数e:待压入栈的元素
void Push(sqStack *s, ElemType e)
{
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e;
s->top++;
}
// 函数功能:弹栈操作
// 参数*s:栈的地址
// 参数e:存放从栈里弹出的数据
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
{
return;
}
*e = *--(s->top);
}
// 函数功能:计算栈s的当前长度
// 参数s:栈
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
ElemType c;
sqStack s1;
sqStack s2;
int len, i, j, sum = 0;
InitStack(&s1); // 初始化栈s1,用来存放二进制输入
printf("请输入二进制数,输入‘#’号表示结束!\n\n");
scanf("%c", &c);
while( c != '#' )
{
if( c=='0' || c=='1' ) // 检查输入是否二进制
Push(&s1, c);
scanf("%c", &c);
}
getchar(); // 把'\n'从缓冲区去掉
len = StackLen(s1);
InitStack(&s2); // 初始化栈s2,用来存放转换的八进制
for( i=0; i < len; i+=4 )
{
for( j=0; j < 4; j++ )
{
Pop( &s1, &c ); // 取出栈顶元素
sum = sum + (c-48) * pow(2, j);
if( s1.base == s1.top )
{
break;
}
}
switch( sum )
{
case 10: sum = 'A'; break;
case 11: sum = 'B'; break;
case 12: sum = 'C'; break;
case 13: sum = 'D'; break;
case 14: sum = 'E'; break;
case 15: sum = 'F'; break;
default: sum += 48;
}
Push( &s2, sum );
sum = 0;
}
printf("\n转化为十六进制数是: ");
while( s2.base != s2.top )
{
Pop( &s2, &c );
printf("%c", c);
}
printf("(H)\n");
return 0;
}
②二进制转换成八进制:
/*****************************/
/** 二进制/八进制转换器 **/
/** By www.fishc.com 小甲鱼 **/
/*****************************/
#include
#include
#include
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
typedef char ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
// 函数功能:初始化栈
// 参数*s:栈的地址
void InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
// 函数功能:入栈操作
// 参数*s:栈的地址
// 参数e:待压入栈的元素
void Push(sqStack *s, ElemType e)
{
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
{
exit(0);
}
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e;
s->top++;
}
// 函数功能:弹栈操作
// 参数*s:栈的地址
// 参数e:存放从栈里弹出的数据
void Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
{
return;
}
*e = *--(s->top);
}
// 函数功能:计算栈s的当前长度
// 参数s:栈
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
ElemType c;
sqStack s1;
sqStack s2;
int len, i, j, sum = 0;
InitStack(&s1); // 初始化栈s1,用来存放二进制输入
printf("请输入二进制数,输入‘#’号表示结束!\n\n");
scanf("%c", &c);
while( c != '#' )
{
if( c=='0' || c=='1' ) // 检查输入是否二进制
Push(&s1, c);
scanf("%c", &c);
}
getchar(); // 把'\n'从缓冲区去掉
len = StackLen(s1);
InitStack(&s2); // 初始化栈s2,用来存放转换的八进制
for( i=0; i < len; i+=3 )
{
for( j=0; j < 3; j++ )
{
Pop( &s1, &c ); // 取出栈顶元素
sum = sum + (c-48) * pow(2, j);
if( s1.base == s1.top )
{
break;
}
}
Push( &s2, sum+48 );
sum = 0;
}
printf("\n转化为八进制数是: ");
while( s2.base != s2.top )
{
Pop( &s2, &c );
printf("%c", c);
}
printf("(O)\n");
return 0;
}
第二十六讲 栈和队列4 | 【逆波兰表达式】
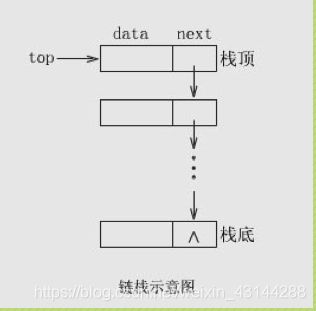
1.栈的链式存储结构
讲完了:
栈的顺序存储结构,也给大家结合了一些例题演练,相信大家对栈再也不陌生了吧?
现在我们来看下栈的链式存储结构(简称栈链)。
栈因为只是栈顶来做插入和删除操作。
所以比较好的方法就是:
将栈顶放在单链表的头部,栈顶指针和单链表的头指针合二为一。
teypedef struct StackNode
{
ElemType data; // 存放栈的数据
struct StackNode *next;
} StackNode, *LinkStackPtr;
teypedef struct LinkStack
{
LinkStackPrt top; // top指针
int count; // 栈元素计数器
}
2.进栈操作
对于栈链的Push操作,假设元素值为e的新结点是s,top为栈顶指针。
我们得到如下代码:
Status Push(LinkStack *s, ElemType e)
{
LinkStackPtr p = (LinkStackPtr) malloc (sizeof(StackNode));
p->data = e;
p->next = s->top;
s->top = p;
s->count++;
return OK;
}
3.出栈操作
至于链栈的出战Pop操作,假设变量p用来存储要删除的栈顶结点。
将栈顶指针下移一位,最后释放p即可。
代码如下:
Status Pop(LinkStack *s, ElemType *e)
{
LinkStackPtr p;
if( StackEmpty(*s) ) // 判断是否为空栈
return ERROR;
*e = s->top->data;
p = s->top;
s->top = s->top->next;
free(p);
s->count--;
return OK;
}
4.终极实践
在讲解这道例题的时候,请允许小甲鱼花一点点的时间对小学时候的数学老师进行感谢:
嗯,谢谢您,让我学会如何计算以下这道表达式,并且认为它十分简单:
(1-2)*(4+5)
人类早就熟悉这种中缀表达式的计算方式,因为括号里边的要先进行计算。
但是计算机不喜欢了,因为我们有小括号中括号大括号,还允许一个嵌套一个。
这样子计算机就要进行很多次if判断才行决定哪里先计算。
那怎么办呢?
逆波兰表达式
在20世纪三十年代,波兰逻辑学家Jan.Lukasiewicz灵感闪现,然后发明了一种不需要括号的后缀表达式。
我们通常把它称为逆波兰表达式(RPN) 。
先来看看,对于(1-2)*(4+5),如果用逆波兰表示法,应该是这样:
1 2 – 4 5 + *
这种方式敢情我们人类是不大好接受的了,不过对于计算机来说,那可是喜爱至极。
因为只需要利用栈的特点,就可以将这种后缀表达式的性能发挥到极致。
解析来就让小甲鱼图文并茂的解释一下吧!
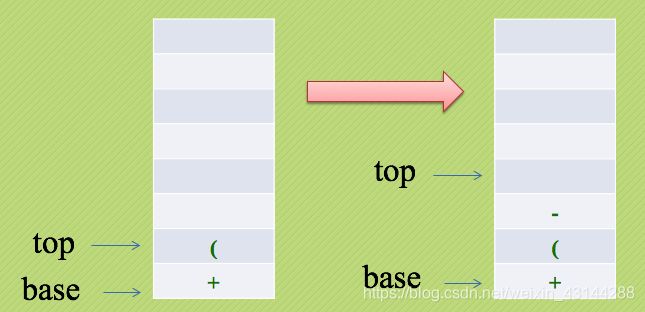
数字1和2进栈,遇到减号运算符则弹出两个元素进行运算并把结果入栈。
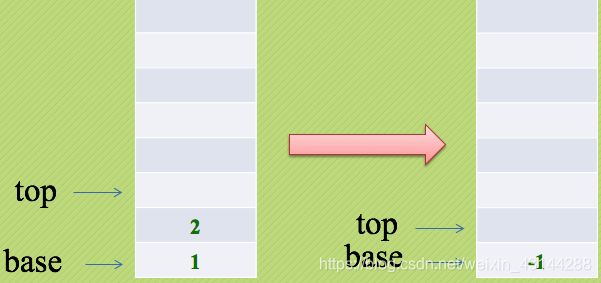
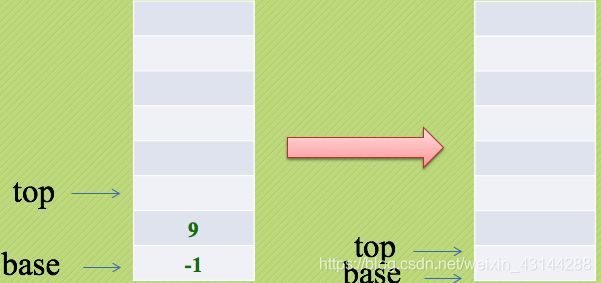
4和5入栈,遇到加号运算符,4和5弹出栈,相加后将结果9入栈。

然后又遇到乘法运算符,将9和-1弹出栈进行乘法计算,此时栈空并无数据压栈,-9为最终运算结果!
第二十七讲 栈和队列5 | 【逆波兰计算器实战】
1.逆波兰计算器
这节课小甲鱼带大家一起写一个逆波兰计算器,需要实现以下要求:
实现对逆波兰输入的表达式进行计算。
支持带小数点的数据。
正常的表达式 —> 逆波兰表达式:
a+b ---> a b +
a+(b-c) ---> a b c - +
a+(b-c)*d ---> a b c - d * +
a+d*(b-c)---> a d b c - * +
本节为手把手实操课,请大家认真观看视频
代码实操:
#include
#include
#include
#define STACK_INIT_SIZE 20
#define STACKINCREMENT 10
#define MAXBUFFER 10
typedef double ElemType;
typedef struct
{
ElemType *base;
ElemType *top;
int stackSize;
}sqStack;
InitStack(sqStack *s)
{
s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base;
s->stackSize = STACK_INIT_SIZE;
}
Push(sqStack *s, ElemType e)
{
// 栈满,追加空间,鱼油必须懂!
if( s->top - s->base >= s->stackSize )
{
s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
if( !s->base )
exit(0);
s->top = s->base + s->stackSize;
s->stackSize = s->stackSize + STACKINCREMENT;
}
*(s->top) = e; // 存放数据
s->top++;
}
Pop(sqStack *s, ElemType *e)
{
if( s->top == s->base )
return;
*e = *--(s->top); // 将栈顶元素弹出并修改栈顶指针
}
int StackLen(sqStack s)
{
return (s.top - s.base);
}
int main()
{
sqStack s;
char c;
double d, e;
char str[MAXBUFFER];
int i = 0;
InitStack( &s );
printf("请按逆波兰表达式输入待计算数据,数据与运算符之间用空格隔开,以#作为结束标志: \n");
scanf("%c", &c);
while( c != '#' )
{
while( isdigit(c) || c=='.' ) // 用于过滤数字
{
str[i++] = c;
str[i] = '\0';
if( i >= 10 )
{
printf("出错:输入的单个数据过大!\n");
return -1;
}
scanf("%c", &c);
if( c == ' ' )
{
d = atof(str);
Push(&s, d);
i = 0;
break;
}
}
switch( c )
{
case '+':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d+e);
break;
case '-':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d-e);
break;
case '*':
Pop(&s, &e);
Pop(&s, &d);
Push(&s, d*e);
break;
case '/':
Pop(&s, &e);
Pop(&s, &d);
if( e != 0 )
{
Push(&s, d/e);
}
else
{
printf("\n出错:除数为零!\n");
return -1;
}
break;
}
scanf("%c", &c);
}
Pop(&s, &d);
printf("\n最终的计算结果为:%f\n", d);
return 0;
}
// 5 - (6 + 7) * 8 + 9 / 4
// 5 - 13 * 8 + 9 / 4
// 5 - 104 + 2.25
// -99 + 2.25
// 5 6 7 + 8 * - 9 4 / +
第二十八讲 中缀表达式转换为后缀表达式 | 【附方法论】
1.课前谈一谈
很多鱼油会问:
数据结构和算法到底有没有用
接近答案前的思考:
在大厦的防震设计、消除疾病、防止水源枯竭这些实际问题中,数据结构和算法几乎起不到任何直接作用。。。。。。
那为什么我们要学呢?
答案:
它可以锻炼我们的“高级”思维!
何为高级:
算法的重要性不用说大家都知道,一个程序,特别是大型程序,优秀的算法和架构跟一般的算法和架构效率差别是千万倍!
这就可以解释为什么国产的几大应用都在前几天相继投入血本进行重构。
这就跟建高楼大厦要打好根基是一个道理,很多人喜欢当“暴发户”,根基没打好就开始盖房,但盖到四五层的时候发现根基不稳,拆掉重盖!
一点吹水:
德不配位,必有殃灾
从编程的角度解释这句话,‘德’就是我们编程的基本功,就是数据结构和算法这样的底层知识,你没有打牢,后果一旦发生,苦痛滋味一尝便知。
2.中缀表达式转换为后缀表达式
我们人类确实是喜欢这样的表达式:
(1-2)*(4+5)
而不是这样的:
1 2 – 4 5 + *
所以,我们这节课的任务就是编写一个程序:
将用户输入的中缀表达式转换为后缀表达式,而作为课后作业的延生,要求大家动手写一个中缀表达式计算器!
那么如何将“(1-2)*(4+5)”转化为“1 2 – 4 5 + *”呢?
其实很简单:
利用栈的“记忆”吧,符号都推入栈即可。
看图识字环节
为了使得问题变得更加复杂,我们把假想敌设为:
1+(2-3)*4+10/5
第一个输入是数字1,数字在后缀表达式中都是直接输出。
第二个是符号“+”,入栈:
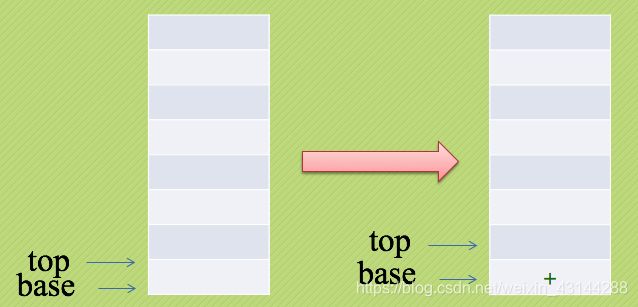
第三个字符是“(”,依然是符号,入栈。
第四个是数字2,输出,然后是符号“-”,入栈:
此时,我们需要去匹配栈里的“(”。
然后再匹配前将栈顶数据依次出栈(这就好比括号里优先执行的道理):
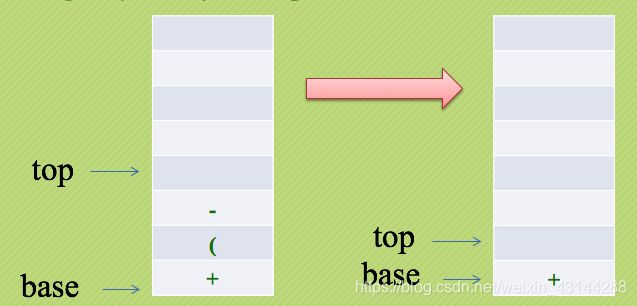
紧接着是符号“*”,直接入栈:
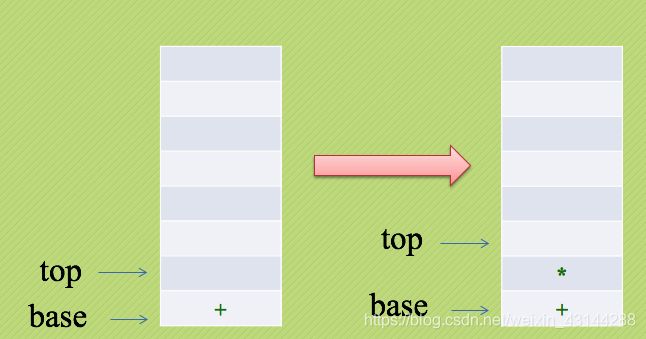
遇到数字4,输出,之后是符号“+”。
此时栈顶元素是符号“*”,按照先乘除后加减原理。
此时栈顶的乘号优先级比即将入栈的加好要大,所以出栈。
栈中第二个元素是加好,按理来说大家平起平坐。
但是按照先到先来后到吃屎的原则,栈里的加好呆得太久了,也要出栈透透气。
(同理如果栈里还有其他操作符,也是出栈)
最后把刚刚吃屎的那个加好入栈,操作如下图:
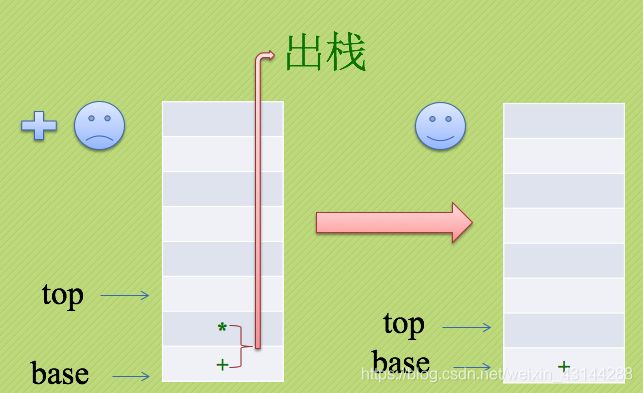
紧接着数字10,输出,最后是符号“/”,进栈:
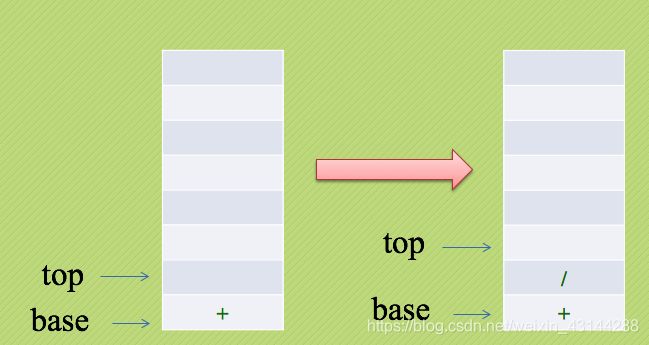
最后一个数字5,输出,所有的输入处理完毕。
但是栈中仍然有数据,所以将栈中符号依次出栈。
有些东西看上去很难,但事实上做起来会更加的麻烦。例如:
就像这道题小甲鱼要求大家务必经过自己的思考,再跟着小甲鱼来打代码,一定会有更大的收获!
总结规则:
从左到右遍历中缀表达式的每个数字和符号,若是数字则直接输出。
若是符号,则判断其与栈顶符号的优先级,是右括号或者优先级低于栈顶符号,则栈顶元素依次出栈并输出,直到遇到左括号或栈空才将吃屎的那个符号入栈。
第二十九讲 队列
队列:
只允许在一端进行插入操作,而在另一端进行删除操作的线性表。
与栈相反,队列是一种先进先出(First In First Out, FIFO)的线性表。
与栈相同的是,队列也是一种重要的线性结构,实现一个队列同样需要顺序表或链表作为基础。

此前我们用浏览器的历史记录作为栈的例子让大家了解她的应用广泛,队列在现实中也是应用十分广泛。
我们的输入缓冲区接受键盘的输入就是按队列的形式输入和输出的,不然的话就很容闹出问题。
例如:
有一天你突然心血来潮,用微信发了一句“You are my god”给你女朋友,表示她就是你的全部。
但是输入缓冲区在输入god这个单词的时候不用队列这个结构而用栈的结构。
就变成了“You are my dog”发出去了。。。。。。
恭喜你,又能单身了。。。
2.队列的链式存储结构
队列既可以用链表实现,也可以用顺序表实现。
跟栈相反的是:
栈一般我们用顺序表来实现,而队列我们常用链表来实现,简称为链队列。
代码:
typedef struct QNode {
ElemType data;
struct QNode *next;
} QNode, *QueuePrt;
typedef struct {
QueuePrt front, rear; // 队头、尾指针
} LinkQueue;
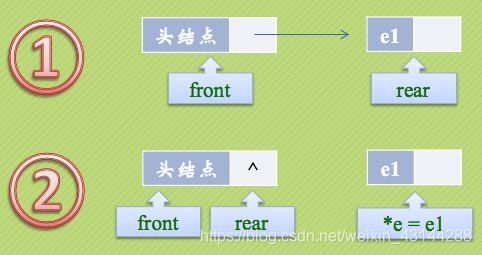
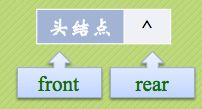
我们将队头指针指向链队列的头结点,而队尾指针指向终端结点。
(注:头结点不是必要的,但为了方便操作,我们加上了。)

空队列时,front和rear都指向头结点。
3.创建一个队列
创建一个队列要完成两个任务:
一是在内存中创建一个头结点。
二是将队列的头指针和尾指针都指向这个生成的头结点,因为此时是空队列。
代码:
initQueue(LinkQueue *q)
{
q->front=q->rear=(QueuePtr)malloc(sizeof(QNode));
if( !q->front )
exit(0);
q->front->next = NULL;
}
4.入队列的操作
InsertQueue(LinkQueue *q, ElemType e)
{
QueuePtr p;
p = (QueuePtr)malloc(sizeof(QNode));
if( p == NULL )
exit(0);
p->data = e;
p->next = NULL;
q->rear->next = p;
q->rear = p;
}
5.出队列的操作
出队列操作是将队列中的第一个元素移出,队头指针不发生改变,改变头结点的next指针即可。
过程如下:
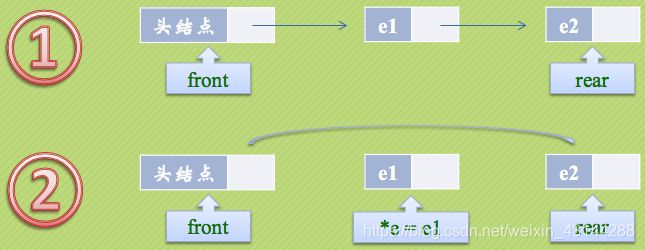
如果原队列只有一个元素,那么我们就应该处理一下队尾指针。
DeleteQueue(LinkQueue *q, ELemType *e)
{
QueuePtr p;
if( q->front == q->rear )
return;
p = q->front->next;
*e = p->data;
q->front->next = p->next;
if( q->rear == p )
q->rear = q->front;
free(p);
}
6.销毁一个队列
由于链队列建立在内存的动态区。
因此当一个队列不再有用时应当把它及时销毁掉,以免过多地占用内存空间。
代码:
DestroyQueue(LinkQueue *q)
{
while( q->front ) {
q->rear = q->front->next;
free( q->front );
q->front = q->rear;
}
}
7.课后作业
要求:
编写一个链队列,任意输入一串字符,以#作为结束标志,然后将队列中的元素显示到屏幕上。
答案:
#include
#include
typedef char ElemType;
typedef struct QNode
{
ElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct
{
QueuePtr front, rear;
} LinkQueue;
initQueue(LinkQueue *q)
{
q->front = q->rear = (QueuePtr)malloc(sizeof(QNode));
if( !q->front )
exit(0);
q->front->next = NULL;
}
InsertQueue(LinkQueue *q, ElemType e)
{
QueuePtr p;
p = (QueuePtr)malloc(sizeof(QNode));
if( !q->front )
exit(0);
p->data = e;
p->next = NULL;
q->rear->next = p;
q->rear = p;
}
DeleteQueue(LinkQueue *q, ElemType *e)
{
QueuePtr p;
if( q->front == q->rear )
return;
p = q->front->next;
*e = p->data;
q->front->next = p->next;
if( q->rear == p )
{
q->rear = q->front;
}
free(p);
}
int main()
{
ElemType e;
LinkQueue q;
initQueue(&q);
printf("请输入一个字符串,以井号键结束输入:");
scanf("%c", &e);
while( e != '#' )
{
InsertQueue( &q, e );
scanf("%c", &e);
}
printf("打印队列中的元素:");
while( q.front != q.rear )
{
DeleteQueue( &q, &e );
printf("%c", e);
}
return 0;
}
第三十讲 队列2 | 【附人生如栈鸡汤】
1.队列的顺序存储结构
为什么小甲鱼上节课说:
队列的实现上我们更愿意用链式存储结构来存储?
我们先按照应有的思路来考虑下如何构造队列的顺序存储结构,然后发掘都遇到了什么麻烦。
我们假设:
一个队列有n个元素,则顺序存储的队列需建立一个大于n的存储单元,并把队列的所有元素存储在数组的前n个单元,数组下标为0的一端则是队头。
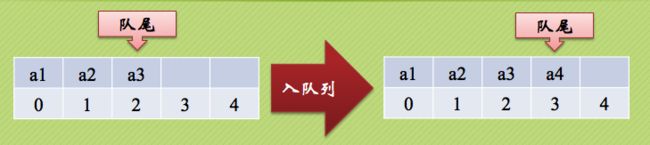
入队列操作其实就是在队尾追加一个元素,不需要任何移动,时间复杂度为O(1)。
出队列则不同,因为我们已经架设下标为0的位置是队列的队头,因此每次出队列操作所有元素都要向前移动。
一群人在排队买火车票,前边的人买好了离开,后面的人就要全部向前一步补上空位。
可是我们研究数据结构和算法的一个根本目的就是要想方设法提高我们的程序的效率。
按刚才的方式,出队列的时间复杂度是O(n),效率大打折扣!
如果我们不去限制队头一定要在下标为0的位置,那么出队列的操作就不需要移动全体元素。

但是这样也会出现一些问题,例如按下边的情形继续入队列,就会出现数组越界的错误。

可事实上我们有0和1两个下标还空着,这叫假溢出。
2.循环队列的定义
我们再想想:
要解决假溢出的办法就是如果后面满了,就再从头开始,也就是头尾相接的循环。
循环队列它的容量是固定的,并且它的队头和队尾指针都可以随着元素入出队列而发生改变。
这样循环队列逻辑上就好像是一个环形存储空间。
但要注意:
在实际的内存当中,不可能有真正的环形存储区,我们只是用顺序表模拟出来的逻辑上的循环。
我们通过一段动画片来加深印象吧!
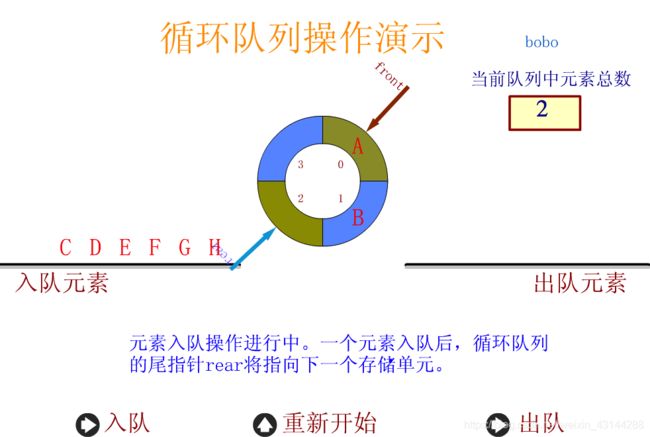
图解:
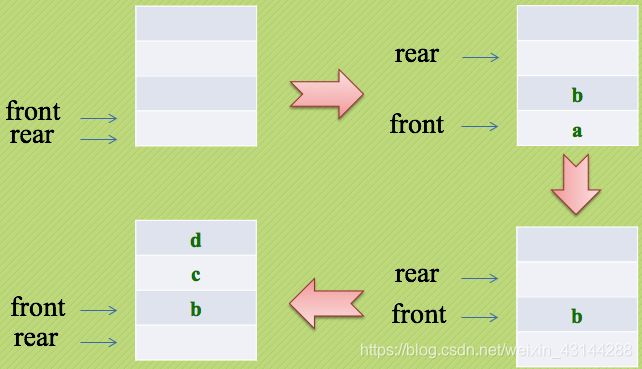
于是我们发觉了,似乎循环队列的实现只需要:
灵活改变front和rear指针即可。
也就是让front或rear指针不断加1,即时超出了地址范围,也会自动从头开始。
我们可以采取取模运算处理:
(rear+1) % QueueSize
(front+1) % QueueSize
取模就是取余数的意思,他取到的值永远不会大于除数,大家结合实例拿张纸算一算就知道了。
3.代码清单
①定义一个循环队列:
#define MAXSIZE 100
typedef struct
{
ElemType *base; // 用于存放内存分配基地址
// 这里你也可以用数组存放
int front;
int rear;
}
②初始化一个循环队列:
initQueue(cycleQueue *q)
{
q->base = (ElemType *) malloc (MAXSIZE * sizeof(ElemType));
if( !q->base )
exit(0);
q->front = q->rear = 0;
}
③入队列操作:
InsertQueue(cycleQueue *q, ElemType e)
{
if( (q->rear+1)%MAXSIZE == q->front )
return; // 队列已满
q->base[q->rear] = e;
q->rear = (q->rear+1) % MAXSIZE;
}
④出队列操作:
DeleteQueue(cycleQueue *q, ElemType *e)
{
if( q->front == q->rear )
return ; // 队列为空
*e = q->base[q->front];
q->front = (q->front+1) % MAXSIZE;
}