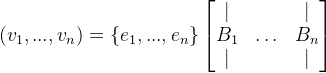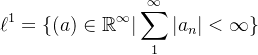代数——第3章——向量空间
第三章 向量空间(Vector Spaces)
fmmer mit den einfachsten Beispielen anfangen.
(始终从最简单的例子开始。)
------------------------------David Hilbert
3.1  (R^n)的子空间
(R^n)的子空间
我们的向量空间的基础模型(本章主题)是n 维实向量空间 ![]() 的子空间。我们将在本节讨论它。向量空间的定义将在3.3节中给出。尽管行向量占据更少的空间,但矩阵乘法的定义使得使用列向量更为便捷,因此,我们通常使用列向量。有时候,为了节省空间,我们使用矩阵的转置(transpose)形式
的子空间。我们将在本节讨论它。向量空间的定义将在3.3节中给出。尽管行向量占据更少的空间,但矩阵乘法的定义使得使用列向量更为便捷,因此,我们通常使用列向量。有时候,为了节省空间,我们使用矩阵的转置(transpose)形式 ![]() 来书写列向量。如在第1章中所述,我们不区分列向量和具有相同坐标的
来书写列向量。如在第1章中所述,我们不区分列向量和具有相同坐标的 ![]() 的点。通常用小写字母来表示列向量,例如,v 或w ,且若
的点。通常用小写字母来表示列向量,例如,v 或w ,且若 ![]() ,我们称
,我们称 ![]() 为 v 的坐标向量(coordinate vector)。
为 v 的坐标向量(coordinate vector)。
我们考虑向量上的2种运算:
(3.1.1)
标量乘法(scalar multiplication):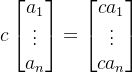 。
。
这些运算使得 ![]() 成为向量空间。
成为向量空间。
对于 ![]() (3.1.1)的一个子集,如果它满足随后所列出的这些属性,则称其为一个子空间(a subspace)。这些属性为:
(3.1.1)的一个子集,如果它满足随后所列出的这些属性,则称其为一个子空间(a subspace)。这些属性为:
(3.1.2)
(a) 若 w 和 w’ 在 W 中,则其和 w + w’ 在 W 中 。
(b) 若 w 在 W 中且 c在ℝ 中,则 cw 在W 中。
(c) 0 向量在 W 中。
还有另一种方式可表述子空间的条件:
(3.1.3) 若 W 非空,且若 ![]() 是 W 的元素,而
是 W 的元素,而 ![]() 是标量,则其线性组合
是标量,则其线性组合 ![]() 也在W 中。
也在W 中。
齐次(homogeneous) 线性方程组(system)提供了子空间的例子。已知一个m × n 矩阵 A 及其位于 ℝ 中的系数,位于 ![]() 中且其坐标向量可作为齐次线性方程组 AX = 0 的解的向量集构成一个子空间,并称其为A的零空间(nullspace)。尽这这个例子很简单,我们还是验证一下它作为子空间所应满足的条件:
中且其坐标向量可作为齐次线性方程组 AX = 0 的解的向量集构成一个子空间,并称其为A的零空间(nullspace)。尽这这个例子很简单,我们还是验证一下它作为子空间所应满足的条件:
![]() AX = 0 且 AY = 0 意味着 A( X + Y ) = 0 :若X和Y是方程的解,则 X + Y 也是方程的解。
AX = 0 且 AY = 0 意味着 A( X + Y ) = 0 :若X和Y是方程的解,则 X + Y 也是方程的解。
![]() AX = 0意味着 AcX = 0:当X是方程的解时,cX也是方程的解。
AX = 0意味着 AcX = 0:当X是方程的解时,cX也是方程的解。
![]() AX = 0 :零向量是方程的一个解。
AX = 0 :零向量是方程的一个解。
零空间 W = 0 和 全空间 ![]() 都是子空间。如果一个子空间不是前面二者之一,则称其为真子空间(proper subspace)。下一个命题描述了
都是子空间。如果一个子空间不是前面二者之一,则称其为真子空间(proper subspace)。下一个命题描述了 ![]() 的真子空间。
的真子空间。
命题 3.1.4 令 W 为 ![]() 的真子空间,令 w 为 W 中的一个非零向量。则 W 由 w 的标量乘组成。不同的真子空间仅有的共同向量是零向量。
的真子空间,令 w 为 W 中的一个非零向量。则 W 由 w 的标量乘组成。不同的真子空间仅有的共同向量是零向量。
一个已知非零向量 w的标量乘cw构成的子空间被称为w所张成的(spanned)(译注:“span”译为“生成”或“张成”,在下文中我们采用“张成”这个译名)子空间。在几何上,它是位于平面 ![]() 上穿过原点的一条直线。
上穿过原点的一条直线。
证明:
我们首先注意到,被一个非零向量w所张成的子空间W,同时也被其所含的另一个非零向量w’ 所张成。这个事实是显然的,因为若 w’ = cw 且 c ≠ 0 ,则任意倍数 aw 都可以写为 ![]() 的形式。因此(Consequently),若被
的形式。因此(Consequently),若被 ![]() 和
和 ![]() 所张成的子空间
所张成的子空间 ![]() 和
和 ![]() 具有一个公共的非零元素 v,则它们相等。
具有一个公共的非零元素 v,则它们相等。
其次,![]() 的一个非零子空间 W 含有一个非零元素
的一个非零子空间 W 含有一个非零元素 ![]() 。因为 W 是一个子空间,它包含由
。因为 W 是一个子空间,它包含由 ![]() 所张成的子空间
所张成的子空间 ![]() ,若
,若 ![]() ,则 W 由一个非零向量的标量乘构成。我们证明,若 W 不等于
,则 W 由一个非零向量的标量乘构成。我们证明,若 W 不等于 ![]() ,则它是整个空间
,则它是整个空间 ![]() 。令
。令 ![]() 为一个W 的不在
为一个W 的不在 ![]() 中的元素,并令
中的元素,并令 ![]() 为由
为由 ![]() 所张成的子空间。因为
所张成的子空间。因为 ![]() ,这些子空间仅有 0 交集。因此,这两个元素
,这些子空间仅有 0 交集。因此,这两个元素 ![]() 和
和 ![]() 都不是对方的倍数。则
都不是对方的倍数。则 ![]() 的坐标向量( 称其为
的坐标向量( 称其为 ![]() )不是成比率关系的,而由这些向量作为列向量的 2×2 块矩阵
)不是成比率关系的,而由这些向量作为列向量的 2×2 块矩阵 ![]() 具有一个非零矩阵。那样话,我们可以解出一个任意向量v的坐标向量B的方程 AX = B ,从而获得线性组合
具有一个非零矩阵。那样话,我们可以解出一个任意向量v的坐标向量B的方程 AX = B ,从而获得线性组合 ![]() 。这就证明了 W 是整个空间
。这就证明了 W 是整个空间 ![]() 。
。
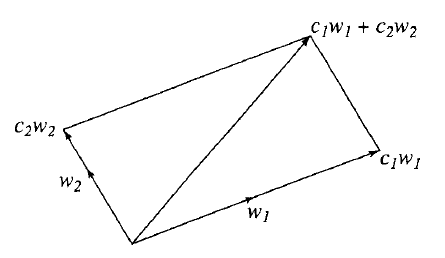
在几何上,根据向量加的平行四边行法则(parallelogram law),也可以观察到每一个向量都是一个线性组合 ![]() 。
。
我们已经给出的 ![]() 子空间的描述将在3.4节通过维度的概念加以阐明。
子空间的描述将在3.4节通过维度的概念加以阐明。
3.2 域(FIELDS)
正如第一章的开头所述,基本上,我们提到的所有关于矩阵的运算,对于复数矩阵和实数矩阵同样适用。对于很多其它的数值系统,同样适配良好。为了便于描述这些数值系统,我们列出所需的“标量”属性,并导出域的概念。在转向向量空间学习之前,我们在这里引入域的概念,这是本章学习的主旨。
复数域 ℂ 的子域是所描述的最简单的域。一个 ℂ 的子域(subfield)是一个子集,它在加,减,乘,和除四种运算下闭合且包含元素1 。换句话说,如果 F 是ℂ的一个子域,它一定满足如下属性(译注:所谓“闭合(closed)”, 即在某种运算下其结果仍然在这个集合中):
(3.2.1) (+, - ,×, ÷ )
![]() 若 a 和 b 在 F 中,则 a + b也在 F 中。
若 a 和 b 在 F 中,则 a + b也在 F 中。
![]() 若 a 在 F 中,则 - a 也在 F 中。
若 a 在 F 中,则 - a 也在 F 中。
![]() 若 a 和 b 在 F 中,则 ab也在 F 中。
若 a 和 b 在 F 中,则 ab也在 F 中。
![]() 若 a 在 F 中且 a ≠ 0 ,则
若 a 在 F 中且 a ≠ 0 ,则 ![]() 在 F 中。
在 F 中。
![]() 1 在F 中。
1 在F 中。
这些公理意味着 1 – 1 也在 F 中。换一种表述,即,F 是加法群 ![]() 的一个子群,且F的非零元素构成一个乘法群
的一个子群,且F的非零元素构成一个乘法群 ![]() 的子群。
的子群。
ℂ 的子域的一些例子:
(a) 实数域 ℝ,
(b) 比率数(整数构成的分数,即分子分母均为整数的分数)域ℚ,
(c) 形如 ![]() 且 a 和 b 为比率数的所有复数的域
且 a 和 b 为比率数的所有复数的域 ![]() 。
。
抽象域(abstract field)的概念仅比子域的概念稍难理解,并且它包含重要的新域类,包括有限域。
定义 3.3.2 一个域F是一个集合与两个合成律
![]() ( 称为加:a ,b ⇝ a + b)
( 称为加:a ,b ⇝ a + b)
和
![]() ( 称为乘:a ,b ⇝ ab)
( 称为乘:a ,b ⇝ ab)
的结合体。并且这两个合成律满足如下公理:
( i ) 这个加法合成律使用 F 成为一个Abel群 ![]() ;它的玄元元素用0表示。
;它的玄元元素用0表示。
( ii ) 这个乘法合成律是可交换的,并使得F的非零元素集合成为一个Abel群 ![]() ;其玄元元素用1表示。
;其玄元元素用1表示。
( iii ) 满足分配律:对于F中的任意a ,b和 c ,都有 a( b + c ) = ab + ac 。
前两个公理分别描述了加法和乘法这两个合顾律的性质。第三个公理,即分配律,将这两个定律联系起来。
您会熟悉实数满足这些公理的事实,但只有在经过一些经验后才能理解这个事实——实数是常规代数运算唯一的需要。
下面的引理解释了0元素如何相乘。
引理 3.2.3 令 F 为一个域。
(a) F 的元素 0 和元素 1 是不同的。
(b) 对于 F 中的任意a,有 a0 = 0 且 0a = 0 。
(c) F 中的乘法是可结合的,且 1 是玄元元素。
证明:
(a) 上面的公理 ( ii ) 意味着 1 不等于 0 。
(b) 对于加法而言,0 是玄元,0 + 0 = 0 。则 a0 + a0 = a( 0 + 0 ) = a0 。因为 ![]() 是一个群,我们可以消去 a0 ,从而得到 a0 = 0 ,以及 0a = 0 。
是一个群,我们可以消去 a0 ,从而得到 a0 = 0 ,以及 0a = 0 。
(c) 因为 F – {0}是一个Abel群,当严格限定在这个子集内的时候,乘法是可结合的。当元素中至少有一个为零时,我们需要证明 a(bc) = (ab)c。在这种情况下,(b) 证明了问题中的乘积等于0 。最后,元素1 是 F – {0} 上的玄元。在 (b) 中设 a = 1 便证明了1是所有F 的玄元。
除了复数的子域之外,域的最简单例子是某些称为素域(prime field)的有限域,我们接下来将对其进行描述。我们在前一章中看到,以整数 n 为模的同余类集合 ℤ/nℤ 具有从整数的加法和乘法导出的加法律和乘法律。除了乘法要求逆元存在之外,域的公理对于所有整数成立。正如第 2.9 节所述,此类公理适用于同余类的加法和乘法。但在整数除法下并不闭合,因此没有理由假设同余类具有乘法逆元。事实上他们不需要。例如,2类没有模 6 的乘法逆元。令人有些惊讶的是,当 p 是素数时,所有模 p 的非零同余类都有逆元,因此集合 ℤ/nℤ 是一个域。这个域称为素域(prime field),并使用符号 ![]() 表示。
表示。
使用上划线记法并选取 p 同余类的常规表示元素,记为
(3.2.4) ![]() 。
。
定理 3.2.5 令 p 为一个素数。每一个模 p 非零同余类都有一个乘法逆元,因此,![]() 是一个 p 阶域。
是一个 p 阶域。
在给出其证明之前,我们先讨论定理。
若 a 和b是整数,则 ![]() 意味着 p 不整除a ,且
意味着 p 不整除a ,且 ![]() 意味着 ab ≡ 1 modulo p 。如果 p 很小,则可以通过试错法求得一个同余类
意味着 ab ≡ 1 modulo p 。如果 p 很小,则可以通过试错法求得一个同余类 ![]() 模p 的逆元。若 p = 13 且
模p 的逆元。若 p = 13 且 ![]() ,则
,则 ![]() ,且
,且 ![]() 。我们是幸运的:
。我们是幸运的: ![]() 的阶为3,因为
的阶为3,因为 ![]() 。在另一方面,6的幂贯穿每一个非零模13同余类。计算幂可能不是求得
。在另一方面,6的幂贯穿每一个非零模13同余类。计算幂可能不是求得 ![]() 逆元的最快方式。但是这个定理告诉我们构成一个群的非零同余类的集合
逆元的最快方式。但是这个定理告诉我们构成一个群的非零同余类的集合 ![]() 。因此,
。因此, ![]() 的每一个元素
的每一个元素 ![]() 都具有限阶,并且,若
都具有限阶,并且,若 ![]() 有阶 r ,则其逆元将是
有阶 r ,则其逆元将是 ![]() 。
。
为了使用这个推理来证明这个定理,我们还需要下面的消去律:
命题 3.2.7 消去律(Cancelation Law):令p为一个素数,并令 ![]() ,
,![]() 和
和 ![]() 为
为 ![]() 的元素。
的元素。
(a) 若 ![]() ,则
,则 ![]() 或
或 ![]() 。
。
(b) 若 ![]() 且若
且若 ![]() ,则
,则 ![]() 。
。
证明:
(a) 我们用整数 a 和 b 来表示同余类 ![]() 和
和 ![]() ,并转化为同余。要证明的知论断是,若p整除 ab ,则 p整除 a 或 p整除 b 。这是推论 2.3.7 ,因此,得证。
,并转化为同余。要证明的知论断是,若p整除 ab ,则 p整除 a 或 p整除 b 。这是推论 2.3.7 ,因此,得证。
(b) 从(a)可以推导出,若 ![]() 且
且 ![]() ,则
,则 ![]() 。
。
定理 (3.2.5)的证明:
令 ![]() 为
为 ![]() 的一个非零元素。我们考虑幂
的一个非零元素。我们考虑幂 ![]() , 因为存在无限多个指数且仅有有限多个元素在
, 因为存在无限多个指数且仅有有限多个元素在 ![]() 中,则,一定有两个幂是相等的,比如说,
中,则,一定有两个幂是相等的,比如说, ![]() , 其中,m < n ,我们在等式两侧消去
, 其中,m < n ,我们在等式两侧消去 ![]() 。则
。则 ![]() 便是
便是 ![]() 的逆元。
的逆元。
在接下来的内容中,将字母上的上划线删去会更方便,相信我们自己能记住我们正在使用整数还是同余类,并记住规则(2.9.8):
若 a 和 b是整数,则在 ![]() 中 a = b 指的是 a ≡ b modulo p 。
中 a = b 指的是 a ≡ b modulo p 。
与通常的同余一样,除了不能在整数中进行除法之外,域 ![]() 中的计算可以通过使用整数来完成。可以使用其列值(entries)位于域中的矩阵 A 进行操作,并且可以重复第一章的讨论而无需进行本质的更改。
中的计算可以通过使用整数来完成。可以使用其列值(entries)位于域中的矩阵 A 进行操作,并且可以重复第一章的讨论而无需进行本质的更改。
假设我们要求素数域 ![]() 中 n 个未知数的 n 阶线性方程组的解。我们用整数系统表示方程组,选择同余类的代表,例如 AX = B,其中 A 是 n × n 整数矩阵,B 是整数列向量。为了解这个
中 n 个未知数的 n 阶线性方程组的解。我们用整数系统表示方程组,选择同余类的代表,例如 AX = B,其中 A 是 n × n 整数矩阵,B 是整数列向量。为了解这个 ![]() 内的方程组,我们对矩阵 A 模 p 求逆,公式
内的方程组,我们对矩阵 A 模 p 求逆,公式 ![]() (其中,
(其中,![]() (定理1.6.9))对整数矩阵是有效的,因此,矩阵的列值被它们的同余类替换之后,在
(定理1.6.9))对整数矩阵是有效的,因此,矩阵的列值被它们的同余类替换之后,在 ![]() 中仍然成立。若δ 的同余类不为零,同我们可以通过计算
中仍然成立。若δ 的同余类不为零,同我们可以通过计算 ![]() 求得
求得 ![]() 中A的逆矩阵。
中A的逆矩阵。
推论 3.2.8 令 AX = B 为一个有 n 个未知数的n 阶线性方程组,其中,A 和B 的列值在 ![]() 中,并令 δ = det A 。如果 δ 不为零,则这个方程组在
中,并令 δ = det A 。如果 δ 不为零,则这个方程组在 ![]() 中具有唯一解。
中具有唯一解。
例如,考虑方程组 AX = B ,其中
方程组的系数是整数,因此,AX = B 在 ![]() 中对任意素数 p 定义了一个方程组。A的行列式是 42 ,因此,方程组在
中对任意素数 p 定义了一个方程组。A的行列式是 42 ,因此,方程组在 ![]() 中对于任意不能整除42的p (即,所有不同于2,3,和 7的p )具有唯一解。例如,当计算模13的时候,det A = 3 。因为在
中对于任意不能整除42的p (即,所有不同于2,3,和 7的p )具有唯一解。例如,当计算模13的时候,det A = 3 。因为在 ![]() 中
中 ![]() ,
,
(译注:以上疑似有误,应该是
这个方程组在 ![]() 和
和 ![]() 中没有解。碰巧在
中没有解。碰巧在 ![]() 中有解,尽管
中有解,尽管 ![]() 。
。
具有列值在素数域 ![]() 中的可逆矩阵提供了有限群的新示例,即有限域上的一般线性群:
中的可逆矩阵提供了有限群的新示例,即有限域上的一般线性群:
![]() {具有列值在素数域
{具有列值在素数域 ![]() 中的可逆矩阵n × n},
中的可逆矩阵n × n},
![]() {具有列值在素数域
{具有列值在素数域 ![]() 中且具有行列式1的可逆矩阵n × n}。
中且具有行列式1的可逆矩阵n × n}。
例如,列值位于 ![]() 中的可逆 2 × 2 群含有6个元素:
中的可逆 2 × 2 群含有6个元素:
(3.2.9) 。
这个群与对称群众 ![]() 是同构的。以上矩阵元素的列出阶序与
是同构的。以上矩阵元素的列出阶序与 ![]() 的元素的常规列表
的元素的常规列表 ![]() 一致。
一致。
素数域 ![]() 的一个将其与 ℂ的子域区分开来的属性是,循环将1加到其自身达一定的次数(事实上是p次)之后,就给出了 0 的结果。作为加法群
的一个将其与 ℂ的子域区分开来的属性是,循环将1加到其自身达一定的次数(事实上是p次)之后,就给出了 0 的结果。作为加法群 ![]() 的一个元素,一个域F 的特征(characteristic)便是1 的阶数(假设阶数有限)。它是使得 1 的 m 个副本的总和 1 + ... + 1 的计算结果为零的最小的正整数。若1的阶数是有无限的,即,1 + ... + 1 在
的一个元素,一个域F 的特征(characteristic)便是1 的阶数(假设阶数有限)。它是使得 1 的 m 个副本的总和 1 + ... + 1 的计算结果为零的最小的正整数。若1的阶数是有无限的,即,1 + ... + 1 在 ![]() 永不为0 ,则称这个域具有特征0 (characteristic zero),这在某种程度上似乎有悖常理。因此,ℂ 的子域有特征 0,而素域
永不为0 ,则称这个域具有特征0 (characteristic zero),这在某种程度上似乎有悖常理。因此,ℂ 的子域有特征 0,而素域 ![]() 有特征 p。
有特征 p。
引理 3.2.10 任意域 F 的特征要么是0,要么是一个素数。
证明:
为了避免引起混淆,我们分别令 ![]() 和
和 ![]() 来表示域 F 中的加法玄元和乘法玄元 。且若 k 是一个个正整数,我们令
来表示域 F 中的加法玄元和乘法玄元 。且若 k 是一个个正整数,我们令 ![]() 为
为 ![]() 复制 k 次后相加的和。假设特征 m 不为 0。则
复制 k 次后相加的和。假设特征 m 不为 0。则 ![]() 产生一个
产生一个 ![]() 的 m 阶循环子群H,且
的 m 阶循环子群H,且 ![]() 。则由
。则由 ![]() 产生的循环子群 H 的不同元素
产生的循环子群 H 的不同元素 ![]() ( k = 0,1,...,m - 1)(命题 2.4.2)。假设 m 不是素数,比如说,m = rs 且 1 < r ,s < m 。则
( k = 0,1,...,m - 1)(命题 2.4.2)。假设 m 不是素数,比如说,m = rs 且 1 < r ,s < m 。则 ![]() 和
和 ![]() 在乘法群
在乘法群 ![]() 中,但是,乘积
中,但是,乘积 ![]() (等于
(等于 ![]() ) 不在
) 不在 ![]() 中。这与
中。这与 ![]() 是群的事实相矛盾。
是群的事实相矛盾。
素域 ![]() 还具有另一个显著的属性:
还具有另一个显著的属性:
定理 3.2.11 乘法群的结构:令 p 为素数。则素域的乘法群 ![]() 是一个 p – 1 阶的乘法群。
是一个 p – 1 阶的乘法群。
我们将这个定理的证明推迟到第15章中进行,在那里,我们将证明每一个有限域的乘法群都是循环群(定理15.7.3)。
![]() 循环群
循环群 ![]() 的一个生成元(generator)被称为模p原根(primitive root)。
的一个生成元(generator)被称为模p原根(primitive root)。
存在两个模p原根,即,3 和 5,以及四个模11原根。去掉上划线,3 模 7 的原根的幂 ![]() ,
, ![]() ,
, ![]() ,... 按下列的次序列出了
,... 按下列的次序列出了 ![]() 的非零元素:
的非零元素:
(3.2.12) ![]() 。因此,有两种方式可以用于列出
。因此,有两种方式可以用于列出 ![]() 的非零元素,即,按加法和按乘法。若α 是模 p原根,则
的非零元素,即,按加法和按乘法。若α 是模 p原根,则
(3.2.13) ![]() 。
。
3.3 向量空间(VECTOR SPACES)
有了域的一些概念和例子之后,我们继续进行向量空间的定义。
定义 3.3.1 一个域F上的一个向量公间V是一个集合与两个随后所述的合成律的结合体。这两个合成律为:
(a) 加法:V × V ⟶ V ,对于 V 中的 v 和 w,记为 v ,w ⇝ v + w 。
(b) 按域的元素的标量乘:F × V ⟶ V ,对于 F 中的 c和 V 中的v ,记为 c ,v ⇝ cv 。
这两条合成律需满足下面的公理:
![]() 加法使得V 成为一个具有 0 作为玄元的交换群
加法使得V 成为一个具有 0 作为玄元的交换群 ![]() 。
。
![]() 对于V中的任意v ,有 1v = v 。
对于V中的任意v ,有 1v = v 。
![]() 结合律:对于 F 中的任意 a 和 b 以及 V中的任意v,有 (ab)v = a(bv)。
结合律:对于 F 中的任意 a 和 b 以及 V中的任意v,有 (ab)v = a(bv)。
![]() 分配律:对于 F 中的任意 a 和 b 以及 V中的任意v和 w,有 (a + b)v = av + bv 和 a(v + w) = av + aw 。
分配律:对于 F 中的任意 a 和 b 以及 V中的任意v和 w,有 (a + b)v = av + bv 和 a(v + w) = av + aw 。
当加法和标量乘如惯常定义(3.1.1)时,列值位于域 F 的列向量空间 ![]() 构成域F上的一个向量空间。
构成域F上的一个向量空间。
实向量空间(ℝ上的向量空间)的更多一些例子:
例子 3.3.2
(a) 令 V = ℂ 为复数集合。忽视关于两个复数的乘法。仅关注其两个复数的加法和一个复数α与一个实数 r 的标量乘法 rα 这两种运算。这两种运算使得 V 成为一个实向量空间。
(b) 实数多项式 ![]() 的集合是一个实数向量空间,以多项式加法和实数与多项式的标量乘法作为其合成律。
的集合是一个实数向量空间,以多项式加法和实数与多项式的标量乘法作为其合成律。
(c) 实数轴上连贯实数值函数的集合是一个实数向量空间,它以函数加法 f + g 和 实数与函数的乘法作为其合成律。
(d) 微分方程 ![]() 的解的集合构成一个向量空间。
的解的集合构成一个向量空间。
我们的每个例子都具有比我们将其视为向量空间时所看到的更多的结构,这是很典型的。 任何特定的例子都肯定具有与其他示例区分开来的额外功能,但这不是缺点。相反,抽象方法的优势在于公理的结果可以应用于许多不同的情况。
子空间和同构这两个重要的概念与子群和群的同构类似。与 ![]() 子空间一样,一个域 F上的一个向量空间V的一个子空间 W 在加法和标量乘的合成律之下是一个非空的闭合子集。对于一个子空间W,如果它既不是整个空间V,又不是零子空间 {0}, 则它是一个真子空间(proper subspace)。例如,微分方程(3.3.2)(d)的解的空间是实数轴上所有连续函数构成的空间的真子空间。
子空间一样,一个域 F上的一个向量空间V的一个子空间 W 在加法和标量乘的合成律之下是一个非空的闭合子集。对于一个子空间W,如果它既不是整个空间V,又不是零子空间 {0}, 则它是一个真子空间(proper subspace)。例如,微分方程(3.3.2)(d)的解的空间是实数轴上所有连续函数构成的空间的真子空间。
命题 3.3.3 令 ![]() 为列值位于域F的列向量向量空间。一个非零向量w的标量乘{cw}构成的V的每一个真子空间。不同的真子空间共有的向量仅为零向量。
为列值位于域F的列向量向量空间。一个非零向量w的标量乘{cw}构成的V的每一个真子空间。不同的真子空间共有的向量仅为零向量。
证明命题3.1.4的证明对这个命题的证明继续有效,不再赘述。
例子 3.3.4 令 F 为素域 ![]() 。空间
。空间 ![]() 包含
包含 ![]() 个向量,(
个向量,( ![]() ) 个向量非零。因为存在 p – 1 个非零标量,由一个非零向量 w 所张成的子空间 W = {cw} 将包含 p – 1 个非零向量。因此,
) 个向量非零。因为存在 p – 1 个非零标量,由一个非零向量 w 所张成的子空间 W = {cw} 将包含 p – 1 个非零向量。因此,![]() 包含
包含 ![]() 个真子集。
个真子集。
从一个向量空间V到另一个向量空间V’的一个同构φ(两个空间都基于同一个域F )是一个与两个合成律兼容双射映射 φ :V ⟶ V ’,即,对于V中的任意v 和 w 以及F中的任意c,这个双射使得
(3.3.5) φ(v + w) = φ(v) + φ(w) 和 φ(cv) = cφ(v)
成立。
例子 3.3.6
(a) 令 ![]() 表示列值位于域F 中的n × n 矩阵的集合。这个集合是域F上的一个向量空间,并且与长度为
表示列值位于域F 中的n × n 矩阵的集合。这个集合是域F上的一个向量空间,并且与长度为 ![]() 的列向量空间同构。
的列向量空间同构。
(b) 如果我们将复数集合视为一个实向量空间(译注:应理解为将复数的实部和虚部看成是实向量的两个分量),例如在 (3.3.2)(a)中,发送 ![]() 的映射
的映射 ![]() 是一个同构。
是一个同构。
3.4 (向量空间的)基底和维数(BASES AND DIMENSION)
我们讨论在向量空间中进行加法和标量乘法运算时使用的术语。涉及到的新概念有张成(span)、独立性(independence)和基底(basis)(译注:有的书上又使用“base”,可理解为以此为“基础”,或以此为“根基”,在不致引起混淆的情况下,简称为“基”,或“底”,因为在数学上,使用“基”作为术语的数学分支不只一个,比如,指数的底数和进制表示的底数也称为“基”或“底”)。
在这里,我们使用向量的有序集(ordered sets)。我们将无序集合放在大括号中,并用圆括号将有序集合括起来,以便清楚地区分。因此,有序集合(v, w) 与有序集合 (w, v) 不同,而无序集合 { v, w } 和 { w, v } 相等。有序集中允许重复。所以 (v, v, w) 是有序集合,它与 (v, w) 不同,与无序集合的约定相反,其中 { v, v, w } 和 { v, w } 表示同一个集合。
令 V 为一个域 F上的一个向量空间,并令 ![]() 为 V 的元素的一个有序集。则 S 的一个线性组合(linear combination)是一个形如
为 V 的元素的一个有序集。则 S 的一个线性组合(linear combination)是一个形如
(3.4.1) ![]() (其中,
(其中,![]() 在 S 中 )
在 S 中 )
的向量。
允许标量出现在向量的任一侧会很方便。我们简单地约定,如果v是向量而c 是标量,则符号 vc 和 cv 代表同一个向量,即通过标量乘法获得的向量。因此,![]() 。
。
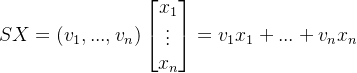
矩阵表示法提供了一种紧凑的方式来书写线性组合,并且我们在选择书写有序向量集的方式时考虑到了这一点。由于它的列值(entries)是向量,因此我们将数组 ![]() 称为超向量(hypervector)。向量空间的两个元素的乘法没有定义,但我们确实有标量乘法。这就允许我们将
称为超向量(hypervector)。向量空间的两个元素的乘法没有定义,但我们确实有标量乘法。这就允许我们将 ![]() 中的超向量 S 与一个列向量 X的乘积解释为矩阵乘法
中的超向量 S 与一个列向量 X的乘积解释为矩阵乘法
(3.4.2)
通过计算右边的标量乘再向量加,我们获得另一个向量—— 一个标量系数在右的线性组合。
我们取这个线性方程组的解的 ![]() 的子空间W
的子空间W
(3.4.3) ![]() 或 AX = 0 ,其中 A = (2,-1,-2)
或 AX = 0 ,其中 A = (2,-1,-2)
作为例子。方便的两个特解 ![]() 和
和 ![]() 及其一个线性组合
及其一个线性组合 ![]() 如下所示:
如下所示:
(3.4.4)
若我们写成 ![]() 且
且 ![]() 如 (3.4.4)的记法,并且
如 (3.4.4)的记法,并且 ![]() ,则这个线性组合可以按矩阵形式记为 SY。
,则这个线性组合可以按矩阵形式记为 SY。
![]() 由向量
由向量 ![]() 的所有线性组合构成的向量集合构成V的一个子空间,称其为由集合张成的子空间。
的所有线性组合构成的向量集合构成V的一个子空间,称其为由集合张成的子空间。
正如3.1节所述,这个张成的子空间是V的含有S的最小子空间,通常记为 Span S。 一个单一的向量 ![]() 张成的子空间是
张成的子空间是 ![]() 的标量乘
的标量乘 ![]() 构成的空间。
构成的空间。
人们也可以针对一个向量无限集定义张成空间,我们将在3.7节讨论这个问题。现在我先假设集合是有限集。
引理 3.4.5 令 S 为V 向量的一个有序集,并令W 为V 的一个子空间。若 S ⊂ W ,则有 Span S ⊂ W (译注:如上所述,读作“这个张成的子空间是V的含有S的最小子空间”)。
一个列值在F 中的 m ×n 矩阵的列向量空间(column space)是由矩阵的列所张成的空间 ![]() 的子空间。对此有一个重要的解释:
的子空间。对此有一个重要的解释:
命题 3.4.6 令 A 为一个m×n 矩阵,并令 B 为一个列向量,且两者列值都在域 F 中。则对于方程组 AX = B ,当且仅当 B 在 A 的列向量空间中时,其具有一个位于 ![]() 的 X 的解。
的 X 的解。
证明:
令 ![]() ,...,
,...,![]() 表示 A 的列。对于任意列向量
表示 A 的列。对于任意列向量 ![]() ,矩阵的积 AX 是列向量
,矩阵的积 AX 是列向量 ![]() 。这是列值(列向量空间的元素)的一个线性组合,并且若 AX = B ,则 B 便是这个线性组合。
。这是列值(列向量空间的元素)的一个线性组合,并且若 AX = B ,则 B 便是这个线性组合。
向量 ![]() ,...,
,...,![]() 之间的一个线性关系(linear relation)是计算结果为0的任意线性组合——即,形如
之间的一个线性关系(linear relation)是计算结果为0的任意线性组合——即,形如
( 3.4.7 ) ![]()
的在V中成立的任意方程,其中,系数 ![]() 在域 F 中。线性组合很有用,因为,若
在域 F 中。线性组合很有用,因为,若 ![]() 不等于0,则方程 ( 3.4.7 ) 可以对
不等于0,则方程 ( 3.4.7 ) 可以对 ![]() 求解。
求解。
定义 3.4.8 对于向量 ![]() 的一个有序集,若除了平凡的(trivial)(译注:即显而易见的)线性组合( X = 0这种情况,即,在其中,所有系数
的一个有序集,若除了平凡的(trivial)(译注:即显而易见的)线性组合( X = 0这种情况,即,在其中,所有系数 ![]() 都是0),不存在线性组合 SX = 0,则称这个有序集是独立的(independent),或者线性独立的(linearly independent)。不是线性独立的集合则是线性相关的(dependent)。(译注:线性独立性即线性无关性,集合之间没有共同部分,没有相似部分;相反,相关性即有相似性,一个集合可以用另一个相关性的集合线性表示。)
都是0),不存在线性组合 SX = 0,则称这个有序集是独立的(independent),或者线性独立的(linearly independent)。不是线性独立的集合则是线性相关的(dependent)。(译注:线性独立性即线性无关性,集合之间没有共同部分,没有相似部分;相反,相关性即有相似性,一个集合可以用另一个相关性的集合线性表示。)
一个独立的集合S 不能有任何重复向量。若S 的两个向量 ![]() 和
和 ![]() 是相等的,则
是相等的,则 ![]() 量是形如( 3.4.7 )的一个线性关系,其它的系数均为0。此外,在一个独立的集合中,向量
量是形如( 3.4.7 )的一个线性关系,其它的系数均为0。此外,在一个独立的集合中,向量 ![]() 没有等于0 的。因为,若
没有等于0 的。因为,若 ![]() 是0 ,则
是0 ,则 ![]() 是一个线性关系。
是一个线性关系。
引理 3.4.9
(a) 对于一个向量构成的集合 ![]() ,当且仅当
,当且仅当 ![]() 时,其是独立的。
时,其是独立的。
(b) 对于两个向量构成的集合 ![]() ,若任一向量都不是对方的倍数,则这两向量是相互独立的。
,若任一向量都不是对方的倍数,则这两向量是相互独立的。
(c) 一个独立集合的任意重排序仍是独立的。
假设 V 是空间 ![]() ,并且我们已知集合
,并且我们已知集合 ![]() 中的向量的坐标向量。则方程 SX = 0 给了我们一个含有n 个未知数
中的向量的坐标向量。则方程 SX = 0 给了我们一个含有n 个未知数 ![]() 的m 个齐次(homogeneous)线性方程构成的方程组,并且我们可以通过解这个方程组来确定其方程之间的独立性。
的m 个齐次(homogeneous)线性方程构成的方程组,并且我们可以通过解这个方程组来确定其方程之间的独立性。
例子 3.4.10 令 ![]() 为
为 ![]() 中的向量集,且其坐标向量分别是
中的向量集,且其坐标向量分别是
(3.4.11)
令 A 表示由这些列向量构成的矩阵:
(3.4.12)
则一个线性组合将具有形式为 ![]() ,并且其坐标向量为
,并且其坐标向量为 ![]() 。齐次方程 AX = 0 具有非平凡解(译注:即非零解,非显而易见的解,需要费一定周折才能求得的解),因为它是含有4个未知数的三个齐次方程组。因此,集合S是独立的。在另一方面,由矩阵(3.4.12)前三列所构成的 3×3 矩阵 A’的行列式等于1,因此方程 A’ X = 0 仅有平凡解。因此,
。齐次方程 AX = 0 具有非平凡解(译注:即非零解,非显而易见的解,需要费一定周折才能求得的解),因为它是含有4个未知数的三个齐次方程组。因此,集合S是独立的。在另一方面,由矩阵(3.4.12)前三列所构成的 3×3 矩阵 A’的行列式等于1,因此方程 A’ X = 0 仅有平凡解。因此,![]() 是一个独立集合。
是一个独立集合。
定义 3.4.13 一个向量空间V 的一个基(basis)是一个线性无关且也张成向量空间V 的向量的集合 ![]() 。
。
我们通常使用粗体符号(例如 B )来表示一个基。按以上定义的集合 ![]() 是
是 ![]() 的一个基,因为方程 A’ X = 0 对于所有的B都具有唯一解(见1.2.21)。按(3.4.4)定义的集合
的一个基,因为方程 A’ X = 0 对于所有的B都具有唯一解(见1.2.21)。按(3.4.4)定义的集合 ![]() 是方程
是方程 ![]() 的解空间的一个基,尽管我们还没有验证它。
的解空间的一个基,尽管我们还没有验证它。
命题 3.4.14 对于集合 ![]() 以及向量空间V ,当且仅当V 中的每一个向量 w 都可以按唯一的方式写成一个线性组合
以及向量空间V ,当且仅当V 中的每一个向量 w 都可以按唯一的方式写成一个线性组合 ![]() 的时候,这个向量 B 是V的一个基。
的时候,这个向量 B 是V的一个基。
证明:
称零向量仅可以按一种方式写成一个线性组,按照这种表述,可以重述独立性的定义。如果每一个向量都可以唯一地写成一个线性组合,则 B 是独立的,并张成 V ,因此,它是一个基(basis)。反之,假如 B 是一个基。则 V 中的每一个向量 w,都可以写成 B 的一个线性组合。假设 w 按两种方式写为线性组合,比如 w = BX = BX’。令 Y = X – X’,则 BY = 0 ,这是向量 ![]() ,...,
,...,![]() 之间一个线性组合,这些向量是独立的 。因此,X – X’= 0 , 这说明这两个线性组合是相同的。
之间一个线性组合,这些向量是独立的 。因此,X – X’= 0 , 这说明这两个线性组合是相同的。
令 ![]() 为列向量空间。如前一样,用
为列向量空间。如前一样,用 ![]() 表示第i个位置为1而其它位置为0的列向量(见(1.1.24))。集合
表示第i个位置为1而其它位置为0的列向量(见(1.1.24))。集合 ![]() 是
是 ![]() 的一个基,称其为标准基(standard basis)。若
的一个基,称其为标准基(standard basis)。若 ![]() 中一个向量的坐标向量是
中一个向量的坐标向量是 ![]() ,则根据标准基,
,则根据标准基, ![]() 是v的唯一表达式。
是v的唯一表达式。
我们现在讨论与张成(span)、独立性(independence)和基(basis)这三个概念相关的主要事实。最重要的事实是定理 3.4.18。
命题 3.4.15 令 ![]() 为向量的一个有序集,令 w 为 V 中的任意向量,并令 S’ = (S ,w ) 为通过将w 加到S 所获得的集合。
为向量的一个有序集,令 w 为 V 中的任意向量,并令 S’ = (S ,w ) 为通过将w 加到S 所获得的集合。
(a) 当且仅当 w 在 Span S 中时,Span S = Span S’ 。
(b) 假设 S 是独立的。则当且仅当w 不在 Span S 中时,S’ 是独立的。
证明:
这个内容非常基础,因此我们略去大部分的证明。我们仅证明若 S 是独立的而 S’ 不是独立的,则 w 在 Span S 中这种情况。若 S’ 是独立的,则存在某种线性关系
![]() ,
,
其中,系数 ![]() ,...,
,...,![]() 和 y 不全为0 。若系数 y是0,则表达式缩减为 SX = 0 ,且因为假设 S 是独立的,我们也可以推断出 X = 0 ,这关系是平凡的,这与我们的假设是矛盾的。因此 y ≠ 0 ,则我们可以针对 w 求得
和 y 不全为0 。若系数 y是0,则表达式缩减为 SX = 0 ,且因为假设 S 是独立的,我们也可以推断出 X = 0 ,这关系是平凡的,这与我们的假设是矛盾的。因此 y ≠ 0 ,则我们可以针对 w 求得 ![]() ,...,
,...,![]() 的一个线性组合。
的一个线性组合。
![]() 对于一个线性空间V,若其可由某些有限向量张成,则称其是有限维的(finite-dimensional)。否则,称V是无限维的(infinite-dimensional)。
对于一个线性空间V,若其可由某些有限向量张成,则称其是有限维的(finite-dimensional)。否则,称V是无限维的(infinite-dimensional)。
在本节余下的部分,我们的向量都是有限维的。
命题 3.4.16 令V 为有限维向量空间。
(a) 令S为张成V 的有限子集,并令 L为 V 的一个独立子集。通过将S的元素加到 L 的方式,可以获得V 的一个基。
(b) 令S 为张成V 的有限子集。通过从S 中删去元素的方式,可以获得V 的一个基。
证明:
(a) 若 S 包含于 Span L 中,则L张成V,因此,它是一个基(3.4.5)。否则,我们先择S中的一个不在Span L 中的元素v 。根据命题 3.4.15 ,L’ = (L,v)是独立的。我们用L替换 L’。因为S是有限的,通常我们仅对有限维的情况可以这样做。因此,最终我们获得一个基。
(b) 假如S是独立的,则存在一个线性关系 ![]() , 其中,某些系数(比如说
, 其中,某些系数(比如说 ![]() ) 不为0。我们可以针对
) 不为0。我们可以针对 ![]() 解这个方程,这就证明了
解这个方程,这就证明了 ![]() 在由前面 (n - 1)个向量的集合
在由前面 (n - 1)个向量的集合 ![]() 所张成的空间中。继续按这种方式进行下去,最后我们会获得一族独立且仍旧张成空间V 的一族基。
所张成的空间中。继续按这种方式进行下去,最后我们会获得一族独立且仍旧张成空间V 的一族基。
注意:按这个推理,当V是零向量空间{0}的时候,会存在一个问题。以V中向量的任一个集合S开始,所有向量都等于0,我们的处理例程将一次扔掉一个向量,直到只有一个向量 ![]() 留下。而又因为
留下。而又因为 ![]() 是0,集合
是0,集合 ![]() 是相关的。我们如何进行下去呢?零空间并不是特别有趣,但它可能潜伏(lurk)在角落里,随时准备绊倒我们(trip us up)。我们必须考虑到在某些计算(例如求解齐次线性方程组)过程中出现的向量空间为零空间的可能性,尽管我们没有意识到这一点。为了避免将这种可能性作为特殊情况提及,我们采用以下定义:
是相关的。我们如何进行下去呢?零空间并不是特别有趣,但它可能潜伏(lurk)在角落里,随时准备绊倒我们(trip us up)。我们必须考虑到在某些计算(例如求解齐次线性方程组)过程中出现的向量空间为零空间的可能性,尽管我们没有意识到这一点。为了避免将这种可能性作为特殊情况提及,我们采用以下定义:
(3.4.17)
![]() 空集合是独立的。
空集合是独立的。
![]() 空集合张成的空间是零空间{0} 。
空集合张成的空间是零空间{0} 。
根据这个定义,则空集是零向量空间的一个基。这些定义允许我们扔掉最后一个向量 ![]() ,这样,就挽救了以上这种证明方法。
,这样,就挽救了以上这种证明方法。
现在,我们触及到了关于独立性的主要事实:
定理 3.4.18 令 S 和 L 为一个向量空间V的有限子集。假设S 张成V 且L 是独立的。则S 至少包含与 L 一样多的元素:| S | ≥ | L |。
如前一样,| S |表示阶,即,集合 S 的元素个数。
证明:
假设 ![]() 和
和 ![]() 。我们假设 |S|<|L| ,即,m < n,我们证明 L是独立的。为了实现这一点,我们证明存在一个线性关系
。我们假设 |S|<|L| ,即,m < n,我们证明 L是独立的。为了实现这一点,我们证明存在一个线性关系 ![]() ,其中,系数
,其中,系数 ![]() 不全为0。我们将这个不确定的关系记为 LX = 0。
不全为0。我们将这个不确定的关系记为 LX = 0。
因为 S 张成 V ,L的每一个元素 ![]() 都是S的一个线性组合,比如说
都是S的一个线性组合,比如说 ![]() ,其中,
,其中,![]() 是系数的列向量。我们将这些列向量组成一个 m × n 矩阵
是系数的列向量。我们将这些列向量组成一个 m × n 矩阵
(3.4.19)
![]() 。
。
则
(3.4.20) ![]() 。
。
我们在未确定的线性组合中用SA替换L:
LX = (SA)X 。
标量乘的结合律意味着 (SA)X = S(AX )。这个证明与标题矩阵乘法的结合律的证明一样(我们略去)。若 AX = 0 ,则我们的线性组合 LX 也将为0。现在,因为 A 是一个 m×n ( m < n )矩阵,这个齐次方程组具有非平凡解 X 。则 LX = 0 正是我们所求的线性关系。
命题 3.4.21 令V 为一个有限维向量空间。
(a) V 的任意两个基(bases)(译注:basis的复数bases)具有相同的阶(相同的元素数目)。
(b) 令 B为一个基。若一个有限向量集S 张成 V,则当且仅当S是一个基的时候, |S | ≥ |B| 。
(c) 令 B为一个基。若一个向量集是独立的,则 | L| ≤ |B| ,且当且仅当 L是一个基的时候,| L | = |B| 。
证明:
(a) 在这里,我们指出,两个有限基 ![]() 和
和 ![]() 具有相同的阶,在推论3.7.7中我们将证明一个有限维向量空间的任一个基都是有限维的。在定理3.4.18中取
具有相同的阶,在推论3.7.7中我们将证明一个有限维向量空间的任一个基都是有限维的。在定理3.4.18中取 ![]() 和
和 ![]() 即可证明
即可证明 ![]() ,类似地,有
,类似地,有 ![]() 。
。
(b)和(c)部分可从(a)和命题3.4.16推断。
定义 3.4.22 一个有限维向量空间的维数是其一个基中的向量的数目。 维数将记为 div V 。
列向量空间 ![]() 的维数是n,因为标准基
的维数是n,因为标准基 ![]() 含有n 个元素。
含有n 个元素。
命题 3.4.23 若 W 是一个有限维向量空间 V 的一个子空间,则 W 是有限维的,且 div W ≤ div V 。此外,当且仅当 W = V 时,有 div W = div V 。
证明:
我们以W中任意独立的向量集 L开始,有可能是空集。若L不张成 W ,我们选取在 W中但不在L的张成空间的一个向量w 。则 L’= (L , w)将是独立的(3.4.15)。我们用 L’替换L 。
现在,很明显的是,若 L是W的一个独立子集,则将其视为 V 的一个独立子集时,它也是独立的。因此,定理 3.4.18 告诉我们 | L|≤ dim V。因此,将元素加入到 L的这个过程必须会有结束的时候,且当它结束的时候,我们将得到W的一个基。因为L包含最多 dim V 个元素,因此,div W ≤ div V 。因为 | L| = div V ,则命题 3.4.21 (c)证明 L 是 V 的一个基,因此,W = V 。
3.5 用基进行计算(COMPUTING WITH BASES)
基数目的是提供一种计算方法,我们在本节中学习如何使用它们。 我们考虑两个主题:如何根据基表达向量,以及如何将同一向量空间的不同基关联起来。
假设给到我们一个域F上的一个向量空间V 的一个基 ![]() 。记住:这意味着在向量空间V 中的每一个向量都可以恰好按一种方式(3.4.14)被表述为一个线性组合
。记住:这意味着在向量空间V 中的每一个向量都可以恰好按一种方式(3.4.14)被表述为一个线性组合
(3.5.1) ![]() (
( ![]() 在域 F 中 )。
在域 F 中 )。
标量 ![]() 是向量 v 关于基B的坐标(coordinates),而列向量
是向量 v 关于基B的坐标(coordinates),而列向量
(3.5.2)
是向量 v 关于基B的坐标向量(coordinate vector)(译注:即向量在基上的各个分量)。
例如,(cos(t),sin(t))是微分方程 y’’ = -y 的解空间的一个基。这个方程的每一个解都是这个基的一个线性组合。若给到我们另一个解f (t),则 f (t) 的坐标向量 ![]() 是使得
是使得 ![]() 成立的向量。显然,为了求得 X ,我们需要知道 f 的某些东西。不需要太多:只要确定两个系数足可。f 的大部分属性隐含于其作为这个微分方程的解这个事实中的。
成立的向量。显然,为了求得 X ,我们需要知道 f 的某些东西。不需要太多:只要确定两个系数足可。f 的大部分属性隐含于其作为这个微分方程的解这个事实中的。
如果已知一个维数为 n 的向量空间的一个基B,我们总是可以定义一个从空间 ![]() 到 V 的向量空间同构(isomorphism of vector spaces)(见3.3.5):
到 V 的向量空间同构(isomorphism of vector spaces)(见3.3.5):
(3.5.3) ![]() ,
,
这个同构发送 X ⇝ BX 。我们通用B表示这个同构,因为它发送了一个向量X 到 BX。
命题 3.5.4 令 ![]() 为一个向量空间V 的一个子集,并令
为一个向量空间V 的一个子集,并令 ![]() 为由
为由 ![]() 所定义的映射。则
所定义的映射。则
(a) 当且仅当S是独立的时候,ψ是单射的(injective),
(b) 当且仅当S是张成V的时候,ψ是满射的(surjective),和
(c) 当且仅当S是V的一个基的时候,ψ是双射的(bijective)。
以上可以从独立,张成,和基的定义推导出。
已知一个基,可通过对映射ψ (3.5.3)求逆的方式获得V中一个向量v的坐标向量。除非明确地给出一个基,否则我们没有求逆函数的公式,但是同构的存在性是有趣的:
推论 3.5.5 一个域 F 上的每一个n维向量空间V 都与列向量空间 ![]() 同构。
同构。
另请注意,当 m ≠ n的时候,![]() 与
与 ![]() 不同构,因为
不同构,因为 ![]() 具有n个元素的基,而基的元素的数目仅取决于向量空间。因此,一个域 F上的有限维向量空间完全是被分类的。列向量空间
具有n个元素的基,而基的元素的数目仅取决于向量空间。因此,一个域 F上的有限维向量空间完全是被分类的。列向量空间 ![]() 是同构类的代表元素。
是同构类的代表元素。
一旦选定了一个基,一个n 维列向量空间与 ![]() 是同构的这个事实允许我们将向量空间上的问题转换到熟悉的列向量代数问题。 遗憾的是,同一向量空间V具有很多不同的基。当持有一个自然基的时候,将向量空间V 与一个同构空间
是同构的这个事实允许我们将向量空间上的问题转换到熟悉的列向量代数问题。 遗憾的是,同一向量空间V具有很多不同的基。当持有一个自然基的时候,将向量空间V 与一个同构空间 ![]() 关联起来是十分有用的。在这种情况下,我们必需选择坐标,即,必需变换基。
关联起来是十分有用的。在这种情况下,我们必需选择坐标,即,必需变换基。
例如,一个齐次线性方程 AX = 0 的解空间几乎从不会有自然基。方程 ![]() 的解空间 W 维数是2,此前我们列出过一个基:
的解空间 W 维数是2,此前我们列出过一个基: ![]() , 其中,
, 其中,![]() ,
,![]() (见 (3.4.4))。使用这个基,我们获得了一个向量空间同构
(见 (3.4.4))。使用这个基,我们获得了一个向量空间同构 ![]() ,我们可以使用B 来表示。因为方程中的未知数标为
,我们可以使用B 来表示。因为方程中的未知数标为 ![]() ,在这里,我们必须为
,在这里,我们必须为 ![]() 的变元选择另一个符号。我们将使用
的变元选择另一个符号。我们将使用 ![]() 。这个同构B 将Y 发送到
。这个同构B 将Y 发送到 ![]() ,如(3.4.4)所示。
,如(3.4.4)所示。
然而,这两个特解 ![]() 和
和 ![]() 并没什么特别之处。大部分其它的解对(pairs)同样契合良好。解
并没什么特别之处。大部分其它的解对(pairs)同样契合良好。解 ![]() 和
和 ![]() 给到了我们 W 的第二个基
给到了我们 W 的第二个基 ![]() 。以上任一基都足以唯一地描述方程的解空间。方程的一个解可以写成以下任一形式
。以上任一基都足以唯一地描述方程的解空间。方程的一个解可以写成以下任一形式
(3.5.6)
3.5.1 换基(Change Of Basis)
假设给到我们同一个向量空间V的两个基,比如,![]() 和
和 ![]() 。我们希望执行两个计算。首先,我们要问:这两个基之间是怎样的关系?第二,V中的一个向量v 针对这些基中的第一个基都有一个坐标向量。因此,我们要问:这两个坐标向量之间是怎样的关系?这些是有关换基的计算,并且它们在此后的章节中也十分重要。如果你不存细地组织好这些符号,它们可以令你发疯。
。我们希望执行两个计算。首先,我们要问:这两个基之间是怎样的关系?第二,V中的一个向量v 针对这些基中的第一个基都有一个坐标向量。因此,我们要问:这两个坐标向量之间是怎样的关系?这些是有关换基的计算,并且它们在此后的章节中也十分重要。如果你不存细地组织好这些符号,它们可以令你发疯。
我们姑且将B视为旧的基,而将B’ 视为新的基。我们注意到,新的基B’ 的每一个向量都是旧的基的一个线性组合。我们将这个线性组合写为
(3.5.7) ![]() 。
。
当使用旧的基向量进行计算的时候,列向量 ![]() 是新的基向量
是新的基向量 ![]() 的坐标向量。我们将这些列向量聚成一个方阵P,获得了一个矩阵方程 B’ = B P :
的坐标向量。我们将这些列向量聚成一个方阵P,获得了一个矩阵方程 B’ = B P :
(3.5.8)
这个矩阵是 P 换基矩阵(basechange matrix)(注:这个换基矩阵是在第一版中使用的矩阵的逆矩阵)。
命题 3.5.9
(a) 令 B和 B’ 为一个向量空间V的两个基,换基矩阵 P 是由两个基B和 B’ 唯一地确定的一个可逆矩阵。
(b) 令 ![]() 为一个向量空间V的一个基,另外的基是形如 B’ = B P 的集合,其中 P 可以是任意可逆的 n ×n 矩阵。
为一个向量空间V的一个基,另外的基是形如 B’ = B P 的集合,其中 P 可以是任意可逆的 n ×n 矩阵。
证明:
(a) 方程 B’ = B P 将基向量 ![]() 描述为基 B 的一个线性组合。公有一种方式描述这个线性组合(3.4.14),因此,P是唯一的。为了证明P是可逆矩阵,我们交换B和B’的角色。存一个矩阵 Q 使得 B = B’ Q 。则 B = B’ Q = B P Q ,或者
描述为基 B 的一个线性组合。公有一种方式描述这个线性组合(3.4.14),因此,P是唯一的。为了证明P是可逆矩阵,我们交换B和B’的角色。存一个矩阵 Q 使得 B = B’ Q 。则 B = B’ Q = B P Q ,或者
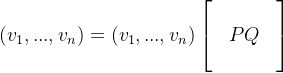 。这个方程将每个
。这个方程将每个 ![]() 描述为向量
描述为向量![]() 的一个线性组合。这个乘法矩阵 P Q 的列值是系数。但是,因为B是一个基,仅有一种方式将
的一个线性组合。这个乘法矩阵 P Q 的列值是系数。但是,因为B是一个基,仅有一种方式将 ![]() 表述为 向量
表述为 向量 ![]() 的一个线性组合,即,
的一个线性组合,即, ![]() ,或者,按矩阵记法,B = B I 。因此,P Q = I 。
,或者,按矩阵记法,B = B I 。因此,P Q = I 。
(b) 我们必须证明若 B 是一个基,且若P是一个可逆矩阵,则 B’ = B P 也是一个基。因为P是一个可逆矩阵,则 ![]() 。这表明,向量
。这表明,向量 ![]() 在基B’ 所张成的空间中,因此,B’ 张成V,又因为它具有与 B 同样多的元素数目,因此,它是一个基。
在基B’ 所张成的空间中,因此,B’ 张成V,又因为它具有与 B 同样多的元素数目,因此,它是一个基。
令 X 和 X ’ 为同一任意向量 v 分别针对两个基进行计算得到的坐标向量,即,v = BX 和 v = B X ’ 。使用替换 ![]() 便给到我们矩阵方程
便给到我们矩阵方程
(3.5.10) ![]() 。
。
这就证明了v 针对新的基 B’ 的坐标向量是 ![]() ,我们称为 X ’ 。
,我们称为 X ’ 。
概言之,我们有一个单一矩阵 P (即换基矩阵),具有双重属性
(3.5.11) B’ = B P 和 P X ’ = X ,
其中,X 和 X ’ 表示同一任意向量 v 针对两个基的坐标向量。这两个属性的每一个都刻画了 P 。请注意P 在这两种关系中的位置。
再次回到方程 ![]() ,令 B和 B’ 为如上所描述的(3.5.6)解空间W 的基。换基矩阵求解方程
,令 B和 B’ 为如上所描述的(3.5.6)解空间W 的基。换基矩阵求解方程
已经向量 v 针对两个基的坐标向量Y 和 Y ’ (在(3.5.6)中出现过)是按方程
另一个例子:令 B = (cos(t),sin(t)) 为微分方程 ![]() 的解空间的一个基。若我们允许复数值函数,则指数函数
的解空间的一个基。若我们允许复数值函数,则指数函数 ![]() 也是一个解,并且,
也是一个解,并且,![]() 是解空间的一个新的基。这个换基计算是
是解空间的一个新的基。这个换基计算是
换基矩阵容易确定的一种情况是,V 是列向量空间 ![]() ,则旧基是标准基
,则旧基是标准基 ![]() ,而新的基可以是任意的,我们仍用
,而新的基可以是任意的,我们仍用 ![]() 表示。令
表示。令 ![]() 针对标准基的坐标向量是列向量
针对标准基的坐标向量是列向量 ![]() 。因此,
。因此, ![]() 。我们将这些列向量组装成一个n×n 矩阵并用[B]表示:
。我们将这些列向量组装成一个n×n 矩阵并用[B]表示:
(3.5.13)
即,[B] = E[B] 。因此,[B] 是从标准基E 到 B的换基矩阵。
3.6 (子空间的)直和(DIRECT SUMS)
一个向量集的独立和张成的概念对子空间而言具有类似之处。若 ![]() , ... ,
, ... , ![]() 是一个向量空间V的子空间,则向量v 的集合可以写为和式
是一个向量空间V的子空间,则向量v 的集合可以写为和式
(3.6.1) ![]() ,
,
其中,![]() 在
在 ![]() 中,以上向量v的集合表达式被称为子空间的和(sum),或者子空间的张成(span),并使用记法
中,以上向量v的集合表达式被称为子空间的和(sum),或者子空间的张成(span),并使用记法 ![]() 来表示这个和:
来表示这个和:
(3.6.2) ![]() 且
且 ![]() 在
在 ![]() 中
中 ![]()
这个子空间的和是含有所有子空间 ![]() , ... ,
, ... ,![]() 的V 的最小子空间。它类似于向量的一个集合的张成。
的V 的最小子空间。它类似于向量的一个集合的张成。
对于子空间 ![]() ,... ,
,... , ![]() , 若不存在和
, 若不存在和 ![]() (
( ![]() 在
在 ![]() 中 ) , 则除开平凡和(对于所有i ,
中 ) , 则除开平凡和(对于所有i , ![]() )这种情况,称其为独立的。换句话说,若
)这种情况,称其为独立的。换句话说,若
(3.6.3) ![]() (
( ![]() 在
在 ![]() 中 ) ,
中 ) ,
意味着对每一个 i ,都有 ![]() ,则空间是独立的。
,则空间是独立的。
注意:假设 ![]() 是V 的元素,并令
是V 的元素,并令 ![]() 为向量
为向量 ![]() 的张成。则当且仅当集合
的张成。则当且仅当集合 ![]() 是独立的时候,子空间
是独立的时候,子空间 ![]() 是独立的。如果我们对比(3.4.8) 和 (3.6.3) ,这一点就变得显而易见。根据子空间的概念,这个表述事实上更为简洁,因为,在(3.6.3)中,标量系数不必置于向量
是独立的。如果我们对比(3.4.8) 和 (3.6.3) ,这一点就变得显而易见。根据子空间的概念,这个表述事实上更为简洁,因为,在(3.6.3)中,标量系数不必置于向量 ![]() 的前面。由于每个
的前面。由于每个 ![]() 在标量乘的定律下是闭合的,一个标量乘
在标量乘的定律下是闭合的,一个标量乘 ![]() 只不过是
只不过是 ![]() 的另一个元素而已。
的另一个元素而已。
我们忽略以下命题的证明。
命题 3.6.4 令 ![]() , ... ,
, ... ,![]() 是有限维向量空间V 的子空间,并令
是有限维向量空间V 的子空间,并令 ![]() 为
为 ![]() 的一个基 。
的一个基 。
(a) 下面的条件是等价的:
![]() 子空间
子空间 ![]() 是独立的,其和
是独立的,其和 ![]() 等于 V 。
等于 V 。
![]() 通过追加基
通过追加基 ![]() 所获得的集合
所获得的集合 ![]() 是V 的一个基。
是V 的一个基。
(b) ![]() ,当且仅当每个子空间 独立的时候,可取得等号。
,当且仅当每个子空间 独立的时候,可取得等号。
(c) 若对于 i = 1 ,.., k , ![]() 是
是 ![]() 的子空间,并且,若空间
的子空间,并且,若空间 ![]() 是独立的,则其子空间
是独立的,则其子空间 ![]() 也是独立的。
也是独立的。
若满足命题 3.6.4 (a) 的条件,则我们称 V 是子空间 ![]() 的直和(direct sum)(译注:即由所有独立的子空间构的和,且恰好等于整个向量空间V ),我们记为
的直和(direct sum)(译注:即由所有独立的子空间构的和,且恰好等于整个向量空间V ),我们记为 ![]() :
:
(3.6.5) 若 ![]() 且
且 ![]() 是独立的,则
是独立的,则
![]() 。
。
若 V 是各子空间的直和,则 V 中的每一个向量v 都可以恰好以一种方式写成(3.6.1)的形式。
命题 3.6.6 令 ![]() 和
和 ![]() 为一个有限维向量空间 V 的子空间。
为一个有限维向量空间 V 的子空间。
(a) ![]() 。
。
(b) 当且仅当 ![]() 时,
时, ![]() 和
和 ![]() 是独立的。
是独立的。
(c) 当且仅当 ![]() 且
且 ![]() 时,V 是直和
时,V 是直和 ![]() 。
。
(d) 若 ![]() ,则存在
,则存在 ![]() 一个的一个子空间
一个的一个子空间 ![]() ,使得
,使得 ![]() 。
。
证明:
我们证明关键部分(a):我们选取 ![]() 的一个基
的一个基 ![]() , 并将其扩展为
, 并将其扩展为 ![]() 的一个基
的一个基 ![]() 。我们也将
。我们也将![]() 扩展成
扩展成 ![]() 的一个基
的一个基 ![]() 。则
。则 ![]() ,
, ![]() 和
和 ![]() 。如果我们证明
。如果我们证明 ![]() 个元素的集合
个元素的集合 ![]() 是
是 ![]() 的一个基,这个论断将顺承。
的一个基,这个论断将顺承。
我们必须证明 (U , V , W ) 是独立的,并且张成 ![]() 。
。![]() 的一个元素具有形如
的一个元素具有形如 ![]() 的形式,其中,
的形式,其中,![]() 在
在 ![]() 中,而
中,而 ![]() 在
在 ![]() 中。根据
中。根据 ![]() 的基 U , V ),我们将
的基 U , V ),我们将 ![]() 写成诸如
写成诸如 ![]() 。我们与将
。我们与将 ![]() 写成
写成 ![]() 的基 (U , W )的一个线性组合
的基 (U , W )的一个线性组合 ![]() 。则
。则 ![]() 。
。
下一步,假设给到我们一个向量(U , V , W )元素之间的线性关系 UX + VY + WZ = 0 。我们将其写为 UX + VY = -WZ 。这个方程的左边在 ![]() 中,而方程的右边在
中,而方程的右边在 ![]() 中。因此,-WZ 在
中。因此,-WZ 在 ![]() 中,因此,它是基 U的线性组合 U X’ 。这给予我们一个方程 UX’ + WZ = 0 。因为集合 (U , W) 是
中,因此,它是基 U的线性组合 U X’ 。这给予我们一个方程 UX’ + WZ = 0 。因为集合 (U , W) 是 ![]() 的一个基,它是独立的,因此,X’ 和 Z 只能是 0 。这个已经关系就缩减为 UX + VY = 0 。但是,(U , V )也是一个独立集合。因此,X 和Y 是0 。这个关系是平凡的。
的一个基,它是独立的,因此,X’ 和 Z 只能是 0 。这个已经关系就缩减为 UX + VY = 0 。但是,(U , V )也是一个独立集合。因此,X 和Y 是0 。这个关系是平凡的。
3.7 无限维空间(INFINITE-DIMENSIONAL SPACES)
那种太大而不通过通有限向量集张成的空间被称为无限维向量空间(infinite-dimensional)。我们并不经常需要它们,但它们在分析中是非常重要的,因此,我们在此作简要讨论。
无限维向量空间最简单例子之一便是无限实行向量空间 ![]()
(3.7.1) ![]() 。
。
一个无限维向量可以视为一个实数序列 ![]() 。
。
空间 ![]() 具有许多无限维子空间。在此列举几个;读者也可以编造更多:
具有许多无限维子空间。在此列举几个;读者也可以编造更多:
例子 3.7.2
(a) 收敛序列:![]() 极限
极限 ![]() 存在
存在 ![]() 。
。
(c) 具有有限多项不同于0的项的序列。
![]() (对除了有限多n 的所有项)
(对除了有限多n 的所有项) ![]() 。
。
现在,假设V是一个有限维或无限维向量空间。一个向量无限集的“张成(span)”指的是什么呢?将一个值赋予一个无限的线性组合 ![]() 并非总是可能。若是向量空间
并非总是可能。若是向量空间 ![]() ,如果级数
,如果级数 ![]() 是收敛的,则可以赋予其一个值。但是很多级数不收敛,那么我们并不知道应该赋予什么值。在代数中,习惯于仅讨论有限多个向量的线性组合。一个无限集S的张成被定义为向量v 的集合,这些向量v 是有限多个S 的元素的线组合的:
是收敛的,则可以赋予其一个值。但是很多级数不收敛,那么我们并不知道应该赋予什么值。在代数中,习惯于仅讨论有限多个向量的线性组合。一个无限集S的张成被定义为向量v 的集合,这些向量v 是有限多个S 的元素的线组合的:
(3.7.3) ![]() (其中,
(其中,![]() 在 S 中)。
在 S 中)。
S 中的向量 ![]() 可以是任意的,允许数 r 依赖于向量v 并且可以任意大:
可以是任意的,允许数 r 依赖于向量v 并且可以任意大:
(3.7.4)
Span S = { S 的元素的有限线性组合}。
例如,令 ![]() 为
为 ![]() 中的行向量,且 1 作为其唯一非零坐标在第i个位置。令
中的行向量,且 1 作为其唯一非零坐标在第i个位置。令 ![]() 为这些向量的集合。这个集合不会张成
为这些向量的集合。这个集合不会张成 ![]() ,因为向量
,因为向量
![]()
不是一个(有限)线性组合。集合 E 的张成是子空间 Z (3.7.2)(c)。
对于一个有限或无限集 S ,若除了平凡关系(即,![]() ),不存在有限线性关系
),不存在有限线性关系
(3.7.5) ![]() (其中,
(其中, ![]() 在 S 中),
在 S 中),
则称集合 S 是独立的。此外,允许数 r 取任意值,即,对任意大的 r 和 S 的任意元素
![]() 这个条件都一定成立。例如,令
这个条件都一定成立。例如,令 ![]() ,若 w 和
,若 w 和 ![]() 是如上定义的元素,则其是独立的。根据独立性的这个定义,命题3.4.15 继续有效。
是如上定义的元素,则其是独立的。根据独立性的这个定义,命题3.4.15 继续有效。
与有限集一样,V 的一个基S 是张成 V 的一个独立集合。集合 ![]() 是空间 Z的一个基。单项式(monomials)
是空间 Z的一个基。单项式(monomials) ![]() 组成多项式空间(polynomials space)的一个基。使用 Zorn引理(Zorn’s lemma)和选择公理(Axiom o f Choice), 可以证明,每一个向量空间都有一个基(见附录,命题A.3.3)。然而,
组成多项式空间(polynomials space)的一个基。使用 Zorn引理(Zorn’s lemma)和选择公理(Axiom o f Choice), 可以证明,每一个向量空间都有一个基(见附录,命题A.3.3)。然而,![]() 的基有无数多个元素,并且不能说得非常准确。
的基有无数多个元素,并且不能说得非常准确。
让我们暂时回到向量空间 V 是有限维的情况(3.4.16),并询问是否可以有无限基。 我们在(3.4.21)中看到,任何两个有限基都有相同数量的元素。我们现在通过证明每个基都是有限的来完成这个图景。这是从下一个引理得出的。
引理 3.7.6 令V 为一个有限维向量空间,令S 为张成V 的任间集合。则 S 包含张成V 的有限子集。
证明: 假设,存在一个有限集,比如 ![]() ,它张成V。因为S张成V,所以,每个向量
,它张成V。因为S张成V,所以,每个向量 ![]() 都是S的有限多个元素的一个线性组合。我们用于将向量的所有元素写成线性组合的S的元素组成S的一个有限子集S ’ 。则这个向量
都是S的有限多个元素的一个线性组合。我们用于将向量的所有元素写成线性组合的S的元素组成S的一个有限子集S ’ 。则这个向量 ![]() 在 Span S ’ 中,又因为
在 Span S ’ 中,又因为 ![]() 张成V, 因此,S ’ 也张成V 。
张成V, 因此,S ’ 也张成V 。
推论 3.7.7 令V 为一个有限维向量空间。
![]() 每一个基都是有限的。
每一个基都是有限的。
![]() 张成V 的每一个集合S 都有一个基。
张成V 的每一个集合S 都有一个基。
![]() 每一个独立集合L是有限的,且可被扩展成一个基。
每一个独立集合L是有限的,且可被扩展成一个基。
I don't need to learn 8 + 7: I'll remember 8 + 8 and subtract 1.
(我不必学习 8 + 7: 我将记住 8 + 8 并减1 )
——T. Cuyler Young, Jr.
内容来源:
<
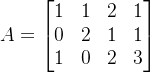
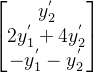
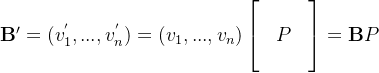
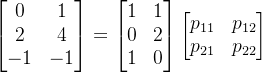
![[\mathbf{B}]= \begin{bmatrix} |&&|\\ B_{1}&\hdots&B_{n}\\ |&&| \end{bmatrix}](http://img.e-com-net.com/image/info8/47cd3667fd2d4ef38f27c23ba7ea4ffd.png)