08. 机器学习- 线性回归
文章目录
-
- 线性回归 LINEAR REGRESSION

从本次课程开始,大部分时候我将不再将打印结果贴出来了,因为太占用篇幅。小伙伴可以根据我的输出执行敲一遍代码来进行学习和验证。
同样是为了节省篇幅,我也不会再一行行那么仔细的解释代码了,一般只会告诉你我代码做了什么。其中的逻辑关系和关键词,小伙伴们自行好好的琢磨一下。
Hi, 你好。我是茶桁。
前几节课咱们主要是了解到了什么是人工智能,整个机器学习的工作路径等等。不过可以说,前面的几节课,从机器学习导论到上一节课介绍K-means,这些都还是一个铺垫。真正的内容,从这节课才算是正式开始。
咱们快速回顾一下,前几节课里的内容都有什么。之前咱们学习了什么是优化问题,然后还有什么是动态规划,什么是机器学习问题,以及监督学习和非监督学习的区别,我们还学习了一个非常著名的非监督学习方法:K-means。
从这一节课开始,我会给大家开始系统的学习监督学习,监督学习其实内容比较多,我们可能需要多花多一点时间。
在最开始,我还是要更大家强调一下上一节课上更大家讲的问题:要学习算法,不仅仅是要学习很多很多的这个算法模型,更重要的是什么要能够把问题抽象成一个一个的算法。工作场景中的问题并不能使用一个单独的算法模块能够解决。
机器学习算法只是人工智能其中的一个部分,或者说人工智能的某个部分,比方说取它的特征等等。它的某一个部分用在真正的工作中,用在项目中是很杂揉、很混合的一个状态。
咱们篇幅短内容多,密度比较大,短短几节课,可能是大家研究生课程一个月时间的内容。可以说,咱们课程还是有点难,信息量也比较大。
OK,开始第一个问题。
线性回归 LINEAR REGRESSION
咱们第一个要讲的,也是非常重要的一个方法,就是线性回归。
线性回归非常的简单,也非常的基础。但是它作为我们整个人工智能,整个深度学习中要讲的第一课,里面蕴含了非常多的机器学习的基本思想。所以大家一定要把它学清楚。如果能把它学好,其实对于咱们以后学习帮助非常大。
咱们来看一下,什么是线性回归。
在生活中有很多这样的问题,比方说咱们的血糖,往往在吃饭的时候,吃的糖分、碳水化合物等比较多,饭后的半个小时、一个小时内血糖会更高。
还有一种情况,抽烟抽的越多的人,得肺病的概率往往会越高。并不是一定说抽烟抽的多的人就一定会生病,但是抽烟抽的多的人得肺病的概率往往会越高。
那么还有一种情况,比方在咱们工作的时候,随着工作时间的增加,收入往往也会越来越多。尤其是在日本,是一个非常典型的情况。在日本基本上一个人的收入和他的工作年限是最相关的。他们在一个固定的时间内的薪资变化不会非常大。
比方说都是29岁、都是32岁、都是35岁,假如都在同一家公司,那么薪资待遇也会很接近。
往往这个其实反映的是我们现实生活中一个非常基本的一个关系,随着有一些值的增大另外一些值也随着变化。
假如说我们把它变成自变量和因变量,所谓的自变量就是它的变化会引起因变量的变化。也就是说在现实生活中,我们最基本的关系是随着一个变量的变化另外一个变量要么增加,要么减小。当然不变可以算是一种特殊情况,就是变化为0。
那么吃糖的多少、抽烟和工作年限就是整个自变量和因变量的一种关系。现在希望让机器来找到这个关系。
如果把这种关系画出来的话,我们用一个图表画出来就会发现其相关性。
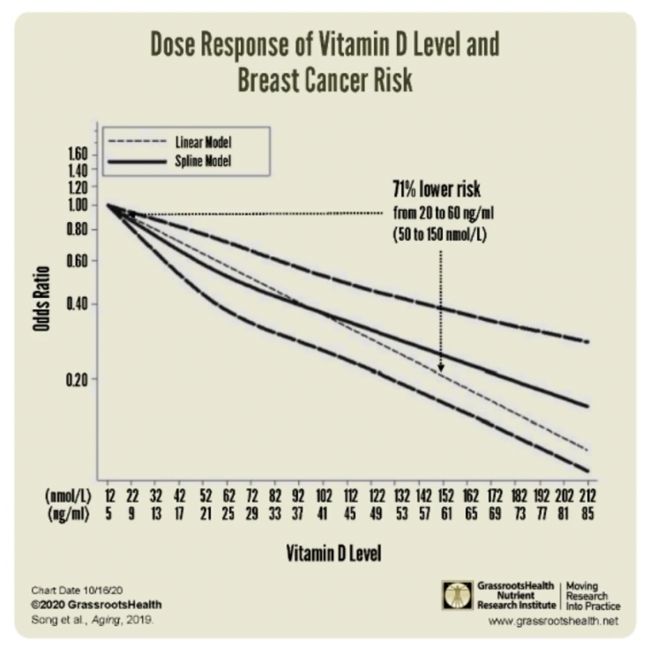
就比如下方这三张图表:
这三个图是非常非常典型的,随着一个量的变化另外的一个量要么减少,要么增加。
这个时候工程师就希望我们能够对现实生活中这种随着一个变量的增加或减少导致另外一个量增加或减小,能够找到一种关系来刻画。
当然之间的这种关系可能会很多,可以是一种线性结构,y = kx+b, 也可以是
其他的什么结构。最简单的一种其实就是线性关系。
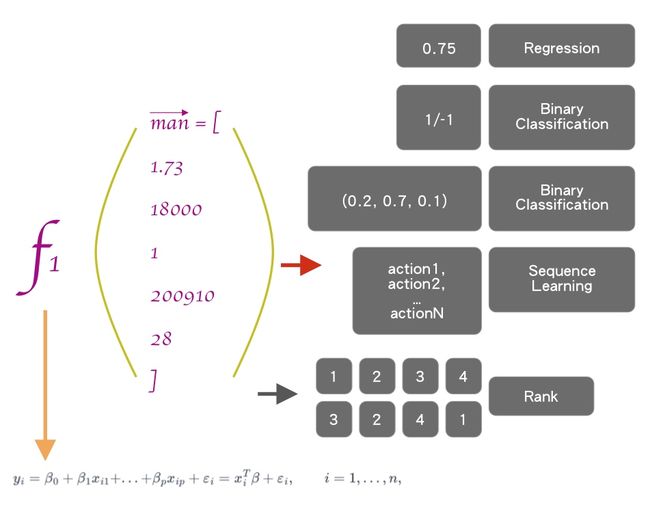
x ⃗ = [ x 0 , x 1 , x 2 , . . . , x n ] f ( x ) = ∑ i ∈ N w i × x i + b \begin{align*} \vec {x} = [x_0, x_1, x_2, ..., x_n] \\ f(x) = \sum_{i \in N} w_i \times x_i +b \end{align*} x=[x0,x1,x2,...,xn]f(x)=i∈N∑wi×xi+b
我们把这种关系称为是线性关系。
为什么称为线性关系呢?假设x现在是一维空间, x ∈ R 1 x \in R^1 x∈R1, 那么f(x)就是一条直线。如果x是二维空间的话, x ∈ R 2 x\in R^2 x∈R2, f(x)就是一个平面。这种关系其实是自然界中最简单的一种关系。
除了这种关系之外,你还可以想象一下,如果我们要刻画x和f(x)之间的关系, 你还能想到哪些函数呢?
比如咱们可以有:
- 二次函数 f ( x ) = a x 2 + b x + c f(x) = ax^2 + bx + c f(x)=ax2+bx+c,
- 三角函数 f ( x ) = s i n ( x ) f(x) = sin(x) f(x)=sin(x),
- 幂函数 f ( x ) = a x f(x) = a^x f(x)=ax,
- 反函数 f ( x ) = t a n h ( x ) f(x) = tanh(x) f(x)=tanh(x),
- 对数函数 f ( x ) = l o g ( x ) f(x) = log(x) f(x)=log(x),
咱们整个来了个数学回顾。这个时候你会发现好像有非常多种函数,甚至我们还可以在这个基础之上做一些复杂的函数, 比如说$f(x) = x{bx3+cx2+dlogx}+e\times log^x_m $。
理论上,我们可以做有无数种可能的关系。
其实就是如何找到因变量和自变量之间的关系,长久以来,这其实是我们整个自然科学界一直在思考探索的一个问题。
像牛顿,笛卡尔、爱因斯坦、波尔这些人其实都是在研究这件事情。当观察到了很多事情,然后期望用一种函数关系能够把它来表证出来。
后来,在14世纪一个非常著名的哲学家就提出来了这样的一个理论,叫做奥卡姆剃刀原理。奥卡姆剃刀原理说的是对于一件事情,你要解释它的关系的话,最简单的:
The explanation requiring the fewest assumptions is most likely to be correct.
这个fewest assumptions指的是什么意思? 就是最少的假设,你可以把它理解成是几个假设, 假如对应到函数上, 就有很多变量。
举个例子,你们单位上有一个同事经常迟到,有三个人对这个同事为什么迟到有不同的说法。
第一个人说这个同事迟到大概率是因为他前一天晚上吃坏了肚子,导致一晚上没睡好,一大早还因为拉肚子迟到了。
第二个人说同事昨天和一个男生出去了,可能玩太晚导致没起来。
第三个说这个同事可能对昨天法的工资有抱怨,去找领导议论没有得到结果,昨天找男朋友安慰了。今天也是因为赌气故意迟到。
那么对于一个女孩子第二天早上迟到,人们就有3种不同的说法。那么大家仔细思考一下,对于你来说,你要相信一个的话,在我们日常生活中你会发现把一件事情想的越复杂往往就错了。
因为比方说第三个条件的,首先昨天发没发工资是一种可能性,然后发了工资她有没有去找老板?找了老板老板有没有怼她?就算怼了她,那她有没有找男朋友?这一系列下来你会发现这个事情如果把它变得因素很多,你对这个事情的估计可能会更错误。
奥卡姆就提出:若无必要,勿增实体。如果对于同一现象有几种不同的假说,我们应该采取最简单的哪一种。那么在我们抽象的函数上,拟合也是这样,我们要拟合一种关系,一种最简单的关系其实往往是最有用的。
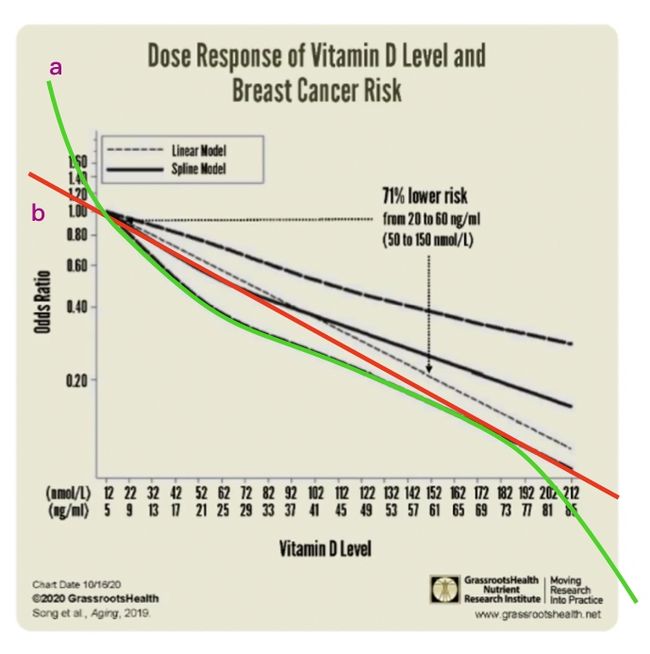
比方说在这种关系上:
在这种关系上,你可以说他是一条直线。
比方说我们看到绿色这条线,比较弯,可以说这条线就是这样的一个函数。但是最简单的一种方法,假设它就是一条直线,就像红色这条线。
我们如果把绿色这条定义为a,把红色这条定义为b。a好像拟合的程度更高一些,b其实是做了一个特别简单的假设,它假设就是一个简单的线性关系。线性关系就是随着一个变量的增多,另外一个也成比例的增多或者减小。
a看起来更复杂,但b在整个状态上看更稳定。a这个函数在没有看到的地方,其实按照趋势就有可能差的特别大。而b虽然在观察到的地方有一些差别,但是因为它这个模型很简单,假设很简单,所以在这些没有观测到的地方你会发现还是和我们整体的趋势会比较接近。
a复杂,在做函数拟合的时候,不管这个关系看起来有多复杂,先假设它是最简单的一种线性关系。当线性关系实在不好的时候,再把它变复杂。
这就是为什么学习机器学习监督式学习要先学习线性拟合的原因。对简单的假设不一定对,但是除非这个简单的假设不行,否则我们就不要给他更复杂的假设。
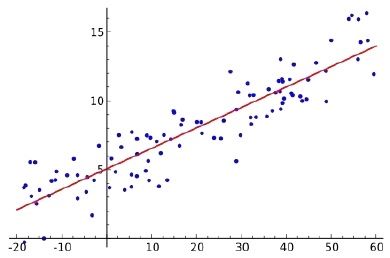
比方说下面这个图:
这四张图中,都可以用一个直线去拟合。当然有的时候,比如说(x2,y2), 当它数据量很多的时候用一个直线效果就会不太好,包括(x4, y4)效果可能也不会太好。
在这个时候,当我们发现它效果很差的时候,再去给他换一个模型。那像(x1,y1),还有(x3, y3),还有如下图这种:
这些其实都可以用一种线性关系来拟合。所谓的线性拟合,就是把函数写成自变量x和它的权重相乘相加,然后再加上一个b。就是我们刚才所描述的: f ( x ) = ∑ i ∈ N w i × x i + b f(x) = \sum_{i\in N} w_i \times x_i + b f(x)=∑i∈Nwi×xi+b;这种形式。这个就是我们的线性模型。
如果Regression输出是一个实数,利用一种线性关系,就是我们图中下方的公式:
y i = β 0 + β 1 x i 1 + . . . + β p x i p + ε i = x i T β + ε i , i = 1 , . . . , n , \begin{align*} y_i = \beta_0+\beta_1x_{i1}+...+\beta_px_{ip}+\varepsilon_i = x_i^T\beta + \varepsilon_i, \qquad i = 1, ..., n, \end{align*} yi=β0+β1xi1+...+βpxip+εi=xiTβ+εi,i=1,...,n,
我们把它的关系假设成是一种线性关系,输出是一系列的实数,这个是一种回归现象,我们就把这个叫做线性回归。
图下方的式子是线性关系,Regression是回归现象。我们就把要拟定的f(x)叫做线性回归。
假如y是一个向量,x是一个矩阵,y等于x矩阵和 β \beta β矩阵做相乘运算。
y = [ y 1 y 2 ⋮ y n ] , y = X β + ε ; X = [ x 1 T x 2 T v d o t s x n T ] = [ 1 x 11 ⋯ x 1 p 1 x 21 ⋯ x 2 p ⋮ ⋮ ⋱ ⋮ 1 x n 1 ⋯ x n p ] , β = [ β 0 β 1 β 2 ⋮ β p ] , ε = [ ε 1 ε 2 ⋮ ε n ] \begin{align*} y & = \begin{bmatrix} y_1 \\ y_2 \\ \vdots y_n\end{bmatrix}, y = X\beta + \varepsilon; \\ \\ X & = \begin{bmatrix} x_1^T \\ x_2^T \\ vdots \\ x_n^T \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \\ \end{bmatrix}, \\ \\ \beta & = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_p \end{bmatrix}, \varepsilon = \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \vdots \\ \varepsilon_n \\ \end{bmatrix} \end{align*} yXβ= y1y2⋮yn ,y=Xβ+ε;= x1Tx2TvdotsxnT = 11⋮1x11x21⋮xn1⋯⋯⋱⋯x1px2p⋮xnp ,= β0β1β2⋮βp ,ε= ε1ε2⋮εn
这个也是咱们之后做深度学习的时候之所以会经常接受矩阵的一个原因。
线性回归,刚给大家把原理讲了。现在咱们来演示一个非常基本的例子。
我给大家演示这个线性回归,用了一个非常经典的数据集。这个数据集叫做波士顿房价问题, 很久前我在学习大数据的时候也成用过这个数据集。
其实我还曾经做过一个一线城市房价的研究,包括北京、上海等地区。但是为什么我没有用这些数据集,而是使用了一个很古老的波士顿地区房价数据集?
因为波士顿这个房价,和room size,地点,地铁,高速路,周围的犯罪率等等有一个比较明显的关系。所以观察关系比较容易。但是北京的房价有个特点,它和远近没有关系,就是五环六环,也有些房子会很贵,三环也有房子会比较便宜。
和房屋的状况关系也不大,就是有的很老但是也是很贵。他唯一一个有关系的就是学区,这是最重要的一个决定因素。基本上周围有学区,这个房子就会非常贵,尤其是在海淀区。
波士顿数据集虽然很老,但是我们主要是为了学习他背后的这个线性回归原理。
北京这个房价要预测其实很简单,就是你用关键字来预测一下,看一下它里边包不包含学区两个字,然后再看一下那个学区排名就可以了。也并不是说说简单用学区就可以,而是学区对于北京房价的影响是最大的,别的因素都没有那么明显。
不过这个数据集在scikit-learn的1.0版本中被弃用,更甚的是在1.2版本中已经删除,所以我们要想使用这个数据集还需要费一番功夫。
我们可以使用公开库openml来进行下载:
import pandas as pd
from sklearn.datasets import fetch_openml
dataset = fetch_openml(name='boston', version=1, as_frame=True, return_X_y=False, parser='pandas')
这其中,name就是数据集的名称, version为版本, return_X_y是下载拆分的特征和标签还是字典,False是默认值,下载的会是字典,如果设定为True,这需要两个变量分别接收特征和标签。
data_x, data_y = fetch_openml(name="boston", version=1, as_frame=True, return_X_y=True, parser="pandas")
然后我们来处理一下数据:
data = dataset['data']
target = dataset['target']
columns = dataset['feature_names']
dataframe = pd.DataFrame(data)
dataframe['price'] = target
dataframe.head()
在我们获取的数据dataframe中,我们可以使用一个corr(), show the correlation of dataframe variables, correlation是相关系数。
那么相关系数的关系就是,如果一个值的增大,会引起另外一个值一定增大,而且是定比例增大,相关系数就越接近于1。如果是0,就是两者之间没有任何关系。那如果是-1呢,就是一个值增大,另外一个值就一定见效,而且减小是成相等比例的。
那我们来看一下dataframe的correlation之间的关系:
dataframe.corr()
当然,我截图不全。小伙伴们下去自己去执行看看。
现在我们得到了一个14乘14的一个矩阵,我们可以通过seaborn的heatmap来图形化,方便我们更直接的看到其相关性。
在这张图中,越接近于黑色就越呈负相关,越接近于这个浅色就越是正相关,越接近于1.
比方说prime和prime是1, 也就说把price当成因变量,再把price也当成自变量的时候这两个值是一个增加另外一个一定增加。
price除了自己本身之外,最亮的是RM,这是和price相关性最大的一个。我们去查询数据源,RM就是小区平均的卧室个数。
换句话说这个小区如果卧室越多,就意味着房子可能越大,就越是有钱人住的。
再接着找一下影响最负相关的是什么?就是哪一个值的增大会引起房价的降低。
最下面的LSTAT是最负面影响的,只要LSTAT增大,房价就会明显的随之下降。LSTAT是什么呢?LSTAT就是一个小区中的低收入人群在周围的额比例, 比例越高,那么房价就会越低。
咱们现在把这两个数值给它全部拿出来:
rm = dataframe['RM']
lstat = dataframe['LSTAT']
现在我们发现,RM是最房价正向影响最多的,LSTAT是对房价负面影响最多的。现在我们要通过这两个值,因为这两个是影响房价最明显的特征,所以我们现在要建立一个模型,要根据我们已知的RM和LSTAT来预测房价是多少。
我们要假设一个关系,要建立一个模型。所谓模型其实就是假设关系。很多模型其实都是现实世界中的一种抽象和简化。
高等数学概率统计,第一册的后半部分专门有一个地方就讲相关系数的。有兴趣的回过头再去看看咱们「AI秘籍」的数学篇。
这里,大家要知道相关系数的意义是什么就行。
我们现在假设和房价之间是一种最简单的线性关系。先从最简单的线性关系开始,假设它是线性关系的话:
def model1(rm, lstat, w1, w2, b):
return w1 * w2 * lstat + b
这样,我们就用代码简单的实现了一个典型的线性关系。
这个时候,我们通过前面所讲的内容:
x ⃗ = [ x 0 , x 1 , x 2 , . . . , x n ] f ( x ) = ∑ i ∈ N w i × x i + b \begin{align*} \vec {x} = [x_0, x_1, x_2, ..., x_n] \\ f(x) = \sum_{i \in N} w_i \times x_i +b \end{align*} x=[x0,x1,x2,...,xn]f(x)=i∈N∑wi×xi+b
我们知道x是一个向量,wi也是一个向量。我们来重新定义一下这个model, 你会发现更简单一些:
def model2(x, w, b):
'''
if x = (rm, lstat)
w = (w1, w2)
'''
return np.dot(x, w.T) + b
我们把模型重新写一下, 如果每一个x就等于(rm, lstat), 然后w就等于(w1,w2),就是x和w是两个向量,那么model1()就可以简写model2()的形式。
就是x1乘以w1加x2乘以w2,再加上b。
那我们写成向量形式,和model1有什么区别,或者说有什么好处呢?它的好处其实就是在后续需要添加数据的时候函数是不需要改动的。
有了这个model,我们的目标是要获得一组w和b,要能够使得对于我们的值的预测最好。
怎么预测呢?
$$
\begin{align*}
loss(\theta) & = \frac{1}{2} \sum(f_{\theta}(xi)-yi)^2 = \frac{1}{2}\sum(\theta ^T - yi)2 \
loss(\theta) & = \frac{1}{2} \sum|f_{\theta}(xi)-yi| = \frac{1}{2}\sum|\theta ^T - y^i|
\end{align*}
$$
做一个loss函数,这个loss函数里, θ \theta θ指的是我们所有的参数。就是在这一组参数下,xi送到f(x)里面,它产生的估计的值,然后再计算和y之间的差别。
也就是为了获得最优的参数集合,比方说是(w, b),我们定义了一个loss函数, 这个loss函数在 θ \theta θ下,我们输入一组x: l o s s ( θ ; x ⃗ ) loss(\theta; \vec{x}) loss(θ;x), 然后它就等于求和,i属于所有的i: ∑ i ∈ N \sum_{i \in N} ∑i∈N, f θ ( x i ) f_{\theta}(x_i) fθ(xi)减去 y i y_i yi之后的平方:
l o s s ( θ ; x ⃗ ) = ∑ i ∈ N ( f θ ( x i ) − y i ) 2 \begin{align*} loss(\theta; \vec {x}) = \sum_{i \in N}(f_{\theta}(x_i) - y_i)^2 \end{align*} loss(θ;x)=i∈N∑(fθ(xi)−yi)2
如果这个 f θ f_{\theta} fθ对x的预测值越好,就说给的x都能非常准确的预测出来值是多少,预测值和实际值完全一样,那么这个时候loss就等于0。因为我们的 f θ ( x i ) f_\theta(x_i) fθ(xi)和 y i y_i yi完全相等。两者相减必定等于0。
当loss特别大的时候,其实是意味着预测值就和真实值差得很远。
在统计学里预估值往往会写成 y ^ \hat y y^,那我们就可以将式子变成如下这种形式:
l o s s ( x ) = 1 n ∑ i ∈ N ( y ^ i − y i ) 2 \begin{align*} loss(x) = \frac{1}{n}\sum_{i \in N}(\hat y_i - y_i)^2 \end{align*} loss(x)=n1i∈N∑(y^i−yi)2
之前的课程里咱们讲过,为了找出变量让loss能够取得最小值,我们可以使用梯度下降的方法。那么我们上面的式子就也可以是如下这种形式:
l o s s ( x ) = 1 n ∑ ( w 1 × x 1 + w 2 × x 2 + b − y i ) 2 \begin{align*} loss(x) = \frac{1}{n}\sum(w_1 \times x_1 + w_2 \times x_2 +b - y_i)^2 \end{align*} loss(x)=n1∑(w1×x1+w2×x2+b−yi)2
现在为了获得一组(w,b), 使得loss最小。那写出loss对w1,w2的偏导, 对b的偏导,就能求解出来了。
那么loss对于W1的偏导等于多少呢?
∂ l o s s ∂ w 1 \begin{align*} \frac{\partial{loss}}{\partial{w_1}} \end{align*} ∂w1∂loss
这个都不用手算,眼睛都能看出来。我们将2放下来,
把后边的指数2放下来, 然后再把X1提出去。如果你还不会算这个,可以去复习一下导数怎么求。可以找一本高数去好好看看,也可以去我之前写的《数学篇》里去好好看一下。
∂ l o s s ∂ w 1 = 2 n ∑ i ∈ N ( w 1 × x i 1 + w 2 × x i 2 + b − y i ) × x i 1 \begin{align*} \frac{\partial{loss}}{\partial{w_1}} = \frac{2}{n}\sum_{i \in N}(w_1 \times x_{i1} + w_2 \times x_{i2} + b - y_i) \times x_{i1} \end{align*} ∂w1∂loss=n2i∈N∑(w1×xi1+w2×xi2+b−yi)×xi1
与此类似,loss对于W2的偏导就等于:
∂ l o s s ∂ w 2 = 2 n ∑ i ∈ N ( w 1 × x i 1 + w 2 × x i 2 + b − y i ) × x i 2 \begin{align*} \frac{\partial{loss}}{\partial{w_2}} = \frac{2}{n}\sum_{i \in N}(w_1 \times x_{i1} + w_2 \times x_{i2} + b - y_i) \times x_{i2} \end{align*} ∂w2∂loss=n2i∈N∑(w1×xi1+w2×xi2+b−yi)×xi2
对于b的偏导, 直接就乘以1了:
∂ l o s s ∂ b = 2 n ∑ i ∈ N ( w 1 × x i 1 + w 2 × x i 2 + b − y i ) \begin{align*} \frac{\partial{loss}}{\partial{b}} = \frac{2}{n}\sum_{i \in N}(w_1 \times x_{i1} + w_2 \times x_{i2} + b - y_i) \end{align*} ∂b∂loss=n2i∈N∑(w1×xi1+w2×xi2+b−yi)
我们之前是要求什么?求rm和lstat对吧?那我们现在就可以将其中的x1和x2替换掉就可以了:
∂ l o s s ∂ w 1 = 2 n ∑ i ∈ N ( w 1 × r m i + w 2 × l s t a t i + b − y i ) × r m i ∂ l o s s ∂ w 2 = 2 n ∑ i ∈ N ( w 1 × r m i + w 2 × l s t a t i + b − y i ) × l s t a t i ∂ l o s s ∂ b = 2 n ∑ i ∈ N ( w 1 × r m i + w 2 × l s t a t i + b − y i ) \begin{align*} \frac{\partial{loss}}{\partial{w_1}} & = \frac{2}{n}\sum_{i \in N}(w_1 \times rm_i + w_2 \times lstat_i + b - y_i) \times rm_i \\ \frac{\partial{loss}}{\partial{w_2}} & = \frac{2}{n}\sum_{i \in N}(w_1 \times rm_i + w_2 \times lstat_i + b - y_i) \times lstat_i \\ \frac{\partial{loss}}{\partial{b}} & = \frac{2}{n}\sum_{i \in N}(w_1 \times rm_i + w_2 \times lstat_i + b - y_i) \end{align*} ∂w1∂loss∂w2∂loss∂b∂loss=n2i∈N∑(w1×rmi+w2×lstati+b−yi)×rmi=n2i∈N∑(w1×rmi+w2×lstati+b−yi)×lstati=n2i∈N∑(w1×rmi+w2×lstati+b−yi)
写成这样之后, 接下来只要在编程的时候实现出来就行了。也就是,把这一段数学翻译成代码。
我们现在来翻译一下loss函数:
def loss(yhat, y):
loss_ = 0
for y_i, yhat_i in zip(y, yhat):
loss_ += (y_i - yhat_i) ** 2
return loss_ / len(yhat)
我们有一个loss, loss的值先等于0,我们循环一下(y, yhat), 然后loss 就加等于 y_i - yhat_i结果的平方。然后loss再除以len(yhat)。
这样就是最简单的一种翻译,之前的loss函数就可以翻译成这样。
不过我们要知道另外一种方法,就是NumPy里提供了一个方法mean(), 意思是求平均值。
假如说里面有12345:mean(1,2,3,4,5),就是把12345这些数字全部加起来,再求它的平均值。
那我们之前的内容就可以写成mean((yhat-y)**2), 其实就是y_i和yhat_i加起来求个平均值。
所以,我们就可以将代码写成如下这样:
def loss(yhat, y):
return np.mean((yhat - y) ** 2)
这个写法就是NumPy的广播方法。咱们在之前的Python篇中有讲到这部分内容,不记得小伙伴可以回头去翻看一下,应该是第26章,大家可以去看一下,为了顺利进行下去,我们这里再提一下。
比如说,我们有两个list:
vec1 = [1, 2, 3]
vec2 = [4, 5, 6]
那么我要进行计算,你会发现会报错:
vec1 - vec2
---
unsupported operand type(s) for -: 'list' and 'list'
当然,我们可以使用for进行循环,但是这样的方法未免太过笨重。而NumPy中就提供了一种广播的方法:
vec1 = np.array([1, 2, 3])
vec2 = np.array([4, 5, 6])
vec1 - vec2
---
array([-3. -3. -3])
将数据改变成NumPy的array,其实就是把它进行向量法,这样去做减法就直接可以减了,这就是咱们代码这样改的一个原因。
接着,咱们要对w求偏导:
def partial_w(x, y, yhat):
return np.array([2 * np.mean((yhat - y) * x[0]), 2 * np.mean((yhat - y) * x[1])])
这里,我们的yhat也就是 y ^ \hat y y^,其实是相当于 w 1 × x i 1 + w 2 × x i 2 + b w_1 \times x_{i1} + w_2 \times x_{i2} + b w1×xi1+w2×xi2+b这一部分,也就是我们预计的值。
预计的值减去实际的值,再乘上xi。假如把rm和lstat一起输入进来的话,x是一个向量,第一个是rm, 第二个是x0。
接下来,对b求导也就很好写了:
def partial_b(x, y, yhat):
return 2 * np.mean((yhat - y))
现在已经定义好了线性模型, 定义好了loss,定义好了偏导。我们现在就初始化一个w,一个一行两列的数组,b默认可以是0,也可以是一个随机值。
w = np.random.random_sample(size = (1, 2))
b = np.random.random()
不过一般来说,w初始化成一个normal, 但是b一般要初始化成0。至于为什么,咱们大概讲到深度学习的时候详细的来讲。
然后现在来得到yhat,这个时候我们就要得到一个x,w是有的,b是有的。
yhat = model(x, w, b)
x怎么求解呢? 就需要带一个知识点了,这个知识点就叫做batch training。就是在做机器学习的时候每次取一个或者少数几个数字来进行学习。
这个是为什么呢?其实理论上是可以把所有的数据一起放进去的,但是在真正的工作中,比方说阿里云里面那个数据那么多,在做模型的时候一下放进去,既存不下,速度还会很慢。所以随机的找几个。那这样,你就可以得到不同的yhat了:
for i in range(50):
for batch in range(len(rm)):
# batch training
index = random.choice(range(len(rm)))
rm_x = rm[index]
lstat_x = lstat[index]
x = np.array([rm_x, lstat_x])
yhat = model(x, w, b)
print(yhat)
可以得到不同的yhats, 因为每次随机取的值不一样。因为他的x不一样,所以估计出来的y也不一样。
可以加一个loss(yhat, y), 我们来看一下它的loss。
y = target[index]
loss_ = loss(yhat, y)
print(loss_)
---
976.1638310150673
...
1.7070546224396366
...
121.30523219624953
loss一直比较大,偶尔会出现一个比较小的值,也是昙花一现,因为w是随机的, 就是loss一直在随机波动。
现在咱们要做一件事:
learning_rate = 1e-5
w = w + -1 * partial_w(x, y, yhat) * learning_rate
b = b + -1 * partial_b(x, y, yhat) * learning_rate
然后我们每100下来打印一下:
if batch % 100 == 0:
print('Epoch: {} Batch: {}, loss: {}'.format(i, batch, loss_))
讲到这, 线性回归基本上原理就已经讲完了,咱们下节课再见。下节课,咱们先来总结一下本节课内容,然后咱们开讲「逻辑回归」。