ZHHHHHJ66

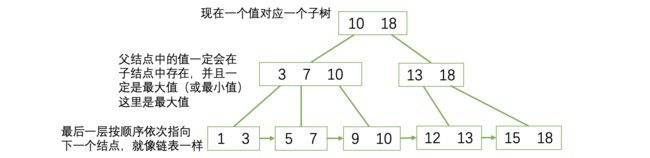
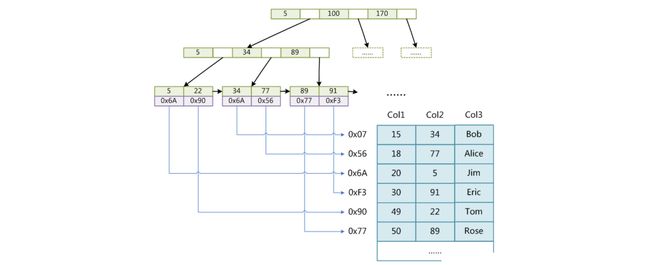
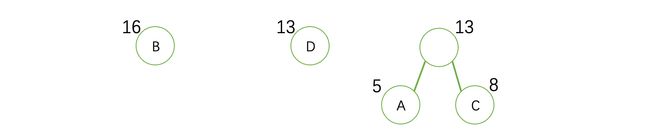
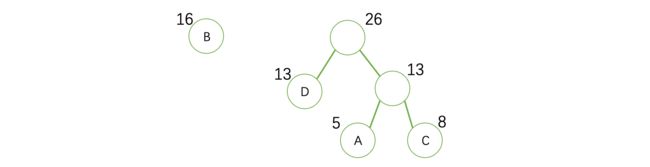
数据结构与算法基础知识

线性结构篇

什么是数据结构与算法

回顾我们之前的C语言程序设计阶段，我们已经接触过基本数据类型，并且能够使用结构体对数据进行组织，我们可以很轻松地使用一个结构体来存放一个学生的完整数据，在数据结构学习阶段，我们还会进一步地研究。

数据结构

那么，我们来看看，什么是数据结构呢？

数据结构(data structure)是带有结构特性的数据元素的集合，它研究的是数据的逻辑结构和数据的物理结构以及它们之间的相互关系。

比如现在我们需要保存100个学生的数据，那么你首先想到的肯定是使用数组吧！没错，没有什么比数组更适合存放这100个学生的数据了，但是如果我们现在有了新的需求呢？我们不仅仅是存放这些数据，我们还希望能够将这些数据按顺序存放，支持在某个位置插入一条数据、删除一条数据、修改一条数据等，这时候，数组就显得有些乏力了。

我们需要一种更好的数据表示和组织方式，才能做到类似于增删改查这样的操作，而完成这些操作所用到的方法，我们称其为“算法”，所以数据结构和算法，一般是放在一起进行讲解的。

算法

比如现在我们希望你求出1-100所有数字的和，请通过程序来实现：

int main() {
  int sum = 0;
  for (int i = 1; i <= 100; ++i) sum += i;
  printf("%d", sum);
}

我们很容易就能编写出这样的程序，实际上只需要一个for循环就能搞定了，而这就是我们设计的算法。

在之前的C语言程序设计阶段，我们其实已经学习了许多算法，包括排序算法、动态规划等。

当然，解决问题的算法并不是只有一种，实际上我们上面的方式并不是最优的算法，如果想要求得某一段整数的和，其实使用高斯求和公式能够瞬间得到结果：
$\sum=\frac{(首项+末项)\times项数}{2}$
所以，我们完全没必要循环那么多次进行累加计算，而是直接使用数学公式：

int main() {
  printf("%d", (1 + 100) * 100 / 2);
}

所以，算法的尽头还得是数学啊。

可见，不同的算法，执行的效率也是有很大差别的，这里我们就要提到算法的复杂度了。衡量一个算法的复杂程度需要用到以下两个指标：

时间复杂度T(n)：算法程序在执行时消耗的时间长度，一般与输入数据的规模n有关。
空间复杂度S(n)：算法程序在执行时占用的存储单元长度，同样与数据的输入规模n有关，大部分情况下，我们都是采取空间换时间的算法。

比如我们上面的两种算法，第一种需要执行n次循环，每轮循环进行一次累加操作，而第二种只需要进行一次计算即可。实际中我们计算时间复杂度时，其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么这里我们使用O渐进表示法。

大O符号（Big O notation）：是用于描述函数渐进行为的数学符号。

而这里的循环次数，实际上就是我们需要知道的大致执行次数，所以第一种算法的时间复杂度为：O(n)，其中n就是项数，因为它需要执行n次计算才能得到最后的结果。而第二种算法的时间复杂度为：O(1)，因为它只需要执行一次计算（更准确的说它的执行次数是一个常数，跟项数n毫无关系），显然，当n变得非常大时，第二种方法的计算速度远超第一种。

再比如我们之前使用的冒泡排序算法，需要进行两轮循环，而循环的次数在经过优化之后为(n - 1)(n - 1)/2，得到的结果中包含了一个n的平方，此时这种算法的时间复杂度就来到O(n^2)了。

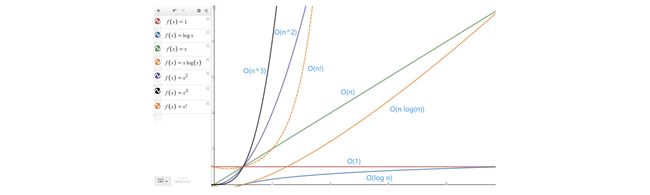
在不同的空间复杂度下，可能n小的时候还没什么感觉，但是当n变得非常大时，差距就不是一点半点了，我们来看看常用函数的增长曲线：

所以我们在设计算法的时候，一定要考虑到时间和空间复杂度的问题，这里列出常用函数的增长表：

函数	类型	解释
$\Omicron(1)$	常数阶	如果算法能够优化到这个程度，那么基本上算是最快的算法了。
$\Omicron(\log_{2}n)$	对数阶	仅次于常数阶的速度，我们后面会介绍的二分搜索算法，就能够到达这个级别。
$\Omicron(n)$	线性阶	我们后面介绍的线性表插入、删除数据，包括动态规划类算法能够达到线性阶。
$\Omicron(n\log_{2}n)$	线性对数阶	相当于在对数阶算法外层套了一层线性阶循环。
$\Omicron(n^2)$	平方阶	我们前面学习的冒泡排序，需要进行两重循环，实际上就是平方阶。
$\Omicron(n^3)$	立方阶	从立方阶开始，时间复杂度就开始变得有点大了。
$\Omicron(2^n)$	指数阶	我们前面介绍的斐波那契数列递归算法，就是一个指数阶的算法，因为它包含大量的重复计算。
$\Omicron(n!)$	阶乘	这个增长速度比指数阶还恐怖，但是一般很少有算法能达到这个等级。

我们在编写算法时，一定要注意算法的时间复杂度，当时间复杂度太大时，可能计算机就很难在短时间内计算出结果了。

案例：二分搜索算法

现在有一个从小到大排序的数组，给你一个目标值target，现在请你找到这个值在数组中的对应下标，如果没有，请返回-1：

int search(int* nums, int numsSize, int target){
  //请实现查找算法
}

int main() {
  int arr[] = {1, 3, 4, 6, 7,8, 10, 11, 13, 15}, target = 3;
  printf("%d", search(arr, 10, target));
}

此时，最简单的方法就是将数组中的元素一个一个进行遍历，总有一个是，如果遍历完后一个都没有，那么就结束：

int search(int* nums, int numsSize, int target){
  for (int i = 0; i < len; ++i) {
      if(nums[i] == target) return i;   //循环n次，直到找到为止
  }
  return -1;
}

虽然这样的算法简单粗暴，但是并不是最好的，我们需要遍历n次才能得到结果，时间复杂度为 $\Omicron(n)$ ，我们可以尝试将其优化到更低的时间复杂度。这里我们利用它有序的特性，实际上当我们查找到大于目标target的数时，就没必要继续寻找了：

int search(int* nums, int numsSize, int target){
  for (int i = 0; i < len; ++i) {
      if(nums[i] == target) return i;
      if(nums[i] > target) break;
  }
  return -1;
}

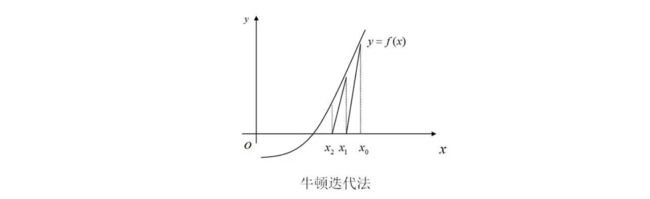
这样循环进行的次数也许就会减小了，但是如果我们要寻找的目标target刚好是最后几个元素呢？这时时间复杂度又来到到了 $\Omicron(n)$ ，那么有没有更好的办法呢？我们依然可以继续利用数组有序的特性，既然是有序的，那么我们不妨随机在数组中找一个数，如果这个数大于目标，那么就不再考虑右边的部分，如果小于目标，那么就考虑左边的部分，然后继续在另一部分中再次随机找一个数，这样每次都能将范围缩小，直到找到为止（其思想就比较类似于牛顿迭代法，再次强调数学的重要性）

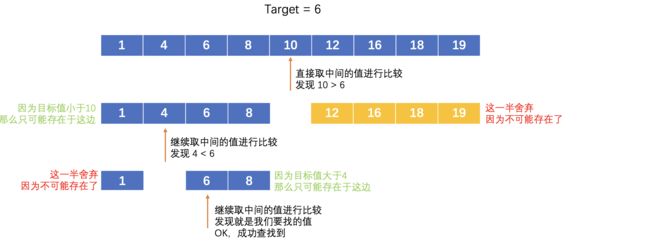
而二分思想就是将一个有序数组不断进行平分，直到找到为止，这样我们每次寻找的范围会不断除以2，所以查找的时间复杂度就降到了 $\Omicron(\log_{2}n)$ ，相比一个一个比较，效率就高了不少：

好了，那么现在我们就可以利用这种思想，编写出二分搜索算法了，因为每一轮都在进行同样的搜索操作，只是范围不一样，所以这里直接采用递归分治算法：

int binarySearch(int * nums, int target, int left, int right){  //left代表左边界，right代表右边界
  if(left > right) return -1;   //如果左边大于右边，那么肯定就找完了，所以直接返回
  int mid = (left + right) / 2;   //这里计算出中间位置
  if(nums[mid] == target) return mid;   //直接比较，如果相等就返回下标
  if(nums[mid] > target)    //这里就是大于或小于的情况了，这里mid+1和mid-1很多人不理解，实际上就是在下一次寻找中不算上当前的mid，因为这里已经比较过了，所以说左边就-1，右边就+1
      return binarySearch(nums, target, left, mid - 1);   //如果大于，那么说明肯定不在右边，直接去左边找
  else
      return binarySearch(nums, target, mid + 1, right);  //如果小于，那么说明肯定不在左边，直接去右边找
}

int search(int* nums, int numsSize, int target){
  return binarySearch(nums, target, 0, numsSize - 1);
}

当然也可以使用while循环来实现二分搜索，如果需要验证自己的代码是否有问题，可以直接在力扣上提交代码：https://leetcode.cn/problems/binary-search/

线性表

那么作为数据结构的开篇，我们就从最简单的线性表开始介绍。

还记得我们开篇提了一个问题吗？

我们还希望能够将这些数据按顺序存放，支持在某个位置插入一条数据、删除一条数据、修改一条数据等，这时候，数组就显得有些乏力了。

数组无法做到这么高级的功能，那么我们就需要定义一种更加高级的数据结构来做到，我们可以使用线性表（Linear List）

线性表是由同一类型的数据元素构成的有序序列的线性结构。线性表中元素的个数就是线性表的长度，表的起始位置称为表头，表的结束位置称为表尾，当一个线性表中没有元素时，称为空表。

线性表一般需要包含以下功能：

**初始化线性表：**将一个线性表进行初始化，得到一个全新的线性表。
**获取指定位置上的元素：**直接获取线性表指定位置i上的元素。
**获取元素的位置：**获取某个元素在线性表上的位置i。
**插入元素：**在指定位置i上插入一个元素。
**删除元素：**删除指定位置i上的一个元素。
**获取长度：**返回线性表的长度。

也就是说，现在我们需要设计的是一种功能完善的表结构，它不像是数组那么低级，而是真正意义上的表：

简单来说它就是列表，比如我们的菜单，我们在点菜时就需要往菜单列表中添加菜品或是删除菜品，这时列表就很有用了，因为数组长度固定、操作简单，而我们添加菜品、删除菜品这些操作又要求长度动态变化、操作多样。

那么，如此高级的数据结构，我们该如何去实现呢？实现线性表的结构一般有两种，一种是顺序存储实现，还有一种是链式存储实现，我们先来看第一种，也是最简单的的一种。

顺序表

前面我们说到，既然数组无法实现这样的高级表结构，那么我就基于数组，对其进行强化，也就是说，我们存放数据还是使用数组，但是我们可以为其编写一些额外的操作来强化为线性表，像这样底层依然采用顺序存储实现的线性表，我们称为顺序表。

这里我们可以先定义一个新的结构体类型，将一些需要用到的数据保存在一起，这里我们以int类型的线性表为例：

typedef int E;  //这里我们的元素类型就用int为例吧，先起个别名

struct List {
  E array[10];   //实现顺序表的底层数组
  int capacity;   //表示底层数组的容量
};

为了一会使用方便，我们可以给其起一个别名：

typedef struct List * ArrayList; //因为是数组实现，所以就叫ArrayList，这里直接将List的指针起别名

然后我们就可以开始编写第一个初始化操作了：

void initList(ArrayList list){
  list->capacity = 10;   //直接将数组的容量设定为10即可
}

但是我们发现一个问题，这样的话我们的顺序表长度不就是固定为10的了吗？而前面我们线性表要求的是长度是动态增长的，那么这个时候怎么办呢？我们可以直接使用一个指针来指向底层数组的内存区域，当装不下的时候，我们可以创建一个新的更大的内存空间来存放数据，这样就可以实现扩容了，所以我们来修改一下：

struct List {
  E * array;   //指向顺序表的底层数组
  int capacity;   //数组的容量
};

接着我们修改一下初始化函数：

void initList(ArrayList list){  //这里就默认所有的顺序表初始大小都为10吧，随意
  list->array = malloc(sizeof(E) * 10);   //使用malloc函数申请10个int大小的内存空间，作为底层数组使用
  list->capacity = 10;    //容量同样设定为10
}

但是还没完，因为我们的表里面，默认情况下是没有任何元素的，我们还需要一个变量来表示当前表中的元素数量：

struct List {
  E * array;   //指向顺序表的底层数组
  int capacity;   //数组的容量
  int size;   //表中的元素数量
};

typedef struct List * ArrayList;

void initList(ArrayList list){  //这里就默认所有的顺序表初始大小都为10吧，随意
  list->array = malloc(sizeof(int) * 10);   //使用malloc函数申请10个int大小的内存空间，作为底层数组使用
  list->capacity = 10;    //容量同样设定为10
  list->size = 0;   //元素数量默认为0
}

还有一种情况我们需要考虑，也就是说如果申请内存空间失败，那么需要返回一个结果告诉调用者：

_Bool initList(ArrayList list){
  list->array = malloc(sizeof(int) * 10);
  if(list->array == NULL) return 0;  //需要判断如果申请的结果为NULL的话表示内存空间申请失败
  list->capacity = 10;
  list->size = 0;
  return 1;   //正常情况下返回true也就是1
}

这样，一个比较简单的顺序表就定义好，我们可以通过initList函数对其进行初始化：

int main() {
  struct List list;   //创建新的结构体变量
  if(initList(&list)){   //对其进行初始化，如果失败就直接结束
    	...
  } else{
      printf("顺序表初始化失败，无法启动程序！");
  }
}

接着我们来编写一下插入和删除操作，对新手来说也是比较难以理解的操作：

我们先设计好对应的函数：

void insertList(ArrayList list, E element, int index){
  	//list就是待操作的表，element就是需要插入的元素，index就是插入的位置（注意顺序表的index是按位序计算的，从1开始，一般都是第index个元素）
}

我们按照上面的思路来编写一下代码：

void insertList(ArrayList list, E element, int index){
  for (int i = list->size; i > index - 1; i--)  //先使用for循环将待插入位置后续的元素全部丢到后一位
      list->array[i] = list->array[i - 1];
  list->array[index - 1] = element;    //挪完之后，位置就腾出来了，直接设定即可
  list->size++;   //别忘了插入之后相当于多了一个元素，记得size + 1
}

现在我们可以来测试一下了：

void printList(ArrayList list){   //编写一个函数用于打印表当前的数据
  for (int i = 0; i < list->size; ++i)   //表里面每个元素都拿出来打印一次
      printf("%d ", list->array[i]);
  printf("\n");
}

int main() {
  struct List list;
  if(initList(&list)){
      insertList(&list, 666, 1);  //每次插入操作后都打印一下表，看看当前的情况 
      printList(&list);
      insertList(&list, 777, 1);
      printList(&list);
      insertList(&list, 888, 2);
      printList(&list);
  } else{
      printf("顺序表初始化失败，无法启动程序！");
  }
}

运行结果如下：

虽然这样看起来没什么问题了，但是如果我们在非法的位置插入元素会出现问题：

insertList(&list, 666, -1);   //第一个位置就是0，怎么可能插入到-1这个位置呢，这样肯定是不正确的，所以我们需要进行判断
printList(&list);

我们需要检查一下插入的位置是否合法：

转换成位序，也就是[1, size + 1]这个闭区间，所以我们在一开始的时候进行判断：

_Bool insertList(ArrayList list, E element, int index){
  if(index < 1 || index > list->size + 1) return 0;   //如果在非法位置插入，返回0表示插入操作执行失败
  for (int i = list->size; i > index - 1; i--)
      list->array[i] = list->array[i - 1];
  list->array[index - 1] = element;
  list->size++;
  return 1;   //正常情况返回1
}

我们可以再来测试一下：

if(insertList(&list, 666, -1)){
  printList(&list);
} else{
  printf("插入失败！");
}

不过我们还是没有考虑到一个情况，那么就是如果我们的表已经装满了，也就是说size已经达到申请的内存空间最大的大小了，那么此时我们就需要考虑进行扩容了，否则就没办法插入新的元素了：

_Bool insertList(ArrayList list, E element, int index){
  if(index < 1 || index > list->size + 1) return 0;
  if(list->size == list->capacity) {   //如果size已经到达最大的容量了，肯定是插不进了，那么此时就需要扩容了
      int newCapacity = list->capacity + (list->capacity >> 1);   //我们先计算一下新的容量大小，这里我取1.5倍原长度，当然你们也可以想扩多少扩多少
      E * newArray = realloc(list->array, sizeof(E) * newCapacity);  //这里我们使用新的函数realloc重新申请更大的内存空间
      if(newArray == NULL) return 0;   //如果申请失败，那么就确实没办法插入了，只能返回0表示插入失败了
      list->array = newArray;
      list->capacity = newCapacity;
  }
  for (int i = list->size; i > index - 1; i--)
      list->array[i] = list->array[i - 1];
  list->array[index - 1] = element;
  list->size++;
  return 1;
}

realloc函数可以做到控制动态内存开辟的大小，重新申请的内存空间大小就是我们指定的新的大小，并且原有的数据也会放到新申请的空间中，所以非常方便。当然如果因为内存不足之类的原因导致内存空间申请失败，那么会返回NULL，所以别忘了进行判断。

这样，我们的插入操作就编写完善了，我们可以来测试一下：

int main() {
  struct List list;
  if(initList(&list)){
      for (int i = 0; i < 30; ++i)
          insertList(&list, i, i);
      printList(&list);
  } else{
      printf("顺序表初始化失败，无法启动程序！");
  }
}

成功得到结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-s2M1cNaW-1683974332471)(null)]

这样，我们就完成了顺序表的插入操作，接着我们来编写一下删除操作，其实删除操作也比较类似，也需要对元素进行批量移动，但是我们不需要考虑扩容问题，我们先设计好函数：

void deleteList(ArrayList list, int index){
  	//list就是待操作的表，index是要删除的元素位序
}

按照我们上面插入的思路，我们反过来想一想然后实现删除呢？首先是删除的范围：

换算成位序就是[1, size]这个闭区间内容，所以我们先来限定一下合法范围：

_Bool deleteList(ArrayList list, int index){
  if(index < 1 || index > list->size) return 0;

  return 1;  //正常情况返回1
}

接着就是删除元素之后，我们还需要做什么呢？我们应该将删除的这个元素后面的全部元素前移一位：

我们按照这个思路，来编写一下删除操作：

_Bool deleteList(ArrayList list, int index){
  if(index < 1 || index > list->size) return 0;
  for (int i = index - 1; i < list->size - 1; ++i)
      list->array[i] = list->array[i + 1];   //实际上只需要依次把后面的元素覆盖到前一个即可
  list->size--;   //最后别忘了size - 1
  return 1;
}

删除相比插入要简单一些，我们来测试一下吧：

for (int i = 0; i < 10; ++i)  //先插10个
  insertList(&list, i, i);
deleteList(&list, 5);   //这里删除5号元素
printList(&list);

成功得到结果：

OK，那么插入和删除操作我们就成功完成了，还有一些比较简单的功能，我们这里也来依次实现一下，首先是获取长度：

int sizeList(ArrayList list){
  return list->size;   //直接返回size就完事
}

接着是按位置获取元素和查找指定元素的位置：

E * getList(ArrayList list, int index){
  if(index < 1 || index > list->size) return NULL;   //如果超出范围就返回NULL
  return &list->array[index - 1];
}

int findList(ArrayList list, E element){
  for (int i = 0; i < list->size; ++i) {   //一直遍历，如果找到那就返回位序
      if(list->array[i] == element) return i + 1;
  }
  return -1;  //如果遍历完了都没找到，那么就返回-1
}

这样，我们的线性表就实现完成了，完整代码如下：

#include 
#include 

typedef int E;

struct List {
  E * array;
  int capacity;
  int size;
};

typedef struct List * ArrayList;

_Bool initList(ArrayList list){
  list->array = malloc(sizeof(E) * 10);
  if(list->array == NULL) return 0;
  list->capacity = 10;
  list->size = 0;
  return 1;
}

_Bool insertList(ArrayList list, E element, int index){
  if(index < 1 || index > list->size + 1) return 0;

  if(list->size == list->capacity) {
      int newCapacity = list->capacity + (list->capacity >> 1);
      E * newArray = realloc(list->array, newCapacity * sizeof(E));
      if(newArray == NULL) return 0;
      list->array = newArray;
      list->capacity = newCapacity;
  }

  for (int i = list->size; i > index - 1; --i)
      list->array[i] = list->array[i - 1];
  list->array[index - 1] = element;
  list->size++;
  return 1;
}

_Bool deleteList(ArrayList list, int index){
  if(index < 1 || index > list->size) return 0;
  for (int i = index - 1; i < list->size - 1; ++i)
      list->array[i] = list->array[i + 1];
  list->size--;
  return 1;
}

int sizeList(ArrayList list){
  return list->size;
}

E * getList(ArrayList list, int index){
  if(index < 1 || index > list->size) return NULL;
  return &list->array[index - 1];
}

int findList(ArrayList list, E element){
  for (int i = 0; i < list->size; ++i) {
      if(list->array[i] == element) return i + 1;
  }
  return -1;
}

**问题：**请问顺序实现的线性表，插入、删除、获取元素操作的时间复杂度为？

**插入：**因为要将后续所有元素都向后移动，所以平均时间复杂度为 $O (n)$
**删除：**同上，因为要将所有元素向前移动，所以平均时间复杂度为 $O (n)$
**获取元素：**因为可以利用数组特性直接通过下标访问到对应元素，所以时间复杂度为 $O (1)$

顺序表习题：

在一个长度为n的顺序表中，向第i个元素前插入一个新的元素时，需要向后移动多少个元素？

A. n - i B. n - i + 1 C. n - i - 1 D. i

注意这里要求的是向第i个元素前插入（第i个表示的是位序，不是下标，不要搞混了，第1个元素下标就为0），这里我们假设n为3，i为2，那么也就是说要在下标为1的这个位置上插入元素，那么就需要移动后面的2个元素，所以答案是B

顺序表是一种（）的存储结构？

A. 随机存取 B. 顺序存取 C. 索引存取 D. 散列存取

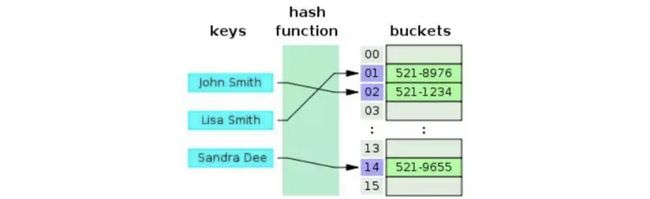
首先顺序表底层是基于数组实现的，那么它肯定是支持随机访问的，因为我们可以直接使用下标想访问哪一个就访问哪一个，所以选择A，不要看到名字叫做顺序表就选择顺序存取，因为它并不需要按照顺序来进行存取，链表才是。这里也没有建立索引去访问元素，也更不可能是散列存取了，散列存取我们会在后面的哈希表中进行介绍

链表

前面我们介绍了如何使用数组实现线性表，我们接着来看第二种方式，我们可以使用链表来实现，那么什么是链表呢？

链表不同于顺序表，顺序表底层采用数组作为存储容器，需要分配一块连续且完整的内存空间进行使用，而链表则不需要，它通过一个指针来连接各个分散的结点，形成了一个链状的结构，每个结点存放一个元素，以及一个指向下一个结点的指针，通过这样一个一个相连，最后形成了链表。它不需要申请连续的空间，只需要按照顺序连接即可，虽然物理上可能不相邻，但是在逻辑上依然是每个元素相邻存放的，这样的结构叫做链表（单链表）。

链表分为带头结点的链表和不带头结点的链表，戴头结点的链表就是会有一个头结点指向后续的整个链表，但是头结点不存放数据：

而不带头结点的链表就像上面那样，第一个节点就是存放数据的结点，一般设计链表都会采用带头结点的结构，因为操作更加方便。

那么我们就来尝试编写一个带头结点的链表：

typedef int E;   //这个还是老样子

struct ListNode {
  E element;   //保存当前元素
  struct ListNode * next;   //指向下一个结点的指针
};

typedef struct Node * Node;   //这里我们直接为结点指针起别名，可以直接作为表实现

同样的，我们先将初始化函数写好：

void initList(Node head){
  head->next = NULL;   //头结点默认下一个为NULL
}

int main() {
  struct ListNode head;   //这里创建一个新的头结点，头结点不存放任何元素，只做连接，连接整个链表
  initList(&head);  //先进行初始化
}

接着我们来设计一下链表的插入和删除，我们前面实现了顺序表的插入，那么链表的插入该怎么做呢？

我们可以先修改新插入的结点的后继结点（也就是下一个结点）指向，指向原本在这个位置的结点：

接着我们可以将前驱结点（也就是上一个结点）的后继结点指向修改为我们新插入的结点：

这样，我们就成功插入了一个新的结点，现在新插入的结点到达了原本的第二个位置上：

按照这个思路，我们来实现一下，首先设计一下函数：

void insertList(Node head, E element, int index){
//head是头结点，element为待插入元素，index是待插入下标
}

接着我们需要先找到待插入位置的前驱结点：

_Bool insertList(Node head, E element, int index){
  if(index < 1) return 0;   //如果插入的位置小于1，那肯定是非法的
  while (--index) {   //通过--index的方式不断向后寻找前驱结点
      head = head->next;   //正常情况下继续向后找
    	if(head == NULL) return 0;  
    	//如果在寻找的过程中发型已经没有后续结点了，那么说明index超出可插入的范围了，也是非法的，直接润
  }
  
  return 1;
}

在循环操作完成后，如果没问题那么会找到对应插入位置的前驱结点，我们只需要按照上面分析的操作来编写代码即可：

_Bool insertList(Node head, E element, int index){
  if(index < 1) return 0;
  while (--index) {
      head = head->next;
    	if(head == NULL) return 0;
  }
  Node node = malloc(sizeof (struct ListNode));
  if(node == NULL) return 0;   //创建一个新的结点，如果内存空间申请失败返回0
  node->element = element;   //将元素保存到新创建的结点中
  node->next = head->next;   //先让新插入的节点指向原本位置上的这个结点
  head->next = node;   //接着将前驱结点指向新的这个结点
  return 1;
}

这样，我们就编写好了链表的插入操作了，我们可以来测试一下：

void printList(Node head){
  while (head->next) {
      head = head->next;
      printf("%d ", head->element);   //因为头结点不存放数据，所以从第二个开始打印
  }
}

int main() {
  struct ListNode head;
  initList(&head);
  for (int i = 0; i < 3; ++i) {
      insertList(&head, i * 100, i);   //依次插入3个元素
  }
  printList(&head);   //打印一下看看
}

成功得到结果：

那么链表的插入我们研究完了，接着就是结点的删除了，那么我们如何实现删除操作呢？实际上也会更简单一些，我们可以直接将待删除节点的前驱结点指向修改为待删除节点的下一个：

这样，在逻辑上来说，待删除结点其实已经不在链表中了，所以我们只需要释放掉待删除结点占用的内存空间就行了：

那么我们就按照这个思路来编写一下程序，首先还是设计函数：

void deleteList(Node head, int index){
  //head就是头结点，index依然是待删除的结点位序
}

首先我们还是需要找到待删除结点的前驱结点：

_Bool deleteList(Node head, int index){
  if(index < 1) return 0;   //大体和上面是一样的
  while (--index) {
      head = head->next;
      if(head == NULL) return 0;
  }
  if(head->next == NULL) return 0;  //注意删除的范围，如果前驱结点的下一个已经是NULL了，那么也说明超过了范围

  return 1;
}

最后就是按照我们上面说的删除结点了：

_Bool deleteList(Node head, int index){
  if(index < 0) return 0;
  while (index--) {
      head = head->next;
      if(head == NULL) return 0;
  }
  if(head->next == NULL) return 0;
  Node tmp = head->next;   //先拿到待删除结点
  head->next = head->next->next;   //直接让前驱结点指向下一个的下一个结点
  free(tmp);   //最后使用free函数释放掉待删除结点的内存
  return 1;
}

这样，我们就成功完成了链表的删除操作：

int main() {
  struct ListNode head;
  initList(&head);
  for (int i = 0; i < 3; ++i) {
      insertList(&head, i * 100, i);
  }
  deleteList(&head, 0);   //这里我们尝试删除一下第一个元素
  printList(&head);
}

最后得到结果也是正确的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cWaNQYzN-1683974308403)(null)]

接着就是链表的一些其他操作了，这里我们也来实现一下，首先是获取对应位置上的元素：

E * getList(Node head, int index){
  if(index < 1) return NULL;   //如果小于0那肯定不合法，返回NULL
  do {
      head = head->next;  //因为不算头结点，所以使用do-while语句
      if(head == NULL) return NULL;  //如果已经超出长度那肯定也不行
  } while (--index);  //到达index就结束
  return &head->element;
}

接着是查找对应元素的位置：

int findList(Node head, E element){
  head = head->next;    //先走到第一个结点
  int i = 1;   //计数器
  while (head) {
      if(head->element == element) return i;   //如果找到，那么就返回i
      head = head->next;   //没找到就继续向后看
      i++;   //i记住要自增
  }
  return -1;   //都已经走到链表尾部了，那么就确实没找到了，返回-1
}

接着是求链表的长度，这个太简单了：

int sizeList(Node head){
  int i = 0;  //从0开始
  while (head->next) {   //如果下一个为NULL那就停止
      head = head->next;
      i++;   //每向后找一个就+1
  }
  return i;
}

这样，我们的链表就编写完成了，整个代码如下：

#include 
#include 

typedef int E;

struct ListNode {
  E element;
  struct ListNode * next;
};

typedef struct ListNode * Node;

void initList(Node node){
  node->next = NULL;
}

_Bool insertList(Node head, E element, int index){
  if(index < 1) return 0;
  while (--index) {
      head = head->next;
      if(head == NULL) return 0;
  }

  Node node = malloc(sizeof(struct ListNode));
  if(node == NULL) return 0;
  node->element = element;
  node->next = head->next;
  head->next = node;
  return 1;
}

_Bool deleteList(Node head, int index){
  if(index < 1) return 0;   //大体和上面是一样的
  while (--index) {
      head = head->next;
      if(head == NULL) return 0;
  }
  if(head->next == NULL) return 0;

  Node tmp = head->next;
  head->next = head->next->next;
  free(tmp);
  return 1;
}

E * getList(Node head, int index){
  if(index < 1) return 0;
  do {
      head = head->next;
      if(head == NULL) return 0;
  } while (--index);
  return &head->element;
}

int findList(Node head, E element){
  head = head->next;
  int i = 1;
  while (head) {
      if(head->element == element) return i;
      head = head->next;
      i++;
  }
  return -1;
}

int sizeList(Node head){
  int i = -1;
  while (head) {
      head = head->next;
      i++;
  }
  return i;
}

**问题：**请问链式实现的线性表，插入、删除、获取元素操作的时间复杂度为？

**插入：**因为要寻找对应位置的前驱结点，所以平均时间复杂度为 $O (n)$ ，但是不需要做任何的移动操作，效率肯定是比顺序表要高的。
**删除：**同上，所以平均时间复杂度为 $O (n)$
**获取元素：**由于必须要挨个向后寻找，才能找到对应的结点，所以时间复杂度为 $O (n)$ ，不支持随机访问，只能顺序访问，比顺序表慢。

问题：什么情况下使用顺序表，什么情况下使用链表呢？

通过分析顺序表和链表的特性我们不难发现，链表在随机访问元素时，需要通过遍历来完成，而顺序表则利用数组的特性直接访问得到，所以，当我们读取数据多于插入或是删除数据的情况下时，使用顺序表会更好。
而顺序表在插入元素时就显得有些鸡肋了，因为需要移动后续元素，整个移动操作会浪费时间，而链表则不需要，只需要修改结点指向即可完成插入，所以在频繁出现插入或删除的情况下，使用链表会更好。

链表练习题：

在一个长度为n (n>1)的单链表上，设有头和尾两个指针，执行（）操作与链表的长度有关？

A．删除单链表中的第一个元素
B．删除单链表中的最后一个元素
C．在单链表第一个元素前插入一个新元素
D．在单链表最后一个元素后插入一个新元素

注意题干，现在有指向链表头尾的两个指针，那么A、C肯定是可以直接通过头结点找到的，无论链表长度如何都不影响，D也可以直接通过尾指针进行拼接，只有B需要尾指针的前驱结点，此时只能从头开始遍历得到，所以选择B

在一个单链表HL中（HL为头结点指针），若要向表头插入一个由指针p指向的结点，则执行？

A． HL＝p; p->next＝HL;
B． p->next＝HL; HL＝p;
C． p->next＝HL; p＝HL;
D． p->next＝HL->next; HL->next＝p;

既然要在表头插入一个数据，也就是说要在第一个位置插入，那么根据我们之前讲解的链表的插入，只需要将头结点指向新的结点，再让新的结点指向原本的第一个结点即可，所以选择D

链表不具备的特点是？

A．可随机访问任一结点 B．插入删除不需要移动元素
C．不必事先估计存储空间 D．所需空间与其长度成正比

我们前面说了，链表由于是链式存储结构，无法直接访问到对应下标的元素，所以我们只能通过遍历去找到对应位置的元素，故选择A

双向链表和循环链表

前面我们介绍了单链表，通过这样的链式存储，我们不用再像顺序表那样一次性申请一段连续的空间，而是只需要单独为结点申请内存空间，同时在插入和删除的速度上也比顺序表轻松。不过有一个问题就是，如果我们想要操作某一个结点，比如删除或是插入，那么由于单链表的性质，我们只能先去找到它的前驱结点，才能进行。

为了解决这种查找前驱结点非常麻烦的问题，我们可以让结点不仅保存指向后续结点的指针，同时也保存指向前驱结点的指针：

这样我们无论在哪个结点，都能够快速找到对应的前驱结点，就很方便了，这样的链表我们成为双向链表（双链表）

这里我们也来尝试实现一下，首先定义好结构体：

typedef int E;

struct ListNode {
  E element;   //保存当前元素
  struct ListNode * next;   //指向下一个结点的指针
  struct ListNode * prev;   //指向上一个结点的指针
};

typedef struct ListNode * Node;

接着是初始化方法，在初始化时需要将前驱和后继都设置为NULL：

void initNode(Node node){
  node->next = node->prev = NULL;
}

int main() {
  struct ListNode head;
  initNode(&head);
}

接着是双向链表的插入操作，这就比单链表要麻烦一些了，我们先来分析一下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BiL0BdWn-1683974309668)(null)]

首先我们需要考虑后继结点，当新的结点插入之后，新的结点的后继结点就是原本在此位置上的结点，所以我们可以先将待插入结点的后继指针指向此位置上的结点：

由于是双向链表，所以我们需要将原本在此位置上的结点的前驱指针指向新的结点：

接着我们来处理一下前驱结点，首先将前驱结点的后继指针修改为新的结点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gOgUu8WP-1683974308972)(null)]

最后我们将新的结点的前驱指针指向前驱结点即可：

这样，我们就完成了双向链表中结点的插入操作，按照这个思路，我们来设计一下函数吧：

_Bool insertList(Node head, E element, int index){
  if(index < 1) return 0;   //跟单链表一样，还是先找到对应的位置
  while (--index) {
      head = head->next;
      if(head == NULL) return 0;
  }
  Node node = malloc(sizeof (struct ListNode));  //创建新的结点
  if(node == NULL) return 0;
	node->element = element;

  if(head->next) {   //首先处理后继结点，现在有两种情况，一种是后继结点不存在的情况，还有一种是后继结点存在的情况
      head->next->prev = node;   //如果存在则修改对应的两个指针
      node->next = head->next;
  } else {
      node->next = NULL;   //不存在直接将新结点的后继指针置为NULL
  }
  
  head->next = node;   //接着是前驱结点，直接操作就行
  node->prev = head;
  return 1;
}

这样，我们就编写好了双向链表的插入操作，来测试一下吧：

int main() {
  struct ListNode head;
  initNode(&head);
  for (int i = 0; i < 5; ++i)  //插5个元素吧
      insertList(&head, i * 100, i);

  Node node = &head;   //先来正向遍历一次
  do {
      node = node->next;
      printf("%d -> ", node->element);
  } while (node->next != NULL);

  printf("\n");   //再来反向遍历一次
  do {
      printf("%d -> ", node->element);
      node = node->prev;
  } while (node->prev != NULL);
}

可以看到结果没有问题：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yOccxlmr-1683974333996)(null)]

无论是正向遍历还是反向遍历，都可以正常完成，相比单链表的灵活度肯定是更大的，我们接着来看删除操作，其实删除操作也是差不多的方式：

我们只需将前驱结点和后继结点的指向修改即可：

接着直接删除对应的结点即可：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8hnmvkge-1683974335442)(null)]

现在我们就来编码吧：

_Bool deleteList(Node head, int index){
  if(index < 1) return 0;   //跟单链表一样，还是先找到对应的位置
  while (--index) {
      head = head->next;
      if(head == NULL) return 0;
  }
  if(head->next == NULL) return 0;

  Node tmp = head->next;  //先拿到待删除结点
  if(head->next->next) {   //这里有两种情况待删除结点存在后继结点或是不存在
      head->next->next->prev = head;
      head->next = head->next->next;   //按照上面分析的来
  }else{
      head->next = NULL;   //相当于删的是最后一个结点，所以直接后继为NULL就完事
  }
  free(tmp);   //最后释放已删除结点的内存
  return 1;
}

这样，我们就实现了双向链表的插入和删除操作，其他操作这里就不演示了。

接着我们再来简单认识一下另一种类型的链表，循环链表，这种链表实际上和前面我们讲的链表是一样的，但是它的最后一个结点，是与头结点相连的，双向链表和单向链表都可以做成这样的环形结构，我们这里以单链表为例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vBtTa2EE-1683974307487)(null)]

这种类型的链表实际上与普通链表的唯一区别就在于最后是否连接到头结点，因此循环链表支持从任意一个结点出发都可以到达任何的结点，而普通的链表则只能从头结点出发才能到达任意结点，同样也是为了更灵活而设计的。

链表练习题：

与单链表相比，双链表的优点之一是？

A．插入、删除操作更简单
B．可以进行随机访问
C．可以省略表头指针或表尾指针
D．顺序访问相邻结点更灵活

首先插入删除操作并没有更简单，反而更复杂了，随机访问肯定也是不行的，省略表头表尾指针实际上单链表也可以，所以直接冲D就完事了

非空的循环单链表head的尾结点（由p所指向）满足？

A．p->next == NULL B．p == NULL
C．p->next ==head D．p == head

前面我们说了，循环链表实际上唯一区别就是尾部的下一个结点会指向头部，所以这里选择C

若某表最常用的操作是在最后一个结点之后插入一个结点或删除最后一个结点，则采用什么存储方式最节省运算时间？

A．单链表 B．给出表头指针的单循环链表 C．双链表 D．带头结点的双循环链表

题干说明了常用的是在尾结点插入或删除尾结点，那么此时不仅需要快速找到最后一个结点，也需要快速找到最后一个结点的前驱结点，所以肯定是使用双向链表，为了快速找到尾结点，使用循环双向链表从头结点直接向前就能找到，所以选择D

如果对线性表的操作只有两种，即删除第一个元素，在最后一个元素的后面插入新元素，则最好使用？

A．只有表头指针没有表尾指针的循环单链表
B．只有表尾指针没有表头指针的循环单链表
C．非循环双链表
D．循环双链表

首先这里需要操作两个内容，一个是删除第一个元素，另一个是在最后插入新元素，所以A的话只有表头指针虽然循环但是还是得往后遍历才行，而B正好符合，因为循环链表的尾指针可以快速到达头结点，C不可能，D的话，循环双链表也可以，但是没有单链表节省空间，故B是最优解

特殊线性表

前面我们讲解的基础的线性表，通过使用线性表，我们就可以很方便地对数据进行管理了。这一部分，我们将继续认识一些特殊的线性表，它有着特别的规则，在特定场景有着很大的作用，也是考察的重点。

栈

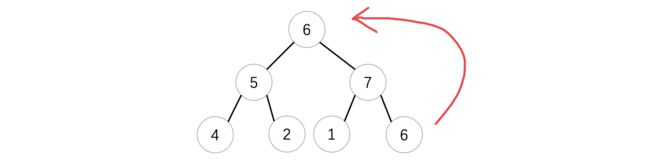
栈（也叫堆栈，Stack）是一种特殊的线性表，它只能在在表尾进行插入和删除操作，就像下面这样：

也就是说，我们只能在一端进行插入和删除，当我们依次插入1、2、3、4这四个元素后，连续进行四次删除操作，删除的顺序刚好相反：4、3、2、1，我们一般将其竖着看：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fIScP5rp-1683974307200)(null)]

底部称为栈底，顶部称为栈顶，所有的操作只能在栈顶进行，也就是说，被压在下方的元素，只能等待其上方的元素出栈之后才能取出，就像我们往箱子里里面放的书一样，因为只有一个口取出里面的物品，所以被压在下面的书只能等上面的书被拿出来之后才能取出，这就是栈的思想，它是一种先进后出的数据结构（FILO，First In, Last Out）

实现栈也是非常简单的，可以基于我们前面的顺序表或是链表，这里我们先使用顺序表来实现一下，这里我们需要实现两个新的操作：

pop：出栈操作，从栈顶取出一个元素。
push：入栈操作，向栈中压入一个新的元素。

首先还是按照我们的顺序表进行编写：

typedef int E;

struct Stack {
  E * array;
  int capacity;
  int top;   //这里使用top来表示当前的栈顶位置，存的是栈顶元素的下标
};

typedef struct Stack * ArrayStack;  //起个别名

接着我们需要编写一个初始化方法：

_Bool initStack(ArrayStack stack){
  stack->array = malloc(sizeof(E) * 10);
  if(stack->array == NULL) return 0;
  stack->capacity = 10;   //容量还是10
  stack->top = -1;   //由于栈内没有元素，那么栈顶默认就为-1
  return 1;
}

int main(){
  struct Stack stack;
  initStack(&stack);
}

接着就是栈的两个操作了，一个是入栈操作，一个是出栈操作：

_Bool pushStack(ArrayStack stack, E element){
  //入栈操作只需要给元素就可以，不需要index，因为只能从尾部入栈
}

由于入栈只能在尾部插入，所以就很好写了：

_Bool pushStack(ArrayStack stack, E element){
  stack->array[stack->top + 1] = element;   //直接设定栈顶元素
  stack->top++;   //栈顶top变量记得自增
  return 1;
}

我们来测试一下吧：

void printStack(ArrayStack stack){
  printf("| ");
  for (int i = 0; i < stack->top + 1; ++i) {
      printf("%d, ", stack->array[i]);
  }
  printf("\n");
}

int main(){
  struct Stack stack;
  initStack(&stack);
  for (int i = 0; i < 3; ++i) {
      pushStack(&stack, i*100);
  }
  printStack(&stack);
}

测试结果也是正确的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7oyfetkk-1683974331892)(null)]

可以看到，从栈底到栈顶一次是0、100、200，不过我们现在的push操作还不够完美，因为栈有可能塞满，所以要进行扩容处理：

_Bool pushStack(ArrayStack stack, E element){
  if(stack->top + 1 == stack->capacity) {  //栈顶+1如果等于容量的话，那么说明已经塞满了
      int newCapacity = stack->capacity + (stack->capacity >> 1);   //大体操作和顺序表一致
      E * newArray = realloc(stack->array, newCapacity * sizeof(E));
      if(newArray == NULL) return 0;
      stack->array = newArray;
      stack->capacity = newCapacity;
  }
  stack->array[stack->top + 1] = element;
  stack->top++;
  return 1;
}

这样我们的入栈操作就编写完成了，接着是出栈操作，出栈操作我们只需要将栈顶元素取出即可：

_Bool isEmpty(ArrayStack stack){   //在出栈之前，我们还需要使用isEmpty判断一下栈是否为空，空栈元素都没有出个毛
  return stack->top == -1;   
}

E popStack(ArrayStack stack){
  return stack->array[stack->top--];   //直接返回栈顶元素，注意多加一个自减操作
}

我们来测试一下吧：

int main(){
  struct Stack stack;
  initStack(&stack);
  for (int i = 0; i < 3; ++i) {
      pushStack(&stack, i*100);
  }
  printStack(&stack);
  while (!isEmpty(&stack)) {
      printf("%d ", popStack(&stack));   //将栈中所有元素依次出栈
  }
}

可以看到，出栈顺序和入栈顺序是完全相反的：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QXFWzAx4-1683974333705)(null)]

当然使用数组实现栈除了这种可以自己扩容的之外，也有固定大小的栈，当栈已满时，就无法再进行入栈操作了。

不过有些时候，栈的利用率可能会很低，这个时候我们可以将一个固定长度的数组共享给两个栈来使用：

数组的两头分别作为两个栈的栈底，当两个栈的栈顶指针相遇时（栈顶指针下标之差绝对值为1时），表示栈已满。通过这种方式，我们就可以将数组占用的空间更充分地使用，这样的栈我们称为共享栈。

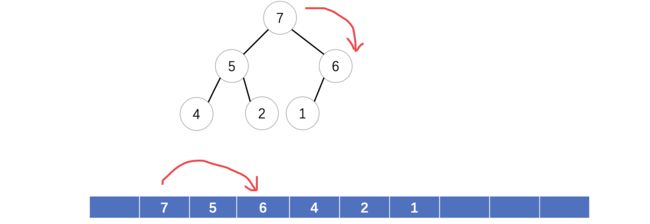
前面我们演示了使用顺序表实现栈，我们接着来看如何使用链表来实现栈，实际上使用链表会更加的方便，我们可以直接将头结点指向栈顶结点，而栈顶结点连接后续的栈内结点：

当有新的元素入栈，只需要在链表头部插入新的结点即可，我们来尝试编写一下：

typedef int E;

struct ListNode {
  E element;
  struct ListNode * next;
};

typedef struct ListNode * Node;

void initStack(Node head){
  head->next = NULL;
}

int main(){
  struct ListNode head;
  initStack(&head);
}

接着我们来编写一下入栈操作：

代码如下：

_Bool pushStack(Node head, E element){
  Node node = malloc(sizeof(struct ListNode));   //创建新的结点
  if(node == NULL) return 0;   //失败就返回0
  node->next = head->next;   //将当前结点的下一个设定为头结点的下一个
  node->element = element;   //设置元素
  head->next = node;   //将头结点的下一个设定为当前结点
  return 1;
}

我们来编写一个测试：

void printStack(Node head){
  printf("| ");
  head = head->next;
  while (head){
      printf("%d ", head->element);
      head = head->next;
  }
  printf("\n");
}

int main(){
  struct ListNode head;
  initStack(&head);
  for (int i = 0; i < 3; ++i) {
      pushStack(&head, i*100);
  }
  printStack(&head);
}

可以看到结果没有问题：

其实出栈也是同理，所以我们只需要将第一个元素移除即可：

_Bool isEmpty(Node head){
  return head->next == NULL;   //判断栈是否为空只需要看头结点下一个是否为NULL即可
}

E popStack(Node head){
  Node top = head->next;
  head->next = head->next->next;
  E e = top->element;
  free(top);  //别忘了释放结点的内存
  return e;   //返回出栈元素
}

这里我们来测试一下：

int main(){
  struct ListNode head;
  initStack(&head);
  for (int i = 0; i < 3; ++i) {
      pushStack(&head, i*100);
  }
  printStack(&head);
  while (!isEmpty(&head)) {
      printf("%d ", popStack(&head));   //将栈中所有元素依次出栈
  }
}

实际上无论使用链表还是顺序表，都可以很轻松地实现栈，因为栈的插入和删除操作很特殊。

栈练习题：

若进栈序列为1，2，3，4，则不可能得到的出栈序列是？

A. 3，2，1，4 B. 3，2，4，1
C. 4，2，3，1 D. 2，3，4，1

注意进栈并不一定会一次性全部进栈，可能会出现边进边出的情况，所以出栈的顺序可能有很多种情况，首先来看A，第一个出栈的是3，那么按照顺序，说明前面一定入栈了2、1，在出栈时4还没有入栈，然后是2、1最后是4，没有问题。接着是B，跟前面的A一样，不过这次是先出站3、2，而1留在栈中，接着4入栈，然后再让4、1出栈，也是正确的。然后是C，首先是4出栈，那么说明前三个一定都入栈了，而此时却紧接着的一定是3，而这里是2，错误。所以选择C

假设有5个整数以1、2、3、4、5的顺序被压入堆栈，且出栈顺序为3、5、4、2、1，那么栈大小至少为？

A.2
B.3
C.4
D.5

首先我们分析一下，第一个出栈的元素为3，那么也就是说前面的1、2都在栈内，所以大小至少为3，然后是5，那么说明此时栈内为1、2、4，算是出栈的5，那么至少需要的大小就是4了，所以选择C

队列

前面我们学习了栈，栈中元素只能栈顶出入，它是一种特殊的线性表，同样的，队列（Queue）也是一种特殊的线性表。

就像我们在超市、食堂需要排队一样，我们总是排成一列，先到的人就排在前面，后来的人就排在后面，越前面的人越先完成任务，这就是队列，队列有队头和队尾：

秉承先来后到的原则，队列中的元素只能从队尾进入，只能从队首出去，也就是说，入队顺序为1、2、3、4，那么出队顺序也一定是1、2、3、4，所以队列是一种先进先出（FIFO，First In, First Out）的数据结构。

想要实现队列也是很简单的，也可以通过两种线性表来实现，我们先来看看使用顺序表如何实现队列，假设一开始的时候队列中有0个元素，队首和队尾一般都初始都是-1这个位置：

此时有新的元素入队了，队尾向后移动一格（+1），然后在所指向位置插入新的元素：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pM3MJbJ5-1683974309250)(null)]

之后都是同样的方式进行插入，队尾会一直向后移动：

现在我们想要执行出队操作了，那么需要将队首向后移动一格，然后删除队首指向的元素：

看起来设计的还挺不错的，不过这样有一个问题，这个队列是一次性的，如果队列经过反复出队入队操作，那么最后指针会直接指向数组的最后，如果我们延长数组的话，也不是一个办法，不可能无限制的延伸下去吧？所以一般我们采用循环队列的形式，来实现重复使用一个数组（不过就没办法扩容了，大小是固定的）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8SZhL0Wq-1683974331602)(null)]

我们可以在移动队首队尾指针时，考虑循环的问题，也就是说如果到达了数组尽头，那么就直接从数组的前面重新开始计算，这样就相当于逻辑上都循环了，队首和队尾指针在一开始的时候都指向同一个位置，每入队一个新的元素，依然是先让队尾后移一位，在所指向位置插入元素，出队同理。

不过这样还是有问题，既然是循环的，那么怎么判断队列是否已满呢？

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-CxtJeZqr-1683974334568)(null)]

由于队首指针和队尾指针重合时表示队列为空，所以我们只能舍弃一个存储单元，当队尾距离队首一个单元的时候，表示队列已满。

好了，现在理论讲解完毕，我们可以开始编写代码了：

typedef int E;

struct Queue {
  E * array;
  int capacity;   //数组容量
  int rear, front;   //队尾、队首指针
};

typedef struct Queue * ArrayQueue;

接着我们来对其进行初始化：

_Bool initQueue(ArrayQueue queue){
  queue->array = malloc(sizeof(E) * 10);
  if(queue->array == NULL) return 0;
  queue->capacity = 10;
  queue->front = queue->rear = 0;   //默认情况下队首和队尾都指向0的位置
  return 1;
}

int main(){
  struct Queue queue;
  initQueue(&queue);   
}

接着我们来编写一下入队操作：

_Bool offerQueue(ArrayQueue queue, E element){
  if((queue->rear + 1) % queue->capacity == queue->front)   //先判断队列是否已满，如果队尾下一个就是队首，那么说明已满
      return 0;
  queue->rear = (queue->rear + 1) % queue->capacity;   //队尾先向前移动一位，注意取余计算才能实现循环
  queue->array[queue->rear] = element;   //在新的位置插入元素
  return 1;
}

我们来测试一下：

void printQueue(ArrayQueue queue){
  printf("<<< ");
  int i = queue->front;   //遍历队列需要从队首开始
  do {
      i = (i + 1) % queue->capacity;   //先向后循环移动
      printf("%d ", queue->array[i]);  //然后打印当前位置上的元素
  } while (i != queue->rear);   //当到达队尾时，结束
  printf("<<<\n");
}

int main(){
  struct Queue queue;
  initQueue(&queue);
  for (int i = 0; i < 5; ++i) {
      offerQueue(&queue, i * 100);
  }
  printQueue(&queue);
}

最后结果如下：

我们接着来看出队操作：

_Bool isEmpty(ArrayQueue queue){   //在出队之前需要先看看容量是否足够
  return queue->rear == queue->front;
}

E pollQueue(ArrayQueue queue){
  queue->front = (queue->front + 1) % queue->capacity;   //先将队首指针后移
  return queue->array[queue->front];   //出队，完事
}

我们来测试一下吧：

int main(){
  struct Queue queue;
  initQueue(&queue);
  for (int i = 0; i < 5; ++i) {
      offerQueue(&queue, i * 100);
  }
  printQueue(&queue);
  while (!isEmpty(&queue)) {
      printf("%d ", pollQueue(&queue));
  }
}

我们来看看结果：

可以看到，队列是先进先出的，我们是以什么顺序放入队列中，那么出来的就是是什么顺序。

同样的，队列也可以使用链表来实现，并且使用链表的话就不需要关心容量之类的问题了，会更加灵活一些：

注意我们需要同时保存队首和队尾两个指针，因为是单链表，所以队首需要存放指向头结点的指针，因为需要的是前驱结点，而队尾则直接是指向尾结点的指针即可，后面只需要直接在后面拼接就行。

当有新的元素入队时，只需要拼在队尾就行了，同时队尾指针也要后移一位：

出队时，只需要移除队首指向的下一个元素即可：

那么我们就按照这个思路，来编写一下代码吧：

typedef int E;

struct LNode {
  E element;
  struct LNode * next;
};

typedef struct LNode * Node;

struct Queue{
  Node front, rear;
};

typedef struct Queue * LinkedQueue;   //因为要存储首位两个指针，所以这里封装一个新的结构体吧

接着是初始化，初始化的时候，需要把头结点先创建出来：

_Bool initQueue(LinkedQueue queue){
  Node node = malloc(sizeof(struct LNode));
  if(node == NULL) return 0;
  queue->front = queue->rear = node;   //一开始两个指针都是指向头结点的，表示队列为空
  return 1;
}

int main(){
  struct Queue queue;
  initQueue(&queue);
}

首先是入队操作，入队其实直接在后面插入新的结点就行了：

_Bool offerQueue(LinkedQueue queue, E element){
  Node node = malloc(sizeof(struct LNode));
  if(node == NULL) return 0;
  node->element = element;
  queue->rear->next = node;   //先让尾结点的下一个指向新的结点
  queue->rear = node;   //然后让队尾指针指向新的尾结点
  return 1;
}

我们来测试一下看看：

void printQueue(LinkedQueue queue){
  printf("<<< ");
  Node node = queue->front->next;
  while (node) {
      printf("%d ", node->element);  //链表就简单多了，直接挨个遍历就完事
      node = node->next;
  }
  printf("<<<\n");
}

int main(){
  struct Queue queue;
  initQueue(&queue);
  for (int i = 0; i < 5; ++i) {
      offerQueue(&queue, i*100);
  }
  printQueue(&queue);
}

测试结果如下：

接着是出队操作，出队操作要相对麻烦一点：

E pollQueue(LinkedQueue queue){
  E e = queue->front->next->element;
  Node node = queue->front->next;
  queue->front->next = queue->front->next->next;  //直接让头结点指向下下个结点
  if(queue->rear == node) queue->rear = queue->front;   //如果队尾就是待出队的结点，那么队尾回到队首位置上
  free(node);   //释放内存
  return e;
}

这样，我们就编写好了：

int main(){
  struct Queue queue;
  initQueue(&queue);
  for (int i = 0; i < 5; ++i) {
      offerQueue(&queue, i*100);
  }
  printQueue(&queue);
  while (!isEmpty(&queue)){
      printf("%d ", pollQueue(&queue));
  }
}

测试结果如下：

效果和前面的数组实现是一样的，只不过使用链表会更加灵活一些。

队列练习题：

使用链表方式存储的队列，在进行出队操作时需要？

A. 仅修改头结点指向 B. 仅修改尾指针 C. 头结点指向、尾指针都要修改 D. 头结点指向、尾指针可能都要修改

首先出队肯定是要动头结点指向的，但是不一定需要动尾指针，因为只有当尾指针指向的是待出队的元素时才需要，因为执行后队列就为空了，所以需要将队尾指针移回头结点处，选择D

引起循环队列队头位置发生变化的操作是？

A. 出队

B. 入队

C. 获取队头元素

D. 获取队尾元素

这个题还是很简单的，因为只有出队操作才会使得队头位置后移，所以选择A

算法实战

欢迎来到线性结构篇算法实战，这一部分我们将从算法相关题目上下手，解决实际问题，其中链表作为重点考察项目。

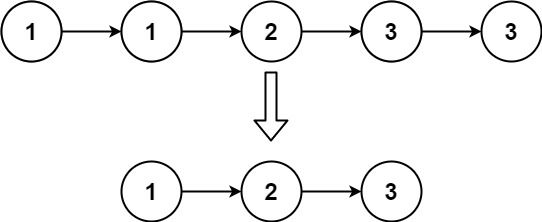
（简单）删除链表中重复元素

本题来自LeetCode：83. 删除排序链表中的重复元素

给定一个已排序的链表的头 head（注意是无头结点的链表，上来第一个结点就是存放第一个元素），删除所有重复的元素，使每个元素只出现一次。返回已排序的链表。

示例 1：

输入：head = [1,1,2]
输出：[1,2]

示例 2：

输入：head = [1,1,2,3,3]
输出：[1,2,3]

这道题实际上比较简单，只是考察各位小伙伴对于链表数据结构的掌握程度，我们只需要牢牢记住如何对链表中的元素进行删除操作就能轻松解决这道题了。

struct ListNode* deleteDuplicates(struct ListNode* head){
  if(head == NULL) return head;  //首先如果进来的就是NULL，那就不用再浪费时间了
  struct ListNode * node = head;  //这里用一个指针来表示当前所指向的结点
  while (node->next != NULL) {   //如果结点的下一个为空，就没必要再判断了，否则不断进行判断
      if(node->next->val == node->val) {  //如果下一个节点跟当前节点值一样，那么删除下一个节点
          node->next = node->next->next;
      } else {
          node = node->next;   //否则继续从下一个节点开始向后判断
      }
  }
  return head;   //最后原样返回头结点
}

（简单）反转链表

本题来自LeetCode：206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PTrPP4Hi-1683974308113)(null)]

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

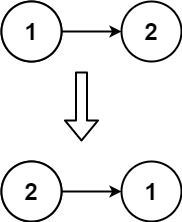
输入：head = [1,2]
输出：[2,1]

这道题依然是考察各位小伙伴对于链表相关操作的掌握程度，我们如何才能将一个链表的顺序进行反转，关键就在于如何修改每个节点的指针指向。

struct ListNode* reverseList(struct ListNode* head){
  struct ListNode * newHead = NULL, * tmp;   //创建一个指针存放新的头结点（注意默认要为NULL），和一个中间暂存指针
  while (head != NULL) {   //这里利用head不断向后遍历，来依次修改每个结点的指向
      tmp = head;   //先暂存当前结点
      head = head->next;  //head可以先后移了
      tmp->next = newHead;   //将暂存节点的下一个节点，指向前一个结点
      newHead = tmp;   //最后新的头结点就是tmp所指向结点，这样循环操作直到结束
  }
  return newHead;  //最后返回新的结点即可
}

（中等）旋转链表

本题来自LeetCode：61. 旋转链表

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

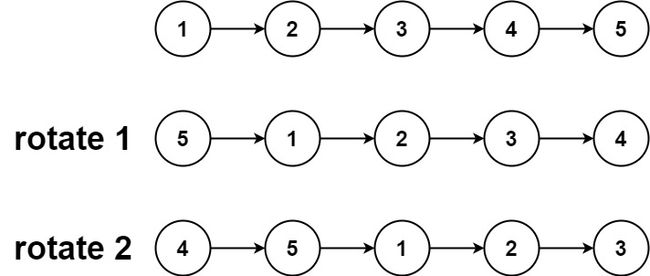
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

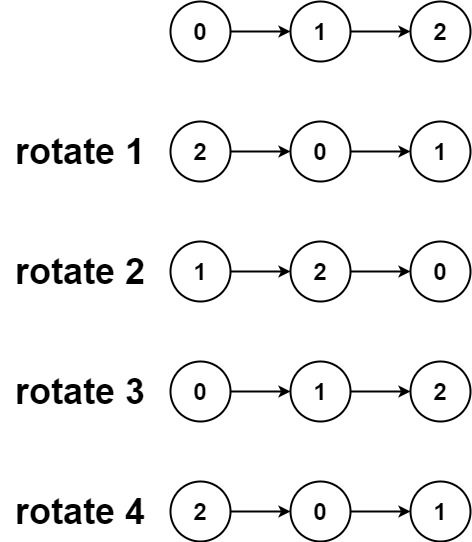
输入：head = [0,1,2], k = 4
输出：[2,0,1]

这道题需要我们进行一些思考了，首先我们要知道，在经过旋转之后最终的头结点是哪一个，在知道后，这道题就很简单了，我们只需要断掉对应头结点的指针即可，最后返回头结点，就是旋转之后的链表了。

struct ListNode* rotateRight(struct ListNode* head, int k){
  if(head == NULL || k == 0) return head;   //如果给进来的链表是空的，或者说k为0，那么就没必要再继续了
  struct ListNode * node = head;
  int len = 1;
  while (node->next) {   //先来算一波链表的长度
      node = node->next;
      len++;
  }
	if(k == len) return head;   //如果len和k长度一样，那也没必要继续了

  node->next = head;   //将链表连起来变成循环的，一会再切割
  int index = len - k % len;  //计算头结点最终位置

	node = head;
  while (--index) node = node->next;
  head = node->next;    //找到新的头结点
  node->next = NULL;   //切断尾部与头部
  return head;  //返回新的头结点
}

（简单）有效的括号

本题来自LeetCode：20. 有效的括号

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

输入：s = “()”
输出：true

示例 2：

输入：s = “()[]{}”
输出：true

示例 3：

输入：s = “(]”
输出：false

示例 4：

输入：s = “([)]”
输出：false

示例 5：

输入：s = “{[]}”
输出：true

题干很明确，就是需要我们去对这些括号完成匹配，如果给定字符串中的括号无法完成一一匹配的话，那么就表示匹配失败。实际上这种问题我们就可以利用前面学习的栈这种数据结构来解决，我们可以将所有括号的左半部分放入栈中，当遇到右半部分时，进行匹配，如果匹配失败，那么就失败，如果匹配成功，那么就消耗一个左半部分，直到括号消耗完毕。

#include 
#include 
#include 

typedef char E;

struct LNode {
  E element;
  struct LNode * next;
};

typedef struct LNode * Node;

void initStack(Node head){
  head->next = NULL;
}

_Bool pushStack(Node head, E element){
  Node node = malloc(sizeof(struct LNode));
  if(node == NULL) return 0;
  node->next = head->next;
  node->element = element;
  head->next = node;
  return 1;
}

_Bool isEmpty(Node head){
  return head->next == NULL;
}

E popStack(Node head){
  Node top = head->next;
  head->next = head->next->next;
  E e = top->element;
  free(top);
  return e;
}

bool isValid(char * s){
  unsigned long len = strlen(s);
  if(len % 2 == 1) return false;  //如果长度不是偶数，那么一定不能成功匹配
  struct LNode head;
  initStack(&head);
  for (int i = 0; i < len; ++i) {
      char c = s[i];
      if(c == '(' || c == '[' || c == '{') {
          pushStack(&head, c);
      }else {
          if(isEmpty(&head)) return false;
          if(c == ')') {
              if(popStack(&head) != '(') return false;
          } else if(c == ']') {
              if(popStack(&head) != '[') return false;
          } else {
              if(popStack(&head) != '{') return false;
          }
      }
  }
  return isEmpty(&head);
}

一般遇到括号匹配问题、算式计算问题，都可以使用栈这种数据结构来轻松解决。当然使用C语言太过原始，像Java、C++这些语言一般系统库都会直接提供栈的实现类，所以我们在打比赛时，可以尽量选择这些方便的语言，能节省不少时间。

（简单）第 k 个缺失的正整数

本题来自LeetCode：1539. 第 k 个缺失的正整数

给你一个严格升序排列的正整数数组 arr 和一个整数 k 。

请你找到这个数组里第 k 个缺失的正整数。

示例 1：

输入：arr = [2,3,4,7,11], k = 5
输出：9
解释：缺失的正整数包括 [1,5,6,8,9,10,12,13,…] 。第 5 个缺失的正整数为 9 。

示例 2：

输入：arr = [1,2,3,4], k = 2
输出：6
解释：缺失的正整数包括 [5,6,7,…] 。第 2 个缺失的正整数为 6 。

实际上这种问题，我们第一个能够想到的就是直接通过遍历挨个寻找，从头开始一个一个找，总能找到第K个吧？我们可以很轻松地得到如下的代码：

int findKthPositive(int* arr, int arrSize, int k){
  int j = 1, i = 0;   //直接从第一个元素开始挨个找
  while (i < arrSize) {
      if(arr[i] != j) {
          if(--k == 0) return j;   //发现不相等时，相当于找到了一个数，k自减，如果自减后为0，那么说明已经找到第K个了，直接返回对应的j
      } else{
          i++;  //相等的话就继续看下一个
      }
      j++;   //每一轮j自增，表示下一轮应该按顺序匹配的数
  }
  return j + k - 1;   //如果遍历完了都还没找到，那就按顺序直接算出下一个
}

不过这样的效率并不高，如果这个数组特别长的话，那么我们总不可能还是挨个看吧？这样的遍历查找算法的时间复杂度为 $O (n)$ ，那么有没有更好的算法能够解决这种问题呢？

既然这个数组是有序的，那么我们不妨直接采用二分搜索的思想，通过使用二分搜索，我们就可以更快速地找到对应的位置，但是有一个问题，我们怎么知道二分搜索找到的数，是不是第N个数呢？实际上也很简单，通过规律我们不难发现，如果某个位置上的数不匹配，那么被跳过的数k一定满足：
$k = a rr [i] - i - 1$
所以，我们只需要找到一个大于等于k的位置即可，并且要尽可能的接近，在找到之后，再根据公式去寻找即可：

int findKthPositive(int *arr, int arrSize, int k) {
  if (arr[0] > k) return k;
  
  int l = 0, r = arrSize;
  while (l < r) {
      int mid = (l + r) / 2;
      if (arr[mid] - mid - 1 >= k) {
          r = mid;
      } else {
          l = mid + 1;
      }
  }

  return k - (arr[l - 1] - (l - 1) - 1) + arr[l - 1];
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gK58iL0D-1683974334286)(null)]

树形结构篇

前面我们学习了线性相关的数据结构，了解了顺序表和链表两种类型，我们接着来看树形结构。这一章会更加考验各位小伙伴的数学功底以及逻辑思维，难度会更大一些。

树与森林

树是一种全新的数据结构，它就像一棵树的树枝一样，不断延伸。

树结构介绍

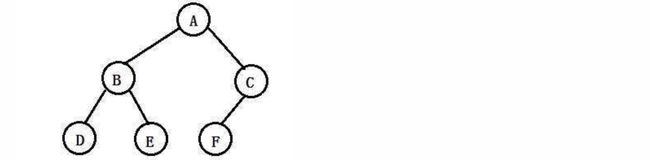
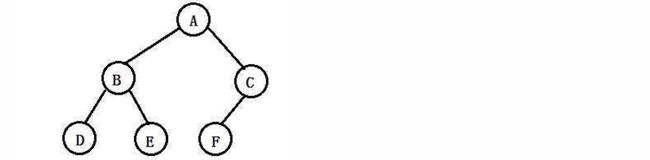
一棵树就像下面这样连接：

可以看到，现在一个结点下面可能会连接多个节点，并不断延伸，就像树枝一样，每个结点都有可能是一个分支点，延伸出多个分支，从位于最上方的结点开始不断向下，而这种数据结构，我们就称为树（Tree）注意分支只能向后单独延伸，之后就分道扬镳了，不能与其他分支上的结点相交！

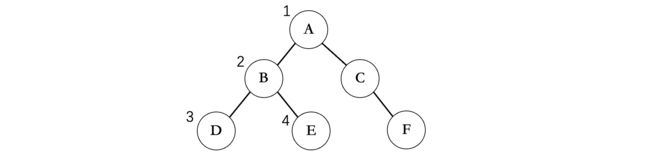
我们一般称位于最上方的结点为树的根结点（Root）因为整棵树正是从这里开始延伸出去的。
每个结点连接的子结点数目（分支的数目），我们称为结点的度（Degree），而各个结点度的最大值称为树的度。
每个结点延伸下去的下一个结点都可以称为一棵子树（SubTree）比如结点B及其之后延伸的所有分支合在一起，就是一棵A的子树。
每个结点的层次（Level）按照从上往下的顺序，树的根结点为1，每向下一层+1，比如G的层次就是3，整棵树中所有结点的最大层次，就是这颗树的深度（Depth），比如上面这棵树的深度为4，因为最大层次就是4。

由于整棵树错综复杂，所以说我们需要先规定一下结点之间的称呼，就像族谱那样：

与当前结点直接向下相连的结点，我们称为子结点（Child），比如B、C、D结点，都是A的子结点，就像族谱中的父子关系一样，下一代一定是子女，相反的，那么A就是B、C、D的父结点（Parent），也可以叫双亲结点。
如果某个节点没有任何的子结点（结点度为0时）那么我们称这个结点为叶子结点（因为已经到头了，后面没有分支了，这时就该树枝上长叶子了那样）比如K、L、F、G、M、I、J结点，都是叶子结点。
如果两个结点的父结点是同一个，那么称这两个节点为兄弟结点（Sibling）比如B和C就是兄弟结点，因为都是A的孩子。
从根结点开始一直到某个结点的整条路径的所有结点，都是这个结点的祖先结点（Ancestor）比如L的祖先结点就是A、B、E

那么在了解了树的相关称呼之后，相信各位就应该对树有了一定的了解，虽然概念比较多，但是还请各位一定记住，不然后面就容易听懵。

森林

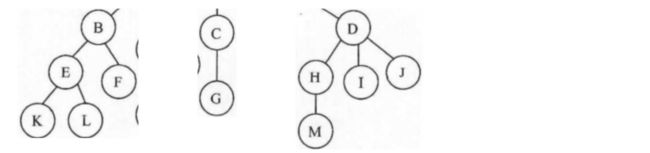
森林其实很好理解，一片森林肯定是是由很多棵树构成的，比如下面的三棵树：

它们共同组成了一片森林，因此，m（m≥0）棵树的集合我们称为森林（Forest）

二叉树

前面我们给大家介绍了树的概念，而我们本章需要着重讨论的是二叉树（Binary Tree）它是一种特殊的树，它的度最大只能为2，所以我们称其为二叉树，一棵二叉树大概长这样：

并且二叉树任何结点的子树是有左右之分的，不能颠倒顺序，比如A结点左边的子树，称为左子树，右边的子树称为右子树。

二叉树有5种基本形态，分别是：

满二叉树和完全二叉树

当然，对于某些二叉树我们有特别的称呼，比如，在一棵二叉树中，所有分支结点都存在左子树和右子树，且叶子结点都在同一层：

这样的二叉树我们称为满二叉树，可以看到整棵树都是很饱满的，没有出现任何度为1的结点，当然，还有一种特殊情况：

可以看到只有最后一层有空缺，并且所有的叶子结点是按照从左往右的顺序排列的，这样的二叉树我们一般称其为完全二叉树，所以，一棵满二叉树，一定是一棵完全二叉树。

树和森林的转换

二叉树和树、森林之间是可以相互转换的。

我们可以使用下面的规律将一棵普通的树转换为一棵二叉树：

最左边孩子结点 -> 左子树结点（左孩子）
兄弟结点 -> 右子树结点（右孩子）

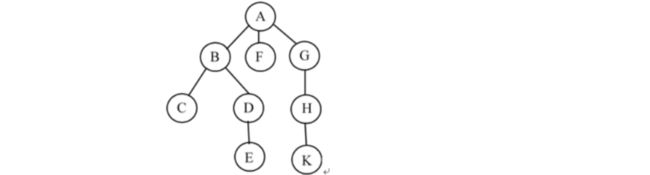
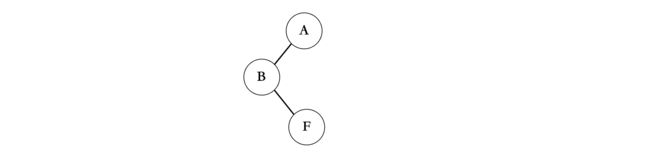
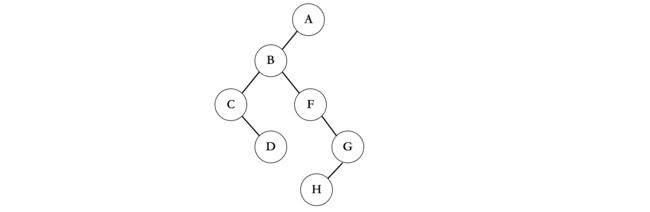
我们以下面的这棵树为例：

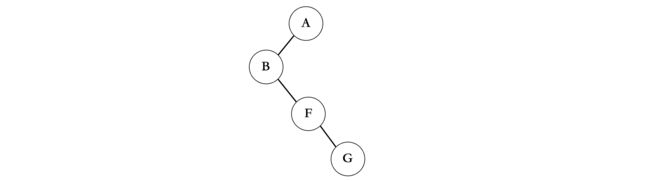
我们优先从左边开始看，B、F、G都是A的子结点，根据上面的规律，我们将B作为左子树：

接着继续从左往右看，由于F是B的兄弟结点，那么根据规律，F作为B的右子树：

接着是G，G是F的兄弟结点，那么G继续作为F的右子树：

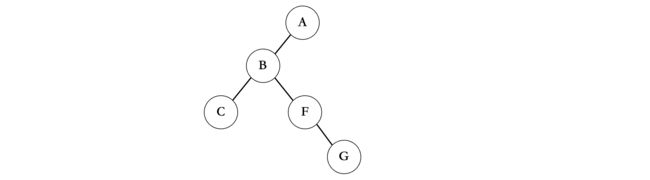
我们接着来看第三排，依然是从左往右，C是B的子节点，所以C作为B的左子树：

接着，D是C的兄弟节点，那么D就作为C的右子树了：

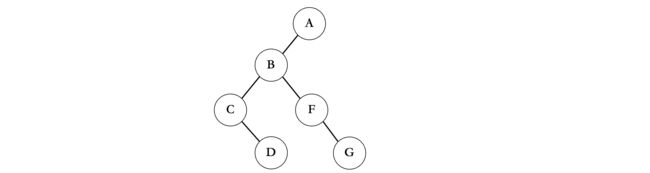
此时还有一个H结点，它是G的子结点，所以直接作为G的左子树：

现在只剩下最后一排了，E是D的子结点，K是H的子结点，所以最后就像这样了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cfXGrmIy-1683974297356)(https://s2.loli.net/2022/08/06/6JxYP2CXSyZdGa4.png)]

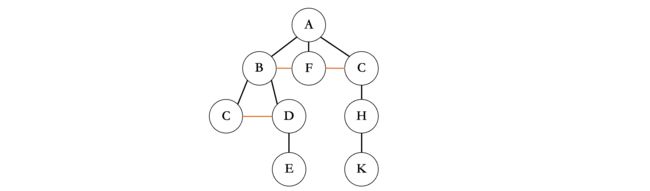
按照规律，我们就将一棵树转换为了二叉树。当然还有一种更简单的方法，我们可以直接将所有的兄弟结点连起来（橙色横线）：

接着擦掉所有结点除了最左边结点以外的连线：

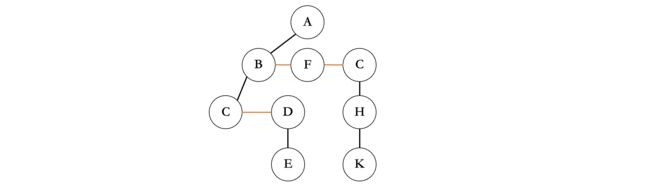
所有的黑色连线偏向左边，橙色连线偏向右边：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GlHYroVq-1683974297357)(https://s2.loli.net/2022/08/07/yzA2uLqhYDnbZcJ.png)]

效果是一样的，这两种方式都可以，你觉得哪一种简单就使用哪一种就行了。我们会发现，无论一棵树长成啥样，转换为二叉树后，根节点一定没有右子树。

**思考：**那二叉树咋变回普通的树呢？实际上我们只需要反推回去就行了。

那么森林呢，森林如何转换为一棵二叉树呢？其实很简单：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B9Kl3Rwh-1683974297358)(https://s2.loli.net/2022/08/08/QCIaYTcEv2NO47G.png)]

首先我们还是按照二叉树转换为树的规则，将森林中所有树转换为二叉树，接着我们只需要依次连接即可：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XK8ImfMm-1683974297358)(https://s2.loli.net/2022/08/08/O3xnhv85WLPzJpq.png)]

注意连接每一棵树的时候，一律从根结点的右边开始，不断向右连接。

我们发现，相比树转换为二叉树，森林转换为二叉树之后，根节点就存在右子树了，右子树连接的都是森林中其他的树。

**思考：**现在有一棵二叉树，我们想要转回去，我们怎么知道到底是将其转换为森林还是转换为树呢？

二叉树的性质

由于二叉树结构特殊，我们可以总结出以下的五个性质：

**性质一：**对于一棵二叉树，第i层的最大结点数量为 $2^{i-1} $ 个，比如二叉树的第一层只有一个根结点，也就是 $2^0 = 1$ ，而二叉树的第三层可以有 $2^2 = 4$ 个结点。
**性质二：**对于一棵深度为k的二叉树，可以具有的最大结点数量为：
$n = 2^0 + 2^1 + 2^2 + ... + 2^{k-1}$
我们发现，实际上每一层的结点数量，组成了一个等比数列，公比q为2，结合等比数列求和公式，我们可以将其简化为：
$S_n = \frac {a_1 \times (1 - q^n)} {1 - q} = \frac {1 \times (1 - 2^k)} {1 - 2} = - (1 - 2^k) = 2^k - 1$
所以一棵深度为k的二叉树最大结点数量为 $n = 2^k - 1$ ，顺便得出，结点的边数为 $E = n - 1$ 。
性质三：假设一棵二叉树中度为0、1、2的结点数量分别为 $n_0$ 、 $n_1$ 、 $n_2$ ，由于一棵二叉树中只有这三种类型的结点，那么可以直接得到结点总数：
$n = n_0 + n_1 + n_2$
我们不妨换一个思路，我们从二叉树的边数上考虑，因为每个结点有且仅有一条边与其父结点相连，那么边数之和就可以表示为：
$E = n_1 + 2n_2$
度为1的结点有一条边，度为2的结点有两条边，度为0的结点没有，加在一起就是整棵二叉树的边数之和，结合我们在性质二中推导的结果，可以得到另一种计算结点总数的方式：
$E = n - 1 = n_1 + 2n_2$

$n = n_1 + 2n_2 + 1$

再结合我们第一个公式：
$n = n_0 + n_1 + n_2 = n_1 + 2n_2 + 1$
综上，对于任何一棵二叉树，如果其叶子结点个数为 $n_0$ ，度为2的结点个数为 $n_2$ ，那么两者满足以下公式：
$n_0 = n_2 + 1$
（性质三的推导过程比较复杂，如果觉得麻烦推荐直接记忆）
**性质四：**完全二叉树除了最后一层有空缺外，其他层数都是饱满的，假设这棵二叉树为满二叉树，那么根据我们前面得到的性质，假设层数为k，那么结点数量为： $n = 2^k - 1$ ，根据完全二叉树的性质，最后一层可以满可以不满，那么一棵完全二叉树结点数n满足：
$2^{k-1} - 1 < n <= 2^k - 1$
因为n肯定是一个整数，那么可以写为：
$2^{k - 1} <= n <= 2^k - 1$
现在我们只看左边的不等式，我们对不等式两边同时取对数，得到：
$k - 1 <= log_2n$
综上所述，一棵具有n个结点的完全二叉树深度为 $\lfloor log_2n \rfloor + 1$ 。

（性质四的推导过程比较复杂，如果觉得麻烦推荐直接记忆）
**性质五：**一颗有n个结点的完全二叉树，由性质四得到深度为 $\lfloor log_2n \rfloor + 1$ 现在对于任意一个结点i，结点的顺序为从上往下，从左往右：
- 对于一个拥有左右孩子的结点来说，其左孩子为2i，右孩子为2i + 1。
- 如果i = 1，那么此结点为二叉树的根结点，如果i > 1，那么其父结点就是 $\lfloor i/2 \rfloor$ ，比如第3个结点的父结点为第1个节点，也就是根结点。
- 如果2i > n，则结点i没有左孩子，比如下面图中的二叉树，n为5，假设此时i = 3，那么2i = 6 > n = 5 说明第三个结点没有左子树。
- 如果2i + 1 > n，则结点i没有右孩子。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DEEMc3Pn-1683974297359)(https://s2.loli.net/2022/08/05/uan6A3ZRLykt289.png)]

以上五条二叉树的性质一般是笔试重点内容，还请务必牢记，如果觉得推导过程比较麻烦，推荐直接记忆结论。

二叉树练习题：

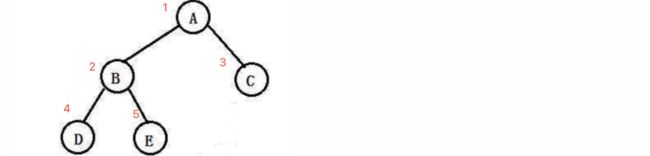
由三个结点可以构造出多少种不同的二叉树？

这个问题我们可以直接手画得到结果，一共是五种，当然，如果要求N个结点的话，可以利用动态规划求解，如果这道题是求N个结点可以构造多少二叉树，我们可以分析一下：
- 假设现在只有一个结点或者没有结点，那么只有一种， $h (0) = h (1) = 1$
- 假设现在有两个结点，那么其中一个拿来做根结点，剩下这一个可以左边可以右边，要么左边零个结点右边一个结点，要么左边一个结点右边零个结点，所以说 $h (2) = h (1) \times h (0) + h (0) \times h (1) = 2$
- 假设现在有三个结点，那么依然是其中一个拿来做根节点，剩下的两个结点情况就多了，要么两个都在左边，两个都在右边，或者一边一个，所以说 $h (3) = h (2) \times h (0) + h (1) \times h (1) + h (0) \times h (2)$
我们发现，它是非常有规律的，N每+1，项数多一项，所以我们只需要按照规律把所有情况的结果相加就行了，我们按照上面推导的结果，编写代码：
```
int main(){
    int size;
    scanf("%d", &size);   //读取需要求的N
    int dp[size + 1];
    dp[0] = dp[1] = 1;   //没有结点或是只有一个结点直接得到1
    for (int i = 2; i <= size; ++i) {
        dp[i] = 0;   //一开始先等于0再说
        for (int j = 0; j < i; ++j) {   //内层循环是为了计算所有情况，比如i等于3，那么就从j = 0开始，计算dp[0]和dp[2]的结果，再计算dp[1]和dp[1]...
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    printf("%d", dp[size]);   //最后计算的结果就是N个结点构造的二叉树数量了
}
```
成功得到结果，当然，实际上我们根据这个规律，还可以将其进一步简化，求出的结果序列为：1, 1, 2, 5, 14, 42, 132…，这种类型的数列我们称为卡特兰数，以中国蒙古族数学家明安图 (1692-1763)和比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名，它的通项公式为：
$C_n = \frac {1} {n + 1}C^n_{2n} = \frac {1} {n + 1} \times \frac {(2n)!} {n!\times(2n - n)!} = \frac {(2n)!} {n!\times (n + 1)!}$
所以说不需要动态规划了，直接一个算式解决问题：
```
int factorial(int n){
    int res = 1;
    for (int i = 2; i <= n; ++i) res *= i;
    return res;
}

int main(){
    int n;
    scanf("%d", &n);
    printf("%d", factorial(2*n) / (factorial(n) * factorial(n + 1)));
}
```
只不过这里用的是int，运算过程中如果数字太大的话就没办法了
一棵完全二叉树有1001个结点，其中叶子结点的个数为？

既然是完全二叉树，那么最下面这一排肯定是按顺序排的，并且上面各层应该是排满了的，那么我们先求出层数，根据性质四：
$\lfloor log_2n \rfloor + 1 = 9 + 1 = 10$
所以此二叉树的层数为10，也就是说上面9层都是满满当当的，最后一层不满，那么根据性质二，我们求出前9层的结点数：
$n = 2^k - 1 = 511$
那么剩下的结点就都是第十层的了，得到第十层所有叶子结点数量 $ = 1001 - 511 = 490$，因为第十层并不满，剩下的叶子第九层也有，所以最后我们还需要求出第九层的叶子结点数量，先计算第九层的所有结点数量：
$n = 2^{i - 1}=256$
接着我们需要去掉那些第九层度为一和度为二的结点，其实只需要让第十层都叶子结点除以2就行了：
$n = (490 + 1) /2 = 245$
注意在除的时候+1，因为有可能会出现一个度为1的结点，此时也需要剔除，所以说+1变成偶数这样才可以正确得到结果。最后剔除这些结点，得到最终结果：
$n_0 = 256 - 245 + 490 = 501$
所以这道题的答案为501。
深度为h的满m叉树的第k层有多少个结点？

这道题只是看着复杂，但是实际上我们把之前推导都公式带进来就行了。但是注意，难点在于，这道题给的是满m叉树，而不是满二叉树，满二叉树根据性质一我们已经知道：
$n = 2^{i-1}$
那m叉树呢？实际上也是同理的，我们以三叉树为例，每向下一层，就划分三个孩子结点出来：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ntDgvvVe-1683974297360)(https://s2.loli.net/2022/08/08/XvH4At8Q93nkFIR.png)]

每一层的最大结点数依次为：1、3、9、27…

我们发现，实际上每一层的最大结点数，正好是3的次方，所以说无论多少叉树，实际上变化的就是底数而已，所以说深度为h（h在这里没卵用，障眼法罢了）的满m叉树第k层的结点数：
$n = m^{k-1}$
一棵有1025个结点的二叉树的层数k的取值范围是？

这个问题比较简单，层数的最小值实际上就是为完全二叉树的情况，层数的最大值实际上就是连成一根线的情况，结点数就是层数，所以说根据性质四得到最小深度为11，最大深度就直接1025了，k的范围是11 - 1025
将一棵树转换为二叉树时，根节点的右边连接的是？

根据我们前面总结得到的性质，树转换为二叉树之后，根节点一定没有右子树，所以为空

二叉树的构建

前面我们介绍了二叉树的几个重要性质，那么现在我们就来尝试在程序中表示和使用一棵二叉树。

二叉树的存储形式也可以使用我们前面的两种方式，一种是使用数组进行存放，还有一种就是使用链式结构，只不过之前链式结构需要强化一下才可以表示为二叉树。

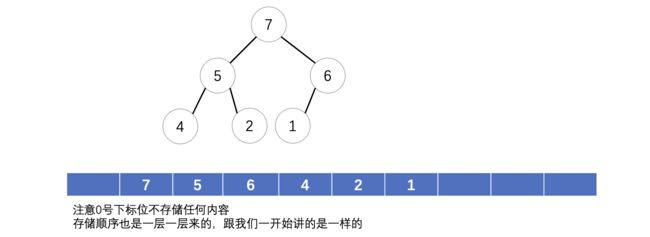
首先我们来看数组形式的表示方式，利用前面所推导的性质五，我们可以按照以下顺序进行存放：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NyPVbZJo-1683974297361)(https://s2.loli.net/2022/08/05/uan6A3ZRLykt289.png)]

这颗二叉树的顺序存储：

从左往右，编号i从1开始，比如现在我们需要获取A的右孩子，那么就需要根据性质五进行计算，因为右孩子为2i + 1，所以A的右边孩子的编号就是3，也就是结点C。

这种表示形式使用起来并不方便，而且存在大量的计算，所以说我们只做了解即可，我们的重点是下面的链式存储方式。

我们在前面使用链表的时候，每个结点不仅存放对应的数据，而且会存放一个指向下一个结点的指针：

而二叉树也可以使用这样的链式存储形式，只不过现在一个结点需要存放一个指向左子树的指针和一个指向右子树的指针了：

通过这种方式，我们就可以通过连接不同的结点形成一颗二叉树了，这样也更便于我们去理解它，我们首先定义一个结构体：

typedef char E;

struct TreeNode {
    E element;    //存放元素
    struct TreeNode * left;   //指向左子树的指针
    struct TreeNode * right;   //指向右子树的指针
};

typedef struct TreeNode * Node;

比如我们现在想要构建一颗像这样的二叉树：

首先我们需要创建好这几个结点：

int main(){
    Node a = malloc(sizeof(struct TreeNode));   //依次创建好这五个结点
    Node b = malloc(sizeof(struct TreeNode));
    Node c = malloc(sizeof(struct TreeNode));
    Node d = malloc(sizeof(struct TreeNode));
    Node e = malloc(sizeof(struct TreeNode));
  	a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
}

接着我们从最上面开始，挨着进行连接，首先是A这个结点：

int main(){
    ...

    a->left = b;   //A的左孩子是B
    a->right = c;   //A的右孩子是C
}

然后是B这个结点：

int main(){
    ...
      
    b->left = d;   //B的左孩子是D
    b->right = e;   //B的右孩子是E
  
  	//别忘了把其他的结点改为NULL
  	...
}

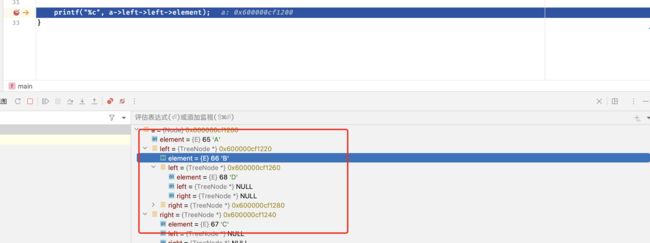
这样的话，我们就成功构建好了这棵二叉树：

int main(){
    ...

    printf("%c", a->left->left->element);   //比如现在我想要获取A左孩子的左孩子，那么就可以直接left二连
}

断点调试也可以看的很清楚：

二叉树的遍历

前面我们通过使用链式结构，成功构建出了一棵二叉树，接着我们来看看如何遍历一棵二叉树，也就是说我们想要访问二叉树的每一个结点，由于树形结构特殊，遍历顺序并不唯一，所以一共有四种访问方式：**前序遍历、中序遍历、后序遍历、层序遍历。**不同的访问方式输出都结点顺序也不同。

首先我们来看最简单的前序遍历：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-q1ifuidk-1683974297366)(https://s2.loli.net/2022/08/06/G6ujstSVZ2XWJLE.png)]

前序遍历是一种勇往直前的态度，走到哪就遍历到那里，先走左边再走右边，比如上面的这个图，首先会从根节点开始：

从A开始，先左后右，那么下一个就是B，然后继续走左边，是D，现在ABD走完之后，B的左边结束了，那么就要开始B的右边了，所以下一个是E，E结束之后，现在A的左子树已经全部遍历完成了，然后就是右边，接着就是C，C没有左子树了，那么只能走右边了，最后输出F，所以上面这个二叉树的前序遍历结果为：ABDECF

打印根节点
前序遍历左子树
前序遍历右子树

我们不难发现规律，整棵二叉树（包括子树）的根节点一定是出现在最前面的，比如A在最前面，A的左子树根结点B也是在最前面的。

接着我们来通过代码实现一下，首先先把咱们这棵二叉树组装好：

int main(){
    Node a = malloc(sizeof(struct TreeNode));
    Node b = malloc(sizeof(struct TreeNode));
    Node c = malloc(sizeof(struct TreeNode));
    Node d = malloc(sizeof(struct TreeNode));
    Node e = malloc(sizeof(struct TreeNode));
    Node f = malloc(sizeof(struct TreeNode));
    a->element = 'A';
    b->element = 'B';
    c->element = 'C';
    d->element = 'D';
    e->element = 'E';
    f->element = 'F';

    a->left = b;
    a->right = c;
    b->left = d;
    b->right = e;
    c->right = f;
    c->left = NULL;
    d->left = e->right = NULL;
    e->left = e->right = NULL;
    f->left = f->right = NULL;
}

组装好之后，我们来实现一下前序遍历的函数：

void preOrder(Node root){   //传入的是二叉树的根结点
    
}

那么现在我们拿到根结点之后该怎么去写呢？既然是走到哪里打印到哪里，那么我们就先打印一下当前结点的值：

void preOrder(Node root){
    printf("%c", root->element);   //不多bb先打印再说
}

打印完成之后，我们就按照先左后右的规则往后遍历下一个结点，这里我们就直接使用递归来完成：

void preOrder(Node root){
    printf("%c", root->element);
    preOrder(root->left);   //将左孩子结点递归交给下一级
    preOrder(root->right);  //等上面的一系列向左递归结束后，再以同样的方式去到右边
}

不过还没，我们的递归肯定是需要一个终止条件的，不可能无限地进行下去，如果已经走到底了，那么就不能再往下走了，所以：

void preOrder(Node root){
    if(root == NULL) return;   //如果走到NULL了，那就表示已经到头了，直接返回
    printf("%c", root->element);
    preOrder(root->left);
    preOrder(root->right);
}

最后我们来测试一下吧：

int main(){
 		...

    preOrder(a);
}

可以看到结果为：

这样我们就通过一个简单的递归操作完成了对一棵二叉树的前序遍历，如果不太好理解，建议结合调试进行观察。

当然也有非递归的写法，我们使用循环，但是就比较麻烦了，我们需要使用栈来帮助我们完成（实际上递归写法本质上也是在利用栈），我们依然是从第一个结点开始，先走左边，每向下走一步，先输出节点的值，然后将对应的结点丢到栈中，当走到尽头时，表示左子树已经遍历完成，接着就是从栈中依次取出栈顶节点，如果栈顶结点有右子树，那么再按照同样的方式遍历其右子树，重复执行上述操作，直到栈清空为止。

一路向左，不断入栈，直到尽头
到达尽头后，出栈，看看有没有右子树，如果没有就继续出栈，直到遇到有右子树的为止
拿到右子树后，从右子树开始，重复上述步骤，直到栈清空

比如我们还是以上面的这棵树为例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JcikZvOB-1683974297367)(https://s2.loli.net/2022/08/06/G6ujstSVZ2XWJLE.png)]

首先我们依然从根结点A出发，不断遍历左子树，沿途打印结果并将节点丢进栈中：

当遍历到D结点时，没有左子树了，此时将栈顶结点D出栈，发现没有右节点，继续出栈，得到B结点，接着得到当前结点的右孩子E结点，然后重复上述步骤：

接着发现E也没有左子树了，同样的，又开始出栈，此时E没有右子树，接着看A，A有右子树，所以继续从C开始，重复上述步骤：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HV96vuYF-1683974297369)(https://s2.loli.net/2022/08/06/K73cGsRUP6WO5iu.png)]

由于C之后没有左子树，那么就出栈获取右子树，此时得到结点F，继续重复上述步骤：

最后F出栈，没有右子树了，栈空，结束。

按照这个思路，我们来编写一下程序吧：

typedef char E;

struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
};

typedef struct TreeNode * Node;

//------------- 栈 -------------------
typedef Node T;   //这里栈内元素类型定义为上面的Node，也就是二叉树结点指针

struct StackNode {
    T element;
    struct StackNode * next;
};

typedef struct StackNode * SNode;  //这里就命名为SNode，不然跟上面冲突了就不好了

void initStack(SNode head){
    head->next = NULL;
}

_Bool pushStack(SNode head, T element){
    SNode node = malloc(sizeof(struct StackNode));
    if(node == NULL) return 0;
    node->next = head->next;
    node->element = element;
    head->next = node;
    return 1;
}

_Bool isEmpty(SNode head){
    return head->next == NULL;
}

T popStack(SNode head){
    SNode top = head->next;
    head->next = head->next->next;
    T e = top->element;
    free(top);
    return e;
}

//-------------------------------------

void preOrder(Node root){
    struct StackNode stack;  //栈先搞出来
    initStack(&stack);
    while (root || !isEmpty(&stack)){   //两个条件，只有当栈空并且节点为NULL时才终止循环
        while (root) {    //按照我们的思路，先不断遍历左子树，直到没有为止
            pushStack(&stack, root);   //途中每经过一个结点，就将结点丢进栈中
            printf("%c", root->element);   //然后打印当前结点元素值
            root = root->left;  //继续遍历下一个左孩子结点
        }
        root = popStack(&stack);  //经过前面的循环，明确左子树全部走完了，接着就是右子树了
        root = root->right;  //得到右孩子，如果有右孩子，下一轮会重复上面的步骤；如果没有右孩子那么这里的root就被赋值为NULL了，下一轮开始会直接跳过上面的while，继续出栈下一个结点再找右子树
    }
}

这样，我们就通过非递归的方式实现了前序遍历，可以看到代码是相当复杂的，也不推荐这样编写。

那么前序遍历我们了解完了，接着就是中序遍历了，中序遍历在顺序上与前序遍历不同，前序遍历是走到哪就打印到哪，而中序遍历需要先完成整个左子树的遍历后再打印，然后再遍历其右子树。

我们还是以上面的二叉树为例：

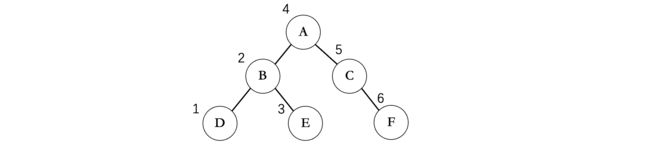
首先需要先不断遍历左子树，走到最底部，但是沿途并不进行打印，而是到底之后，再打印，所以第一个打印的是D，接着由于没有右子树，所以我们回到B，此时再打印B，然后再去看B的右结点E，由于没有左子树和右子树了，所以直接打印E，左边遍历完成，接着回到A，打印A，然后对A的右子树重复上述操作。所以说遍历的基本规则还是一样的，只是打印值的时机发生了改变。

中序遍历左子树
打印结点
中序遍历右子树

所以这棵二叉树的中序遍历结果为：DBEACF，我们可以发现一个规律，就是在某个结点的左子树中所有结点，其中序遍历结果也是按照这样的规律排列的，比如A的左子树中所有结点，中序遍历结果中全部都在A的左边，右子树中所有的结点，全部都在A的右边（这个规律很关键，后面在做一些算法题时会用到）

那么怎么才能将打印调整到左子树全部遍历结束之后呢？其实很简单：

void inOrder(Node root){
    if(root == NULL) return;
    inOrder(root->left);  //先完成全部左子树的遍历
    printf("%c", root->element);   //等待左子树遍历完成之后再打印
    inOrder(root->right);   //然后就是对右子树进行遍历
}

我们只需要将打印放到左子树遍历之后即可，这样打印出来的结果就是中序遍历的结果了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pzxg8c9Y-1683974297371)(https://s2.loli.net/2022/08/06/V2KdMy3T5Beo8vx.png)]

同样的，如果采用的是非递归，那么我也只需要稍微改动一个地方即可：

...
  
void inOrder(Node root){
    struct StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)){   //其他都不变
        while (root) {
            pushStack(&stack, root);
            root = root->left;
        }
        root = popStack(&stack);
        printf("%c", root->element);   //只需要将打印时机延后到左子树遍历完成
        root = root->right;
    }
}

这样，我们就实现了二叉树的中序遍历，实际上还是很好理解的。

接着我们来看一下后序遍历，后序遍历继续将打印的时机延后，需要等待左右子树全部遍历完成，才会去进行打印。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kvce814w-1683974297372)(https://s2.loli.net/2022/08/06/YE2rODdqpCInUa9.png)]

首先还是一路向左，到达结点D，此时结点D没有左子树了，接着看结点D还有没有右子树，发现也没有，左右子树全部遍历完成，那么此时再打印D，同样的，D完事之后就回到B了，此时接着看B的右子树，发现有结点E，重复上述操作，E也打印出来了，接着B的左右子树全部OK，那么再打印B，接着A的左子树就完事了，现在回到A，看到A的右子树，继续重复上述步骤，当A的右子树也遍历结束后，最后再打印A结点。

后序遍历左子树
后序遍历右子树
打印结点

所以最后的遍历顺序为：DEBFCA，不难发现，整棵二叉树（包括子树）根结点一定是在后面的，比如A在所有的结点的后面，B在其子节点D、E的后面，这一点恰恰和前序遍历相反（注意不是得到的结果相反，是规律相反）

所以，按照这个思路，我们来编写一下后序遍历：

void postOrder(Node root){
    if(root == NULL) return;
    postOrder(root->left);
    postOrder(root->right);
    printf("%c", root->element);   //时机延迟到最后
}

结果如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-x5WeQCST-1683974297372)(https://s2.loli.net/2022/08/06/6Vx9fmSUcqw51Mp.png)]

不过难点来了，后序遍历使用非递归貌似写不了啊？因为按照我们的之前的思路，最多也就实现中序遍历，我们没办法在一次循环中得知右子树是否完成遍历，难点就在这里。那么我们就要想办法先让右子树完成遍历，由于一个结点需要左子树全部完成+右子树全部完成，而目前只能明确左子树完成了遍历（也就是内层while之后，左子树一定结束了）所以我们可以不急着将结点出栈，而是等待其左右都完事了再出栈，这里我们需要稍微对结点的结构进行修改，添加一个标记变量，来表示已经完成左边还是左右都完成了：

struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int flag;   //需要经历左右子树都被遍历才行，这里用flag存一下状态，0表示左子树遍历完成，1表示右子树遍历完成
};

T peekStack(SNode head){   //这里新增一个peek操作，用于获取栈顶元素的值，但是不出栈，仅仅是值获取
    return head->next->element;
}

void postOrder(Node root){
    struct StackNode stack;
    initStack(&stack);
    while (root || !isEmpty(&stack)){   //其他都不变
        while (root) {
            pushStack(&stack, root);
            root->flag = 0;    //首次入栈时，只能代表左子树遍历完成，所以flag置0
            root = root->left;
        }
        root = peekStack(&stack);   //注意这里只是获取到结点，并没有进行出栈操作，因为需要等待右子树遍历完才能出栈
        if(root->flag == 0) {    //如果仅仅遍历了左子树，那么flag就等于0
            root->flag = 1;   //此时标记为1表示遍历右子树
            root = root->right;   //这里跟之前是一样的
        } else {
            printf("%c", root->element);   //当flag为1时走这边，此时左右都遍历完成了，这时再打印值出来
            popStack(&stack);   //这时再把对应的结点出栈，因为左右都完事了
            root = NULL;   //置为NULL，下一轮直接跳过while，然后继续取栈中剩余的结点，重复上述操作
        }
    }
}

所以，后序遍历的非递归写法的最大区别是将结点的出栈时机和打印时机都延后了。

最后我们来看层序遍历，实际上这种遍历方式是我们人脑最容易理解的，它是按照每一层在进行遍历：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-TpiLnUkZ-1683974297373)(https://s2.loli.net/2022/08/07/ywF6r9MU1JSPIge.png)]

层序遍历实际上就是按照从上往下每一层，从左到右的顺序打印每个结点，比如上面的这棵二叉树，那么层序遍历的结果就是：ABCDEF，像这样一层一层的挨个输出。

虽然理解起来比较简单，但是如果让你编程写出来，该咋搞？是不是感觉有点无从下手？

我们可以利用队列来实现层序遍历，首先将根结点存入队列中，接着循环执行以下步骤：

进行出队操作，得到一个结点，并打印结点的值。
将此结点的左右孩子结点依次入队。

不断重复以上步骤，直到队列为空。

我们来分析一下，首先肯定一开始A在里面：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-X9ILxtuH-1683974297373)(https://s2.loli.net/2022/08/07/ZsNpeVUivEjCymt.png)]

接着开始不断重复上面的步骤，首先是将队首元素出队，打印A，然后将A的左右孩子依次入队：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2aN5WK0M-1683974297374)(https://s2.loli.net/2022/08/07/v8yXWNato3sfeUn.png)]

现在队列中有B、C两个结点，继续重复上述操作，B先出队，打印B，然后将B的左右孩子依次入队：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HaY1lqwa-1683974297374)(https://s2.loli.net/2022/08/07/Qkprfi5RhAXP7Cd.png)]

现在队列中有C、D、E这三个结点，继续重复，C出队并打印，然后将F入队：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AQFC85bK-1683974297375)(https://s2.loli.net/2022/08/07/MxQTArlWK2gDjqi.png)]

我们发现，这个过程中，打印的顺序正好就是我们层序遍历的顺序，所以说队列还是非常有用的。

那么现在我们就来上代码吧：

typedef char E;

struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int flag;
};

typedef struct TreeNode * Node;

//--------------- 队列 ----------------
typedef Node T;   //还是将Node作为元素

struct QueueNode {
    T element;
    struct QueueNode * next;
};

typedef struct QueueNode * QNode;

struct Queue{
    QNode front, rear;
};

typedef struct Queue * LinkedQueue;

_Bool initQueue(LinkedQueue queue){
    QNode node = malloc(sizeof(struct QueueNode));
    if(node == NULL) return 0;
    queue->front = queue->rear = node;
    return 1;
}

_Bool offerQueue(LinkedQueue queue, T element){
    QNode node = malloc(sizeof(struct QueueNode));
    if(node == NULL) return 0;
    node->element = element;
    queue->rear->next = node;
    queue->rear = node;
    return 1;
}

_Bool isEmpty(LinkedQueue queue){
    return queue->front == queue->rear;
}

T pollQueue(LinkedQueue queue){
    T e = queue->front->next->element;
    QNode node = queue->front->next;
    queue->front->next = queue->front->next->next;
    if(queue->rear == node) queue->rear = queue->front;
    free(node);
    return e;
}
//--------------------------------

void levelOrder(Node root){
    struct Queue queue;   //先搞一个队列
    initQueue(&queue);
    offerQueue(&queue, root);  //先把根节点入队
    while (!isEmpty(&queue)) {   //不断重复，直到队列空为止
        Node node = pollQueue(&queue);   //出队一个元素，打印值
        printf("%c", node->element);
        if(node->left)    //如果存在左右孩子的话
            offerQueue(&queue, node->left);  //记得将左右孩子入队，注意顺序，先左后右
        if(node->right)
            offerQueue(&queue, node->right);
    }
}

可以看到结果就是层序遍历的结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2RAzMPAo-1683974297375)(https://s2.loli.net/2022/08/07/YlUfDhPoQrg9TkB.png)]

当然，使用递归也可以实现，但是需要单独存放结果然后单独输出，不是很方便，所以说这里就不演示了。

二叉树练习题：

现在有一棵二叉树前序遍历结果为：ABCDE，中序遍历结果为：BADCE，那么请问该二叉树的后序遍历结果为？
对二叉树的结点从1开始连续进行编号，要求每个结点的编号大于其左右孩子的编号，那么请问需要采用哪种遍历方式来实现？

A. 前序遍历 B. 中序遍历 C. 后序遍历 D. 层序遍历

高级树结构

高级树结构篇是对树结构的延伸扩展，有着特殊的定义和性质，在编写上可能会比较复杂，所以这一部分对于那些太过复杂的结构，就不进行代码编写了，只进行理论讲解。

线索化二叉树

前面我们学习了二叉树，我们知道一棵二叉树实际上可以由多个结点组成，每个结点都有一个左右指针，指向其左右孩子。我们在最后也讲解了二叉树的遍历，包括前序、中序、后序以及层序遍历。只不过在遍历时实在是太麻烦了，我们需要借助栈来帮助我们完成这项遍历操作。

实际上我们发现，一棵二叉树的某些结点会存在NULL的情况，我们可以利用这些为NULL的指针，将其线索化为某一种顺序遍历的指向下一个按顺序的结点的指针，这样我们在进行遍历的时候，就会很方便了。

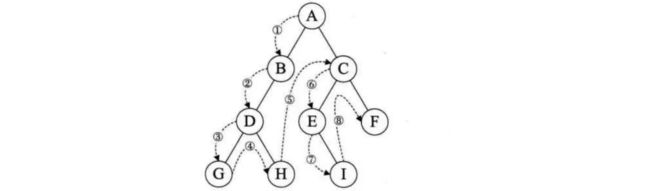
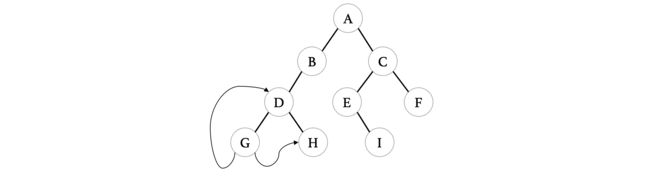
例如，一棵二叉树的前序遍历顺序如下：

我们就可以将其进行线索化，首先还是按照前序遍历的顺序依次寻找：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FHIDOOZe-1683974297376)(https://s2.loli.net/2022/08/14/Wu954jeLJhbxXDr.png)]

线索化的规则为：

结点的左指针，指向其当前遍历顺序的前驱结点。
结点的右指针，指向其当前遍历顺序的后继结点。

所以在线索化之后，G的指向情况如下：

这样，G原本两个为NULL的指针就被我们利用起来了，但是现在有一个问题，我们怎么知道，某个结点的指针到底是指向的其左右孩子，还是说某种遍历顺序下的前驱或是后继结点呢？所以，我们还需要分别为左右添加一个标志位，来表示左右指针到底指向的是孩子还是遍历线索：

typedef char E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int leftTag, rightTag;   //标志位，如果为1表示这一边指针指向的是线索，不为1就是正常的孩子结点
} * Node;

接着是H结点，同样的，因为H结点的左右指针都是NULL，那么我们也可以将其线索化：

接着我们来看结点E，这个结点只有一个右孩子，没有左孩子，左孩子指针为NULL，我们也可以将其线索化：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t0ptWe0L-1683974339347)(null)]

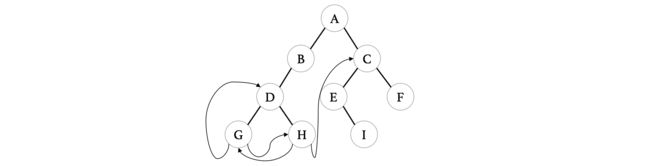
最后，整棵二叉树完成线索化之后，除了遍历顺序的最后一个结点没有后续之外，其他为NULL的指针都被利用起来了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gLpZ1ZZQ-1683974297378)(https://s2.loli.net/2022/08/14/SpWPAbzXRFcOgZJ.png)]

我们可以发现，在利用上那些为NULL的指针之后，当我们再次进行前序遍历时，我们不需要再借助栈了，而是可以一路向前。

这里我们弄一个简单一点的线索化二叉树，来尝试对其进行遍历：

首先我们要对这棵二叉树进行线索化，将其变成一棵线索化二叉树：

Node createNode(E element){   //单独写了个函数来创建结点
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->rightTag = node->leftTag = 0;
    node->element = element;
    return node;
}

int main() {
    Node a = createNode('A');
    Node b = createNode('B');
    Node c = createNode('C');
    Node d = createNode('D');
    Node e = createNode('E');

    a->left = b;
    b->left = d;
    a->right = c;
    b->right = e;
}

实际上要将其进行线索化，我们只需要正常按照对应的遍历顺序进行即可，不过在遍历过程中需要留意那些存在空指针的结点，我们需要修改其指针的指向：

void preOrderThreaded(Node root){   //前序遍历线索化函数
    if(root == NULL) return;
  	//别急着写打印
    preOrderThreaded(root->left);
    preOrderThreaded(root->right);
}

首先还是老规矩，先把前序遍历写出来，然后我们需要进行判断，如果存在指针指向为NULL，那么就将其线索化：

Node pre = NULL;  //这里我们需要一个pre来保存后续结点的指向
void preOrderThreaded(Node root){   //前序遍历线索化函数
    if(root == NULL) return;

    if(root->left == NULL) {   //首先判断当前结点左边是否为NULL，如果是，那么指向上一个结点
        root->left = pre;
        root->leftTag = 1;  //记得修改标记
    }
    if(pre && pre->right == NULL) {  //然后是判断上一个结点的右边是否为NULL，如果是那么进行线索化，指向当前结点
        pre->right = root;
        pre->rightTag = 1;  //记得修改标记
    }
    
    pre = root;   //每遍历完一个，需要更新一下pre，表示上一个遍历的结点

  	if(root->leftTag == 0)   //注意只有标志位是0才可以继续向下，否则就是线索了
    	preOrderThreaded(root->left);
  	if(root->rightTag == 0)
    	preOrderThreaded(root->right);
}

这样，在我们进行二叉树的遍历时，会自动将其线索化，线索化完成之后就是一棵线索化二叉树了。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FH4BMwgX-1683974297379)(https://s2.loli.net/2022/08/14/kxhAsiWCSYMdB7q.png)]

可以看到结点D的左右标记都是1，说明都被线索化了，并且D的左边指向的是其前一个结点B，右边指向的是后一个结点E，这样我们就成功将其线索化了。

现在我们成功得到了一棵线索化之后的二叉树，那么怎么对其进行遍历呢？我们只需要一个简单的循环就可以了：

void preOrder(Node root){  //前序遍历一棵线索化二叉树非常简单
    while (root) {   //到头为止
        printf("%c", root->element);   //因为是前序遍历，所以直接按顺序打印就行了
        if(root->leftTag == 0) 
            root = root->left;   //如果是左孩子，那么就走左边
        else
            root = root->right;   //如果左边指向的不是孩子，而是线索，那么就直接走右边，因为右边无论是线索还是孩子，都要往这边走了
    }
}

我们接着来看看中序遍历的线索化二叉树，整个线索化过程我们只需要稍微调整位置就行了：

Node pre = NULL;  //这里我们需要一个pre来保存后续结点的指向
void inOrderThreaded(Node root){   //前序遍历线索化函数
    if(root == NULL) return;
    if(root->leftTag == 0)
        inOrderThreaded(root->left);
  
    //------  线索化 -------  现在放到中间去，其他的还是一样的
    if(root->left == NULL) {
        root->left = pre;
        root->leftTag = 1;
    }
    if(pre && pre->right == NULL) {
        pre->right = root;
        pre->rightTag = 1;
    }
    pre = root;
    //--------------------
  
    if(root->rightTag == 0)
        inOrderThreaded(root->right);
}

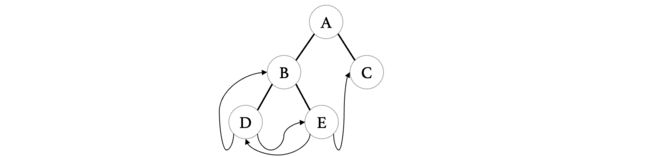
最后我们线索化完成之后，长这样了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-j62k0GQ0-1683974297380)(https://s2.loli.net/2022/08/14/tsEJLRFCYVaTOP8.png)]

那么像这样的一棵树，我们怎么对其进行遍历呢？中序遍历要稍微麻烦一些：

void inOrder(Node root){
    while (root) {   //因为中序遍历需要先完成左边，所以说要先走到最左边才行
        while (root && root->leftTag == 0)    //如果左边一直都不是线索，那么就一直往左找，直到找到一个左边是线索的为止，表示到头了
            root = root->left;

        printf("%c", root->element);   //到最左边了再打印，中序开始

        while (root && root->rightTag == 1) {   //打印完就该右边了，右边如果是线索化之后的结果，表示是下一个结点，那么就一路向前，直到不是为止
            root = root->right;
            printf("%c", root->element);   //注意按着线索往下就是中序的结果，所以说沿途需要打印
        }
        root = root->right;  //最后继续从右结点开始，重复上述操作
    }
}

最后我们来看看后序遍历的线索化，同样的，我们只需要在线索化时修改为后序就行了

Node pre = NULL;  //这里我们需要一个pre来保存后续结点的指向
void inOrderThreaded(Node root){   //前序遍历线索化函数
    if(root == NULL) return;
    if(root->leftTag == 0)
        inOrderThreaded(root->left);
    if(root->rightTag == 0)
        inOrderThreaded(root->right);
    //------  线索化 -------   现在这一坨移到最后，就是后序遍历的线索化了
    if(root->left == NULL) {
        root->left = pre;
        root->leftTag = 1;
    }
    if(pre && pre->right == NULL) {
        pre->right = root;
        pre->rightTag = 1;
    }
    pre = root;
    //--------------------
}

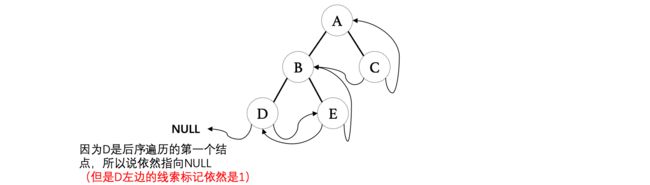
线索化完成之后，变成一棵后续线索化二叉树：

后序遍历的结果看起来有点怪怪的，但是这就是后序，那么怎么对这棵线索化二叉树进行后续遍历呢？这就比较复杂了。首先后续遍历需要先完成左右，左边还好说，关键是右边，右边完事之后我们并不一定能找到对应子树的根结点，比如我们按照上面的线索，先从D开始，根据线索找到E，然后继续跟据线索找到B，但是此时B无法找到其兄弟结点C，所以说这样是行不通的，因此要完成后续遍历，我们只能对结点进行改造：

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    struct TreeNode * parent;   //指向双亲（父）结点
    int leftTag, rightTag;
} * Node;

现在每个结点都保存其父结点，这样就可以顺利地找上去了。现在我们来编写一下吧：

Node pre = NULL;  //这里我们需要一个pre来保存后续结点的指向
void postOrderThreaded(Node root){   //前序遍历线索化函数
    if(root == NULL) return;
    if(root->leftTag == 0) {
        postOrderThreaded(root->left);
        if(root->left) root->left->parent = root;  //左边完事之后，如果不为空，那么就设定父子关系
    }
    if(root->rightTag == 0) {
        postOrderThreaded(root->right);
        if(root->right) root->right->parent = root;   //右边完事之后，如果不为空，那么就设定父子关系
    }
    //------  线索化 -------
    if(root->left == NULL) {
        root->left = pre;
        root->leftTag = 1;
    }
    if(pre && pre->right == NULL) {
        pre->right = root;
        pre->rightTag = 1;
    }
    pre = root;
    //--------------------
}

后序遍历代码如下：

void postOrder(Node root){
    Node last = NULL, node = root;  //这里需要两个暂存指针，一个记录上一次遍历的结点，还有一个从root开始
    while (node) {
        while (node->left != last && node->leftTag == 0)    //依然是从整棵树最左边结点开始，和前面一样，只不过这里加入了防无限循环机制，看到下面就知道了
            node = node->left;
        while (node && node->rightTag == 1) {   //左边完了还有右边，如果右边是线索，那么直接一路向前，也是跟前面一样的
            printf("%c", node->element);   //沿途打印
            last = node;
            node = node->right;
        }
        if (node == root && node->right == last) {
            //上面的操作完成之后，那么当前结点左右就结束了，此时就要去寻找其兄弟结点了，我们可以
            //直接通过parent拿到兄弟结点，但是如果当前结点是根结点，需要特殊处理，因为根结点没有父结点了
            printf("%c", node->element);
            return;   //根节点一定是最后一个，所以说直接返回就完事
        }
        while (node && node->right == last) {    //如果当前结点的右孩子就是上一个遍历的结点，那么一直向前就行
            printf("%c", node->element);   //直接打印当前结点
            last = node;
            node = node->parent;
        }
        //到这里只有一种情况了，是从左子树上来的，那么当前结点的右边要么是线索要么是右子树，所以直接向右就完事
        if(node && node->rightTag == 0) {  //如果不是线索，那就先走右边，如果是，等到下一轮再说
            node = node->right;
        }
    }
}

至此，有关线索化二叉树，我们就讲解到这样。

二叉查找树

还记得我们开篇讲到的二分搜索算法吗？通过不断缩小查找范围，最终我们可以以很高的效率找到有序数组中的目标位置。而二叉查找树则利用了类似的思想，我们可以借助其来像二分搜索那样快速查找。

二叉查找树也叫二叉搜索树或是二叉排序树，它具有一定的规则：

左子树中所有结点的值，均小于其根结点的值。
右子树中所有结点的值，均大于其根结点的值。
二叉搜索树的子树也是二叉搜索树。

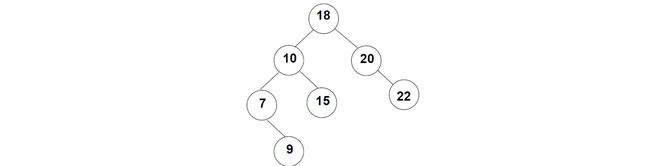
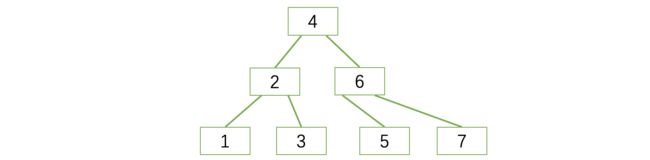
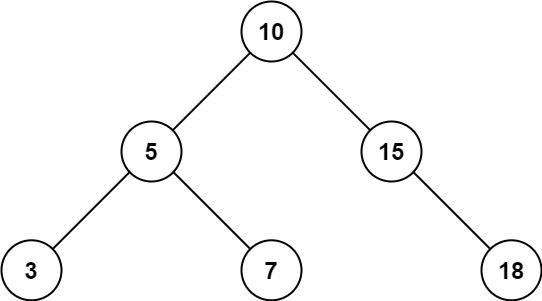
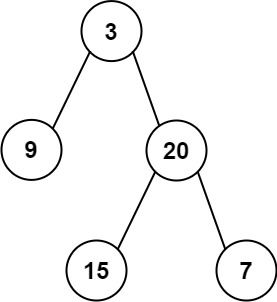
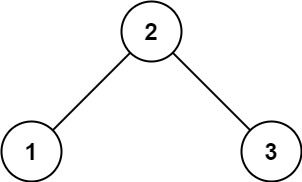
一棵二叉搜索树长这样：

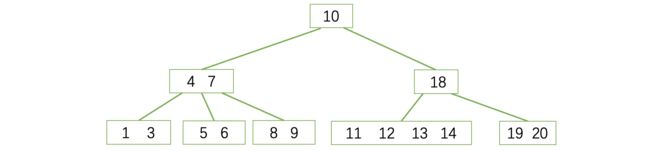
这棵树的根结点为18，而其根结点左边子树的根结点为10，包括后续结点，都是满足上述要求的。二叉查找树满足左边一定比当前结点小，右边一定比当前结点大的规则，比如我们现在需要在这颗树种查找值为15的结点：

从根结点18开始，因为15小于18，所以从左边开始找。
接着来到10，发现10比15小，所以继续往右边走。
来到15，成功找到。

实际上，我们在对普通二叉树进行搜索时，可能需要挨个进行查看比较，而有了二叉搜索树，查找效率就大大提升了，它就像我们前面的二分搜索那样。

因为二叉搜索树要求比较严格，所以我们在插入结点时需要遵循一些规律，这里我们来尝试编写一下：

#include 
#include 

typedef int E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
} * Node;

Node createNode(E element){
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    return node;
}

int main() {
    
}

我们就以上面这颗二叉查找树为例，现在我们想要依次插入这些结点，我们需要编写一个特殊的插入操作，这里需要注意一下，二叉查找树不能插入重复元素，如果出现重复直接忽略：

Node insert(Node root, E element){
    if(root){
        if(root->element > element)    //如果插入结点值小于当前结点，那么说明应该放到左边去
            root->left = insert(root->left, element);
        else if(root->element < element)    //如果插入结点值大于当前结点，那么说明应该放到右边去
            root->right = insert(root->right, element);
    } else {   //当结点为空时，说明已经找到插入的位置了，创建对应结点
        root = createNode(element);
    }
    return root;   //返回当前结点
}

这样我们就可以通过不断插入创建一棵二叉查找树了：

void inOrder(Node root){
    if(root == NULL) return;
    inOrder(root->left);
    printf("%d ", root->element);
    inOrder(root->right);
}

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    inOrder(root);   //用中序遍历查看一下结果
}

我们按照顺序来，首先是根结点的左右孩子，分别是10和20，那么这里我们就依次插入一下：

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    insert(root, 10);
    insert(root, 20);
    inOrder(root);
}

可以看到中序结果为：

比18小的结点在左边，大的在右边，满足二叉查找树的性质。接着是7、15、22：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eRqMKqkI-1683974297382)(https://s2.loli.net/2022/08/15/chEUaOBzCTl4N8G.png)]

最后再插入9就是我们上面的这棵二叉查找树了。当然我们直接写成控制台扫描的形式，就更方便了：

int main() {
    Node root = NULL;
    while (1) {
        E element;
        scanf("%d", &element);
        root = insert(root, element);
        inOrder(root);
        putchar('\n');
    }
}

那么插入写好之后，我们怎么找到对应的结点呢？实际上也是按照规律来就行了：

Node find(Node root, E target){
    while (root) {
        if(root->element > target)    //如果要找的值比当前结点小，说明肯定在左边
            root = root->left;
        else if(root->element < target)   //如果要找的值比当前结点大，说明肯定在右边
            root = root->right;
        else
            return root;   //等于的话，说明找到了，就直接返回
    }
    return NULL;   //都找到底了还没有，那就是真没有了
}

Node findMax(Node root){   //查找最大值就更简单了，最右边的一定是最大的
    while (root && root->right) 
        root = root->right;
    return root;
}

我们来尝试查找一下：

int main() {
    Node root = insert(NULL, 18);   //插入后，得到根结点
    insert(root, 10);
    insert(root, 20);
    insert(root, 7);
    insert(root, 15);
    insert(root, 22);
    insert(root, 9);

    printf("%p\n", find(root, 17));
    printf("%p\n", find(root, 9));
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9uKRkaue-1683974297382)(https://s2.loli.net/2022/08/15/lFOaUphkbB3wxIC.png)]

搜索17的结果为NULL，说明没有这个结点，而9则成功找到了。

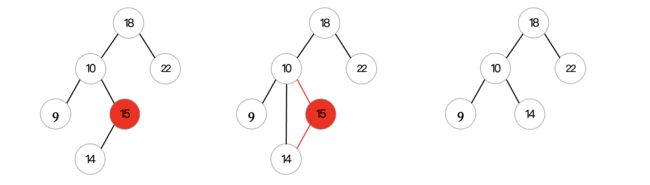
最后我们来看看二叉查找树的删除操作，这个操作就比较麻烦了，因为可能会出现下面的几种情况：

要删除的结点是叶子结点。
要删除的结点是只有一个孩子结点。
要删除的结点有两个孩子结点。

首先我们来看第一种情况，这种情况实际上最好办，直接删除就完事了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Z0wO9rZc-1683974297383)(https://s2.loli.net/2022/08/15/7RWkPXh6po2HjNz.png)]

而第二种情况，就有点麻烦了，因为有一个孩子，就像一个拖油瓶一样，你离开了还不行，你还得对他负责才可以。当移除后，需要将孩子结点连接上去：

可以看到在调整后，依然满足二叉查找树的性质。最后是最麻烦的有两个孩子的情况，这种该怎么办呢？前面只有一个孩子直接上位就完事，但是现在两个孩子，到底谁上位呢？这就不好办了，为了保持二叉查找树的性质，现在有两种选择：

选取其左子树中最大结点上位
选择其右子树中最小结点上位

这里我们以第一种方式为例：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6RT03DEw-1683974297385)(https://s2.loli.net/2022/08/15/jPRG68tru4bvIFa.png)]

现在我们已经分析完三种情况了，那么我们就来编写一下代码吧：

Node delete(Node root, E target){
    if(root == NULL) return NULL;   //都走到底了还是没有找到要删除的结点，说明没有，直接返回空
    if(root->element > target)   //这里的判断跟之前插入是一样的，继续往后找就完事，直到找到为止
        root->left = delete(root->left, target);
    else if(root->element < target)
        root->right = delete(root->right, target);
    else {   //这种情况就是找到了
        if(root->left && root->right) {   //先处理最麻烦的左右孩子都有的情况
            Node max = findMax(root->left);  //寻找左子树中最大的元素
            root->element = max->element;  //找到后将值替换
            root->left = delete(root->left, root->element);  //替换好后，以同样的方式去删除那个替换上来的结点
        } else {   //其他两种情况可以一起处理，只需要删除这个结点就行，然后将root指定为其中一个孩子，最后返回就完事
            Node tmp = root;
            if(root->right) {   //不是左边就是右边
                root = root->right;
            } else {
                root = root->left;
            }
            free(tmp);   //开删
        }
    }
    return root;   //返回最终的结点
}

这样，我们就完成了二叉查找树的各种操作，当然目前为止我们了解的二叉树高级结构还比较简单，后面就开始慢慢复杂起来了。

平衡二叉树

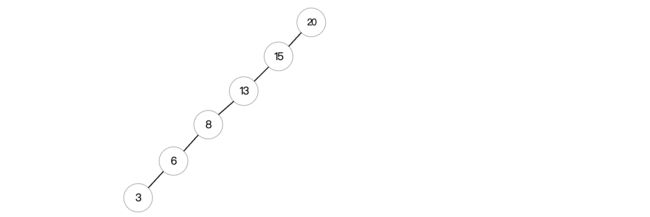
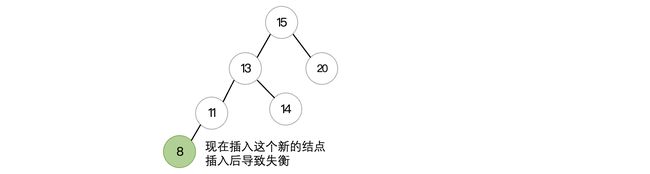
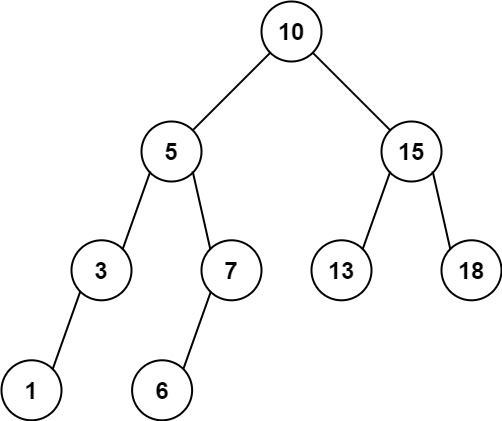
前面我们介绍了二叉查找树，利用二叉查找树，我们在搜索某个值的时候，效率会得到巨大提升。但是虽然看起来比较完美，也是存在缺陷的，比如现在我们依次将下面的值插入到这棵二叉树中：

20 15 13 8 6 3

在插入完成后，我们会发现这棵二叉树竟然长这样：

因为根据我们之前编写的插入规则，小的一律往左边放，现在正好来的就是这样一串递减的数字，最后就组成了这样的一棵只有一边的二叉树，这种情况，与其说它是一棵二叉树，不如说就是一个链表，如果这时我们想要查找某个结点，那么实际上查找的时间并没有得到任何优化，直接就退化成线性查找了。

所以，二叉查找树只有在理想情况下，查找效率才是最高的，而像这种极端情况，就性能而言几乎没有任何的提升。我们理想情况下，这样的效率是最高的：

所以，我们在进行结点插入时，需要尽可能地避免这种一边倒的情况，这里就需要引入平衡二叉树的概念了。实际上我们发现，在插入时如果不去维护二叉树的平衡，某一边只会无限制地延伸下去，出现极度不平衡的情况，而我们理想中的二叉查找树左右是尽可能保持平衡的，平衡二叉树（AVL树）就是为了解决这样的问题而生的。

它的性质如下：

平衡二叉树一定是一棵二叉查找树。
任意结点的左右子树也是一棵平衡二叉树。
从根节点开始，左右子树都高度差不能超过1，否则视为不平衡。

可以看到，这些性质规定了平衡二叉树需要保持高度平衡，这样我们的查找效率才不会因为数据的插入而出现降低的情况。二叉树上节点的左子树高度减去右子树高度，得到的结果称为该节点的平衡因子（Balance Factor），比如：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lGRUhG4N-1683974297386)(https://s2.loli.net/2022/08/15/vaI9qji1KYOP8kt.png)]

通过计算平衡因子，我们就可以快速得到是否出现失衡的情况。比如下面的这棵二叉树，正在执行插入操作：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-B2fzZ9Ba-1683974297387)(https://s2.loli.net/2022/08/15/DMnPqGhawy5Z92V.png)]

可以看到，当插入之后，不再满足平衡二叉树的定义时，就出现了失衡的情况，而对于这种失衡情况，为了继续保持平衡状态，我们就需要进行处理了。我们可能会遇到以下几种情况导致失衡：

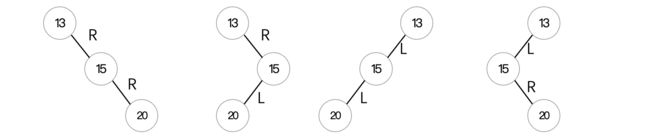
根据插入结点的不同偏向情况，分为LL型、LR型、RR型、RL型。针对于上面这几种情况，我们依次来看一下如何进行调整，使得这棵二叉树能够继续保持平衡：

动画网站：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html（实在不理解可以看看动画是怎么走的）

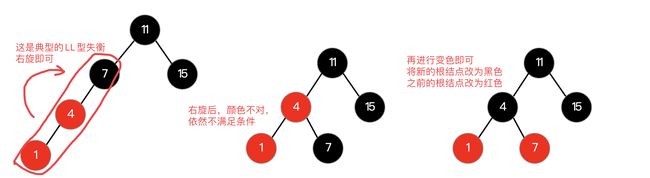
LL型调整（右旋）

首先我们来看这种情况，这是典型的LL型失衡，为了能够保证二叉树的平衡，我们需要将其进行旋转来维持平衡，去纠正最小不平衡子树即可。那么怎么进行旋转呢？对于LL型失衡，我们只需要进行右旋操作，首先我们先找到最小不平衡子树，注意是最小的那一个：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-z7Hn5Z2O-1683974297389)(https://s2.loli.net/2022/08/15/q4aYvzrnjdTgAtK.png)]

可以看到根结点的平衡因子是2，是目前最小的出现不平衡的点，所以说从根结点开始向左的三个结点需要进行右旋操作，右旋需要将这三个结点中间的结点作为新的根结点，而其他两个结点现在变成左右子树：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eaC885uJ-1683974297389)(https://s2.loli.net/2022/08/15/fJKz3FWclm9orVT.png)]

这样，我们就完成了右旋操作，可以看到右旋之后，所有的结点继续保持平衡，并且依然是一棵二叉查找树。
RR型调整（左旋）

前面我们介绍了LL型以及右旋解决方案，相反的，当遇到RR型时，我们只需要进行左旋操作即可：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-U6hvuwQs-1683974297390)(https://s2.loli.net/2022/08/15/kIl8ZT6Psr7mNSg.png)]

操作和上面是一样的，只不过现在反过来了而已：

这样，我们就完成了左旋操作，使得这棵二叉树继续保持平衡状态了。
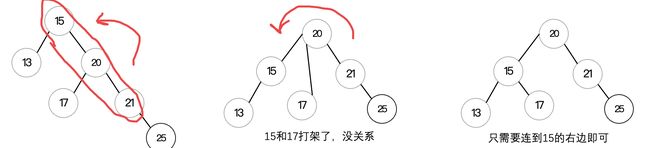
RL型调整（先右旋，再左旋）

剩下两种类型比较麻烦，需要旋转两次才行。我们来看看RL型长啥样：

可以看到现在的形状是一个回旋镖形状的，先右后左的一个状态，也就是RL型，针对于这种情况，我们需要先进行右旋操作，注意这里的右旋操作针对的是后两个结点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LHDwe5TS-1683974297391)(https://s2.loli.net/2022/08/15/ukK6C4PNBwoaJbc.png)]

其中右旋和左旋的操作，与之前一样，该怎么分配左右子树就怎么分配，完成两次旋转后，可以看到二叉树重新变回了平衡状态。
LR型调整（先左旋，再右旋）

和上面一样，我们来看看LR型长啥样，其实就是反着的：

形状是先向左再向右，这就是典型的LR型了，我们同样需要对其进行两次旋转：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vYQSWiyW-1683974297392)(https://s2.loli.net/2022/08/15/y6WscFPxHuzTiaI.png)]

这里我们先进行的是左旋，然后再进行的右旋，这样二叉树就能继续保持平衡了。

这样，我们只需要在插入结点时注意维护整棵树的平衡因子，保证其处于稳定状态，这样就可以让这棵树一直处于高度平衡的状态，不会再退化了。这里我们就编写一个插入结点代码来实现一下吧，首先还是结点定义：

typedef int E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int height;   //每个结点需要记录当前子树的高度，便于计算平衡因子
} * Node;

Node createNode(E element){
    Node node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->element = element;
    node->height = 1;   //初始化时，高度写为1就可以了
    return node;
}

接着我们需要先将左旋、右旋等操作编写出来，因为一会插入时可能需要用到：

int max(int a, int b){
    return a > b ? a : b;
}

int getHeight(Node root){
    if(root == NULL) return 0;
    return root->height;
}

Node leftRotation(Node root){  //左旋操作，实际上就是把左边结点拿上来
    Node newRoot = root->right;   //先得到左边结点
    root->right = newRoot->left;   //将左边结点的左子树丢到原本根结点的右边去
    newRoot->left = root;   //现在新的根结点左边就是原本的跟结点了

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}

Node rightRotation(Node root){
    Node newRoot = root->left;
    root->left = newRoot->right;
    newRoot->right = root;

    root->height = max(getHeight(root->right), getHeight(root->left)) + 1;
    newRoot->height = max(getHeight(newRoot->right), getHeight(newRoot->left)) + 1;
    return newRoot;
}

Node leftRightRotation(Node root){
    root->left = leftRotation(root->left);
    return rightRotation(root);
}

Node rightLeftRightRotation(Node root){
    root->right = rightRotation(root->right);
    return leftRotation(root);
}

最后就是我们的插入操作了，注意在插入时动态计算树的高度，一旦发现不平衡，那么就立即采取对应措施：

Node insert(Node root, E element){
    if(root == NULL) {    //如果结点为NULL，说明找到了插入位置，直接创建新的就完事
        root = createNode(element);
    }else if(root->element > element) {   //和二叉搜索树一样，判断大小，该走哪边走哪边，直到找到对应插入位置
        root->left = insert(root->left, element);
        if(getHeight(root->left) - getHeight(root->right) > 1) {   //插入完成之后，需要计算平衡因子，看看是否失衡
            if(root->left->element > element) //接着需要判断一下是插入了左子树的左边还是右边，如果是左边那边说明是LL，如果是右边那说明是LR
                root = rightRotation(root);   //LL型得到左旋之后的结果，得到新的根结点
            else
                root = leftRightRotation(root);    //LR型得到先左旋再右旋之后的结果，得到新的根结点
        }
    }else if(root->element < element){
        root->right = insert(root->right, element);
        if(getHeight(root->left) - getHeight(root->right) < -1){
            if(root->right->element < element)
                root = leftRotation(root);
            else
                root = rightLeftRightRotation(root);
        }
    }
    //前面的操作完成之后记得更新一下树高度
    root->height = max(getHeight(root->left), getHeight(root->right)) + 1;
    return root;  //最后返回root到上一级
}

这样，我们就完成了平衡二叉树的插入操作，当然删除操作比较类似，也是需要在删除之后判断是否平衡，如果不平衡同样需要进行旋转操作，这里就不做演示了。

红黑树

**注意：**本小节内容作为选学内容，不强制要求掌握。很多人都说红黑树难，其实就那几条规则，跟着我推一遍其实还是很简单的，当然前提是一定要把前面的平衡二叉树搞明白。

前面我们讲解了二叉平衡树，通过在插入结点时维护树的平衡，这样就不会出现极端情况使得整棵树的查找效率急剧降低了。但是这样是否开销太大了一点，因为一旦平衡因子的绝对值超过1那么就失衡，这样每插入一个结点，就有很大的概率会导致失衡，我们能否不这么严格，但同时也要在一定程度上保证平衡呢？这就要提到红黑树了。

在线动画网站：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

红黑树也是二叉查找树的一种，它大概长这样，可以看到结点有红有黑：

它并不像平衡二叉树那样严格要求高度差不能超过1，而是只需要满足五个规则即可，它的规则如下：

规则1：每个结点可以是黑色或是红色。
规则2：根结点一定是黑色。
规则3：红色结点的父结点和子结点不能为红色，也就是说不能有两个连续的红色。
规则4：所有的空结点都是黑色（空结点视为NIL，红黑树中是将空节点视为叶子结点）
规则5：每个结点到空节点（NIL）路径上出现的黑色结点的个数都相等。

它相比平衡二叉树，通过不严格平衡和改变颜色，就能在一定程度上减少旋转次数，这样的话对于整体性能是有一定提升的，只不过我们在插入结点时，就有点麻烦了，我们需要同时考虑变色和旋转这两个操作了，但是会比平衡二叉树更简单。

那么什么时候需要变色，什么时候需要旋转呢？我们通过一个简单例子来看看：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-atZBWo7P-1683974297393)(https://s2.loli.net/2022/08/16/wIj5qnhxFAHcyG7.png)]

首先这棵红黑树只有一个根结点，因为根结点必须是黑色，所以说直接变成黑色。现在我们要插入一个新的结点了，所有新插入的结点，默认情况下都是红色：

所以新来的结点7根据规则就直接放到11的左边就行了，然后注意7的左右两边都是NULL，那么默认都是黑色，这里就不画出来了。同样的，我们往右边也来一个：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iKYeFf1c-1683974297394)(https://s2.loli.net/2022/08/16/kJiA71fQuKHnIdb.png)]

现在我们继续插入一个结点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2iy2CmY1-1683974297394)(https://s2.loli.net/2022/08/16/VEQLu5mb1tcTyzd.png)]

插入结点4之后，此时违反了红黑树的规则3，因为红色结点的父结点和子结点不能为红色，此时为了保持以红黑树的性质，我们就需要进行颜色变换才可以，那么怎么进行颜色变换呢？我们只需要直接将父结点和其兄弟结点同时修改为黑色（为啥兄弟结点也需要变成黑色？因为要满足性质5）然后将爷爷结点改成红色即可：

当然这里还需注意一下，因为爷爷结点正常情况会变成红色，相当于新来了个红色的，这时还得继续往上看有没有破坏红黑树的规则才可以，直到没有为止，比如这里就破坏了性质一，爷爷结点现在是根结点（不是根结点就不需要管了），必须是黑色，所以说还要给它改成黑色才算结束：

接着我们继续插入结点：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3FPfSe5m-1683974297395)(https://s2.loli.net/2022/08/16/4ZAhv7R9YusI8q6.png)]

此时又来了一个插在4左边的结点，同样是连续红色，我们需要进行变色才可以讲解问题，但是我们发现，如果变色的话，那么从11开始到所有NIL结点经历的黑色结点数量就不对了：

所以说对于这种父结点为红色，父结点的兄弟结点为黑色（NIL视为黑色）的情况，变色无法解决问题了，那么我们只能考虑旋转了，旋转规则和我们之前讲解的平衡二叉树是一样的，这实际上是一种LL型失衡：

同样的，如果遇到了LR型失衡，跟前面一样，先左旋在右旋，然后进行变色即可：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UgBjzbB0-1683974297397)(https://s2.loli.net/2022/08/16/XqFr7hJwe38AakK.png)]

而RR型和RL型同理，这里就不进行演示了，可以看到，红黑树实际上也是通过颜色规则在进行旋转调整的，当然旋转和变色的操作顺序可以交换。所以，在插入时比较关键的判断点如下：

如果整棵树为NULL，直接作为根结点，变成黑色。
如果父结点是黑色，直接插入就完事。
如果父结点为红色，且父结点的兄弟结点也是红色，直接变色即可（但是注意得继续往上看有没有破坏之前的结构）
如果父结点为红色，但父结点的兄弟结点为黑色，需要先根据情况（LL、RR、LR、RL）进行旋转，然后再变色。

在了解这些步骤之后，我们其实已经可以尝试去编写一棵红黑树出来了，当然代码太过复杂，这里就不演示了。其实红黑树难点并不在于如何构建和使用，而是在于，到底是怎么设计出来的，究竟要多么丰富的知识储备才能想到如此精妙的规则。

红黑树的发明者：

红黑树（Red Black Tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

红黑树是在1972年由[Rudolf Bayer](https://baike.baidu.com/item/Rudolf Bayer/3014716)发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。

在了解了后面的B树之后，相信我们就能揭开这层神秘面纱了。

其他树结构

前面我们介绍了各种各样的二叉树，其实还是比较简单的。我们接着来看一下其他的一些树结构，这一部分我们只做了解即可。

B树和B+树

前面我们介绍了多种多样的二叉树，有线索化二叉树，平衡二叉树等等，这些改造版二叉树无疑都是为了提高我们的程序运行效率而生的，我们接着来看一种同样为了提升效率的树结构。

这里首先介绍一下B树（Balance Tree），它是专门为磁盘数据读取设计的一种度为 m 的查找树（多用于数据库）它同样是一棵平衡树，但是不仅限于二叉了，之前我们介绍的这些的二叉树都是基于内存读取的优化，磁盘读取速度更慢，它同样需要优化，一棵度为4的（4阶）B树大概长这样：

第一眼看上去，感觉好像没啥头绪，不能发现啥规律，但是只要你仔细观察，你会发现，它和二叉查找树很相似，左边的一定比根节点小，右边的一定比根节点大，并且我们发现，每个结点现在可以保存多个值，每个结点可以连接多个子树，这些值两两组合划分了一些区间，比如60左边，一定是比60小的，60和80之间那么就是大于60小于80的值，以此类推，所以值有N个，就可以划分出N+1个区间，那么子树最多就可以有N+1个。它的详细规则如下：

树中每个结点最多含有m个孩子（m >= 2）比如上面就是m为4的4阶B树，最多有4个孩子。
除根结点和叶子结点外，其它每个结点至少有⌈m/2⌉个孩子，同理键值数量至少有⌈m/2⌉-1个。
若根结点不是叶子结点，则至少有2个孩子。
所有叶子结点都出现在同一层。
一个结点的包含多种信息（P0，K1，P1，K2，…，Kn，Pn），其中P为指向子树的指针，K为键值（关键字）
1. Ki (i=1…n)为键值，也就是每个结点保存的值，且键值按顺序升序排序K(i-1)< Ki
2. Pi为指向子树的指针，且指针Pi指向的子树中所有结点的键值均小于Ki，但都大于K(i-1)
3. 键值的个数n必须满足： ⌈m/2⌉-1 <= n <= m-1

在线动画网站：https://www.cs.usfca.edu/~galles/visualization/BTree.html

是不是感觉怎么要求这么多呢？我们通过感受一下B树的插入和删除就知道了，首先是B树的插入操作，这里我们以度为3的B树为例：

插入1之后，只有一个结点，我们接着插入一个2，插入元素满足以下规则：

如果该节点上的元素数未满，则将新元素插入到该节点，并保持节点中元素的顺序。

所以，直接放进去就行，注意顺序：

接着我们再插入一个3进去，但是此时因为度为3，那么键值最多只能有两个，肯定是装不下了：

如果该节点上的元素已满，则需要将该节点平均地分裂成两个节点：
1. 首先从该节点中的所有元素和新元素中先出一个中位数作为分割值。
2. 小于中位数的元素作为左子树划分出去，大于中位数的元素作为右子树划分。
3. 分割值此时上升到父结点中，如果没有父结点，那么就创建一个新的（这里的上升不太好理解，一会我们推过去就明白了）

所以，当3来了之后，直接进行分裂操作：

就像爱情一样，两个人的世界容不下第三者，如果来了第三者，那么最后的结果大概率就是各自分道扬镳。接着我们继续插入4、5看看会发生什么，注意插入还是按照小的走左边，大的走右边的原则，跟我们之前的二叉查找树是一样的：

此时4、5来到了右边，现在右边这个结点又被撑爆了，所以说需要按照上面的规则，继续进行分割：

可能各位看着有点奇怪，为啥变成这样了，首先3、4、5三个都分开了，然后4作为分割值，3、5变成两个独立的树，此时4需要上升到父结点，所以直接跑到上面去了，然后3和5出现在4的左右两边。注意这里不是向下划分，反而有点向上划分的意思。为什么不向下划分呢？因为要满足B树第四条规则：所有叶子结点都出现在同一层。

此时我们继续插入6、7，看看会发生什么情况：

此时右下角结点又被挤爆了，右下角真是多灾多难啊，那么依然按照我们之前的操作进行分裂：

我们发现当新的分割值上升之后最上面的结点又被挤爆了，此时我们需要继续分裂：

在2、4、6中寻找一个新的分割值，分裂后将其上升到新的父结点中，就像上图那样了。在了解了B树的插入操作之后，是不是有一点感受到这种结构带来的便捷了？

我们再来看看B树的删除操作，这个要稍微麻烦一些，这里我们以一颗5阶B树为例，现在我们想删除16结点：

删除后，依然满足B树的性质，所以说什么都不管用：

此时我们接着去删除15结点：

删除后，现在结点中只有14了，不满足B树的性质：除根结点和叶子结点外，其它每个结点至少有⌈m/2⌉个孩子，同理键值数量至少有⌈m/2⌉-1个，现在只有一个肯定是不行的。此时我们需向兄弟（注意只能找左右两边的兄弟）借一个过来：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-i5mtrHXN-1683974339046)(null)]

此时我们继续删掉17，但是兄弟已经没办法再借给我们一个元素了，此时只能采取方案二，合并兄弟节点与分割键。这里我们就合并左边的这个兄弟吧：

现在他们三个又合并回去了，这下总满足了吧？但是我们发现，父结点此时只有一个元素了，又出问题了。同样的，还是先去找兄弟结点借一个，但是兄弟结点也借不了了，此时继续采取我们的方案二，合并：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dNgPDpzs-1683974297406)(https://s2.loli.net/2022/08/17/E2RzTW5XOJjHdQm.png)]

OK，这样才算是满足了B树的性质，现在我们继续删除4结点：

这种情况会导致失去分割值，那么我们得找一个新的分割值才行，这里取左边最大的：

不过此时虽然解决了分割值的问题，但是新的问题来了，左边结点不满足性质了，元素数量低于限制，于是需要找兄弟结点借，但是没得借了，兄弟也没有多的可以借了所以被迫合并了：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DTvQLWG8-1683974297408)(https://s2.loli.net/2022/08/17/jhT5SNFXwq9niYk.png)]

可以看到整个变换过程中，这颗B树所有子树的高度是一直维持在一个稳定状态的，查找效率能够持续保持。

删除操作可以总结为两大类：

若删除的是叶子结点的中元素：
- 正常情况下直接删除。
- 如果删除后，键值数小于最小值，那么需要找兄弟借一个。
- 要是没得借了，直接跟兄弟结点、对应的分割值合并。
若删除的是某个根结点中的元素：
- 一般情况会删掉一个分割值，删掉后需要重新从左右子树中找一个新分割值的拿上来。
- 要是拿上来之后左右子树中出现键值数小于最小值的情况，那么就只能合并了。
上述两个操作执行完后，还要继续往上看上面的结点是否依然满足性质，否则继续处理，直到稳定。

在了解了B树的相关操作之后，是不是感觉还是挺简单的，依然是动态维护树的平衡。正是得益于B树这种结点少，高度平衡且有序的性质，而硬盘IO速度远低于内存，我们希望能够花费尽可能少的时间找到我们想要的数据，减少IO次数，B树就非常适合在硬盘上的保存数据，它的查找效率是非常高的。

注意：以下内容为选学部分：

此时此刻，我们回想一下之前提到的红黑树，我们来看看它和B树有什么渊源，这是一棵很普通的红黑树：

此时我们将所有红色节点上移到与父结点同一高度，

还是没看出来？没关系，我们来挨个画个框：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-c9CXBATi-1683974334861)(null)]

woc，这不就是B树吗？没错，红黑树 和 4阶B树（2-3-4树）具有等价性，其中黑色结点就是中间的（黑色结点一定是父结点)，红色结点分别位于两边，通过将黑色结点与它的红色子节点融合在一起，形成1个B树节点，最后就像这样：

你会发现，红黑树的黑色节点个数总是与4阶B树的节点数相等。我们可以对比一下之前的红黑树插入和4阶B树的插入，比如现在我们想要插入一个新的14结点进来：

经过变色，最后得到如下的红黑树，此时又出现两个红色结点连续，因为父结点的兄弟结点依然是红色，继续变色：

最后因为根结点必须是黑色，所以说将60变为黑色，这样就插入成功了：

我们再来看看与其等价的B树插入14后会怎么样：

由于B树的左边被挤爆了，所以说需要分裂，因为是偶数个，需要选择中间偏右的那个数作为分割值，也就是25：

分裂后，分割值上升，又把父结点给挤爆了，所以说需要继续分裂：

现在就变成了这样，我们来对比一下红黑树：

不能说很像，只能说是一模一样啊。为什么呢？明明这两种树是不同的规则啊，为什么会出现等价的情况呢？

B树叶节点等深实际上体现在红黑树中为任一叶节点到达根节点的路径中，黑色路径所占的长度是相等的，因为黑色结点就是B树的结点分割值。

B树节点的键值数量不能超过N实际上体现在红黑树约定相邻红色结点接最多2条，也就是说不可能出现B树中元素超过3的情况，因为是4阶B树。

所以说红黑树跟4阶B树是有一定渊源的，甚至可以说它就是4阶B树的变体。

前面我们介绍了B树，现在我们就可以利用B树来高效存储数据了，当然我们还可以让它的查找效率更高。这里我们就要提到B+树了，B+树是B树的一种变体，有着比B树更高的查询性能。

有k个子树的中间结点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引，所有数据（卫星数据，就是具体需要保存的内容）都保存在叶子结点。
所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点按照从小到大的顺序连接。
所有的根结点元素都同时存在于子结点中，在子节点元素中是最大（或最小）元素。

我们来看看一棵B+树长啥样：

其中最后一层形成了一个有序链表，在我们需要顺序查找时，提供了极大的帮助。可以看到现在除了最后一层之外，其他结点中存放的值仅仅充当了一个指路人的角色，来告诉你你需要的数据在哪一边，比如根节点有10和18，因为这里是取得最大值，那么整棵树最大的元素就是18了，我们现在需要寻找一个小于18大于10的数，就可以走右边去查找。而具体的数据会放到最下面的叶子结点中，比如数据库就是具体的某一行数据（卫星数据）存放在最下面：

当然，目前可能你还没有接触过数据库，在以后的学习中，你一定会接触到它的，到时你就会发现新世界。

它不像B树那样，B树并不是只有最后一行会存储卫星数据，此时比较凌乱。因为只有最后一行存储卫星数据，使用B+树，同样大小的磁盘页可以容纳更多的节点元素，这就意味着，数据量相同的情况下B+树比B树高度更低，减小磁盘IO的次数。其次，B+树的查询必须最终查找到叶子节点，而B树做的是值匹配，到达结点之后并不一定能够匹配成功，所以B树的查找性能并不稳定，最好的情况是只查根节点即可，而最坏的情况则需要查到叶子节点，但是B+树每一次查找都是稳定的，因为一定在叶子结点。

并且得益于最后一行的链表结构，B+树在做范围查询时性能突出。很多数据库都在采用B+树作为底层数据结构，比如MySQL就默认选择B+Tree作为索引的存储数据结构。

至此，有关B树和B+树相关内容，就到这里。

哈夫曼树

最后我们来介绍一个比较重要的的树形结构，在开篇之前，我想问下，各位了解文件压缩吗？它是怎么做到的呢？我们都会在这一节进行探讨。

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树（Huffman Tree）

乍一看好像没看懂，啥叫带权路径长度达到最小？就是树中所有的叶结点的权值乘上其到根结点根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ItHxpKin-1683974335157)(null)]

这里我们分别将叶子结点ABCD都赋予一个权值，我们来尝试计算一下，计算公式如下：
$\sum_{i=1}^{n} (value(i) \times depth(i))$
那么左右两边的计算结果为：

左图： $WPL=5\times2+7\times2+2\times2+13\times2=54$
右图： $WPL=5\times3+2\times3+7\times2+13\times1=48$

通过计算结果可知，右图的带权路径长度最小，实际上右图是一棵哈夫曼树。

那么现在给了我们这些带权的叶子结点，我们怎么去构建一颗哈夫曼树呢？首先我们可以将这些结点视为4棵树，他们共同构成了一片森林：

首先我们选择两棵权值最小的树作为一颗新的树的左右子树，左右顺序不重要（因为哈夫曼编码不唯一，后面会说），得到的树根结点权值为这两个结点之和：

接着，我们需要将这这棵树放回到森林中，重复上面的操作，继续选择两个最小的出来组成一颗新的树，此时得到：

继续重复上述操作，直到森林里面只剩下一棵树为止：

这样，我们就得到了一棵哈夫曼树，因为只要保证越大的值越靠近根结点，那么出来的一定是哈夫曼树。所以，我们辛辛苦苦把这棵树构造出来干嘛呢？实际上哈夫曼树的一个比较重要应用就是对数据进行压缩，它是现代压缩算法的基础，我们常常可以看到网上很多文件都是以压缩包（.zip、.7z、.rar等格式）形式存在的，我们将文件压缩之后。

比如这一堆字符串：ABCABCD，现在我们想要将其进行压缩然后保存到硬盘上，此时就可以使用哈夫曼编码。那么怎么对这些数据进行压缩呢？这里我们就可以采用刚刚构建好的哈夫曼树，我们需要先对其进行标注：

向左走是0，向右走是1，比如现在我们要求出A的哈夫曼编码，那么就是根结点到A整条路径上的值拼接：

A：110
B：0
C：111
D：10

这些编码看起来就像二进制的一样，也便于我们计算机的数据传输和保存，现在我们要对上面的这个字符串进行压缩，那么只需要将其中的每一个字符翻译为对应编码就行了：

ABCABCD = 110 0 111 110 0 111 10

这样我们就得到了一堆压缩之后的数据了。那怎么解码回去呢，也很简单，只需要对照着写回去就行了：

110 0 111 110 0 111 10 = ABCABCD

我们来尝试编写一下代码实现一下哈夫曼树的构建和哈夫曼编码的获取把，因为构建哈夫曼树需要选取最小的两个结点，这里需要使用到优先级队列。

优先级队列与普通队列不同，它允许VIP插队（权值越大的元素优先排到前面去），当然出队还是一律从队首出来。

比如一开始4和9排在队列中，这时又来了个7，那么由于7比4大，所以说可以插队，直接排到4的前面去，但是由于9比7大，所以说不能再往前插队了：

这就是优先级队列，VIP插队机制，要实现这样的优先级队列，我们只需要修改一下入队操作即可：

_Bool initQueue(LinkedQueue queue){
    LNode node = malloc(sizeof(struct LNode));
    if(node == NULL) return 0;
    queue->front = queue->rear = node;
    node->next = NULL;   //因为下面用到了判断结点的下一个为NULL，所以说记得默认设定为NULL
    return 1;
}

_Bool offerQueue(LinkedQueue queue, T element){
    LNode node = malloc(sizeof(struct LNode));
    if(node == NULL) return 0;
    node->element = element;
  	node->next = NULL;   //因为下面用到了判断结点的下一个为NULL，所以说记得默认设定为NULL
    LNode pre = queue->front;   //我们从头结点开始往后挨个看，直到找到第一个小于当前值的结点，或者到头为止
    while (pre->next && pre->next->element >= element)
        pre = pre->next;
    if(pre == queue->rear) {   //如果说找到的位置已经是最后了，那么直接插入就行，这里跟之前是一样的
        queue->rear->next = node;
        queue->rear = node;
    } else {    //否则开启VIP模式，直接插队
        node->next = pre->next;
        pre->next = node;
    }
    return 1;
}

我们来测试一下吧：

int main(){
    struct Queue queue;
    initQueue(&queue);

    offerQueue(&queue, 9);
    offerQueue(&queue, 4);
    offerQueue(&queue, 7);
    offerQueue(&queue, 3);
    offerQueue(&queue, 13);

    printQueue(&queue);
}

这样我们就编写好了一个优先级队列，然后就可以开始准备构建哈夫曼树了：

typedef char E;

typedef struct TreeNode {
    E element;
    struct TreeNode * left;
    struct TreeNode * right;
    int value;    //存放权值
} * Node;

首先按照我们前面的例子，构建出这四个带权值的结点：

Node createNode(E element, int value){   //创建一个结点
    Node node = malloc(sizeof(struct TreeNode));
    node->element = element;
    node->left = node->right = NULL;
    node->value = value;
    return node;
}

_Bool offerQueue(LinkedQueue queue, T element){
    LNode node = malloc(sizeof(struct LNode));
    if(node == NULL) return 0;
    node->element = element;
  	node->next = NULL;
    LNode pre = queue->front;
    while (pre->next && pre->next->element->value <= element->value)   //注意这里改成权重的比较，符号改成小于
        pre = pre->next;
    if(pre == queue->rear) {
        queue->rear->next = node;
        queue->rear = node;
    } else {
        node->next = pre->next;
        pre->next = node;
    }
    return 1;
}

现在我们来测试一下吧：

int main(){
    struct Queue queue;
    initQueue(&queue);

    offerQueue(&queue, createNode('A', 5));
    offerQueue(&queue, createNode('B', 16));
    offerQueue(&queue, createNode('C', 8));
    offerQueue(&queue, createNode('D', 13));

    printQueue(&queue);
}

已经是按照权重顺序在排队了，接着我们就可以开始构建哈夫曼树了：

int main(){
    struct Queue queue;
    initQueue(&queue);

    offerQueue(&queue, createNode('A', 5));
    offerQueue(&queue, createNode('B', 16));
    offerQueue(&queue, createNode('C', 8));
    offerQueue(&queue, createNode('D', 13));

    while (queue.front->next != queue.rear) {   //如果front的下一个就是rear那么说明队列中只有一个元素了
        Node left = pollQueue(&queue);
        Node right = pollQueue(&queue);
        Node node = createNode(' ', left->value + right->value);   //创建新的根结点
        node->left = left;
        node->right = right;
        offerQueue(&queue, node);   //最后将构建好的这棵树入队
    }

    Node root = pollQueue(&queue);   //最后出来的就是哈夫曼树的根结点了
}

现在得到哈夫曼树之后，我们就可以对这些字符进行编码了，当然注意我们这里面只有ABCD这几种字符：

char * encode(Node root, E e){
    if(root == NULL) return NULL;   //为NULL肯定就是没找到
    if(root->element == e) return "";   //如果找到了就返回一个空串
    char * str = encode(root->left, e);  //先去左边找
    char * s = malloc(sizeof(char) * 10);
    if(str != NULL) {
        s[0] = '0';
        str = strcat(s, str);   //如果左边找到了，那么就把左边的已经拼好的字符串拼接到当前的后面
    } else {    //左边不行那再看看右边
        str = encode(root->right, e);
        if(str != NULL) {
            s[0] = '1';
            str = strcat(s, str);   //如果右边找到了，那么就把右边的已经拼好的字符串拼接到当前的后面
        }
    }
    return str;   //最后返回操作好的字符串给上一级
}

void printEncode(Node root, E e){
    printf("%c 的编码为：%s", e, encode(root, e));   //编码的结果就是了
    putchar('\n');
}

最后测试一下吧：

int main(){
    struct Queue queue;
    initQueue(&queue);

    ...
      
    Node root = pollQueue(&queue);
    printEncode(root, 'A');
    printEncode(root, 'B');
    printEncode(root, 'C');
    printEncode(root, 'D');
}

成功得到对应的编码：

堆和优先级队列

前面我们在讲解哈夫曼树时了解了优先级队列，它提供一种可插队的机制，允许权值大的结点排到前面去，但是出队顺序还是从队首依次出队。我们通过对前面的队列数据结构的插入操作进行改造，实现了优先级队列。

这节课我们接着来了解一下堆（Heap）它同样可以实现优先级队列。

首先必须是一棵完全二叉树，树中父亲都比孩子小的我们称为小根堆（小顶堆），树中父亲都比孩子大则是大根堆（注意不要跟二叉查找树搞混了，二叉查找树是左小右大，而堆只要是孩子一定小或者大），它是一颗具有特殊性质的完全二叉树。比如下面就是一个典型的大根堆：

因为完全二叉树比较适合使用数组才存储（因为是按序的）所以说一般堆都是以数组形式存放：

那么它是怎么运作的呢？比如现在我们想要往堆中插入一个新的元素8，那么：

因为是一棵完全二叉树，那么必须按照顺序，继续在当前这一行从左往右插入新的结点，其实就相当于在数组的后面继续加一个新的进来，是一样的。但是因为要满足大顶堆的性质，所以此时8加入之后，破坏了规则，我们需要进行对应的调整（堆化），很简单，我们只需要将其与父结点交换即可：

同样的，数组的形式的话，我们就行先计算出它的父结点，然后进行交换即可：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-an65FBNd-1683974333410)(null)]

当然，还没完，我们还需要继续向上比较，直到稳定为止，此时7依然是小于8的，所以说需要继续交换：

现在满足性质了，堆化结束，可以看到最大的元素被排到了最前面，这不就是我们前面的优先级队列吗。

现在我们来试试看删除队首元素，也就相当于出队操作，删除最顶上的元素：

现在需要删除最顶上的元素但是我们需要保证删除之后依然是一棵完全二叉树，所以说我们先把排在最后面的拿上来顶替一下：

接着我们需要按照与插入相反的方向，从上往下进行堆化操作，规则是一样的，遇到大的就交换，直到不是为止：

这样，我们发现，即使完成了出队操作，依然是最大的元素排在队首，并且整棵树依然是一棵完全二叉树。

按照上面的操作，我们来编写一下代码吧，这里还是以大顶堆为例：

typedef int E;
typedef struct MaxHeap {
    E * arr;
    int size;
    int capacity;
} * Heap;

_Bool initHeap(Heap heap){   //初始化都是老套路了，不多说了
    heap->size = 0;
    heap->capacity = 10;
    heap->arr = malloc(sizeof (E) * heap->capacity);
    return heap->arr != NULL;
}

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
}

接着就是插入操作，首先还是需要判断是否已满：

_Bool insert(Heap heap, E element){
    if(heap->size == heap->capacity) return 0;   //满了就不处理了，主要懒得写扩容了
    int index = ++heap->size;   //先计算出要插入的位置，注意要先自增，因为是从1开始的
    //然后开始向上堆化，直到符合规则为止
    while (index > 1 && element > heap->arr[index / 2]) {
        heap->arr[index] = heap->arr[index / 2];
        index /= 2;
    }
    //现在得到的index就是最终的位置了
    heap->arr[index] = element;
    return 1;
}

我们来测试一下吧：

void printHeap(Heap heap){
    for (int i = 1; i <= heap->size; ++i)
        printf("%d ", heap->arr[i]);
}

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
    insert(&heap, 5);
    insert(&heap, 2);
    insert(&heap, 3);
    insert(&heap, 7);
    insert(&heap, 6);

    printHeap(&heap);
}

最后结果为：

插入完成之后，我们接着来写一下删除操作，删除操作实际上就是出队的操作：

E delete(Heap heap){
    E max = heap->arr[1], e = heap->arr[heap->size--];
    int index = 1;
    while (index * 2 <= heap->size) {   //跟上面一样，开找，只不过是从上往下找
        int child = index * 2;   //先找到左孩子
        //看看右孩子和左孩子哪个大，先选一个大的出来
        if(child < heap->size && heap->arr[child] < heap->arr[child + 1])
            child += 1;
        if(e >= heap->arr[child]) break;   //如果子结点都不大于新结点，那么说明就是这个位置，结束就行了
        else heap->arr[index] = heap->arr[child];  //否则直接堆化，换上去
        index = child;   //最后更新一下index到下面去
    }
    heap->arr[index] = e;   //找到合适位置后，放进去就行了
    return max;
}

最后我们来测试一下吧：

int main(){
    struct MaxHeap heap;
    initHeap(&heap);
    ...
    for (int i = 0; i < 5; ++i) {
        printf("%d ", delete(&heap));
    }
}

可以看到结果就是优先级队列的出队结果，这样，我们就编写好了大顶堆的插入和删除操作了。

当然，堆在排序上也有着非常方便的地方，在后面的排序算法篇中，我们还会再次说起它。

至此，有关树形结构篇的内容，我们就全部讲解完毕了，请务必认真掌握前面的二叉树和高级二叉树结构，这些都是重点内容，下一章我们将继续探讨散列表。

算法实战

二叉树相关的算法实战基本都是与递归相关的，因为它实在是太适合用分治算法了！

（简单）二叉查找树的范围和

本题来自LeetCode：938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入：root = [10,5,15,3,7,null,18], low = 7, high = 15 （注意力扣上的输入案例写的是层序序列，含空节点）
输出：32

示例 2：

输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

这道题其实就是考察我们对于二叉查找树的理解，利用二叉查找树的性质，这道题其实很简单，只需要通过递归分治就可以解决了。

代码如下：

int rangeSumBST(struct TreeNode* root, int low, int high){
    if(root == NULL) return 0;
    if(root->val > high)    //如果最大的值都比当前结点值小，那么肯定在左边才能找到
        return rangeSumBST(root->left, low, high);
    else if(root->val < low)   //如果最小值都比当前结点大，那么肯定在右边才能找到
        return rangeSumBST(root->right, low, high);
    else
        //这种情况肯定是在范围内了，将当前结点值加上左右的，再返回
        return root->val + rangeSumBST(root->right, low, high) + rangeSumBST(root->left, low, high);
}

这种问题比较简单，直接四行就解决了。

（中等）重建二叉树

本题来自LeetCode：剑指 Offer 07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

实际上这道题就是我们前面练习题的思路，现在给到我们的是前序和中序遍历的结果，我们只需要像之前一样逐步推导即可。

在中序遍历序列中找到根节点的位置后，这个问题就很好解决了，大致思路如下：

由于前序遍历首元素为根节点值，首先可以得到根节点值。
在中序遍历序列中通过根节点的值，寻找根节点的位置。
将左右两边的序列分割开来，并重构为根节点的左右子树。（递归分治）
在新的序列中，重复上述步骤，通过前序遍历再次找到当前子树的根节点，再次进行分割。
直到分割到仅剩下一个结点时，开始回溯，从而完成整棵二叉树的重建。

解题代码如下：

struct TreeNode * createNode(int val){   //这个就是单纯拿来创建结点的函数
    struct TreeNode * node = malloc(sizeof(struct TreeNode));
    node->left = node->right = NULL;
    node->val = val;
    return node;
}

//核心递归分治实现
struct TreeNode* buildTreeCore(int * preorder, int * inorder, int start, int end, int index){
    if(start > end) return NULL;   //如果都超出范围了，肯定不行
    if(start == end) return createNode(preorder[index]);   //如果已经到头了，那么直接创建结点返回即可
    struct TreeNode * node = createNode(preorder[index]);   //先从前序遍历中找到当前子树的根结点值，然后创建对应的结点
    int pos = 0;   
    while (inorder[pos] != preorder[index]) pos++;   //找到中序的对应位置，从这个位置开始左右划分
    node->left = buildTreeCore(preorder, inorder, start, pos - 1, index+1);   
  	//当前结点的左子树按照同样的方式建立
  	//因为前序遍历的下一个结点就是左子树的根结点，所以说这里给index+1
    node->right = buildTreeCore(preorder, inorder, pos+1, end, index+(pos-start)+1);  
  	//当前结点的右子树按照同样的方式建立
  	//最后一个index需要先跳过左子树的所有结点，才是右子树的根结点，所以说这里加了个pos-start，就是中序划分出来，左边有多少就减去多少
    return node;   //向上一级返回当前结点
}

struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
    return buildTreeCore(preorder, inorder, 0, preorderSize - 1, 0);
  	//这里传入了前序和中序序列，并且通过start和end指定当前中序序列的处理范围，最后的一个index是前序遍历的对应头结点位置
}

（中等）验证二叉搜索树

本题来自LeetCode：98. 验证二叉搜索树（先说，这题老六行为过多，全站通过率只有36.5%，但是题目本身很简单）

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

这种题看起来好像还挺简单的，我们可以很快地写出代码：

bool isValidBST(struct TreeNode* root){
    if(root == NULL) return true;   //到头了就直接返回真
    if(root->left != NULL && root->left->val >= root->val) return false;  //如果左边不是空，并且左边还比当前结点值小的话，那肯定不是了
    if(root->right != NULL && root->right->val <= root->val) return false;  //同上
    return isValidBST(root->left) && isValidBST(root->right);  //接着向下走继续判断左右两边子树，必须同时为真才是真
}

然后直接上力扣测试，嗯，没问题，提交，这把必过！于是光速打脸：

不可能啊，我们的逻辑判断没有问题的，我们的算法不可能被卡的啊？（这跟我当时打ACM一样的感觉，我这天衣无缝的算法不可能错的啊，哪个老六测试用例给我卡了）这其实是因为我们没有考虑到右子树中左子树比根结点值还要小的情况：

虽然这样错的很明显，但是按照我们上面的算法，这种情况确实也会算作真。所以说我们需要改进一下，对其上界和下界进行限定，不允许出现这种低级问题：

bool isValid(struct TreeNode* root, long min, long max){   //这里上界和下界用long表示，因为它的范围给到整个int，真是个老六
    if(root == NULL) return true;
    //这里还需要判断是否正常高于下界
    if(root->left != NULL && (root->left->val >= root->val || root->left->val <= min))
        return false;
    //这里还需判断一下是否正常低于上界
    if(root->right != NULL && (root->right->val <= root->val || root->right->val >= max))
        return false;
    return isValid(root->left, min, root->val) && isValid(root->right, root->val, max);
    //注意往左走更新上界，往右走更新下界
}

bool isValidBST(struct TreeNode* root){
    return isValid(root, -2147483649, 2147483648);   //下界刚好比int少1，上界刚好比int多1
}

这样就没问题了。

（中等）求根到叶数字之和

本题来自LeetCode：129. 求根节点到叶节点数字之和

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的所有数字之和。

叶节点是指没有子节点的节点。

示例 1：

输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WiDXr7C6-1683974307777)(null)]

输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

这道题其实也比较简单，直接从上向下传递当前路径上已经组装好的值即可，到底时返回最终的组装结果：

int sumNumbersImpl(struct TreeNode * root, int parent){
    if(root == NULL) return 0;   //如果到头了，直接返回0
  	int sum = root->val + parent * 10;   //因为是依次向后拼接，所以说直接将之前的值x10然后加上当前值即可
    if(!root->left && !root->right)    //如果是叶子结点，那么直接返回结果
        return sum;
  	//否则按照同样的方式将左右的结果加起来
    return sumNumbersImpl(root->left, sum) + sumNumbersImpl(root->right,  sum);
}

int sumNumbers(struct TreeNode* root){
    return sumNumbersImpl(root, 0);
}

（困难）结点之和的最大路径

本题来自LeetCode：剑指 Offer II 051. 节点之和最大的路径（这是一道Hard难度的题目，但是其实还好）

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。

路径和是路径中各节点值的总和。

给定一个二叉树的根节点 root ，返回其最大路径和，即所有路径上节点值之和的最大值。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

首先，我们要知道，路径有很多种可能，要么从上面下来，要么从左边上来往右边走，要么只走右边，要么只走左边…我们需要寻找一个比较好的方法在这么多种可能性之间选择出最好的那一个。

int result = -2147483648;    //使用一个全局变量来存储一下当前的最大值
int max(int a, int b){   //不想多说了
    return a > b ? a : b;
}

int maxValue(struct TreeNode* root){
    if(root == NULL) return 0;
    //先把左右两边走或是不走的情况计算一下，取出值最大的情况
    int leftMax = max(maxValue(root->left), 0);
    int rightMax = max(maxValue(root->right), 0);
    //因为要么只走左边，要么只走右边，要么左右都走，所以说我们计算一下最大情况下的结果
    int maxTmp = leftMax + rightMax + root->val;
    result = max(maxTmp, result);   //更新一下最大值
    //然后就是从上面下来的情况了，从上面下来要么左要么右，此时我们只需要返回左右最大的一个就行了
    return max(leftMax, rightMax) + root->val;  //注意还要加上当前结点的值，因为肯定要经过当前结点
}

int maxPathSum(struct TreeNode* root){
    maxValue(root);
    return result;   //最后返回完事之后最终得到的最大值
}

这样，我们就成功解决了这种问题。

散列表篇

在之前，我们已经学习了多种查找数据的方式，比如最简单的，如果数据量不大的情况下，我们可以直接通过顺序查找的方式在集合中搜索我们想要的元素；当数据量较大时，我们可以使用二分搜索来快速找到我们想要的数据，不过需要要求数据按照顺序排列，并且不允许中途对集合进行修改。

在学习完树形结构篇之后，我们可以利用二叉查找树来建立一个便于我们查找的树形结构，甚至可以将其优化为平衡二叉树或是红黑树来进一步提升稳定性。在最后我们还了解了B树和B+树，得益于它们的巧妙设计，我们可以以尽可能少的时间快速找到我们需要的元素，大大提升程序的运行效率。

这些都能够极大地帮助我们查找数据，而散列表，则是我们查找系列内容的最后一块重要知识。

散列查找

我们之前认识的查找算法，最快可以达到对数阶 $O (l o g N)$ ，那么我们能否追求极致，让查找性能突破到常数阶呢？这里就要介绍到我们的散列（也可以叫哈希 Hash）它采用直接寻址的方式，在理想情况下，查找的时间复杂度可以达到常数阶 $O (1)$ 。

散列（Hashing）通过散列函数（哈希函数）将要参与检索的数据与散列值（哈希值）关联起来，生成一种便于搜索的数据结构，我们称其为散列表（哈希表），也就是说，现在我们需要将一堆数据保存起来，这些数据会通过哈希函数进行计算，得到与其对应的哈希值，当我们下次需要查找这些数据时，只需要再次计算哈希值就能快速找到对应的元素了：

当然，如果一脸懵逼没关系，我们从哈希函数开始慢慢介绍。

散列函数

散列函数也叫哈希函数，哈希函数可以对一个目标计算出其对应的哈希值，并且，只要是同一个目标，无论计算多少次，得到的哈希值都是一样的结果，不同的目标计算出的结果介乎都不同。哈希函数在现实生活中应用十分广泛，比如很多下载网站都提供下载文件的MD5码校验，可以用来判别文件是否完整，哈希函数多种多样，目前应用最为广泛的是SHA-1和MD5，比如我们在下载IDEA之后，会看到有一个验证文件SHA-256校验和的选项，我们可以点进去看看：

点进去之后，得到：

e54a026da11d05d9bb0172f4ef936ba2366f985b5424e7eecf9e9341804d65bf *ideaIU-2022.2.1.dmg

这一串由数字和小写字母随意组合的一个字符串，就是安装包文件通过哈希算法计算得到的结果，那么这个东西有什么用呢？我们的网络可能有时候会出现卡顿的情况，导致我们下载的文件可能会出现不完整的情况，因为哈希函数对同一个文件计算得到的结果是一样的，我们可以在本地使用同样的哈希函数去计算下载文件的哈希值，如果与官方一致，那么就说明是同一个文件，如果不一致，那么说明文件在传输过程中出现了损坏。

可见，哈希函数在这些地方就显得非常实用，在我们的生活中起了很大的作用，它也可以用于布隆过滤器和负载均衡等场景，这里不多做介绍了。

散列表

前面我们介绍了散列函数，我们知道可以通过散列函数计算一个目标的哈希值，那么这个哈希值计算出来有什么用呢，对我们的程序设计有什么意义呢？我们可以利用哈希值的特性，设计一张全新的表结构，这种表结构是专为哈希设立的，我们称其为哈希表（散列表）

我们可以将这些元素保存到哈希表中，而保存的位置则与其对应的哈希值有关，哈希值是通过哈希函数计算得到的，我们只需要将对应元素的关键字（一般是整数）提供给哈希函数就可以进行计算了，一般比较简单的哈希函数就是取模操作，哈希表长度是多少（长度最好是一个素数），模就是多少：

比如现在我们需要插入一个新的元素（关键字为17）到哈希表中：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RSR8XUWF-1683974308690)(null)]

插入的位置为计算出来的哈希值，比如上面是8，那么就在下标位置8插入元素，同样的，我们继续插入27：

这样，我们就可以将多种多样的数据保存到哈希表中了，注意保存的数据是无序的，因为我们也不清楚计算完哈希值最后会放到哪个位置。那么如果现在我们想要从哈希表中查找数据呢？比如我们现在需要查找哈希表中是否有14这个元素：

同样的，直接去看哈希值对应位置上看看有没有这个元素，如果没有，那么就说明哈希表中没有这个元素。可以看到，哈希表在查找时只需要进行一次哈希函数计算就能直接找到对应元素的存储位置，效率极高。

我们可以通过代码来实现一下：

#define SIZE 9

typedef struct Element {   //这里用一个Element将值包装一下
    int key;    //这里元素设定为int
} * E;

typedef struct HashTable{   //这里把数组封装为一个哈希表
    E * table;
} * HashTable;

int hash(int key){   //哈希函数
    return key % SIZE;
}

void init(HashTable hashTable){   //初始化函数
    hashTable->table = malloc(sizeof(struct Element) * SIZE);
    for (int i = 0; i < SIZE; ++i)
        hashTable->table[i] = NULL;
}

void insert(HashTable hashTable, E element){   //插入操作，为了方便就不考虑装满的情况了
    int hashCode = hash(element->key);   //首先计算元素的哈希值
    hashTable->table[hashCode] = element;   //对号入座
}

_Bool find(HashTable hashTable, int key){
    int hashCode = hash(key);   //首先计算元素的哈希值
    if(!hashTable->table[hashCode]) return 0;   //如果为NULL那就说明没有
    return hashTable->table[hashCode]->key == key;  //如果有，直接看是不是就完事
}

E create(int key){    //创建一个新的元素
    E e = malloc(sizeof(struct Element));
    e->key = key;
    return e;
}

int main() {
    struct HashTable hashTable;
    init(&hashTable);
    insert(&hashTable, create(10));
    insert(&hashTable, create(7));
    insert(&hashTable, create(13));
    insert(&hashTable, create(29));

    printf("%d\n", find(&hashTable, 1));
    printf("%d\n", find(&hashTable, 13));
}

这样，我们就实现了一个简单的哈希表和哈希函数，通过哈希表，我们可以将数据的查找时间复杂度提升到常数阶。

哈希冲突

前面我介绍了哈希函数，通过哈希函数计算得到一个目标的哈希值，但是在某些情况下，哈希值可能会出现相同的情况：

比如现在同时插入14和23这两个元素，他们两个计算出来的哈希值是一样的，都需要在5号下标位置插入，这时就出现了打架的情况，那么到底是把哪一个放进去呢？这种情况，我们称为哈希碰撞（哈希冲突）

这种问题是很严重的，因为哈希函数的设计不同，难免会出现这种情况，这种情况是不可避免的，我们只能通过使用更加高级的哈希函数来尽可能避免这种情况，但是无法完全避免。当然，如果要完全解决这种问题，我们还需要去寻找更好的方法。

线性探测法

既然有可能出现哈希值重复的情况，那么我们可以选择退让，不去进行争抢（忍一时风平浪静，退一步海阔天空）我们可以去找找哈希表中相邻的位置上有没有为空的，只要哈希表没装满，那么我们肯定是可以找到位置装下这个元素的，这种类型的解决方案我们统称为线性探测法，开放定址法包含，线性探测法、平方探测法、双散列法等，这里我们以线性探测法为例。

既然第一次发生了哈希冲突，那么我们就继续去找下一个空位：
$h_i(key) = (h(key) + d_i)\space \% \space TableSize$
其中 $d_i$ 是随着哈希冲突次数增加随之增加的量，比如上面出现了一次哈希冲突，那么我就将其变成1表示发生了一次哈希冲突，然后我们可以继续去寻找下一个位置：

出现哈希冲突时， $d_i$ 自增，继续寻找下一个空位：

再次计算哈希值，成功得到对应的位置，注意 $d_i$ 默认为0，这样我们就可以解决冲突的情况了。

我们来通过代码实际使用一下，这里需要调整一下插入和查找操作的逻辑：

void insert(HashTable hashTable, E element){   //插入操作，注意没考虑满的情况，各位小伙伴可以自己实现一下
    int hashCode = hash(element->key), count = 0;
    while (hashTable->table[hashCode]) {   //如果发现哈希冲突，那么需要继续寻找
        hashCode = hash(element->key + ++count);
    }
    hashTable->table[hashCode] = element;   //对号入座
}

_Bool find(HashTable hashTable, int key){
    int hashCode = hash(key), count = 0;   //首先计算元素的哈希值
    const int startIndex = hashCode;   //记录一下起始位置，要是转一圈回来了得停
    do {
        if(hashTable->table[hashCode]->key == key) return 1;  //如果找到就返回1
        hashCode = hash(key + ++count);
    } while (startIndex != hashCode && hashTable->table[hashCode]);  //没找到继续找
    return 0;
}

这样当出现哈希冲突时，会自动寻找补位插入：

int main() {
    struct HashTable hashTable;
    init(&hashTable);
    for (int i = 0; i < 9; ++i) {
        insert(&hashTable, create(i * 9));
    }

    for (int i = 0; i < 9; ++i) {
        printf("%d ", hashTable.table[i]->key);
    }
}

当然，如果采用这种方案删除会比较麻烦，因为有些元素可能是通过线性探测补到其他位置上的，如果删除元素，那么很有可能会影响到前面的查找操作：

此时删除关键字为45的元素，会出现截断的情况，当下次查找时，会出现严重问题：

可以看到，删除一个元素可能会导致原有的结构意外截断，无法正确找到对应的元素，所以，我们在删除元素时，为了防止出现这种截断的情况，我们需要对这个位置进行标记，表示之前有过元素，但是被删除了，当我们在查找时，如果发现曾经有过元素，依然需要继续向后寻找：

代码实现有点麻烦，这里就不编写代码了。

当然除了直接向后进行探测之外，我们也可以采用二次探测再散列法处理哈希冲突，因为有些时候可能刚好后面没有空位了，但是前面有，如果按照之前的方法，我们得转一圈回来才能找到对应的位置，实在是有点浪费时间，所以说我们可以左右开弓，同时向两个方向去寻找。

它的查找增量序列为： $1^2$ 、 $1^2$ 、 $2^2$ 、 $2^2$ 、…、 $q^2$ 、 $q^2$ ，其中 $\lfloor {TableSize\div2} \rfloor$ ，比如现在我们要向下面的哈希表中插入数据，现在插入关键字为24的元素，发现冲突了：

那么此时就需要进行处理了，这里我们采用上面的方式，先去寻找 $1^2$ 位置：

我们接着来插入：

实际上我们发现和之前是一样的，只要冲突就一直往下找就完事，只不过现在是左右横跳着找，这样可以进一步提升利用率。

链地址法

实际上常见的哈希冲突解决方案是链地址法，当出现哈希冲突时，我们依然将其保存在对应的位置上，我们可以将其连接为一个链表的形式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LSYn3ntG-1683974297443)(…/…/…/…/nagocoler/Library/Application Support/typora-user-images/image-20220820220237535.png)]

当表中元素变多时，差不多就变成了这样，我们一般将其横过来看：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LIzvMplk-1683974297444)(…/…/…/…/nagocoler/Library/Application Support/typora-user-images/image-20220820221104298.png)]

通过结合链表的形式，哈希冲突问题就可以得到解决了，但是同时也会出现一定的查找开销，因为现在有了链表，我们得挨个往后看才能找到，当链表变得很长时，查找效率也会变低，此时我们可以考虑结合其他的数据结构来提升效率。比如当链表长度达到8时，自动转换为一棵平衡二叉树或是红黑树，这样就可以在一定程度上缓解查找的压力了。

我们来编写代码尝试一下：

#define SIZE 9

typedef struct ListNode {   //结点定义
    int key;
    struct ListNode * next;
} * Node;

typedef struct HashTable{   //哈希表
    struct ListNode * table;   //这个数组专门保存头结点
} * HashTable;

void init(HashTable hashTable){
    hashTable->table = malloc(sizeof(struct ListNode) * SIZE);
    for (int i = 0; i < SIZE; ++i) {
        hashTable->table[i].key = -1;   //将头结点key置为-1，next指向NULL
        hashTable->table[i].next = NULL;
    }
}

int main(){
    struct HashTable table;    //创建哈希表
    init(&table);
}

接着是编写对应的插入操作，插入后直接往链表后面丢就完事了：

int hash(int key){   //哈希函数
    return key % SIZE;
}

Node createNode(int key){   //创建结点专用函数
    Node node = malloc(sizeof(struct ListNode));
    node->key = key;
    node->next = NULL;
    return node;
}

void insert(HashTable hashTable, int key){
    int hashCode = hash(key);
    Node head = hashTable->table + hashCode;   //先计算哈希值，找到位置后直接往链表后面插入结点就完事了
    while (head->next) head = head->next;
    head->next = createNode(key);   //插入新的结点
}

同样的，查找的话也是直接找到对应位置，看看链表里面有没有就行：

_Bool find(HashTable hashTable, int key){
    int hashCode = hash(key);
    Node head = hashTable->table + hashCode;
    while (head->next && head->key != key)   //直到最后或是找到为止
        head = head->next;
    return head->key == key;   //直接返回是否找到
}

我们来测试一下吧：

int main(){
    struct HashTable table;
    init(&table);

    insert(&table, 10);
    insert(&table, 19);
    insert(&table, 20);

    printf("%d\n", find(&table, 20));
    printf("%d\n", find(&table, 17));
    printf("%d\n", find(&table, 19));
}

实际上这种方案代码写起来也会更简单，使用也更方便一些。

散列表习题：

下面关于哈希查找的说法，正确的是（）

A 哈希函数构造的越复杂越好，因为这样随机性好，冲突小

B 除留余数法是所有哈希函数中最好的

C 不存在特别好与坏的哈希函数，要视情况而定

D 越简单的哈希函数越容易出现冲突，是最坏的

首先，衡量哈希函数好坏并没有一个确切的标准，而是需要根据具体情况而定，并不一定复杂的哈希函数就好，因为会带来时间上的损失。其实我们的生活中很多东西都像这样，没有好坏之分，只有适不适合的说法，所以说选择C选项
设有一组记录的关键字为{19，14，23，1，68，20，84，27，55，11，10，79}，用链地址法构造散列表，散列函数为H（key）=key MOD 13,散列地址为1的链中有（）个记录。

A 1 B 2 C 3 D 4

这种咱们得画图才知道了，答案是D
设哈希表长为14，哈希函数是H(key)=key%11，表中已有数据的关键字为15，38，61，84共四个，现要将关键字为49的元素加到表中，用二次探测再散列解决冲突，则放入的位置是（）

A 8 B 3 C 5 D 9

咱们先把这个表给画出来吧，答案是D
选取哈希函数 H(key)=(key x 3)%11 用线性探测散列法和二次探测再散列法分别处理冲突。试在0~10的散列地址空间中，对关键字序列（22,41,53,46,30,13,1,67）构建哈希表，并求等概率情况下查找成功的平均查找长度。

其中平均查找长度（ASL）就是表中每一个元素需要查找次数之和的平均值，我们注意在插入元素时顺便记录计算次数即可，如果是链地址法，那么直接看层数就行，ASL =（第一层结点数量+第二层结点数量+第三层结点数量）/ 非头结点总数

算法实战

（简单）两数之和

本题来自LeetCode：1.两数之和（整个力扣的第一题）

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

这道题很简单，实际上使用暴力枚举是可以完成的，我们只需要让每个数去寻找一个与其匹配的数即可，所以说直接循环就完事：

int * result(int i, int j, int * returnSize){
    *returnSize = 2;
    int * result = malloc(sizeof(int) * 2);
    result[0] = i;
    result[1] = j;
    return result;
}

int* twoSum(int* nums, int numsSize, int target, int* returnSize){
    for (int i = 0; i < numsSize; ++i) {
        for (int j = 0; j < numsSize; ++j) {
            if(j == i) continue;
            if(nums[i] + nums[j] == target) 
                return result(i, j, returnSize);   //找到匹配就直接返回完事
        }
    }
    return NULL;   //无视即可，因为不可能
}

但是这样效率实在是太低了，可以看到我们的程序运行时间都好几百毫秒了，能不能优化一下呢？我们正好学习了散列表，是否可以利用一下散列表来帮助我们完成？

因为每当我们遍历一个数时，实际上就是去寻找与其匹配的数是否存在，我们可以每遍历一个数都将其存放到散列表中，当下次遇到与其相匹配的数时，只要能够从散列表中找到这个数，那么就可以直接完成匹配了，这样就只需要遍历一次即可完成。比如：

[2,7,11,15] ，targert = 9

第一次先将2放入散列表，接着往后看7，现在目标值时9，那么只需要去寻找 9 - 7 这个数，看看散列表中有没有即可，此时散列表中正好有2，所以说直接返回即可。

我们来尝试编写一下：

#define SIZE 128

typedef int K;
typedef int V;

typedef struct LNode {   //结点定义需要稍微修改一下，因为除了存关键字还需要存一下下标
    K key;
    V value;
    struct LNode * next;
} * Node;

typedef struct HashTable{   //哈希表
    struct LNode * table;   //这个数组专门保存头结点
} * HashTable;

void init(HashTable hashTable){
    hashTable->table = malloc(sizeof(struct LNode) * SIZE);
    for (int i = 0; i < SIZE; ++i) {
        hashTable->table[i].key = -1;   //将头结点key置为-1，value也变成-1，next指向NULL
        hashTable->table[i].value = -1;
        hashTable->table[i].next = NULL;
    }
}

int hash(unsigned int key){  //因为哈希表用的数组，要是遇到负数的key，肯定不行，咱先给它把符号扬了再算
    return key % SIZE;
}

Node create(K key, V value){   //创建结点，跟之前差不多
    Node node = malloc(sizeof(struct LNode));
    node->key = key;
    node->value = value;
    node->next = NULL;
    return node;
}

void insert(HashTable hashTable, K key, V value){
    int hashCode = hash(key);
    Node head = hashTable->table + hashCode;
    while (head->next) head = head->next;
    head->next = create(key, value);   //这里同时保存关键字和对应的下标
}

Node find(HashTable hashTable, K key){
    int hashCode = hash(key);
    Node head = hashTable->table + hashCode;     //直接定位到对应位置
    while (head->next && head->next->key != key)   //直接看有没有下一个结点，并且下一个结点不是key
        head = head->next;  //继续往后找
    return head->next;   //出来之后要么到头了下一个是NULL，要么就是找到了，直接返回
}

哈希表编写完成后，我们就可以使用了：

int * result(int i, int j, int * returnSize){   //跟上面一样
    *returnSize = 2;
    int * result = malloc(sizeof(int) * 2);
    result[0] = i;
    result[1] = j;
    return result;
}

int* twoSum(int* nums, int numsSize, int target, int* returnSize){
    struct HashTable table;    //初始化哈希表
    init(&table);
    for (int i = 0; i < numsSize; ++i) {   //挨个遍历
        Node node = find(&table, target - nums[i]);  //直接去哈希表里面寻找匹配的，如果有直接结束，没有就丢把当前的key丢进哈希表，之后如果遇到与其匹配的另一半，那么就直接成功了
        if(node != NULL) return result(i, node->value, returnSize);
        insert(&table, nums[i], i);
    }
    return NULL;   //无视就好
}

我们再次提交代码，时间直接来到了个位数：

采用哈希表，就是一种空间换时间的策略，在大多数情况下，我们也更推荐使用这种方案。

数据结构与算法基础知识

线性结构篇

什么是数据结构与算法

数据结构

算法

案例：二分搜索算法

线性表

顺序表

链表

双向链表和循环链表

特殊线性表

栈

队列

算法实战

（简单）删除链表中重复元素

（简单）反转链表

（中等）旋转链表

（简单）有效的括号

（简单）第 k 个缺失的正整数

树形结构篇

树与森林

树结构介绍

森林

二叉树

满二叉树和完全二叉树

树和森林的转换

二叉树的性质

二叉树的构建

二叉树的遍历

高级树结构

线索化二叉树

二叉查找树

平衡二叉树

红黑树

其他树结构

B树和B+树

哈夫曼树

堆和优先级队列

算法实战

（简单）二叉查找树的范围和

（中等）重建二叉树

（中等）验证二叉搜索树

（中等）求根到叶数字之和

（困难）结点之和的最大路径

散列表篇

散列查找

散列函数

散列表

哈希冲突

线性探测法

链地址法

算法实战

（简单）两数之和

你可能感兴趣的:(数据结构,数据结构)