二叉树的最近公共祖先节点
1.原生题目
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先
https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree
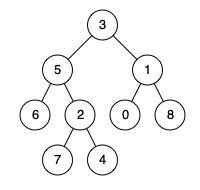
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
递归
思路分析:该题大致会出现四种情况:
- p,q节点均在左子树
- p,q节点均在右子树
- p,q不同时在一颗子树,直接返回root
- p或q节点等于root节点,此时直接返回root节点
则先对p,q节点进行寻找,在左子树还是右子树,再分别对上述情况进行递归判断。
class Solution {
public:
bool find(TreeNode* root, TreeNode* p)//寻找节点是否存在
{
if(root == nullptr)
return false;
if(root == p)
return true;
return find(root->left,p) || find(root->right,p);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
if(root == p || root == q)
return root;
bool pInleft,pInright,qInleft,qInright;
if(find(root->left,p))//p在左子树
{
pInleft = true;
pInright = false;
}
else//p在右子树
{
pInleft = false;
pInright = true;
}
if(find(root->left,q))//q在左子树
{
qInleft = true;
qInright = false;
}
else//q在右子树
{
qInleft = false;
qInright = true;
}
if(pInleft && qInleft)//同时在左
return lowestCommonAncestor(root->left,p,q);
if(pInright && qInright)//同时在右
return lowestCommonAncestor(root->right,p,q);
return root;//不在一边,直接返回root
}
};
递归改进
递归的本质是什么,使用递归可看成我们已经算出了结果。
还是上述的情况,对代码进行改进。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
if(root == p || root == q)
return root;
TreeNode* left = lowestCommonAncestor(root->left,p,q);//左边结果
TreeNode* right = lowestCommonAncestor(root->right,p,q);//右边结果
if(left == nullptr)//左边为空,返回右边
return right;
if(right == nullptr)//右边为空,返回左边
return left;
return root;//同时为空,返回根节点
}
};
2.二叉搜索树的最近公共祖先节点
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
链接:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree
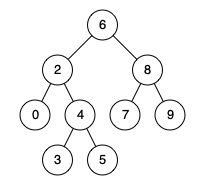
该题可用第一题直接提交,但没有利用到二叉搜索树的本质。
二叉搜索树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
利用其特性,即可快速的做出该题目:
思路分析:三种情况:
- p,q同时大于根节点,同时在右子树
- p,q同时小于根节点,同时在左子树
- p,q不在一颗子树上,即根为最近公共祖先节点,返回root
代码:
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(p->val > root->val && q->val > root->val)//同时在右子树
return lowestCommonAncestor(root->right,p,q);
if(p->val < root->val && q->val < root->val)//同时在左子树
return lowestCommonAncestor(root->left,p,q);
return root;//一左一右
}
};
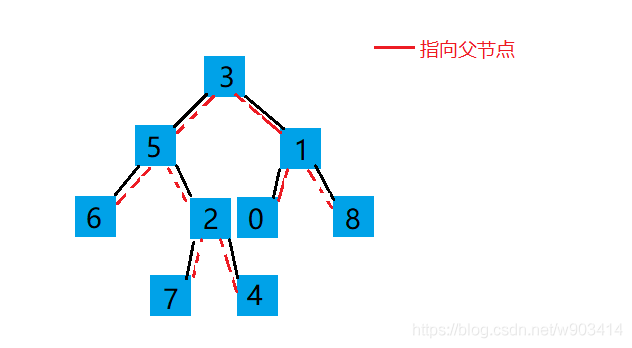
3.左右子树有一个指向父节点的指针
即:
比如:求7和4节点最近公共祖先节点,可以通过一步一步指向父节点去求。
于是该问题就转化成了求,两个链表相交的第一个公共节点。
链接:链表相交
4.题目变种
题目描述:
有一棵无穷大的满二叉树,其结点按根结点一层一层地从左往右依次编号,根结点编号为1。现在有两个结点a,b。请设计一个算法,求出a和b点的最近公共祖先的编号。给定两个int a,b。为给定结点的编号。请返回a和b的最近公共祖先的编号。注意这里结点本身也可认为是其祖先。
满二叉树:
测试样例:
2,3
返回: 1
重要信息:满二叉树,层序遍历,根节点编号为1
思路分析:因为是满二叉树,层序遍历,则根据其二叉树的性质:根节点编号为1时,叶子节点编号除2,就是其父节点。
该问题似乎又转化到了,上述有一个指向其父节点指针的题。
通过不断的除2,分别保存父节点的编号,找到两个下标编号第一次相同的,即找到了其父节点。
class Solution {
public:
int getP(int a, int b) {
vector<int> va;//储存a的父节点
vector<int> vb;//储存b的父节点
while (a)
{
va.push_back(a);
a /= 2;
}
while (b)
{
vb.push_back(b);
b /= 2;
}
int ret = 0;
size_t sza = va.size();
size_t szb = vb.size();
size_t sz = sza > szb ? szb : sza;
for (size_t i = sz - 1; i >= 0; --i)
{
if (va[sza - i - 1] == vb[szb - i - 1])//直接从短的第一个位置,长的相同位置开始搜索
{
ret = va[sza - i - 1];
break;
}
}
return ret;
}
};