【HuoLe的刷题笔记】--leetcode算法题
leetcode刷题记录
数组类:
简单题:
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap map = new HashMap<>();
for(int i = 0; i < nums.length; i++){
if(map.containsKey(target - nums[i])){
return new int[]{map.get(target - nums[i]), i};
}
map.put(nums[i],i);
}
return new int[]{-1,-1};
}
}
26. 删除有序数组中的重复项
给你一个有序数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
class Solution {
public int removeDuplicates(int[] nums) {
int index = 0;
for(int i = 0; i < nums.length-1; i++){
if(nums[i] != nums[i+1]){
nums[index] = nums[i];
index++;
nums[index] = nums[i+1];
}
}
return index+1;
}
}
27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
class Solution {
public int removeElement(int[] nums, int val) {
int index = 0;
for(int i = 0; i < nums.length; i++){
if(nums[i] != val){
nums[index++] = nums[i];
}
}
return index;
}
}
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
class Solution {
public int maxSubArray(int[] nums) {
int sum = 0;
int max = nums[0];
for(int i = 0; i < nums.length; i++){
if(sum > 0){
sum += nums[i];
}
else{
sum = nums[i];
}
if(sum > max){
max = sum;
}
}
return max;
}
}
class Solution {
public int maxSubArray(int[] nums) {
int sum = 0;
int max = Integer.MIN_VALUE;
for(int i=0; i<nums.length; i++){
sum = sum>0 ? sum+nums[i] : nums[i];
max = Math.max(sum,max);
}
return max;
}
}
88. 合并两个有序数组
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中*,*使 nums1 成为一个有序数组。
初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int index = m + n - 1;
int i = m-1;
int j = n - 1;
while(i >= 0 || j >= 0){
if(i >= 0 && j >= 0){
if(nums1[i] > nums2[j]){
nums1[index] = nums1[i];
i--;
}
else{
nums1[index] = nums2[j];
j--;
}
}
else if(i >= 0 && j < 0){
nums1[index] = nums1[i];
i--;
}
else if(i < 0 && j >= 0){
nums1[index] = nums2[j];
j--;
}
index--;
}
}
}
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length <= 1){
return 0;
}
int min = prices[0], max = 0;
for(int i = 1; i < prices.length; i++) {
max = Math.max(max, prices[i] - min);
min = Math.min(min, prices[i]);
}
return max;
}
}
169. 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3]
输出:3
class Solution {
public int majorityElement(int[] nums) {
int count = 0;
int n = nums[0];
for(int i = 0; i < nums.length; i++){
if(nums[i] == n){
count++;
}
else{
count--;
}
n = count == 0 ? nums[i+1] : n;
}
return n;
}
}
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
/*思路:双循环遍历数组,将遍历到的第一个0与遍历到的第一个非0元素交换位置*/
class Solution {
public void moveZeroes(int[] nums) {
for(int i = 0; i < nums.length-1; i++){
if(nums[i] == 0){
for(int j = i+1; j < nums.length; j++){
if(nums[j] != 0){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
break;
}
}
}
}
}
}
/*思路:设置一个index,表示非0数的个数,循环遍历数组,
* 如果不是0,将非0值移动到第index位置,然后index + 1
* 遍历结束之后,index值表示为非0的个数,再次遍历,从index位置后的位置此时都应该为0
*/
public void moveZeroes(int[] nums) {
if (nums == null || nums.length <= 1) {
return;
}
int index = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
nums[index] = nums[i];
index++;
}
}
for (int i = index; i < nums.length; i++) {
nums[i] = 0;
}
}
448. 找到所有数组中消失的数字
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为*O(n)*的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
示例:
输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]
/*思路:遍历数组a,将数组内的值a[i]作为数组a的索引,即a[a[i]]
* 将a[a[i]]指向的值置为负数(若已为负数则不变)
* 当数组遍历完,仍为正的数的位置,说明其没有在遍历中被遍历到,即数组中没有该索引对应的数
*/
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> result = new ArrayList<Integer>();
for(int i = 0; i < nums.length; i++){
if(nums[i] > 0){
nums[nums[i] - 1] = nums[nums[i] - 1] > 0 ? -nums[nums[i] - 1] : nums[nums[i] - 1];
}
else{
nums[-nums[i] - 1] = nums[-nums[i] - 1] > 0 ? -nums[-nums[i] - 1] : nums[-nums[i] - 1];
}
}
for(int j = 0; j < nums.length; j++){
if(nums[j] > 0){
result.add(j+1);
}
}
return result;
}
}
中等题:
238. 除自身以外数组的乘积
给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
示例:
输入: [1,2,3,4]
输出: [24,12,8,6]
/*思路:记录nums[i]左右部分的乘积随后相乘*/
class Solution {
public int[] productExceptSelf(int[] nums) {
int n=nums.length;
int[]res=new int[n];
int left=1;
for(int i=0;i<n;i++){
res[i]=left;
left=left*nums[i];//记录左边的乘积
}
int right=1;
for(int i=n-1;i>=0;i--){
res[i]=res[i]*right;
right=right*nums[i];
}
return res;
}
}
633. 平方数之和
给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 + b2 = c 。
示例 1:
输入:c = 5
输出:true
解释:1 * 1 + 2 * 2 = 5
/*思路:双指针,从0开始,从sqrt(c)开始*/
class Solution {
public boolean judgeSquareSum(int c) {
int i = 0;
int j = (int)Math.sqrt(c);
while(i <= j){
if(i*i + j*j == c){
return true;
}
else if(i*i + j*j < c){
i++;
}
else{
j--;
}
}
return false;
}
}
字符串:
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
/*
* 思路
*/
定义二维数组dp[length][length],如果dp[left][right]为true,则表示字符串从left到right是回文子串,如果dp[left][right]为false,则表示字符串从left到right不是回文子串。
如果dp[left+1][right-1]为true,我们判断s.charAt(left)和s.charAt(right)是否相等,如果相等,那么dp[left][right]肯定也是回文子串,否则dp[left][right]一定不是回文子串。
所以我们可以找出递推公式
1
dp[left][right]=s.charAt(left)==s.charAt(right)&&dp[left+1][right-1]
有了递推公式,还要确定边界条件:
如果s.charAt(left)!=s.charAt(right),那么字符串从left到right是不可能构成子串的,直接跳过即可。
如果s.charAt(left)==s.charAt(right),字符串从left到right能不能构成回文子串还需要进一步判断
如果left==right,也就是说只有一个字符,我们认为他是回文子串。即dp[left][right]=true(left==right)
如果right-left<=2,类似于"aa",或者"aba",我们认为他是回文子串。即dp[left][right]=true(right-left<=2)
如果right-left>2,我们只需要判断dp[left+1][right-1]是否是回文子串,才能确定dp[left][right]是否为true还是false。即dp[left][right]=dp[left+1][right-1]
class Solution {
public String longestPalindrome(String s) {
if(s.length() < 2){
return s;
}
boolean[][] dp = new boolean[s.length()][s.length()];
int maxLen = 0;
int left = 0;
int right = 0;
for(int i = 1; i < s.length(); i++){
for(int j = 0; j < i; j++){
if(s.charAt(i) == s.charAt(j)){
if(i == j){
dp[j][i] = true;
}
else if(i - j <= 2){
dp[j][i] = true;
}
else{
dp[j][i] =dp[j+1][i-1];
}
}
if(dp[j][i] && i-j+1 > maxLen){
maxLen = i-j+1;
left = j;
right = i;
}
}
}
return s.substring(left,right+1);
}
}
13. 罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I可以放在V(5) 和X(10) 的左边,来表示 4 和 9。X可以放在L(50) 和C(100) 的左边,来表示 40 和 90。C可以放在D(500) 和M(1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
/**
*思路:使用Map来存储对应的值,然后就是简单的计算
*/
class Solution {
public int romanToInt(String s) {
Map<Character, Integer> map = new HashMap<>();
map.put('I',1);
map.put('V',5);
map.put('X',10);
map.put('L',50);
map.put('C',100);
map.put('D',500);
map.put('M',1000);
int flag = 0;
for (int i=0; i<s.length()-1; i++){
if(map.get(s.charAt(i)) < map.get(s.charAt(i+1))){
flag -= map.get(s.charAt(i));
}else {
flag += map.get(s.charAt(i));
}
}
flag += map.get(s.charAt(s.length()-1));
return flag;
}
}
20. 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
示例 4:
输入:s = "([)]"
输出:false
示例 5:
输入:s = "{[]}"
输出:true
/**
* 使用栈先进后出的特点
*/
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i=0; i<s.length(); i++){
if(s.charAt(i) == '('){
stack.push(')');
}
else if(s.charAt(i) == '['){
stack.push(']');
}
else if(s.charAt(i) == '{'){
stack.push('}');
}
else if(stack.isEmpty() || s.charAt(i) != stack.pop()){
return false;
}
}
return stack.isEmpty();
}
}
28. 实现 strStr()
实现 strStr() 函数。
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。
示例 1:
输入:haystack = "hello", needle = "ll"
输出:2
示例 2:
输入:haystack = "aaaaa", needle = "bba"
输出:-1
示例 3:
输入:haystack = "", needle = ""
输出:0
class Solution {
public int strStr(String haystack, String needle) {
if(haystack.equals(needle)){
return 0;
}
int len = needle.length();
for(int i = 0; i <= haystack.length()-len; i++){
if(haystack.substring(i,i+len).equals(needle)){
return i;
}
}
return -1;
}
}
1021. 删除最外层的括号
有效括号字符串为空 ("")、"(" + A + ")" 或 A + B,其中 A 和 B 都是有效的括号字符串,+ 代表字符串的连接。例如,"","()","(())()" 和 "(()(()))" 都是有效的括号字符串。
如果有效字符串 S 非空,且不存在将其拆分为 S = A+B 的方法,我们称其为原语(primitive),其中 A 和 B 都是非空有效括号字符串。
给出一个非空有效字符串 S,考虑将其进行原语化分解,使得:S = P_1 + P_2 + ... + P_k,其中 P_i 是有效括号字符串原语。
对 S 进行原语化分解,删除分解中每个原语字符串的最外层括号,返回 S 。
示例 1:
输入:"(()())(())"
输出:"()()()"
解释:
输入字符串为 "(()())(())",原语化分解得到 "(()())" + "(())",
删除每个部分中的最外层括号后得到 "()()" + "()" = "()()()"。
示例 2:
输入:"(()())(())(()(()))"
输出:"()()()()(())"
解释:
输入字符串为 "(()())(())(()(()))",原语化分解得到 "(()())" + "(())" + "(()(()))",
删除每个部分中的最外层括号后得到 "()()" + "()" + "()(())" = "()()()()(())"。
/**
* 思路:因为括号"()",左右对称,遍历字符串
* 通过变量count统计"("个数,当遍历到")"时,count--
* count==0时,可以得到一个完整的有效的括号字符串。
* 遍历至字符串结束
*/
class Solution {
public String removeOuterParentheses(String S) {
int count = 0;
int index = 1;
String res = "";
for(int i = 0; i < S.length(); i++){
if(S.substring(i,i+1).equals("(")){
count++;
}else{
count--;
}
if(count == 0){
res += S.substring(index,i);
index = i+2;
}
}
return res;
}
}
208. 实现 Trie (前缀树)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
/**
* 用HashMap存完整字符串和部分字符串
* 用List存完整字符串
* 如果HashMap找不到,就遍历List找
*/
class Trie {
/** Initialize your data structure here. */
public Trie() {
}
HashMap<String, String> map = new HashMap<>();
List<String> list = new ArrayList<>();
/** Inserts a word into the trie. */
public void insert(String word) {
if(word.length() > 3){
map.put(word,word.substring(0,3));
}
else{
map.put(word,word.substring(0,word.length()));
}
list.add(word);
}
/** Returns if the word is in the trie. */
public boolean search(String word) {
if(map.containsKey(word)){
return true;
}
return false;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
public boolean startsWith(String prefix) {
if(map.containsValue(prefix)){
return true;
}
else{
for(int i = 0; i < list.size(); i++){
if(prefix.length()<=list.get(i).length()){
if(list.get(i).substring(0,prefix.length()).equals(prefix))
return true;
}
}
}
return false;
}
}
/**
* Your Trie object will be instantiated and called as such:
* Trie obj = new Trie();
* obj.insert(word);
* boolean param_2 = obj.search(word);
* boolean param_3 = obj.startsWith(prefix);
*/
451. 根据字符出现频率排序
给定一个字符串,请将字符串里的字符按照出现的频率降序排列。
示例 1:
输入:
"tree"
输出:
"eert"
解释:
'e'出现两次,'r'和't'都只出现一次。
因此'e'必须出现在'r'和't'之前。此外,"eetr"也是一个有效的答案。
/**
*思路:
*遍历字符串,利用哈希表存储元素key为元素,value为出现次数
*颓废代码
*/
class Solution {
public String frequencySort(String s) {
String res = "";
Map<Character, String> map = new HashMap<>();
for(int i = 0; i < s.length(); i++){
if(map.containsKey(s.charAt(i))){
map.replace(s.charAt(i), map.get(s.charAt(i)) + s.charAt(i));
}else {
map.put(s.charAt(i), ""+s.charAt(i));
}
}
String[] strings = new String[map.size()];
int k = 0;
for (String value : map.values()){
strings[k] = value;
k++;
}
for (int j = 0; j < map.size(); j++){
for (int i = 0; i < map.size()-1; i++){
if (strings[i].length() > strings[i+1].length()){
String temp = strings[i];
strings[i] = strings[i+1];
strings[i+1] = temp;
}
}
}
for (int i = 0; i < map.size(); i++){
res = strings[i] + res;
}
return res;
}
}
二叉树:
671. 二叉树中第二小的节点
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或 0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的**第二小的值。**如果第二小的值不存在的话,输出 -1 。
示例 1:
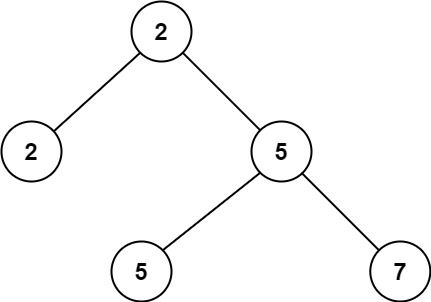
输入:root = [2,2,5,null,null,5,7]
输出:5
解释:最小的值是 2 ,第二小的值是 5 。
示例 2:
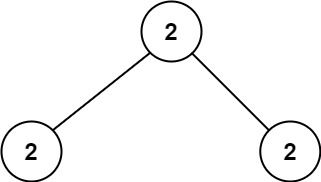
输入:root = [2,2,2]
输出:-1
解释:最小的值是 2, 但是不存在第二小的值。
/**
* 问题可以转化为求左右子树的最小值,如果左右子树最小值都大于根节点的值取较小的值。
* 其他情况取左右子树较大的值。
*/
class Solution {
List<Integer> list = new ArrayList<>();
public int findSecondMinimumValue(TreeNode root) {
return DLR(root, root.val);
}
public int DLR(TreeNode root, int val){
if(root == null){
return -1;
}
if(root.val > val){
return root.val;
}
int left = DLR(root.left, val);
int right = DLR(root.right, val);
if(left > val && right > val){
return Math.min(left,right);
}
return Math.max(left, right);
}
}
938. 二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
示例 1:
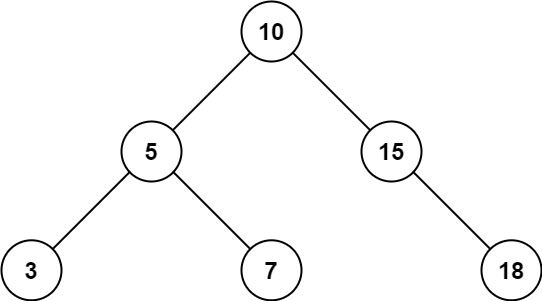
输入:root = [10,5,15,3,7,null,18], low = 7, high = 15
输出:32
示例 2:
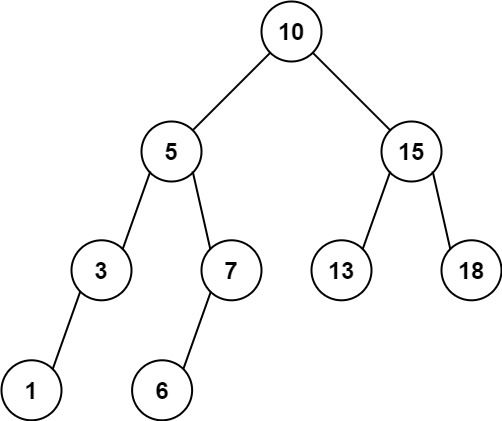
输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出:23
/**思路:中序遍历即可
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
ArrayList<Integer> list = new ArrayList<>();
int res = 0;
public int rangeSumBST(TreeNode root, int low, int high) {
LDR(root,low,high);
return res;
}
public void LDR(TreeNode root, int low, int high){
if(root == null){
return;
}
LDR(root.left,low,high);
if(root.val >= low && root.val <= high){
res +=root.val;
}
LDR(root.right,low,high);
}
}