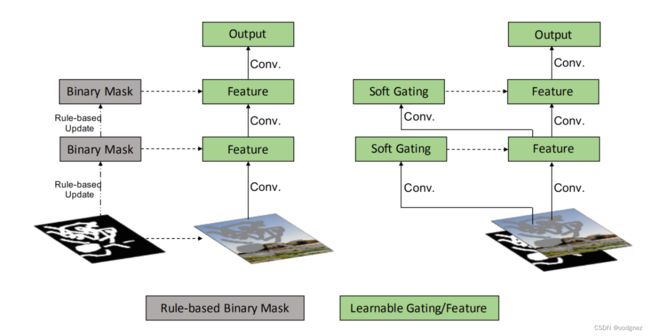
Partial convolution && Gated convolution
组会讨论帖
1. 图像修复
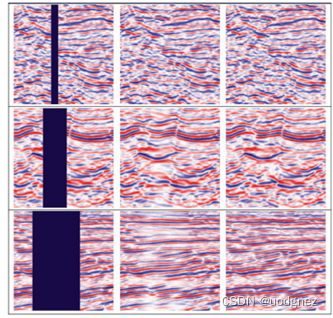
图像修复(inpainting),顾名思义,就是将图像中损坏的部分修复起来,是一种图像编辑技术,可以应用在移除物体、修复老照片、图像补全(eg,地震插值)等等。
2. Partial convolution
论文链接:Image Inpainting for Irregular Holes Using Partial Convolutions (2018 ECCV)
在这之前的深度学习图像补全方法都是使用普通的端到端CNN来做,即把损坏的图像作为输入,完整图像作为标签来进行学习。而普通的卷积(vanilla convolution)作用在图像的损坏区域时,大多数计算都被浪费掉了,因为损坏区域的像素点为0或者1;同时,卷积核在做运算时不能区别损坏和未损坏的区域,对两部分的信息差并不敏感。
Pconv通过加入mask掩码参与到卷积运算中,大大提升了运算效率,且将损坏与未损坏区域的像素区分开来,提升了其敏感性。
为什么传统卷积不适应于图像修复[free-form]任务问题?
传统卷积是将每一个像素都当成有效值去计算的,这个特性使用于分类和检测任务。在这些任务中,输入图像中的所有像素都是有效的,然后普通卷积以滑动窗口方式来提取局部特征。但对于inpainting任务,修复的图像中会存在一些孔洞(即里面的像素是无效的),需要对里面及外面的内容加以区分。
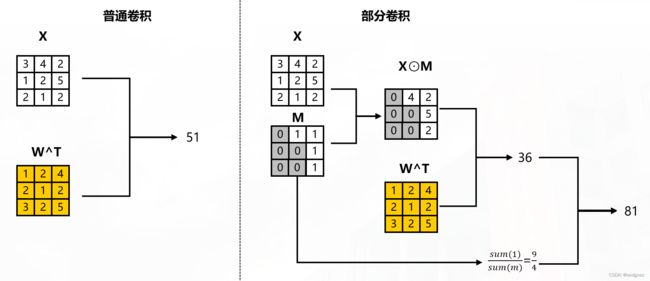
Partial convolutional layer:
x ′ = { W T ( X ⊙ M ) sum ( 1 ) sum ( M ) + b , if sum ( M ) > 0 0 , otherwise x' = \begin{cases} \mathbf{W}^{T}(\mathbf{X} \odot \mathbf{M}) \frac{\text{sum}(\mathbf{1})}{\text{sum}(\mathbf{M})} + b, & \text{if sum} (\mathbf{M}) >0 \\ 0, & \text{otherwise} \\ \end{cases} x′={WT(X⊙M)sum(M)sum(1)+b,0,if sum(M)>0otherwise
其中 X \mathbf{X} X为当前卷积(滑动)窗口的特征值(像素值), M \mathbf{M} M是相应的二进制掩码, W W W为卷积核权重, b b b 为偏置, ⊙ \odot ⊙表示逐像素相乘。对于第一层Pconv中的 M \mathbf{M} M,1代表未损坏区域,0代表损坏区域。
如图所示:
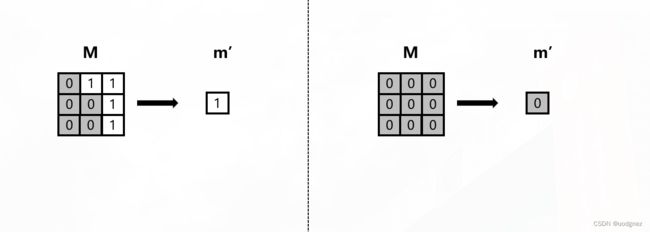
Mask 更新:
m ′ = { 1 , if sum ( M ) > 0 0 , otherwise m' = \begin{cases} 1, & \text{if sum} (\mathbf{M}) >0 \\ 0, & \text{otherwise} \\ \end{cases} m′={1,0,if sum(M)>0otherwise
也就是说, M \mathbf{M} M中只要有一个元素为1,那么更新后的 m ′ m' m′就为1;反之为0。如图所示:
2.1 Loss
带有孔洞的图像为 I i n \mathbf{I}_{in} Iin,初始二进制掩码为 M \mathbf{M} M,网络预测为 I o u t \mathbf{I}_{out} Iout,真实图像为 I g t \mathbf{I}_{gt} Igt。
Per-pixel losses(像素损失):
L h o l e = 1 N I g t ∥ ( 1 − M ) ⊙ ( I o u t − I g t ) ∥ 1 \mathcal{L}_{hole}=\frac{1}{N_{\mathbf{I}_{gt}}} \lVert (1-M)\odot (\mathbf{I}_{out} - \mathbf{I}_{gt}) \rVert_1 Lhole=NIgt1∥(1−M)⊙(Iout−Igt)∥1
L v a l i d = 1 N I g t ∥ ( M ⊙ ( I o u t − I g t ) ∥ 1 \mathcal{L}_{valid}=\frac{1}{N_{\mathbf{I}_{gt}}} \lVert (M \odot(\mathbf{I}_{out} - \mathbf{I}_{gt})\rVert_1 Lvalid=NIgt1∥(M⊙(Iout−Igt)∥1
I c o m p \mathbf{I}_{comp} Icomp代表的是原始输出 I o u t \mathbf{I}_{out} Iout但非孔洞像素设置为ground truth的图像.
Ψ p I ∗ \Psi^{\mathbf{I^*}}_p ΨpI∗表示的是图像 I ∗ \mathbf{I^*} I∗的第 p p p层激活映射(使用ImageNet预训练的VGG-16投影到更高级别的特征空间)
Perceptual loss(感知损失):
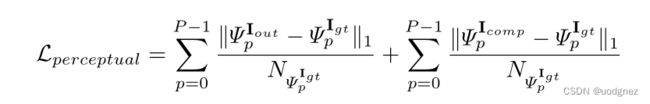
假设高级特征 Ψ p I ∗ \Psi^{\mathbf{I^*}}_p ΨpI∗的形状为 H p W p × C p H_p W_p \times C_p HpWp×Cp,可以得到一个 C p × C p C_p \times C_p Cp×Cp的Gram矩阵, K p K_p Kp为第 p p p层的归一化因子 ( 1 C p H p W p \frac{1}{C_p H_p W_p} CpHpWp1)。
Sytle-loss term(风格损失项):
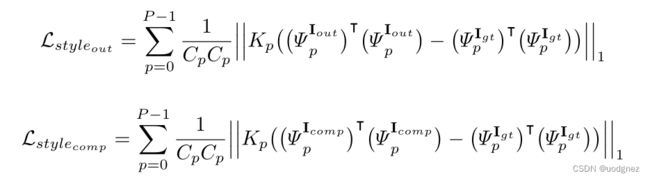
Total variation loss(全变差损失):
L t v = ∑ ( i , j ) ∈ R , ( i , j + 1 ) ∈ R ∥ I c o m p i , j + 1 − I c o m p i , j ∥ 1 N I c o m p + ∑ ( i , j ) ∈ R , ( i + 1 , j ) ∈ R ∥ I c o m p i + 1 , j − I c o m p i , j ∥ 1 N I c o m p \mathcal{L}_{tv} = \sum_{(i,j)\in R,(i,j+1)\in R} \frac{\lVert \mathbf{I}_{comp}^{i, j+1} - \mathbf{I}_{comp}^{i, j} \rVert_1}{N_{\mathbf{I}_{comp}}} + \sum_{(i,j)\in R,(i+1,j)\in R} \frac{\lVert \mathbf{I}_{comp}^{i+1, j} - \mathbf{I}_{comp}^{i, j} \rVert_1}{N_{\mathbf{I}_{comp}}} Ltv=(i,j)∈R,(i,j+1)∈R∑NIcomp∥Icompi,j+1−Icompi,j∥1+(i,j)∈R,(i+1,j)∈R∑NIcomp∥Icompi+1,j−Icompi,j∥1
总损失:
L t o t a l = L v a l i d + 6 L h o l e + 0.05 L p e r c e p t u a l + 120 ( L s t y l e o u t + L s t y l e c o m p ) + 0.1 L t v \mathcal{L}_{total}=\mathcal{L}_{valid} + 6\mathcal{L}_{hole}+0.05\mathcal{L}_{perceptual}+120(\mathcal{L}_{style_{out}}+\mathcal{L}_{style_{comp}}) +0.1 \mathcal{L}_{tv} Ltotal=Lvalid+6Lhole+0.05Lperceptual+120(Lstyleout+Lstylecomp)+0.1Ltv
2.2 其在超分辨率任务上的应用

网络的输入是从低分辨率图像,通过偏移像素和插入孔来构建的。具体如下:
令低分辨率图像为 I I I ,大小为 H × W H \times W H×W, 比例因子为 K K K。
令网络输入图像为 I ’ I’ I’,其大小为 ( K ∗ H ) × ( K ∗ W ) 。 (K*H) \times (K*W)。 (K∗H)×(K∗W)。 对于 I I I 中每个像素 ( x , y ) (x,y) (x,y),将其置于 I ′ I' I′中的 ( K ∗ x + ⌊ K / 2 ⌋ , K ∗ y + ⌊ K / 2 ⌋ ) (K*x + \lfloor K/2 \rfloor, K*y +\lfloor K/2 \rfloor) (K∗x+⌊K/2⌋,K∗y+⌊K/2⌋)上,且相应的 M \mathbf{M} M位置上的值为1。
3. Gated convolution
论文链接:Free-Form Image Inpainting with Gated Convolution (ICCV 2019)
部分卷积(partial convolution)存在什么不足之处?
1.更新Mask的时候,它启发式地将空间位置分类为有效和无效。无论前一层的过滤范围覆盖了多少像素,下一层的掩码都将被设置为1(例如,1个有效的像素和9个有效的像素被当作相同的来更新当前的掩码),这样显得不太合理。
2.每个层中的所有通道都共享同一个掩码mask,这限制了灵活性。本质上,部分卷积可以被视为不可学习的单通道特征硬门控。
Gated convolution layer:
G a t i n g y , x = ∑ ∑ W g ⋅ I Gating_{y,x}= \sum \sum W_g \cdot I Gatingy,x=∑∑Wg⋅I
F e a t u r e y , x ∑ ∑ W f ⋅ I Feature_{y,x}\sum \sum W_f \cdot I Featurey,x∑∑Wf⋅I
O y , x = ϕ ( F e a t u r e y , x ) ⊙ σ ( G a t i n g y , x ) O_{y,x}=\phi(Feature_{y,x}) \odot \sigma(Gating{_{y,x}}) Oy,x=ϕ(Featurey,x)⊙σ(Gatingy,x)
其中 W g W_g Wg W f W_f Wf表示相应卷积核权重, I I I为特征图, ϕ \phi ϕ可以是任何激活函数(比如ReLU),而 σ \sigma σ表示sigmold函数。
门控卷积使得网络可以针对每个channel和每个空间位置,学习一种动态特征选择机制。有趣的是,中间门控值的可视化显示,它不仅能根据背景、遮罩、草图来选择特征,还能考虑到某些通道的语义分割。即使在深层,门控卷积也会学习在不同的通道中突出显示mask区域和草图信息,以更好地生成修复结果。
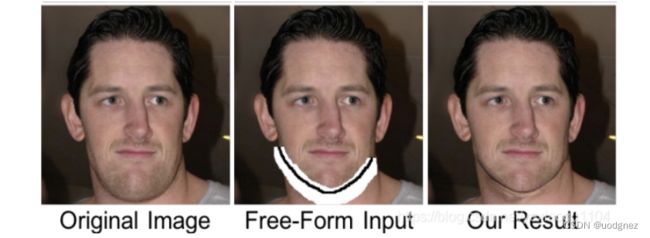
3.1 Loss
生成器:
L G = − E z ∼ P z ( z ) [ D s n ( G ( z ) ) ] \mathcal{L}_{G}=-\mathbb{E}_{z\sim\mathbb{P}_z(z)}[D^{sn}(G(z))] LG=−Ez∼Pz(z)[Dsn(G(z))]
鉴别器:
L D s n = E x ∼ P d a t a ( x ) [ R e L U ( 1 − D s n ( x ) ) ] + E z ∼ P z ( z ) [ R e L U ( 1 + D s n ( G ( z ) ) ) ] \mathcal{L}_{D^{sn}}=\mathbb{E}_{x\sim\mathbb{P}_{data}(x)}[ReLU(\mathbb{1}-D_{sn}(x))]+\mathbb{E}_{z\sim\mathbb{P}_z(z)}[ReLU(\mathbb{1}+D^{sn}(G(z)))] LDsn=Ex∼Pdata(x)[ReLU(1−Dsn(x))]+Ez∼Pz(z)[ReLU(1+Dsn(G(z)))]
3.2 Gconv实现代码
class GatedConv2d(nn.Module):
"""
Gated Convlution layer with activation (default activation:LeakyReLU)
Params: same as conv2d
Input: The feature from last layer "I"
Output:\phi(f(I))*\sigmoid(g(I))
"""
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True,
batch_norm=True, activation=torch.nn.LeakyReLU(0.2, inplace=True)):
super(GatedConv2d, self).__init__()
self.batch_norm = batch_norm
self.activation = activation
self.conv2d = torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, dilation, groups, bias)
self.mask_conv2d = torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride, padding, dilation, groups,
bias)
self.batch_norm2d = torch.nn.BatchNorm2d(out_channels)
self.sigmoid = torch.nn.Sigmoid()
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight)
def gated(self, mask):
return self.sigmoid(mask)
def forward(self, input):
x = self.conv2d(input)
mask = self.mask_conv2d(input)
if self.activation is not None:
x = self.activation(x) * self.gated(mask)
else:
x = x * self.gated(mask)
if self.batch_norm:
return self.batch_norm2d(x)
else:
return x
门控卷积与注意力机制:
相同点:
1.上下文信息捕捉:两者都旨在通过引入机制来捕捉输入数据的长距离依赖关系和上下文信息,以提升模型对数据的理解能力。
2.自适应性:门控卷积和注意力机制都具备自适应性,可以根据输入数据的不同部分自动学习权重或重要性,以进行加权处理。
不同点:
1.应用领域:门控卷积主要应用于卷积神经网络(CNN)中的图像处理任务,例如图像描述生成。而注意力机制广泛应用于循环神经网络(RNN)和Transformer等模型中,用于处理序列数据、语言建模、机器翻译等任务。
2.机制:门控卷积通过引入门控单元(如更新门和重置门)来调整卷积操作的权重,从而对输入进行加权处理。而注意力机制通过计算注意力权重,根据输入和上下文的关联程度来加权输入的不同部分。
3.局部性:门控卷积更关注输入数据的局部区域,通过卷积操作在局部区域上进行加权处理;而注意力机制更注重全局上下文信息,根据输入与上下文的关系动态调整加权权重。
参考文献:
https://zhuanlan.zhihu.com/p/519446359
https://www.cnblogs.com/wenshinlee/p/12591947.html
https://blog.csdn.net/weixin_43135178/article/details/123229497
https://cloud.tencent.com/developer/article/1759006
https://blog.csdn.net/yexiaogu1104/article/details/88293200?ydreferer=aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzEzNTE3OC9hcnRpY2xlL2RldGFpbHMvMTIzMjI5NDk3